舰艇作战系统校准间隔优化研究
杨利斌,林海华,周志恒
(1.海军航空工程学院 兵器科学与技术系,山东 烟台 264001; 2.中国人民解放军92840部队,山东 青岛 266405)
舰艇作战系统校准间隔优化研究
杨利斌1,林海华2,周志恒2
(1.海军航空工程学院 兵器科学与技术系,山东 烟台 264001; 2.中国人民解放军92840部队,山东 青岛 266405)
校准间隔优化研究是舰艇作战系统动态对准理论的重要组成部分;针对目前作战系统校准间隔确定缺乏理论支撑、历史对准误差数据使用率较低的情况,根据历史对准误差数据的特点,提出了利用EEMD-LSSVM-B的组合预测方法对对准误差数据进行预测,从而确定作战系统的校准间隔的优化方法;首先利用EEMD将对准误差数据分解成若干不同频率的分量,分解后的各分量通过LSSVM进行预测,LSSVM的相关参数由QDE算法优化获得,各预测分量通过BP神经网络进行非线性重构,得到最终的预测结果,最后根据预测值对校准间隔进行优化调整;仿真实例表明,组合预测方法比单独的预测方法具有更高的精度,可以应用于作战系统校准间隔的优化过程。
作战系统;校准间隔;集合经验模态分解;最小二乘支持向量机;量子差分进化;BP神经网络
0 引言
舰艇作战系统是结构复杂的多源输入输出、多源信息融合的大系统,是舰艇的主要作战装备。随着计算机技术和网络技术的不断发展和应用,舰艇作战系统内集成了大量的各类传感器和电子设备,这些设备需要根据装备设计方或制造方提供的校准间隔定期进行对准或标校,以保证其精度。
目前,对校准间隔的研究多数为测量仪器的校准间隔优化,主要可以分成定性方法和定量方法。定性的方法主要包括运行测试法、阶梯形法、图像法和统计学法等[1]。定量的方法,是指利用历史校准误差数据建立合理的预测模型,预测得到下一个或几个校准时刻的误差数据,进而对预测超差的设备提前检定校准。定量的方法又可分为基于统计模型和基于非统计模型的方法[2]。基于统计模型的方法需要大量的历史数据,且历史数据必须服从正态分布等[3],实际校准过程中,校准数据很难满足统计模型。基于非统计模型的校准间隔优化方法就是针对测量仪器历史校准数据小样本、非线性的特点,运用非统计的方法对历史校准数据进行建模仿真,来预测其在短期内的发展趋势,从而根据预测的发展趋势来优化校准间隔。主要方法有灰色预测法[4-6]、支持向量机方法[7]和BP神经网络[8]方法等。上述方法主要基于单一的预测模型,在校准间隔优化算法的研究上,使用组合预测模型可以弥补了单一模型进行预测的片面性,从而可以提高模型的预测精度,受到了广泛的关注[9]。
1 对准误差数据序列分析
舰艇作战系统组成复杂,测试设备众多,使用环境恶劣,使得其误差特性也极其复杂,加之平时对准作业进行得较少,其对准误差数据具有小样本、非平稳、非线性的特征,直接使用灰色预测法或支持向量机方法进行预测效果不好。
对准误差数据可划分为趋势项和随机项两部分,其中趋势项反映了各被检设备由于自身特性和使用因素等引起的确定性变化趋势,而随机项则反映了由于外界的随机因素影响导致的随机波动。根据对准误差数据的预测值来动态优化下一次的校准间隔是目前常用的校准间隔优化方法。如果预测得到的对准误差数据在规定的对准偏差内,表明被检设备性能良好,可以适当延长对准间隔;反之,则说明设备超差,需要适当缩短对准间隔。
2 EEMD-LSSVM-BP组合预测模型
2.1 组合预测模型
本文通过对历史对准误差数据的分析,提出利用基于EEMD-LSSVM-BP组合预测方法对作战误差数据进行预测,使预测结果更加准确,为校准间隔的优化提供数据支撑。首先利用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)将非线性非平稳的历史对准误差数据分解成一系列相对比较平稳的分量序列,通过最小二乘支持向量机(Least Square Support Vector Machine,LSSVM)对分解后的各分量进行预测,利用量子差分进化(Quantan Differential Evolution,QDE)对LSSVM进行相关参数寻优,通过BP神经网络对预测得到的分量进行非线性重构,得到最终的对准误差数据的预测结果。组合预测模型结构图如图1所示。

图1 组合预测模型结构图
2.2 EEMD分解
EEMD是一种基于噪声辅助分析的方法,是对EMD方法的改进,可有效消除EMD的模态混叠现象[10]。EEMD的核心是将随机白噪声加入原始信号中并进行多次EMD分解,将各次得到的相对应阶数的IMF分量进行集合平均,当次数足够多时,白噪声平均的结果将相互抵消,从而有效避免了模态混叠现象。
EEMD具体实施步骤如下:
第1步:在待分解信号序列中加入随机产生的白噪声序列;
第2步:对产生的新信号进行EMD分解,得到各阶IMF分量和余项;
第3步:不断重复上述步骤,并且每次加入不同的随机白噪声序列;
第4步:对得到的相应的IMF分量进行求和后平均,得到最后的各阶IMF分量。
2.3 LSSVM的基本原理
设样本的训练集为{(xi,yi)|i=1,2,…,l},其中xi∈Rn为输入向量(n为空间维数),yi∈R为输出,将输入向量从原空间利用非线性映射φ(·)映射到高维的特征空间,则可构造线性回归函数f(x)=ωT·φ(x)+b,其中ω为特征空间中的权系数向量,b为偏移量。
则LSSVM就是求解下列优化问题:
(1)
约束条件为:
yi=ωT·φ(xi)+b+ξi,i=1,2,…,l
(2)
其中:C为惩罚因子,ξi表示回归函数值与实际值之间的偏差。引入Lagrange函数,则上面的约束优化问题就转化为无约束优化问题,得到下式:
(3)
式中,a={a1,a2,…an}表示Lagrange系数。由最优化理论中的KKT条件:
(4)
可得:
(5)
对式消去ω和ξi,得到如下线性方程组:
(6)
式中,E=[1,…,1]T,a=[a1,…,al],y=[y,…,y]T,I是l×l阶单位阵,Ω是l×l阶矩阵,且Ωij=φ(xi)T·φ(xj)。根据Mercer条件,定义如下核函数:
K(xi,xj)=φ(xi)T·φ(xj)
(7)
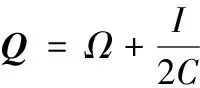
(8)
a=Q-1(y-bE)
(9)
则LSSVM回归函数可表示为:
(10)
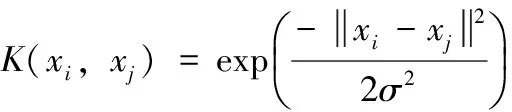
2.4 基于QDE的LSSVM参数优化
由2.3可知,LSSVM模型在建模过程中要确定2个参数:惩罚因子C和核函数参数σ,上述2个参数直接决定了模型的学习水平。
当加载到9%rad(114.57 mm),上角钢加劲肋焊缝裂缝继续增长,且梁上翼缘螺栓松动,且梁腹板屈曲明显,正向峰值荷载停止增加,并且由于作动器牵引绳长度限制,遂停止实验。
QDE算法是一种结合了量子计算与差分进化算法的搜索优化算法[11-12]。为了提高对IMF分量的预测精度,本文采用QDE优化LSSVM相关模型参数,实现参数的自动调整。
优化目标函数定义为:
(11)
s.t.Cmin≤C≤Cmax,σmin≤σ≤σmax
(12)

则基于QDE的LSSVM模型参数的组合寻优具体步骤如下:
第1步:初始化QDE算法的主要参数:种群规模N,染色体长度D,变异因子F,交叉因子C和最大世代数g,其中,g初始数为0。
第2步:产生一个N·D规模均匀分布的随机数矩阵。按照以下方式:
Xi,j=rand·(high[j]-low[j])+low[j]
(13)
其中:i∈{1,2,…,N},j∈{1,2,…,D},high[j]与low[j]分别表示第j列的上界与下界。
第3步:对初始种群进行量子编码。
(14)
其中:r1,r2,r3∈{1,2,…,N}且r1≠r2≠r3,交叉因子C为[0,1]间的随机数。
第5步:交叉操作可以增加种群多样性,该操作按照公式进行。
(15)
式中,j∈{1,2,…,D};D为问题的维数;jrand为{1,2,…,D}中随机选择的一个整数;交叉概率Cr∈[0,1]。
第6步:选择操作保证更优的后代生存到下一世代,选择操作的原则是按照最优适应度进行,适应度的计算按照公式进行。
(16)
第7步:计算结果比较。
若算法达到迭代次数或满足收敛条件,记录最优结果,程序结束,否则返回第2步。
综上,基于QDE的改进LSSVM算法流程图如图2所示。

图2 基于QDE改进的LSSVM算法流程图
2.5 基于BP神经网络的IMF预测分量重构
对准误差数据的预测是一个多因素相关的非线性函数,利用BP神经网络对其进行非线性重构可以取得良好的逼近效果。
利用BP神经网络对预测分量进行非线性重构的步骤如下:
第1步:在经过LSSVM预测后的训练样本取样本(XK,TK),其中K∈{1,2,…,N},N为样本数;
第2步:将输入信息输入到网络中,计算隐层各节点的输出:
(17)
计算输入层节点的输出值:
(18)
第3步:误差修正:对隐层j和节点k的连接权值Wkj和节点k的阀值修正为:
(19)
第4步:通过输出层逆向调整各网络节点的权值;
第5步:依次重复第1~4步,训练结束条件为训练集误差最小化。
3 仿真验证
3.1 测量设备校准间隔优化
本文利用文献[6]中的数据对本文提出的EEMD-LSSVM-BP组合预测方法进行验证。预测数据来源于利用数字万用表E1412A对多产品校准器F5500A进行的每个月一次的监测结果,在标称值为10伏时,要求实际测量不确定度uc小于0.01%,监测结果如表1所示。

表1 校准试验数据
仿真验证时,利用前10个数据进行建模,利用后两个数据进行预测。采用的预测模型分别为基本的GM(1,1)模型,LSSVM模型,EMD-SVM-GM模型[13]和本文的提出的组合预测模型。

当利用BP神经网络进行非线性重构时,BP神经网络结构设置为4-9-1,迭代次数为1 000,学习率为0.5,目标为0.000 04。得到最终的预测结果如图3所示,表2为建模与预测平均相对误差。

图3 各种预测方法比较图

预测方法RMSERMSREGM(1,1)0.03930.0566LSSVM0.03510.0409EMD-SVM-GM0.02200.0229EEMD-LSSVM-BP0.02080.0217
通过图3和表2可知,4种预测方法中,本文所提出的组合预测方法误差最小。GM(1,1)模型预测结果表现为单调的指数序列,对于有波动的序列缺乏应对方法。LSSVM模型的预测性能高于传统的GM(1,1)模型,基于EMD-SVM-GM和EEMD-LSSVM-BP模型的预测精度又高于LSSVM模型,而EEMD-LSSVM-BP的拟合和预测精度均高于其他方法,且性能稳定。
这是因为EEMD可以将非平稳的对准误差数据序列分解为一系列平稳的IMF分量,因此与原数据序列相比,更易于预测。在LSSVM参数寻优时,由于QDE算法采用量子编码方案,增加了对解空间的遍历能力,同时发挥了量子计算的优势,与其他优化算法相比,基于QDE算法的LSSVM参数寻优具有较强的搜索能力与效率。而利用BP神经网络对IMF预测分量进行重构,在可能的减少误差的情况下,可以使得预测模型更平滑。
3.2 某武器系统校准间隔优化
某武器系统为引进自国外的装备,根据武器使用规程,需要每3个月对其距离参数进行一次对准,其距离参数的对准偏差为6 m,历史对准误差数据如表3所示。

表3 距离参数校准数据
首先利用EEMD方法对对准误差数据进行分解,分解结果见图4,包含一个IMF分量和残余分量,IMF分量呈现波动趋势,而残余分量呈递增趋势。对这两部分分别采用LSSVM进行预测,综合两者的预测,得到一步预测结果见图5。

图4 数据的EEMD分解

图5 一步预测结果
利用组合预测模型进行预测时,其建模的误差为0.024 65,建模精度较高;其一步预测的数据为5.485 m,在对准偏差范围内,不需要缩短校准间隔。但是,由EEMD分解得到的趋势项可以看出,对准误差呈增大的趋势,因此在以后的对准过程中要密切关注误差的变化情况。
4 结束语
作战系统对准间隔的优化研究是作战系统动态对准理论的重要组成部分,由于作战系统中各设备的使用环境恶劣,历史对准数据较少,对历史对准数据进行有效利用显得尤为重要。本文在分析历史对准误差数据的基础上,提出了将EEMD、LSSVM和BP神经网络方法组合应用于对准误差数据的预测上,发挥了各自方法的优势,取得了良好的预测效果,为校准间隔的优化提供了数据支撑。
[1] 尧礼辉,张胜宇.计量器具检定、校准周期确定方法的研究[J].计量与测试技术,2010,37(10):63-65.
[2] 孙 群,赵 颖,王国华.测量仪器校准间隔的动态灰色线性回归预测[J].中国测试,2013,39(1):39-42.
[3] 韩 旭,祖先锋,蔡迎波.基于可靠性指标的测试系统校准周期优化[J].航空动力学报,2010,25(7):1640-1645.
[4] 田旭光,蔡金燕.基于灰色预测理论的测量仪器校准周期的确定[J].自动化仪表,2007,28(12):12-15.
[5] 孙 群,赵 颖,孟晓风.基于灰色组合模型的校准间隔优化仿真[J].系统仿真学报,2008,,20 (9):2296-2299.
[6] 赵瑞贤,孟晓风,王国华.基于灰色马尔柯夫预测的测量仪器校准周期动态优化[J].计量学报,2007,28(2):184-187.
[7] 岳瑞华,杨学猛,徐中英.基于粒子群优化支持向量机的测控设备校准间隔预测[J].航天控制,2013,31(2):84-88.
[8] 曹伙俊,赵 芳.基于线性趋势与神经网络的校准间隔组合预测[J].计测技术,2014,34 (3):15-18.
[9] 陈友华.组合预测方法有效性理论及其应用[M].北京:科学出版社,2008.
[10] Zhaohua W, Huang N E.Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009,1(1):1-41.
[11] 马 玲,于 青,刘 刚,等.基于量子差分进化算法的电力系统无功优化[J].电力系统与保护,2013,41(17):39-43.
[12] 孙 薇,刘默涵.基于改进最小二乘支持向量机的短期负荷预测[J].电力科学与工程,2015,31(12):16-21,33.
[13] 姚刚,赵建军,孙靖杰.某武器系统测量设备标校周期优化研究[J].自动化仪表,2014,35(3):28-31.
Research on Calibration Interval Optimization of Warship Combat System
Yang Libin1,Lin Haihua2,Zhou Zhiheng2
(1.Department of Ordnance Science and Technology,Naval Aeronautical Engineering Institute, Yantai 264001,China; 2.Unit 92840 of PLA, Qingdao 266405,China)
Calibration interval optimization is an important component of the dynamic alignment theory of combat system. For the lack of theoretical support of calibration interval determination of combat system and the low usage of historical alignment error data, a calibration interval optimization method utilizing EEMD-LSSVM-BP combination forecasting is proposed according to the characteristic of historical alignment error data in this paper. Firstly the alignment error data is decomposed into several different frequency components by EEMD, which is predicted by LSSVM, parameters of LSSVM are obtained by QDE optimization algorithm, and each prediction component are reconstructed nonlinearly by the BP neural network to give the final prediction, and the calibration interval is adjusted and optimized based on the predicted value at last. The simulation shows that the combination forecasting method has higher accuracy than the individual prediction method, and can be applied to the calibration interval optimization process.
combat system;calibration interval;ensemble empirical mode decomposition; least square support vector machine; quantum differential evolution;BP neural network
2016-05-30;
2016-07-15。
杨利斌(1978-),男,山西清徐人,教员,主要从事武器系统标校方向的研究。
1671-4598(2016)12-0096-04
10.16526/j.cnki.11-4762/tp.2016.12.027
TP274
A

