一种基于空间方位角的投影瞄准算法

王灵艳，李 智，牛军浩，马光利

（1.桂林电子科技大学电子工程与自动化学院，广西桂林 541004；2.桂林航天工业学院电子信息与自动化学院，广西桂林 541004；3.桂林电子科技大学广西自动检测技术与仪器重点实验室，广西桂林 541004）

一种基于空间方位角的投影瞄准算法

王灵艳1，李 智2，牛军浩3，马光利1

（1.桂林电子科技大学电子工程与自动化学院，广西桂林 541004；2.桂林航天工业学院电子信息与自动化学院，广西桂林 541004；3.桂林电子科技大学广西自动检测技术与仪器重点实验室，广西桂林 541004）

针对虚拟瞄准训练系统中真实环境的现实瞄准位置与投影场景的虚拟瞄准位置存在偏差的问题，提出了一种基于空间方位角的投影瞄准算法。通过电子罗盘采集投影区域空间方位角信息进行投影平面空间定位并建立空间直角坐标系，然后通过空间直角坐标与像素坐标的转换，消除屏幕投影形变引起的坐标差异，运用运动轨迹分析解决支点转动引起的偏差。实验结果表明，该算法能够实现实际瞄准位置与虚拟瞄准位置的统一，减小因投影形变、支点转动等因素引起的瞄准位置偏差，达到预期的精度要求，保证训练效果。

瞄准训练；电子罗盘；像素坐标；投影形变；瞄准算法

随着科技的发展，计算机虚拟技术日益成熟，各类虚拟现实系统越来越多地应用于日常生活及军事领域。为了提高部队日常训练的现代化水平，节约实弹射击训练所需的高昂成本，研制虚拟瞄准训练系统已成为一种必然趋势。虚拟瞄准训练系统使用投影屏幕投影三维虚拟场景，通过机械瞄准具对投影场景中的虚拟飞行目标进行瞄准发射训练。若系统判定的虚拟瞄准位置与实际瞄准位置不一致，即实际操作时已瞄准飞行目标的投影点，但系统认定虚拟场景中的飞行目标未被瞄准，此时训练系统将失去瞄准功能，不能进行瞄准训练。因此，虚拟与现实中的瞄准差异将直接影响系统的训练功能和训练效果。文献［1］提出了外加摄像机的方法，拾取激光在平面的投射图像，经图像分析处理确定投射点位置。此方法激光投射点的识别依赖于一些特定的条件：1）要求屏幕对摄像机完全可见；2）系统启动后，屏幕与摄像机之间无相对运动；3）投射的激光点必须比屏幕上的其他部分更亮，包括投影的各种变化图像。而实际瞄准训练中不允许激光辅助，一旦进行实际训练，该方法将失去意义。

鉴于此，提出了一种基于空间方位角的投影瞄准算法。通过电子罗盘采集并记录投影画面上已标定的校准点的方向角和俯仰角信息，定位投影平面空间位置，再将现实中瞄准目标点时该点的空间坐标和虚拟场景中被瞄准目标的虚拟空间坐标统一换算到像素坐标系进行对比、误差修正，使实际瞄准位置与虚拟瞄准位置一致，实现瞄准效果。

1 瞄准训练系统

瞄准训练系统主要由主控计算机、投影屏幕和瞄准装置3个部分组成，如图1所示。在主控计算机设置当前虚拟训练场景，并将场景及校正所需的校准点在大屏幕上进行投影［2-4］。训练人员在指挥员指挥下操作瞄准装置完成校正及相关训练操作，其各项操作参数通过装置中的无线通信模块传输到主控计算机，用于相关计算及判定。

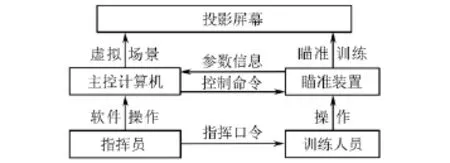
图1 虚拟瞄准训练系统Fig.1 Virtual training system

电子罗盘位于瞄准装置中，方向角以正北方向为0°、顺时针为正方向进行测量；俯仰角以水平方向为0°、上仰方向为正方向进行测量。电子罗盘根据瞄准装置的姿态实时采集俯仰角和方向角信息，并通过无线方式传输给主控计算机。可通过瞄准装置上的机械瞄准具瞄准校准点，也可通过瞄准装置上的辅助瞄准激光完成。瞄准校准点后扣下扳机，主控计算机依据扳机扣下的开关信号判断此时电子罗盘传输的数据是否为校准点的角度信息。各校准点信息采集完毕即可通过投影瞄准算法实现瞄准功能。

通过定位投影平面与瞄准装置的相对位置建立虚拟场景与现实瞄准之间的联系。瞄准装置依次瞄准投影屏幕上的校准点Q、T、D、K、E，采集投影屏幕空间方位角信息，虚拟瞄准训练场景如图2所示。系统根据该角度信息进行投影瞄准算法计算，实现瞄准功能。此时训练人员才可用瞄准装置瞄准跟踪屏幕上的虚拟飞行目标进行瞄准发射训练。通过投影瞄准算法，系统根据电子罗盘传输的角度信息对瞄准装置跟踪瞄准虚拟飞行目标的过程进行判定，再结合瞄准装置的各项操作参数完成虚拟场景中导弹发射、导弹飞行轨迹、能否击中目标等判定。

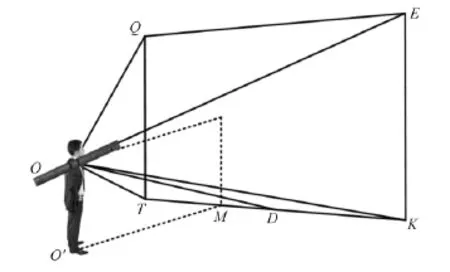
图2 虚拟瞄准训练场景Fig.2 Virtual training scene

2 投影瞄准算法的实现

投影瞄准算法的目的是使虚拟瞄准位置与现实瞄准位置一致，实现瞄准功能，使虚拟瞄准训练系统能进行正常、有效的训练［5］。

2.1 投影瞄准算法原理分析

投影瞄准算法通过校准点对投影平面进行定位，确定瞄准装置与投影场景的相对位置；通过投影画面各顶点位置确定投影形变情况，再利用直角坐标和像素坐标的转换消除该形变产生的瞄准误差；最后消除支点转动引起的偏差，完成虚拟与现实瞄准的统一。

系统通过瞄准具瞄准校准点采集其方向角及俯仰角信息，用瞄准装置上的辅助瞄准激光进行瞄准，以减小测量误差。通过OpenGL函数可在投影画面相应像素坐标点画出校准点，如图2的校准点为Q、T、D、K、E。由瞄准装置支点O分别瞄向屏幕投影的4个顶点Q、T、K、E及底边中点D。4个顶点可确定一个锥形空间区域，不能确定屏幕所在平面位置，再加上点D可确定一系列平行且相似于四边形QTKE的四边形组。再以底边TK的长度作为限制条件，可确定唯一投影屏幕相对于瞄准装置的位置。

虚拟训练系统共包含虚拟场景空间直角坐标系、屏幕投影画面中的像素坐标系、现实中的空间直角坐标系3个坐标系。虚拟空间坐标系与现实空间坐标系均与像素坐标系存在联系。虚拟场景在大屏幕上进行投影时，场景中各点均有相对应的像素坐标；而现实中瞄准装置是以投影的目标像素点为参考点进行瞄准的。因此，现实瞄准位置与虚拟瞄准位置的统一，可利用像素坐标作为中间变量进行转换。

该训练系统虚拟场景采用Vega Prime软件设计［6-7］。Vega Prime中的getWorldToScreenMatrix（）函数可将虚拟场景中任意一点的空间坐标转换为该点在屏幕上显示的像素坐标［8-9］。只需将现实瞄准点的空间坐标转换为对应的屏幕像素坐标，系统比较转换前后的像素坐标即可完成瞄准判定。像素坐标系位于投影画面所在平面，因此需要建立该平面上各点直角坐标与其对应像素坐标之间的关系。

2.2 投影平面空间定位及坐标系的建立

依据校准点空间方位角信息进行相关计算。图2中△OTK在水平面上的投影如图3所示。

图3 水平面投影Fig.3 Horizontal plane projection

O′为瞄准装置支点O在水平面的投影点，M为点O′在TK上的投影点，D为TK中点。TK长度已知，通过校准点的角度信息可得到T、D、K的方向角，设∠TO′D＝γ1，∠DO′K＝γ2，计算点O′相对屏幕的位置，即求O′M、TM的长度。

虚拟瞄准训练的空间几何模型如图4所示。M′为O在屏幕上的投影，β0、β1分别为Q、T的俯仰角。根据lON＝lO′T，以及α0、lO′M、x1的值，即可计算竖直方向各直线的长度。以T为原点建立空间直角坐标系T-xyz。在该坐标系下，投影平面上任意一点被瞄准时，根据此时该点方向角和俯仰角信息可求出该点坐标。投影平面即为该空间直角坐标系下的xTy平面，也是像素坐标系所在平面，因此只需将投影各点在平面直角坐标系xTy下的坐标转换为像素坐标。

图4 瞄准训练空间几何模型Fig.4 Space geometry model of aiming training

2.3 投影形变校正及像素坐标转换

投影形变是指投影画面上各点像素坐标与现实空间坐标的偏移。在理想情况下，投影画面为标准矩形，如图5所示，此时像素坐标系与平面直角坐标系是重叠的。投影区域任意一点的像素坐标等于其平面坐标，此时可直接将平面直角坐标作为像素坐标用于虚拟坐标系与现实坐标系。

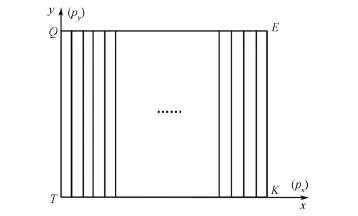
图5 投影矩形Fig.5 Projection rectangle

在现实情况下，由于各类因素，如投影仪摆放位置是否正对投影幕布、投影是否在屏幕中央以及距离远近等影响，投影画面总有一定的形变，使得像素坐标系与平面坐标系产生偏移。这些形变可能是水平方向或竖直方向的梯形形变，甚至可能是二者的叠加。这使得最终投影画面并非标准矩形，而是梯形甚至不规则四边形，投影画面像素坐标系发生形变，各点像素坐标不再等于其平面直角坐标。

投影形变校正就是建立现实平面直角坐标系与变形后像素坐标系之间的对应关系，实现像素坐标转换。在理想情况下，投影画面是如图5所示的矩形，平面直角坐标系xTy和像素坐标系pxTpy是重叠的，可将该矩形区域QTKE看作由无穷多组竖直线段组成，每条竖直直线上各点x坐标相同，px坐标相同，且x＝px。若投影画面产生水平方向梯形形变，如图6所示，则像素坐标系变形，与直角坐标系产生偏移。

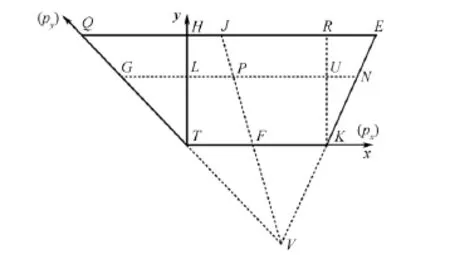
图6 投影画面水平方向梯形形变Fig.6 Trapezoid deformation in horizontal direction of projection

该形变是由像素点的偏移导致的。以分辨率1680像素×1050像素为例，在像素坐标系pxTpy下，T、K、Q、E的像素坐标分别为（0，0）、（1680，0）、（0，1050）、（1680，1050），同时TQ上所有点横向像素坐标均为0，KE上所有点的横向像素坐标均为1680。在直角坐标系xTy下，各点竖直方向直角坐标未发生形变，仍与像素坐标保持一致，但水平方向直角坐标与像素坐标不再一致。

存在该梯形形变时，梯形具有以下几何性质：设V为梯形2条边QT、EK延长线的交点，则任一垂直线段形变后的延长线均过V点。在极端情况下，投影梯形形变为三角形时，底边所有点汇聚为一个点，此时的该点横向像素坐标涵盖了［0，1680］的所有取值。

过V点和投影范围内任一点P的直线FJ与TK、QE分别相交于F、J，则P、F的横向像素坐标相同。GN为过P点且平行于TK的直线，与梯形两腰交点分别为G、N。设像素坐标系下，P点的像素坐标为（px，py），而TK段像素值和GN段像素值同为1680，则像素坐标下存在以下关系：

而在直角坐标系下，△VGN中有

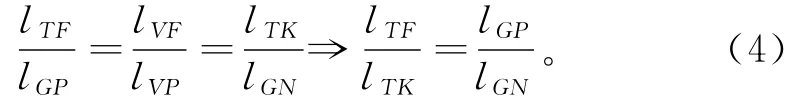
由式（3）、（4）可将形变后各点的直角坐标转换为对应的像素坐标。

已知直角坐标系下，P、Q、E、T、K的直角坐标分别为（xp，yp）、（x1，1050）、（x3，1050）、（0，0）、（1680，0），QE、GP分别与y轴相交于H、L，KR垂直于QE，垂点为R，与GN相交于U，求P点像素坐标（px，py）。在△THQ中有

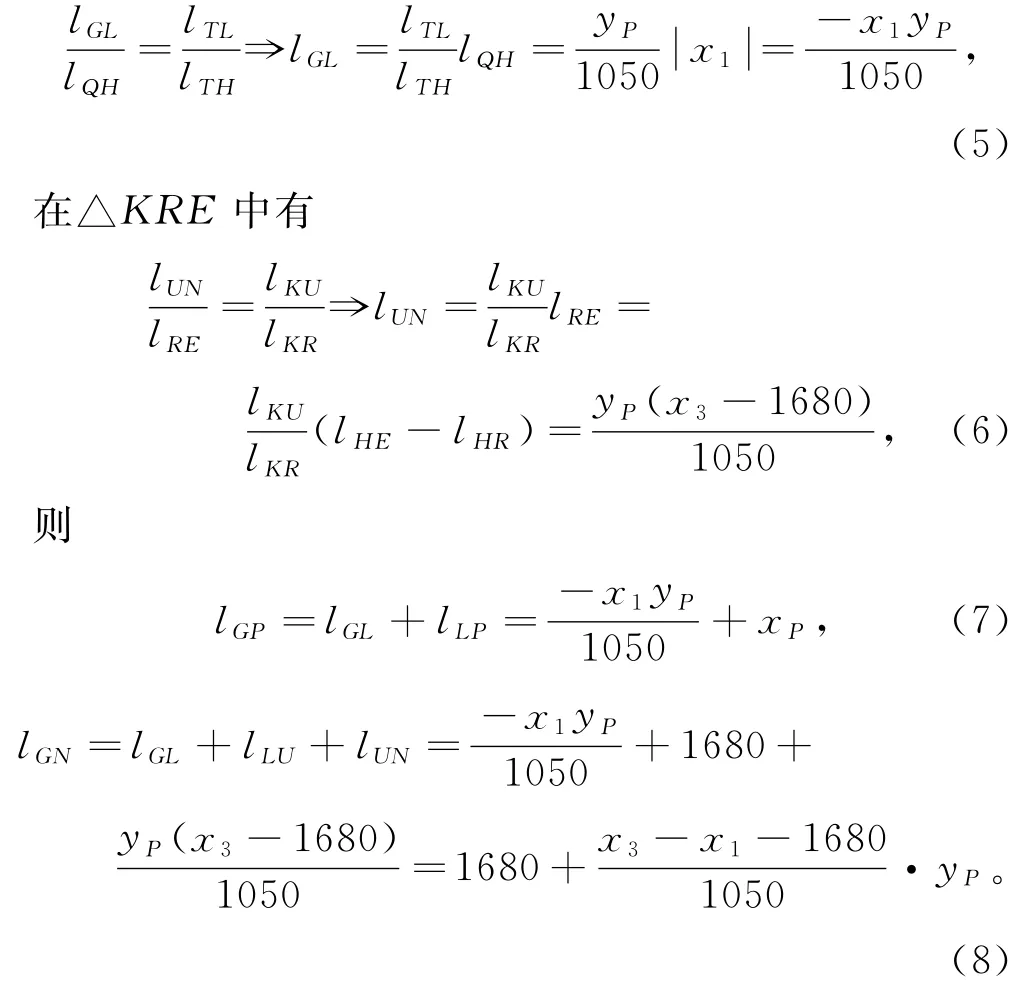
投影画面产生水平方向梯形形变时，竖直方向直角坐标与像素坐标相同，由式（3）、（4）求点P对应的水平方向像素坐标，则有

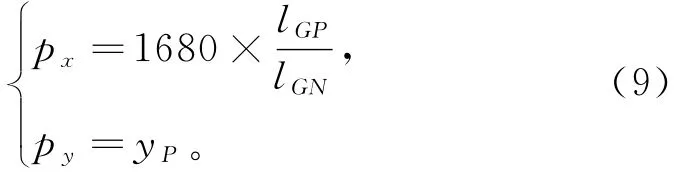
投影竖直方向梯形形变如图7所示，可利用类似原理进行校正。

图7 竖直方向梯形形变Fig.7 Trapezoid deformation in vertical direction

投影形变校正就是将竖直和水平方向的形变进行校正换算后，再次建立直角坐标系与变形的像素坐标系之间的对应关系，将实际瞄准点的平面直角坐标转换为像素坐标。此时虚拟场景中的目标也有对应的像素坐标，将二者进行对比，系统即可判定是否瞄准，从而达到虚拟瞄准与现实瞄准的统一。

2.4 支点转动偏移修正

实际训练中训练装置以人的肩膀为支点进行瞄准，操作人员转动瞄准装置时，支点随之转动。支点转动修正是为了消除该转动带来的影响。

在理想状态下，瞄准装置瞄向N、P、Q和T时，支点O固定不变。而实际操作中支点O会产生位置偏移，水平方向支点偏移如图8所示。瞄准装置瞄准N时，O偏移到O1，产生一个偏角误差，同理向右瞄准P时偏移到O2，发射装置瞄向屏幕任意一点时支点O都会在弧线O1OO2上滑动，因此计算中使用的支点为O3。

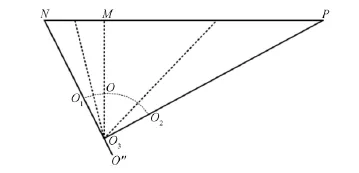
图8 水平方向支点偏移Fig.8 Horizontal pivot offset

支点O水平偏移到O1后测量左侧校准点竖直方向俯仰角时，支点沿弧线上下滑动如图9所示。竖直方向测量的实际支点为O″，且O″在NO1的延长线上。

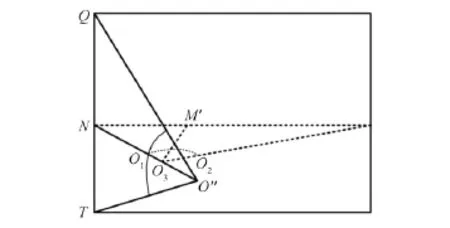
图9 竖直方向支点偏移Fig.9 Vertical pivot offset

O3与O″同在NO1的延长线上，且可能不是同一点，即竖直方向与水平方向在测量过程中使用的可能为不同支点。实际计算是以水平方向为基准，使用支点O3。水平方向的坐标计算不受影响，但在该条件下计算的竖直方向坐标出现偏差，不同支点的竖直方向情况如图10所示，计算所得竖直方向TQ长度实际为被截取的T′Q′长度。

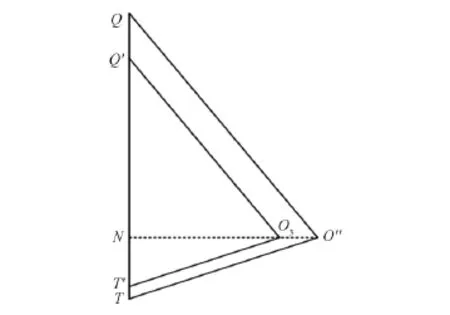
图10 实际支点图Fig.10 Actual pivot

△O3T′Q′相似于△O″TQ，实际所需TQ的长度与T′Q′的长度存在以下比例关系：

竖直方向坐标通过式（10）即可修正支点转动引起的误差。用屏幕分辨率竖直方向像素值作为TQ实际长度进行比例换算，水平方向与竖直方向边长比与实际投影分辨率达到一致。

3 算法验证

投影瞄准算法将瞄准装置瞄准点的实际平面直角坐标和该点对应的虚拟空间坐标统一换算为像素坐标，完成现实瞄准与虚拟瞄准的统一，因此测试点为投影画面上不同像素坐标的点。

用支架支撑瞄准装置进行固定支点测试，排除图8中支点O转动引起的偏差，投影形变校正前测试数据如表1所示。支点不变，投影形变校正后测试数据如表2所示。理论值为测试点的像素坐标，测试值为实际瞄准测试点时平面直角坐标转换的像素坐标。角度误差为由支点分别向理论值点和测试值点发出射线时这两条射线的夹角。从表1可看出，角度误差平均值为1.147°，数据变化规律符合预期，但误差过大。

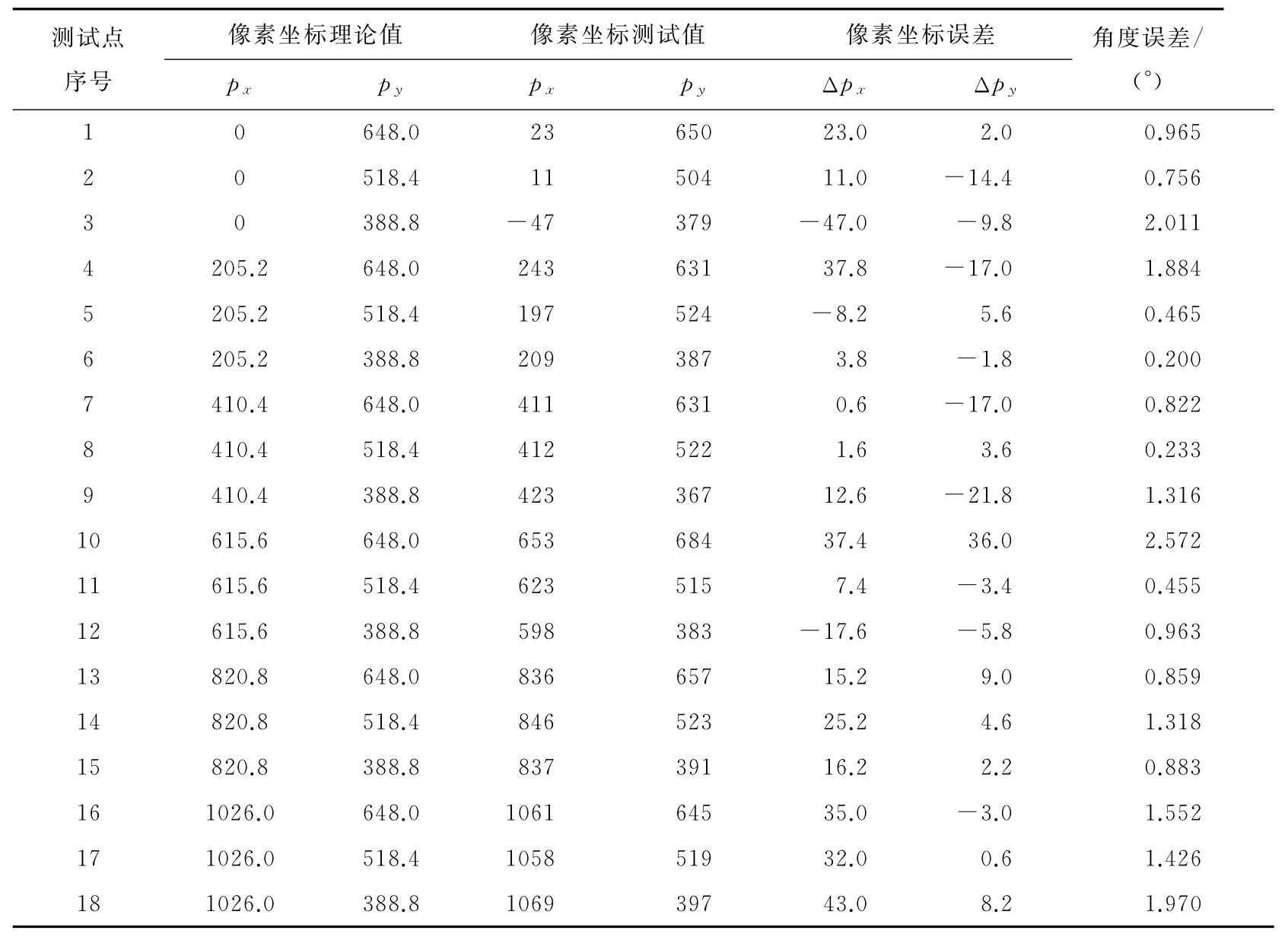
表1 投影形变校正前测试数据Tab.1 The test data before projection distortion is uncorrected

表2 投影形变校正后测试数据Tab.2 The test data after projection distortion is corrected

从表1、2可看出，投影形变校正后角度误差减小，平均值由1.147°降至0.243°，精度显著提升。

以相同的测试点在投影形变校正的前提下，以训练人员的肩膀为支点进行实际训练测试，分别记录支点转动修正前和修正后的测试数据。数据表明，支点转动修正后角度误差减小，平均值由0.876°降至0.227°，精度显著提升。

最后以虚拟飞行目标作为测试瞄准目标进行瞄准发射训练测试，测试结果表明，投影瞄准算法达到了预期目标，可实现瞄准功能，虚拟瞄准位置与现实瞄准位置达到统一，且精度符合预期要求，系统可进行正常瞄准发射训练。

4 结束语

在分析虚拟瞄准位置与现实瞄准位置偏差问题的基础上，提出了一种基于空间方位角的投影瞄准算法。通过电子罗盘测量校准点方位角定位投影平面与瞄准装置相对位置，利用坐标系对应关系进行投影形变校正，通过比例转换进行支点转动修正，最终实现系统的瞄准功能，且瞄准误差在0.5°以内。该瞄准算法不受场地和光线强度等条件的限制，已经成功运用到了虚拟瞄准训练系统中。

［1］ 王全玉，米庆，申鹏洋，等.虚拟发射装置在投影系统中的定位方法研究［J］.系统仿真学报，2012，24（10）：2060-2065.

［2］ 王江春.间瞄火炮室内仿真训练模拟系统研究：迫击炮训练模拟系统［J］.系统仿真学报，2008，20（8）：2018-2022.

［3］ 刘航，王积忠，林峰，等.实验室中基于视景仿真的立体成像与显示技术［J］.实验室研究与探索，2007，26（3）：32-35.

［4］ 郑长伟，卜戍兵，薛青.间瞄火炮射击训练模拟系统的设计与实现［J］.系统仿真学报，2005（9）：2127-2129.

［5］ 董光波，张锡恩.水平度调整和瞄准过程的计算机仿真［J］.计算机仿真，2004，21（7）：26-29.

［6］ 房保国，张大发，林亚军.基于Vega的阀门虚拟仿真技术研究［J］.计算机仿真，2005，22（7）：212-214.

［7］ 薛雪东，徐兵，洪光，等.基于Creator／Vega Prime的某导弹发射设备模拟训练系统［J］.弹箭与制导学报，2008，28（6）：307-310.

［8］ 黄子才，和春耀，胡庭刚.追击炮综合训练模拟系统的设计与实现［J］.指挥控制与仿真，2011，33（4）：95-102.

［9］ 王兰美，赵继成，秦华东.OpenGL及其在VC＋＋下的开发应用［J］.武汉大学学报（工学版），2006，39（4）：62-65.

编辑：张所滨

A projection aiming algorithm based on spatial azimuth

WANG Lingyan1，LI Zhi2，NIU Junhao3，MA Guangli1
（1.School of Electronic Engineering and Automation，Guilin University of Electronic Technology，Guilin 541004，China；2.School of Electronic Information and Automation，Guilin University of Aerospace Technology，Guilin 541004，China；3.Guangxi Key Laboratory of Automatic Detection Technology and Instrument，Guilin University of Electronic Technology，Guilin 541004，China）

In order to solve the problem of the deviation between the actual aiming position in the real environment and the virtual aiming position in the projection scene in virtual aiming training system，aprojection aiming algorithm based on spatial azimuth is proposed.The projection plane space is located and the space rectangular coordinate system is established according to the spatial azimuth information collected by electronic compass.The coordinate difference caused by the screen projection distortion is eliminated through converting the space rectangular coordinate to pixel coordinate.The deviation problem caused by the rotation of the pivot point is solved by analyzing the motion trajectory.Experimental results show that according to the algorithm，the actual aiming position is unified，and the position deviation caused by the projection distortion and the pivot rotation is reduced effectively.The training effect is guaranteed.

aiming training；electronic compass；pixel coordinate；projection deformation；aiming algorithm

TP39

：A

：1673-808X（2016）05-0375-07

2015-12-20

国家自然科学基金（61361006）；广西自动检测技术与仪器重点实验室基金（YQ14203）

李智（1965-），男，广西灵川人，教授，博士，研究方向为自动测试总线与系统、现代测试技术、智能控制。E-mail：cclizhi＠guet.edu.cn

王灵艳，李智，牛军浩，等.一种基于空间方位角的投影瞄准算法［J］.桂林电子科技大学学报，2016，36（5）：375-381.