基于直达客流量的公交路径优化模型及求解算法

齐振涛，李文勇，2，余子威，贺军杰

（1.桂林电子科技大学机电工程学院，广西桂林 541004；2.桂林电子科技大学广西高校智能交通系统重点实验室，广西桂林 541004）

基于直达客流量的公交路径优化模型及求解算法

齐振涛1，李文勇1，2，余子威1，贺军杰1

（1.桂林电子科技大学机电工程学院，广西桂林 541004；2.桂林电子科技大学广西高校智能交通系统重点实验室，广西桂林 541004）

针对已有公交线路优化模型求解过程复杂的问题，从直达客流量的角度对公交最优路径进行求解。采用公交线路必经中间站点的选取方法，将最短路径KSP算法进行改进，用于求解最大直达客流量路径；以最大直达客流量、人均最小成本2个维度为优化目标，建立了基于网络人均出行成本最小的公交线路优化模型，并给出了模型求解的算法。实例证实，公交路径优化模型有效可行，降低了线路求解的难度。

公交线路优化；直达客流量；人均出行成本

随着社会进程加速，公共交通在城市交通中的地位日趋重要，提升公交网络的性能问题已成为科学研究与工程应用中的热点和难点。公交线网的优化需要公交线路路径搜寻理论作为支撑。研究公交路径对整个公交线网的研究和开发有着重要意义。公交最优出行路径的搜索与生成的根本在于网络最优路径模型的建立和算法求解问题。公交路径优化方面的研究国内始于20世纪80年代，文献［1-3］给出了公交路径优化模型及具体求解方法，但均倾向于整个网络，求解计算复杂；于滨等［4］以直达客流密度为目标对王炜等［1］提出的直达量优先的方法作了改进，但并未给出具体求解方法。目前已有的路径寻优算法大部分适用于求解最短路径问题，适合公交路径优化的实用、有效的模型和求解算法研究较少。为此，建立结合实际乘客出行需求的公交路径择优模型，对起终点间的公交出行路径进行优化。该模型将最大直达客流量、最小网络出行成本和可行的路网等因素综合考虑，在保证规划原则的前提下，实现了起终点间的公交路径求解。

1 单条公交线路的优化目标

单条公交线路在优化时应按照以下原则：1）线路的走向服务于主要客流，以满足居民出行的需要；2）尽量提供直达运输，使得乘客总换乘次数最少；3）尽量依照最短距离布设线路，使得所有乘客的总出行时间最小。公交线路的优化属于多目标问题，以上原则在优化时并不能同时满足，为此将模型的主要优化目标设为直达客流量最高和网络中人均出行时间最小。

1.1 可通行公交的道路网

道路网是城市公共交通系统的基础，可通行公交线路的道路必须具备一定的道路条件和交通条件。具体包括：为满足双向安全行车，道路路宽应大于某一值；道路畅通条件好，没有无法排除的交通梗塞；道路长度应满足公交设线的长度要求。

其中G′、G分别为可通行公交线网和城市道路网。

1.2 线路长度约束

公交线路的长度应满足一定条件，线路过长，使得客流分布不均匀，产生运输效率过低和公交线路的非直线系数过大等问题；线路过短，使得公交车辆的调车转向总时间增加，降低了公交车辆的使用效率和公交车的运营车速，同时也增加了乘客的平均换乘次数。

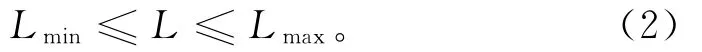
其中：L为公交线路的实际长度；Lmin、Lmax为公交线路允许的最小长度和最大长度。

1.3 线路的非直线约束

公交线路的实际长度与起终点间空间直线距离之比称为线路的非直线系数，记为q，它可以对线路的合理性、快捷性进行评定。公交线路的非直线系数不宜过大，理想值为1，一般取值1.2～1.4。《城市道路交通规划设计规范》明确指出，公共交通线路非直线系数不应大于1.4，

1.4 公交线路首末站点设置

公交首末站的设置一般依据规划区域内高峰小时客流量与途经该区域的所有公交线路的运力对比来确定。当高峰小时客流量大于途经该站点所有公交线路的总运力时，则在该区域设立首末站点，反之则不设立。

其中：Q为公交站点小时最大客流的生成量和吸引量之和；Qmax为公交站点可以承载的小时最大乘客量。

2 优化模型的建立

2.1 公交线路必经中间站点的求解方法

公交线路必经中间站点指线路必须通过的站点，如大型商场、车站等具有明显客流产生量的地点。当线路途经站点和路段较多时，可选线路规模很大，此时不易确定公交线路的走向。若能在求解线路时设定必经中间站点，则只有少数线路是可选的，这样将大大缩小求解范围。为了减小搜索解空间，使求解简化，建立如下寻找必经中间站点的方法［7］。

对于已经确定的居民出行结构，在网络中找到线路起终点的中点位置坐标，将线路中某节点产生的出行量乘以节点到中点的距离，记为fil（x，y），并记线路上所有节点的fil（x，y）之和为。用单节点对应的fil（x，y）除以线路上所有节点的，所求得的值中最小的点即为网络的必经节点。计算方法为：首先建立坐标系，将网络中各个节点位置进行标记。设必经节点的位置为（x，y），l为起点si（si∈S，i＝1，2，…）到终点di（di∈D，i＝1，2，…）的可行线路编号，bil为线路l上第i个节点的总出行量，xi，yi为可行线路l上的节点编号，（xs，ys）为起点的坐标，（xd，yd）为终点的坐标，为中点的坐标，fil（x，y）为第l条可行线路对应的第i个节点到中点坐标距离与bil的乘积。模型如下：

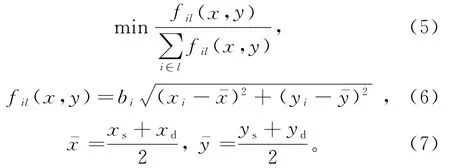
2.2 最大直达客流公交线路模型

依据公交线路的约束准则式（1）～（7），参考文献［4］，简化后的最大直达客流量模型为：

其中：pij为网络内从节点i到节点j的直达乘客量；xij为决策变量，当线路通过路段（i，j）时取值为1，否则取值为0；Zsd为s到d的直达客流量。

2.3 出行成本最小的公交线路优化模型

将城市道路网络简化成一个抽象的无向图问题。设G＝（N，A），其中N为道路节点集，A为弧（边）集，S为起点集，D为终点集，S，D∈N，aij∈A为连接i、j的路段，P为线路所对应的直达客流量矩阵，i，j∈N，构造网络下的任意节点间的出行时间阻抗矩阵T，tij为由i到j所需要的时间。节点间有边连接时为其对应的时间，无边连接时为inf，表示无穷大。U为线路l的人均最小出行消耗时间成本。具体表示为：

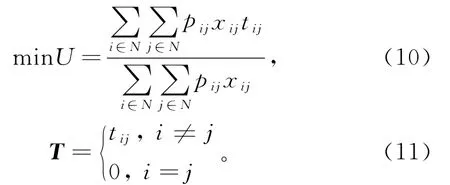
3 模型的算法及求解

3.1 改进的KSP算法

智能搜索算法作为公交线路优化的有力工具，其典型代表是最短路径搜索法。K条最短路径（KSP）算法由Yen［8］于1972年提出，已被广泛用于求解网络中最短路径问题。

公交路径优化其实是路径选择问题，其根本是确定线路途经过的站点和路段。传统KSP算法只能搜索网络中的最短路径，因此需要对KSP算法进行改进（见图1）。具体方法是：将城市道路网络简化为抽象的无向图，分别建立居民出行矩阵M、出行时间阻抗矩阵T。引入一个空矩阵V，先将居民出行矩阵M中的非零项客流数据求导后赋给V。然后将出行时间阻抗矩阵T中值为inf的赋给V，此时得到的矩阵称为过渡矩阵V。用KSP算法对过渡矩阵搜索，搜索的结果就是最大直达量客流的线路。引入过渡矩阵后，最大直达客流的公交线路布设问题转换为在过渡矩阵下的KSP路径求解问题。

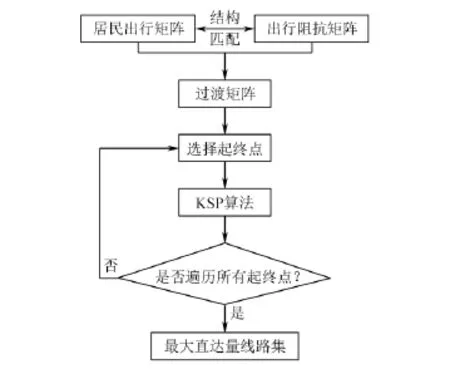
图1 KSP算法改进后求解流程图Fig.1 Flow chart of improved KSP algorithm

3.2 模型求解

结合KSP改进算法，对网络出行成本最小的公交线路模型进行优化求解。依据流程图（见图2），具体步骤为：

1）选择公交起终点，求解线路必经中间站点。

2）在首末站间通过改进的KSP算法搜索最大直达客流量路径，对搜到的路径编号为i。

3）判断第i条路径是否符合约束，若符合，则存入线路集，搜索第i＋1条路径；否则，终止。

4）以网络中人均最小消耗时间成本值最小为目标，在生成的可行线路集中求解。

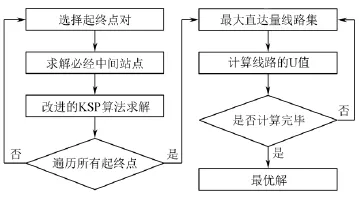
图2 最优线路求解流程图Fig.2 Flow chart of best line optimization

4 算例分析

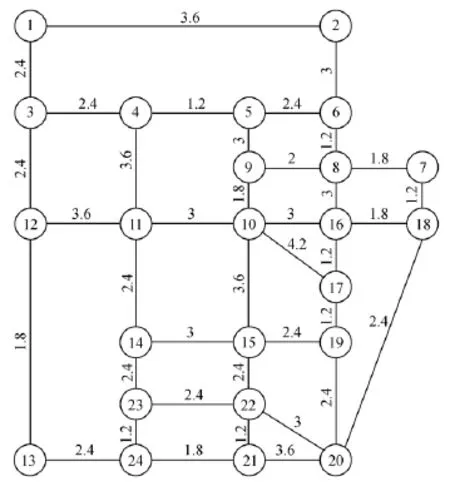
图3 模拟路网Fig.3 Simulation graph of road network

图3为简化的模拟路网。实线表示路段，实线上的数字表示公交车的行驶时间，单位为min，圆圈中数字代表道路节点。已知节点间的乘客出行量，求重新调整节点4到节点22点间的公交线路。由必经节点计算方法可知，节点11为必经节点。

模型求解伪代码：

计算的线路直达客流量及人均出行成本见表1。

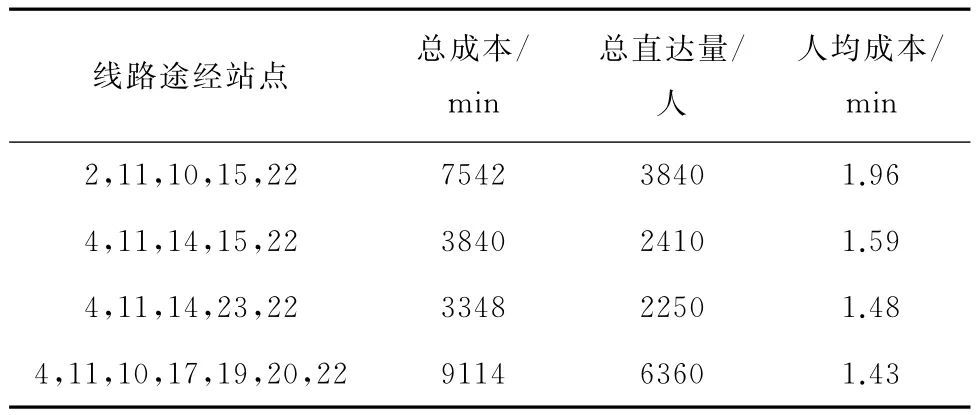
表1 直达客流及人均出行成本Tab.1 Direct passenger flow and per capita travel cost

由传统方法可知，节点4到节点22应该布设的线路为4-11-14-23-22，但从表1可看出，线路4-11-14-23-22实际并不是客流最密集的线路。从总直达客流量和该路网的人均出行成本层面分析，线路4-11-10-17-19-20-22最符合公交布设的原则，因此线路4-11-10-17-19-20-22应优先考虑。

5 结束语

依照公交线路布设的宗旨，建立了直达客流优先的公交线路优化模型，并通过改进的KSP算法，对公交路径进行了优化求解，求解结果验证可行。改进的算法以最大客流走向作为搜索方向，符合公交线路径布设原则。模型实现了求解最大直达客流量最大和网络人均成本最小的公交出行目标。初步考虑直达客流量等主要参数，在站点延误、换乘时间等问题上还有待研究。

［1］ 王炜，陈学武，杨新苗.城市公共交通系统规划方法与管理技术［M］.北京：科学出版社，2002：67-75.

［2］ 陈洪仁，冯树民.分层限制的公交线网优化模型［J］.哈尔滨建筑大学学报，2001，34（5）：113-115.

［3］ 王志栋.公交线网优化模型的建立［J］.大连铁道学院学报，1997，18（4）：33-36.

［4］ 于滨，杨永志，杨忠振，等.基于直达客流密度最大的公交线网优化［J］.哈尔滨工业大学学报，2009.41（2）：205-207.

［5］ 张蕾，PAULO S C.公交线网优化新技术的应用研究［J］.交通标准化，2013，18（21）：15-20.

［6］ 王佳，符卓，杜靖毅.基于遗传算法的城市公交骨架线网优化设计［J］.计算机应用研究，2012，29（12）：4518-4521.

［7］ 武苗苗.城市微循环公交客流特性分析及站点规划方法研究［D］.西安：长安大学，2014：79-82.

［8］ YEN J Y.Finding the lengths of all shortest paths in NNode nonnegative-distance complete networks usingadditions andN3comparisons［J］.Journal of the ACM，1972，19（3）：423-424.

编辑：张所滨

Bus route optimization model and algorithm based on direct passenger flow volume

QI Zhentao1，LI Wenyong1，2，YU Ziwei1，HE Junjie1
（1.School of Mechatronic Engineering，Guilin University of Electronic Technology，Guilin 541004，China；2.Guangxi College Laboratory of Intelligent Transportation System，Guilin University of Electronic Technology，Guilin 541004，China）

In view of the complicated problems in the process of solving the optimization model of bus lines，the optimal path of the bus line is studied in term of direct passenger flow.The study shows that a bus line must pass through node selected model.KSP algorithm is improved for solving the direct flow viable of bus lines.Finally a minimum per capita travel cost bus route optimization model is established based on direct passenger volume and the average per capita minimum cost as the optimization goal.The algorithm for calculating the model is given.The model is verified by apractical example and the model reduces the difficulty of bus line optimization.

bus route optimization；direct passenger flow volume；average travel cost

U491.1

：A

：1673-808X（2016）05-0412-04

2015-12-28

国家自然科学基金（51268006）

李文勇（1976-），男，河南南阳人，教授，博士，研究方向为交通规划与管理、智能交通系统。E-mail：traffic＠guet.edu.cn

齐振涛，李文勇，余子威，等.基于直达客流量的公交路径优化模型及求解算法［J］.桂林电子科技大学学报，2016，36（5）：412-415.