图象在中职学校数学课堂教学中的意义
王丽梅
(大连市轻工业学校)
图象在中职学校数学课堂教学中的意义
王丽梅
(大连市轻工业学校)
职业学校数学课程应注重直观,避免抽象。利用图形解决数学问题,是一个很好的锻炼学生、提升学生、完善学生思维的途径。
中职学校;直观形象;观察
数学课堂,离不开图象。用图象来帮助学生观察、思考、论证,既直观又有效。在此简介图象在数学教学中的作用,以供参考。
作用一:直观
如集合的交并补运算,借助数轴观察要比抽象运算直观、简单得多。具体如:已知集合让学生画数轴进行观察,就简单多了。特别是A∪B的运算,单凭想象,容易产生误解。这样画一个图形:

是不是看起来很直观?交织网状区域为交集范围,单线阴影部分为并集范围。这不仅仅是让学生看到了正确答案,也让学生进一步明确了不等式的含义:即求解的是变量x的取值范围。提高了学生对数学的认知。再如:已知二面角α-l-β的度数为30°,P为平面α内一点,其到棱l的距离为6,求点P到平面β的距离。
正确画图:

这种题目,画图非常重要,要直观、科学。经常加以训练,相信不仅能提高学生的绘图能力,也会在科学地绘制图形的过程中感受到数学的有趣、迷人。
作用二:全面
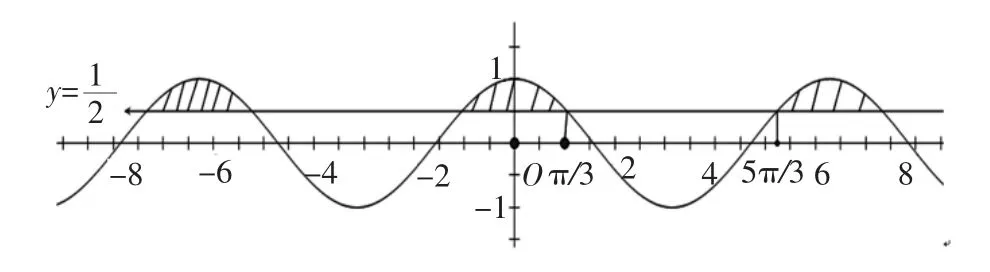
我想,不用教师太多的语言,学生就能看懂、学会并自行总结出求解这类问题应该考虑哪几方面。这就是直观图形的好处。它不仅仅是看起来直观,更能提升学生的总结、归纳能力,一举多得。
作用三:归纳
如学习指数函数,需要通过图象来研究它的性质。无论是利用多媒体手段,还是板书绘图,我们通常会给出下面图象:
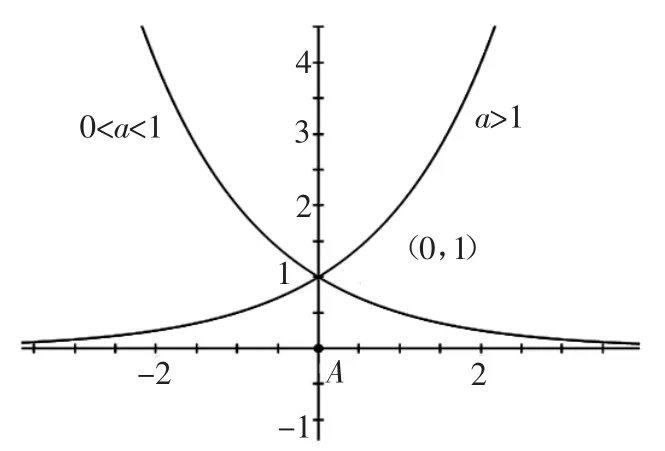
这是讲授指数函数的常规图示。其实,我们还可以进一步归纳如下:
1.a>1,图象随着a值的增大(减小)逐渐靠近(远离)坐标轴。
如图:

2.0 <a<1,图象随着a值的增大(减小)逐渐远离(靠近)坐标轴。如图:
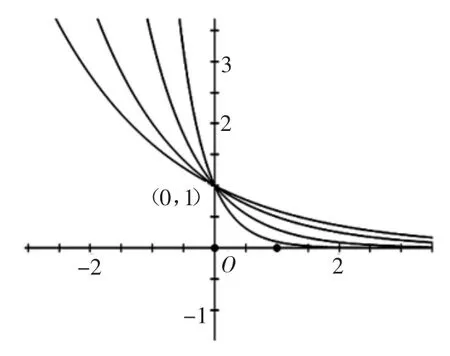
这样做不仅没有增加学生的认知负担,我认为反而更能反映指数函数的特征:增长(减小)的速度非常快。这种特征在日常生活中有很多例证,尤其是对于风险意识的增强提供了理论依据。
作用四:探索、有趣
如学习反函数,如果只是教给学生如何求反函数,完全没有达到我们探究原函数和反函数之间逻辑关系以及学习反函数的意义的目的。如果我们画个图,如下:

学生通过观察,不难发现,以直线y=x为对称轴,两边图形关于直线y=x对称。任取图象上一点p(x,y),其关于直线y=x的对称点坐标为p'(y,x),即变量对调。这就是反函数思想——变量对调。即原来函数的自变量变成因变量,原来函数的因变量变成自变量。这样一来,当我们研究原来函数自变量或因变量性质不方便的时候,也许去研究一下它的反函数的因变量或自变量,就会别有洞天。这就是反函数思想。渗透给学生的不仅仅是一个数学知识,还有思维方法——当一件事情正常渠道处理有困难的时候,不妨换位思考,从另外的角度思考,或许会变得很简单。通过这种学习,培养了学生的探究意识和学习兴趣,也能让学生很直观地看到原函数与反函数之间的关系。
职业学校的数学课程,不一定关注阶段性的数学成绩。我们应该把落脚点放在渗透科学理念、提升数学素养上面。多让学生感受数学的神奇,感受科学的思维方式。利用图形解决数学问题,是一个很好的锻炼学生、提升学生、完善学生思维的途径。愿广大中职学校数学老师能投身到数学教学的研究中来,认真思考,全面提升,真正为提高中职学校学生综合素养做出应有的贡献。
·编辑 李建军
——与非适应性回归分析的比较

