浅谈数列求和的类型及解题方法分析
吴香娥
(山西省汾阳市高级职业中学)
浅谈数列求和的类型及解题方法分析
吴香娥
(山西省汾阳市高级职业中学)
在高中数学教学中,数列求和是一个十分重要的知识点,特别是关于等差和等比数列的求和公式以及推导过程,学生一定要熟练掌握。教师在进行数学教学时,不仅要让学生熟悉数列求和的一般类型和相应的解题方法,还要不断进行总结,并让学生真正领会利用数列求和中所蕴含的数学思想。主要针对高考对数列知识的要求,从几个方面归纳总结数列求和的常用方法。
数列求和;类型;解题方法
在高中代数中,数列求和是其中一个十分重要的内容。数列求和的关键和核心就是对数列的通项公式进行分析,然后对数列的类型予以确定,将其转化为我们所熟知的数列求和的类型。在数列求和中,有几种十分常见的解题方法,在高考中也是常考的对象,数列求和的常用方法有:公式法、倒序相加法、错位相减法、裂项相消法、分组求和法、并项求和法。
一、公式法求和
对等差数列、等比数列,求前n项和Sn可直接用等差、等比数列的前n项和公式进行求解。运用公式求解时应注意:首先要注意公式的应用范围,确定公式适用于这个数列之后,再计算。


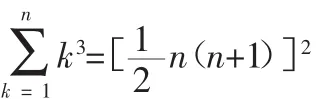
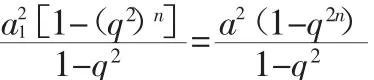
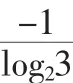
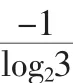
二、倒序相加法求和
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an)
例3.求sin21°+sin22°+sin23°+…+sin288°+sin289°的值。
将①式右边反序得
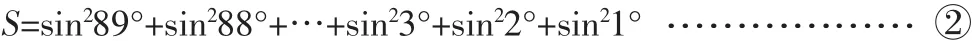
又因为sinx=cos(90°-x),sin2x+cos2x=1,①+②得

∴S=44.5
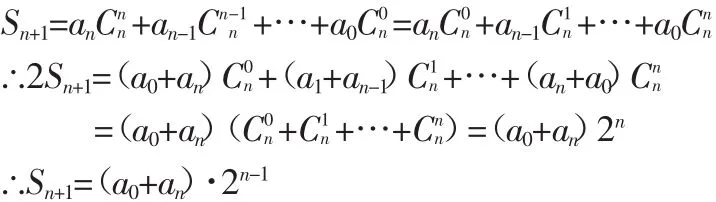
三、错位相减法求和
例6.求和:Sn=1+3x+5x2+7x3+…+(2n-1)xn-1………①
①-②得(1-x)Sn=1+2x+2x2+2x3+2x4+…+2xn-1-(2n-1)xn
四、裂项相消法求和
这是分解与组合思想在数列求和中的具体应用.裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的。
五、分组法求和
有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.
解


六、合并法求和
针对一些特殊的数列,将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和时,可将这些项放在一起先求和,然后再求Sn。
例9.在各项均为正数的等比数列中,若a5a6=9,求log3a1+log3a2+…+log3a10的值。
解:设Sn=log3a1+log3a2+…+log3a10

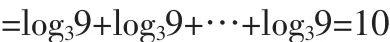
数列求和不仅在高中数学中有着十分重要的作用,也是学习高等数学的基础,有着承前启后的作用。数列求和的方法有很多,要通过平时的积累,更要总结其中所渗透的数学思想方法,将数学思想和方法融为一体,方能在解决数列求和问题时得心应手。本文只总结了几种数列求和的常用方法,还有待于继续研究。
吴琪.浅谈数列求和的类型及解题方法分析[J].数学学习与研究,2014(6).
·编辑 薛直艳
——由倒序相加想到倒序相乘

