三角函数诱导公式和函数的对称性

宋英

（湖北省秭归县秭归二中）

三角函数诱导公式和函数的对称性

宋英

（湖北省秭归县秭归二中）

三角函数的诱导公式我们比较熟悉,但对一些公式所反映的对称性并不熟悉。下面我们来看看函数的对称轴和对称中心吧。

一、轴对称

定理一 如果函数y=f（x）满足f（x+a）=f（x-a）或f（x）=f（2ax），函数y=f（x）的图象关于直线x=a对称。

证明：设函数y=f（x）的图象上的任意一点为P（x，y），点P关于直线x=a的对称点p（2a-x，y），显然有y=f（x）。

说明点p（2a-x，y）也在函数的图象上。

由点P的任意性，说明函数y=f（x）图象关于直线x=a对称。

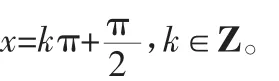
二、中心对称

定理二 如果函数y=f（x）满足y=f（2a-x）=-f（x）或=f（a-x）=-f（a+x）函数y=f（x）的图象关于点（a，0）成中心对称。

证明：设函数y=f（x）的图象上的任意一点为P（x，y），点P关于点（a，0）的对称点p（2a-x，-y）

由f（2a-x）=-f（x），则-y=f（2a-x）

说明点p（2a-x，-y）也在函数y=f（x）的图象上。点P的任意性，说明函数y=f（x）图象关于点（a，0）成中心对称。

应用上述结论就比较容易解决人教版数学必修四教材第70页的第17题：

2.如何根据第1小题并应用正弦函数的性质得出函数y=sinx，的图象？

·编辑 温雪莲