构造斜率求恒成立问题中参数的取值范围

何方璇

（辽宁省大连市经济技术开发区第一中学）

构造斜率求恒成立问题中参数的取值范围

何方璇

（辽宁省大连市经济技术开发区第一中学）

在各省市的高考题中，常将导数作为压轴题的考查对象，而导数中多涉及不等式的恒成立的证明或求解问题，本文以解决不等式恒成立问题的两种方法比较为突破点，发现一类恒成立问题，采用构造动函数分类讨论往往很困难，但若巧妙地构造斜率可以有效地降低题目的思维量和运算量，达到事半功倍的效果。

一、一道高考题的两种解法

【2012全国大纲卷理科第20题】设函数f（x）=ax+cosx，

x∈［0，π］

（1）讨论f（x）的单调性；（2）设f（x）≤1+sinx，求a的取值范围。

解：（1）略

解法1：ax+cosx≤1+sinx，x∈［0，π］等价转换为ax+cosx-1-sinx≤0，

令g（x）=ax+cosx-1-sinx，要使g（x）≤0成立，只需使gmax（x）≤0

gmax（x）=g（π）=aπ-2≤0

②当a≤-1时，g′（x）≤0，g（x）在x∈［0，π］上单调递减，gmax（x）=g（0）=0≤0

即a∈R，所以a≤-1

当x∈［0，x1），g′（x）＞0，g（x）单调递增，因为g（0）=0，∃x3∈［0，x1）使g（x3）≥g（0）=0

解法2：ax+cosx≤1+sinx

①当x=0时，a∈R

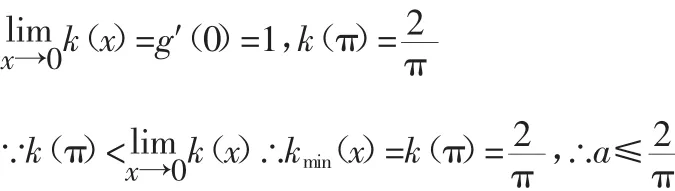
解法1构造含参数的动函数，此法的难点在于就参数a进行分类讨论。若采用分离常数构造定函数利用导数求最值的办法，需要二阶求导和洛必达法则，超出了高中生的理解范围。

解法2采用了分离常数构造割线和切线斜率的办法，有效地规避了分类讨论，也降低了求导的繁琐程度。

二、高考中的应用举例

例1.【2008全国Ⅱ】

（1）求f（x）的单调区间；

（2）如果对任何x≥0，都有f（x）≤ax，求a的取值范围。

（2）因为对任何x≥0，都有f（x）≤ax，于是a＞0

且函数y=ax是增函数，因此只需研究x∈［0，2π）情形。又当x∈［π，2π］时，f（x）≤0，即只需研究x∈［0，π）情形。①当x=0时，a∈R

其中k为函数图象上点（x，g（x））与点（0，g（0））连线的斜率。

在

故k为单调递减的函数。

例2.已知函数f（x）=（1+x）lnx；

（1）求f（x）=1处的切线方程。

解：（1）切线方程为y=2x-2

（2）当x∈（0，1）时，f（x）＜0，x-1＜0，g（x）＜-2故a＜0；

下面考查h（x）=（1+x）lnx的函数性质。

h′（x）＞h′（1）=2＞0

所以h（x）在（0，1）上是上凸的单调递增函数，故k为单调递减的函数。

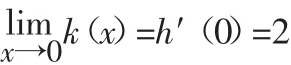
综上所述a的取值范围是a∈［-1，0）。

例3.【2011年高考全国新课标卷理科21】

（1）求a、b的值；

解：（1）a=b=1

其中m为函数图象上点（t，p（t））与点（1，p（1））连线的斜率。

p（t），p′（t），p′′（t）在区间（0，+∞）上的情况如下：

?

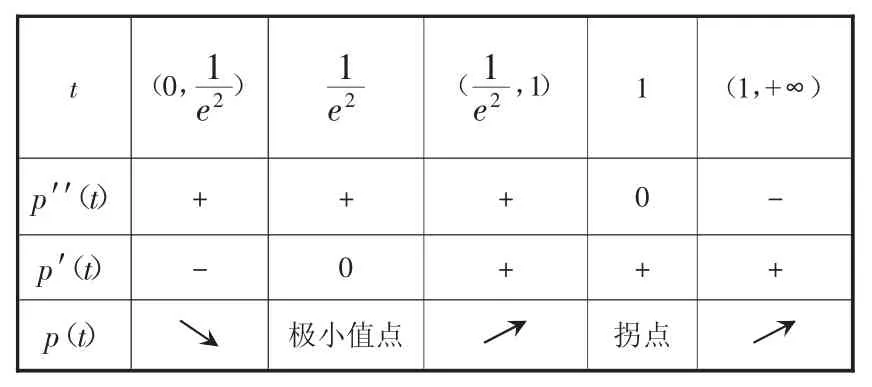
综上所述a的取值范围是k≤0。

三、教学反思

在高中数学中，有关函数和不等式的问题，学生大多数想到就是构造函数，通过求导证明单调性来研究问题。经过多年的训练，学生已经形成了思维定势，很难有新的突破。其实跳出固有思维，利用函数图象直观地理解问题，抓住问题的本质，往往可达到柳暗花明的效果。导数的本质是斜率的极限，从这个意义上来说，斜率更是至关重要。

熊欣，徐章韬.拉格朗日中值定理的初等化应用［J］.数学通讯，2012（07）.

·编辑 温雪莲