一种基于方向行波的多端VSC-HVDC系统保护策略

李 岩， 龚雁峰， 姜 斌

(华北电力大学， 北京 102206)

一种基于方向行波的多端VSC-HVDC系统保护策略

李 岩， 龚雁峰， 姜 斌

(华北电力大学， 北京 102206)

针对星型连接的多端柔性直流输电(VSC-HVDC)系统，提出一种基于方向行波小波能量比值的保护策略。首先分析了星型连接VSC-HVDC系统故障行波的传播特性，找出故障线路和非故障线路方向行波的不同传播规律；然后对电压和电流线模分量进行离散小波变换，计算相应线路方向行波的小波能量；最后通过各个线路正反向行波小波能量的比值确定故障线路。PSCAD/EMTDC仿真结果表明：提出的方法能够快速准确地判断星型拓扑VSC-HVDC系统的故障线路，并且不受故障线路、故障距离、故障类型和故障电阻的影响，具有很好的鲁棒性。

VSC-HVDC；星型拓扑；方向行波；离散小波变换；小波能量

基于电压源型的多端柔性直流输电技术(multi-terminal VSC-HVDC)在风电场并网、孤岛供电和城市电网供电等诸多领域具有非常广阔的应用前景[1-5]。多端直流输电系统通过采用环网或者星型的拓扑结构进行连接，由于换流站的控制方式和连接结构的灵活性，给系统保护策略的整定带来了极大的困难[6]。对于现有的多端直流输电工程，通常采用双极电缆的传输方式，故障类型多为永久性故障。当直流线路发生短路故障，短路电流将会传导至所有相连换流站，给系统的安全稳定运行带来巨大的挑战。因此，对于多端直流输电系统，当直流线路发生短路故障时应能够及时准确地确定故障线路并予以切除。

行波保护因其响应时间快，受故障电阻和故障位置影响小等优点，已经广泛作为直流线路的主保护，应用于多端直流系统中[7-12]。文献[13]针对环网结构的VSC-HVDC系统，根据边界行波的传播特点，提出一种边界保护的策略。文献[14]则针对星型连接的多端VSC-HVDC，基于同步测量装置捕捉各个端点行波到达时刻，实现对故障线路的判别和故障定位。文献[15]则通过行波和模糊算法实现对多端柔直系统故障线路的确定。本文针对星型连接的VSC-HVDC输电系统，提出一种基于方向行波小波能量比值的保护策略。

1 小波理论

1.1 小波变换

小波变换作为新型数字信号处理工具，最大的特点就是具有良好的时频局部化能力,能够同时从时域和频域描述奇异信号的每一个细节。故障产生的行波是一种非平稳变化的高频信号，因此小波变换成为分析行波最为有效的数学工具之一[16]。

(1)

连续小波变换(CWT)能有效避免信息丢失，但也导致了信息冗余，因此工程领域更常采用离散小波变换(DWT)进行分析计算。离散小波变换不仅能降低连续小波的冗余度，也能较好地保持连续小波变换的紧支性、光滑性和对称性，具有很好的工程应用效果。二进制离散小波变换的定义如下：

(2)

可以看出，离散小波变换只是对连续小波函数的尺度因子进行了二进制离散化处理，而保持时移因子的时间连续性，本文在处理行波信号时均采用离散小波变换。

1.2 小波能量

由小波理论可知，信号奇异点的时刻和大小可以通过小波变换局部极大值(即模极大值)的时刻和大小来描述。小波变换的模极大值点与信号突变点是一一对应的，模极大值与信号突变量的大小成正比。因此，可以通过小波变换模值的能量函数来描述信号的奇异性。信号在尺度J下的小波能量的定义如下[17]：

(3)

其中，dji表示在尺度J下离散小波变换的细节系数(即模值)，M表示采样周期内采样点的个数。

2 保护原理

2.1 故障行波基本理论

如图1所示，当输电线路某处发生短路故障，由叠加理论可知，相当于在故障点附加一个大小相等方向相反的电压源，产生的行波从故障点开始沿线路向两侧传播，并在波阻抗不连续处发生折反射。

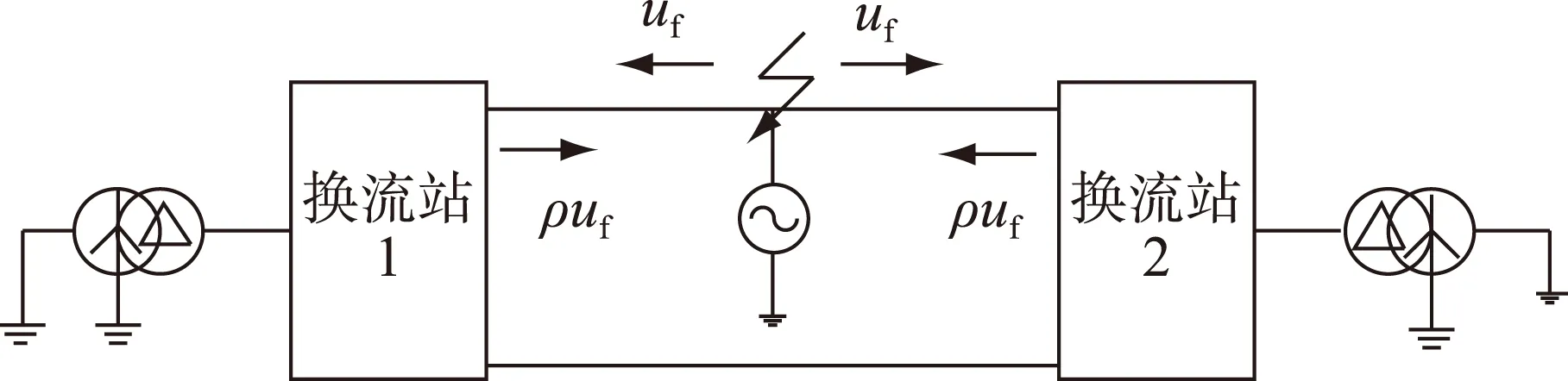
图1 直流线路故障分量

对于线路上距离故障点为x的任一点，可得该点的暂态电压Δu和暂态电流Δi分别为：

(4)

(5)

由式(4)和(5)可以得到正向行波和反向行波的表达式分别为：

(6)

(7)

2.2 正反向行波的特性分析

考虑如图2所示星型连接的VSC-HVDC输电系统，0代表星型节点，线路l01, l02和l03分别装有相应的保护装置。假设线路l03发生正极接地故障，其行波传播路径如图2所示。

图2 星型连接的VSC-HVDC输电系统

(8)

2.3 基于方向行波小波能量的保护策略

针对图2所示的星型连接的多端VSC-HVDC输电系统，将采样装置设置在星型节点处，这样可以同时检测3条线路的行波变化，并能够采用统一的启动判据标准，减小行波在线路上衰减所带来的影响。将相电压和电流解耦成模量进行分析，因为线模分量相对稳定，所以一般采用电压和电流的线模分量进行分析。基于方向行波小波能量的保护策略如下：

(1) 启动判据。对线模电流采用离散小波变换，设定合适的阈值，当小波变换的模值大于所设定的阈值时，启动方向行波小波能量的积分判据，对于噪声信号的干扰，可以采用多层小波变换来排除。

(2) 方向行波小波能量计算。将直流线路采样得到的电压和电流进行相模转换，得到相应线路的线模电压um1和电流im1，模量分解矩阵如下所示：

(9)

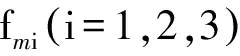
(3) 方向行波小波能量判据。根据方向行波小波能量的比值可以快速检测出故障线路，条件如表1所示。

表1 方向行波小波能量判据

3 算例分析

以PSCAD/EMTDC为仿真平台，搭建如图2所示的仿真模型。线路长度分别设置为l01=100 km，l02=100 km和l03=100 km。采样装置设置在星型节点处，采样频率设置为200 kHz。采用db 4母小波进行离散小波变换[16]。

3.1 典型故障分析

在线路l03设置正极接地故障，故障电阻设置为10 Ω，故障距离换流站3为30 km，故障开始时间为2 s，小波能量计算时窗为2 ms。

(1) 启动判据。以线模电流作为启动判据，线路l03线模电流的3层小波变换模值如图3所示。通过图3可以看出，小波变换的模值随着尺度的增加而变大，因此判断线路发生短路故障而非噪声信号。

图3 故障电流的三层小波变换模值

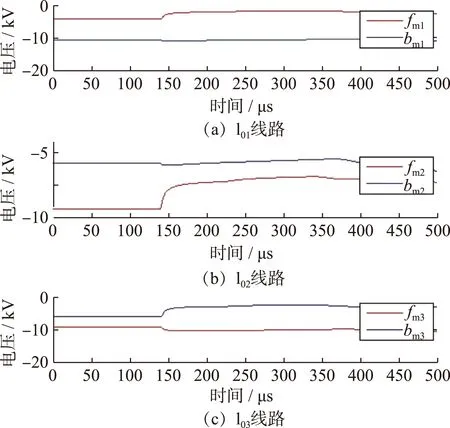
图4 线路正向和反向行波

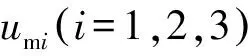
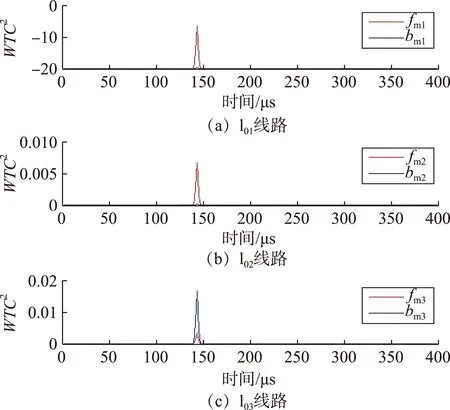
图5 正向和反向行波小波能量

(3)方向行波小波能量判据。根据小波能量结果计算方向行波的比值判据，可得Efm1/Ebm1=39.14，Efm2/Ebm2=38.70和Efm3/Ebm3=0.219。因此，可以判断故障在线路l03内，保护应快速动作予以切除。

3.2 适应度分析

采用与上述仿真相同的参数设置，分别针对不同故障线路，故障类型、故障距离和故障电阻进行仿真分析。

3.2.1 故障线路

分别在距离换流站1、换流站2和换流站3的30%处设置正极接地故障，故障电阻设为10 Ω，计算结果如表2所示。结果表明，该算法能够在不同线路故障时有效地识别出故障线路。

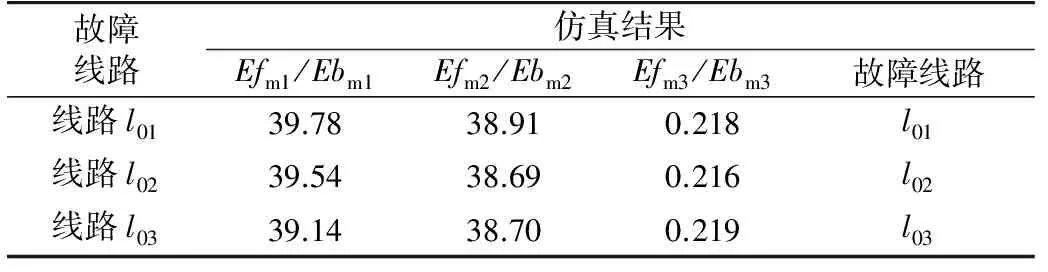
表2 不同故障线路

3.2.2 故障类型

在线路l03上设置短路故障，距离换流站30 km，接地电阻为10 Ω，分别设置正极接地，负极接地和极间短路故障，计算结果如表3所示。从表3中可以看出，该算法不受故障类型的影响。

表3 不同故障类型

3.2.3 故障距离

在线路l03上设置正极接地故障，距换流站3长度分别为线路的10%，30%，50%，70%，90%，计算结果如表4所示。从表4中可以看出，该算法不受故障距离的影响。

表4 不同故障距离

3.2.4 故障电阻

在线路l03上设置正极接地故障，距离换流站3长度为线路的30%，故障电阻依次设置为0.1 Ω、10 Ω、100 Ω和300 Ω，计算结果如表5所示。从表5中可以看出，即使在高阻的情况下，该算法仍能够有效地识别出故障线路。

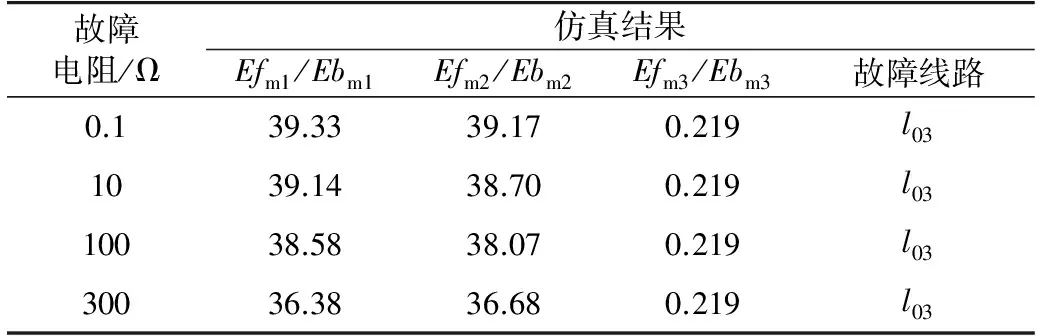
表5 不同故障电阻

4 结束语

针对星型连接的VSC-HVDC输电系统，提出了基于方向行波小波能量比值的保护策略。得到以下结论：(1) 通过方向行波的传播特性可以发现，对于故障线路，反向行波的幅值要大于正向行波，而非故障线路则相反；(2) 通过对方向行波采用离散小波变换和计算方向行波的小波能量比值的计算能够准确地确定故障线路；(3) 通过仿真得出，该算法不受故障线路、故障距离、故障类型和故障电阻的影响，具有很好的鲁棒性。

[1] 徐 政, 薛英林, 张哲任. 大容量架空线柔性直流输电关键技术及前景展望[J]. 中国电机工程学报, 2014，34(29): 5051-5062.

[2] 尹寿垚, 翟 毅, 吴 昊, 等. 基于柔性直流输电技术的分布式发电在城市电网中的应用[J]. 江苏电机工程, 2013, 32(4): 9-12.

[3] TANG L, OOI B T. Locating and Isolating DC Faults in Multi-Terminal DC Systems[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1877-1884.

[4] 张广明, 田 炜. 海上风电场VSC-HVDC并网不对称故障负序电流控制[J]. 江苏电机工程, 2014, 33(6): 7-11.

[5] 王志新, 吴 杰, 徐 烈, 等. 大型海上风电场并网VSC-HVDC变流器关键技术[J]. 中国电机工程学报, 2013，33(19): 14-26.

[6] GOMIS-BELLMUNT O, LIANG J, EKANAYAKE J, et al. Topologies of Multiterminal HVDC-VSC Transmission for Large Offshore Wind Farms[J]. Electric Power Systems Research, 2011, 81(2): 271-281.

[7] 李爱民, 蔡泽祥, 李晓华. 直流线路行波传播特性的解析[J]. 中国电机工程学报, 2010, 30(25): 94-100.

[8] 束洪春, 田鑫萃, 董 俊, 等. ±800 kV云广直流输电线路保护的仿真及分析[J]. 中国电机工程学报, 2011, 31(31): 179-188.

[9] SONG G B, CAI X L, GAO S P, et al. Natural Frequency Based Protection and Fault Location for VSC-HVDC Transmission Lines[C]∥ International Conference on Advanced Power System Automation and Protection. IEEE, 2011: 177-182.

[10] 艾 琳. 高压直流输电线路行波保护的研究[D]. 北京： 华北电力大学, 2002.

[11] 武 骁, 何正友, 彭少博, 等. 基于行波固有频率的特高压直流输电线路纵联保护方法[J]. 电力系统保护与控制, 2013(11): 67-73.

[12] 高 杉, 林 圣, 何正友. 基于并联电容参数识别的VSC-HVDC输电线路纵联保护[J]. 电网技术, 2015, 39(7): 2002-2009.

[13] XU Y, SHI D F, YAN S B. Boundary Protection Strategy for the VSC-MTDC under DC Faults[J]. Applied Mechanics & Materials, 2013, 448-453: 2030-2035.

[14] NANAYAKKARA O M K K, RAJAPAKSE A D, WACHAL R. Traveling-wave-based Line Fault Location in Star-Connected Multiterminal HVDC Systems[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2286-2294.

[15] HOSSAM-ELDIN A, LOTFY A, ELGAMAL M. Combined Traveling Wave and Fuzzy Logic Based Fault Location in Multi-terminal HVDC Systems[C]∥ 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, 2016: 1-6.

[16] LI W, MONTI A, PONCI F. Fault Detection and Classification in Medium Voltage DC Shipboard Power Systems With Wave-lets and Artificial Neural Networks[J]. IEEE Transactions on Instrumentation & Measurement, 2014, 63(11): 2651-2665.

李 岩

李 岩(1990 —)，男，辽宁海城人，博士，研究方向为柔性直流输电的保护与控制；

龚雁峰(1977 —)，男，江苏启东人，教授，博士生导师，研究方向为电力系统保护与控制；

姜 斌(1990 —)，男，江苏扬州人，博士，研究方向为柔性直流输电的保护与控制。

A Protection Scheme for Multiterminal VSC-HVDC System Based on Direction Traveling Waves

LI Yan，GONG Yanfeng，JIANG Bin

(North China Electric Power University, Beijing 102206, China)

A protection scheme based on the ratio of energies of direction traveling waves is presented in this paper. Firstly, the propagation characteristic of fault traveling waves in a star-connected VSC-HVDC system is analyzed, and the different propagation law between fault and non-fault lines is studied. Then modal voltage and current are transformed in discrete wavelet transform(DWT), and wavelet energies of direction traveling waves are calculated. Finally, the fault line is determined by the ratio of positive and negative direction traveling waves. Simulation results of PSCAD/EMTDC show that the proposed method can identify the fault line quickly in the star-connected VSC-HVDC system. The proposed method is insensitive to different fault lines, fault distance, fault types and fault resistance, and has good robustness.

VSC-HVDC；star-connected；direction traveling waves； discrete wavelet transform； wavelet energy

2016-10-24；

2016-11-25

国家电网公司科技项目(SGZJ0000BGJS1500265)

TM315

A

2096-3203(2017)01-0070-04