一维广义Cantor集上拟对称映射的等价刻画

李彦哲

(1.广西大学数学与信息科学学院，广西 南宁 530004；2.华南理工大学数学学院，广东 广州 510641)

一维广义Cantor集上拟对称映射的等价刻画

李彦哲1,2

(1.广西大学数学与信息科学学院，广西 南宁 530004；2.华南理工大学数学学院，广东 广州 510641)

对满足几何正则条件的一维广义Cantor集之间的拟对称映射，给出等价刻画.

拟对称映射；广义Cantor集；几何正则

0 引言

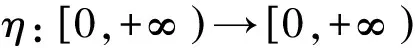
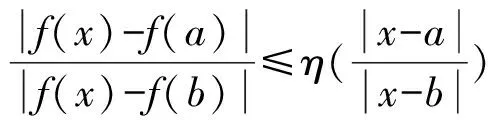
拟对称映射来源于1956年Beurling等[2]对上半平面到其自身的拟共形自同胚的边界问题的研究.拟对称映射在一般度量空间中的定义于1980年由Tukia等[3]给出.Vaisala等[4-5]还证明了高维欧氏空间中拟对称映射与拟共形自同胚是等价的.作为一种同胚，拟对称映射除了保持集合的拓扑性质外，还保持集合的许多度量性质和几何性质[1]，在度量空间分析学中起着重要的作用.

本研究的是分形集上的拟对称映射，对拟对称映射对分形集分形维数的改变的研究是近年来国内外学者研究的一个热门课题，相关文章有很多(如文献[6]).分形集上的拟对称映射有许多良好的性质，所以判断一个分形集上的映射是否为拟对称映射是很有必要的，但拟对称映射的定义比较复杂，对于一个同胚，判断其是否为拟对称映射是比较困难的，我们需要对拟对称映射进行一些等价刻画，用一些相对简单的等价条件来刻画拟对称映射.为解决这个问题，1980年Tukia等[3]提出了弱拟对称映射的概念：如果对于同胚f:X→Y，存在常数H>0，使得对任意3个不同点a,b,x∈X有，

则称f为一个弱(H-)拟对称映射.

易验证拟对称映射必是弱拟对称映射，但反之不然.那么自然就会产生一个问题：拟对称映射与弱拟对称映射在什么情况下等价？

关于这个问题Vaisala[7]和Heinonen[1]给出了连通集上的拟对称映射与弱拟对称映射等价的一个条件：连通加倍空间到加倍空间上的拟对称映射与弱拟对称映射等价. 但我们遇到的分形集通常是全不连通的，从而我们自然地会有一个问题：连通性可否减弱？但在文献[8]中可知，即使对于满足开集条件或强分离条件的自相似集，也不一定成立文献[7]和[1]中的结论.为此， Li[8]在2015年导出弱(λ,H)-拟对称映射的概念，证明了实直线上满足λ-small gap条件的一维Moran集到加倍空间的拟对称映射与弱 (λ,H)-拟对称映射等价；并且对几何正则的一维Moran集之间的拟对称映射给出了一个等价刻画.进一步，我们在2016年将文献[7]中的第一个结果推广到一致完全空间以及一维广义Cantor集上[8]，得到紧λ-一致完全空间到加倍空间的拟对称映射以及满足λ-small gap条件的一维广义Cantor集到加倍空间的拟对称映射与弱(λ,H)-拟对称映射是等价的.一维广义Cantor集比一维Moran集范围更广泛，那么对一维广义Cantor集之间的拟对称映射，我们能否像文献[8]对几何正则的一维Moran集的一样，给出等价刻画呢？本文中对此进行了研究，证明了对于几何正则的一维广义Cantor集，也可以进行类似的等价刻画.

下面，给出本文中的主要结论：

定理 设E和E′都是几何正则的一维广义Cantor集，f是E到E′的双射，那么f是拟对称映射当且仅当下面3个条件成立：

1)对于所有柱集Eσ，f(Eσ)是既开又闭的集合；

3)L(f(Eσ*i))-L(f(Eσ))≤c对所有σ和i成立，

其中c>0为常数.

本文由下面两部分构成：第一部分介绍一些预备知识，包括弱(λ,H)-拟对称映射，一维广义Cantor集，几何正则等定义，以及需要用到的已知引理；第二部分是定理的证明.

1 预备知识

定理的证明需要用到弱(λ,H)-拟对称映射，给出其定义：

定义1.1[7](弱(λ,H)-拟对称映射) 设X和Y为两个度量空间，f为X到Y的同胚，若存在常数λ>0及H>0，使得任意3个不同点a,b,x∈X都满足

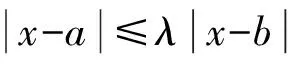
则称f为一个弱(λ,H)-拟对称映射.

注：当λ=1时，弱(λ,H)-拟对称映射与弱(H-)拟对称映射等价；(η-)拟对称映射都是弱(λ,η(λ))-拟对称映射; 当λ>1时，弱(λ,H)-拟对称映射都是弱(H-)拟对称映射；当0<λ<1时，弱(H-)拟对称映射都是弱(λ,H)-拟对称映射.

定义1.2[9](一维广义Cantor集) 设J⊂是闭区间，J的闭区间族F={Jσ：σ∈Ω}称为具有广义Cantor结构，若它满足：

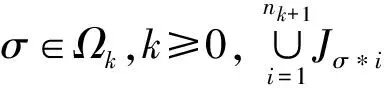
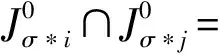
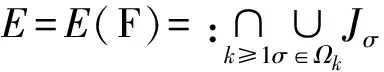
记⊂{J，nk}为所有满足i)ii)iii)的一维广义Cantor集族.

本文中，我们假设对∀σ∈Ωk，k≥0，Jσ*1，Jσ*2，…，Jσ*nk+1从左至右排列.如果Jσ*1，Jσ*2，…，Jσ*nk+1不是从左至右排列，我们也可以类似证明本文中的结论.

注：直线上满足开集条件的自相似集是一类特殊的一维广义Cantor集，一维Moran集也是一类特殊的一维广义Cantor集，与一维Moran集相比，一维广义Cantor集去掉了上下两级基本区间长度比的限制，一维广义Cantor集E的k阶基本区间Jσ与包含在Jσ中的任意k+1阶基本区间Jσ*i(1≤i≤nk+1)的长度比与阶数k无关.

下面引入一个重要定义：small gap条件.

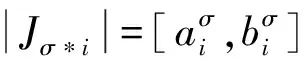
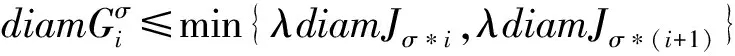
则称E满足(λ-)small gap条件，其中diam表示集合的直径.

引理1.1[6]设E为满足(λ-)small gap条件一维广义Cantor集，λ≥1，Y为加倍空间，则映射f:E→Y是拟对称映射当且仅当存在H>0，使得f是弱(λ,H)-拟对称映射.

定义1.4(几何正则) 如果E∈⊂ {J，nk}满足c*>0且δ*>0，则称一维广义Cantor集E为几何正则的.

如果存在两度量空间X与Y之间的拟对称双射，则称X与Y拟对称等价.David和Semmes[9]得到了: 两加倍、一致完全且一致不连通的紧度量空间是拟对称等价的.几何正则的一维广义Cantor集是紧集，并且是加倍、一致完全且一致不连通的，所以任意两个几何正则的一维广义Cantor集之间一定存在拟对称双射，本文中的定理给出了这些拟对称双射的等价刻画.

为了后面的证明方便，我们给出以下几个记号：设E∈⊂ {J，nk}是几何正则的一维广义Cantor集，对任意σ∈Ω，记Eσ=E∩Jσ，我们称Eσ为E的柱集.由δ*>0得柱集是即开又闭的集合.设A⊂E，定义：

2 定理的证明

必要性的证明：因为Eσ是柱集，所以Eσ既开又闭，又因为f为拟对称映射，则f是一个拓扑同胚，所以f(Eσ)既开又闭，i)成立.

为证明ii)，取x,a∈Eσ以及b∈EEσ使得

(1)

从而有

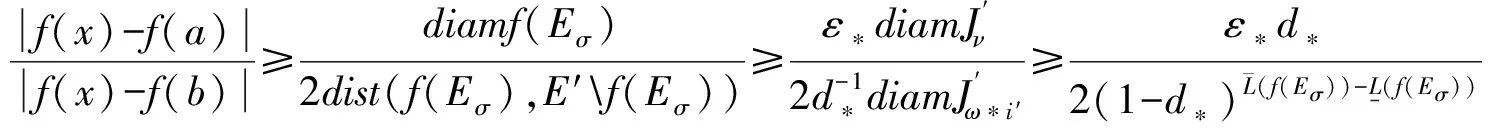
另一方面，取τ使得x,b∈Eτ和x∈Eτ*i″,b∈Eτ*j″(i″≠j″)，注意到Eσ⊂Eτ，我们有

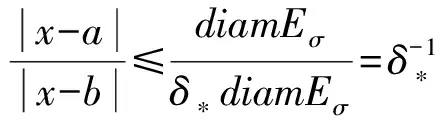
得到

(2)

为证明iii)，取x,b∈Eσ*i以及a∈Eσ，使得

从而

(3)

(4)

由(3)-(4)式，利用f为(η-)拟对称映射，得到

从而

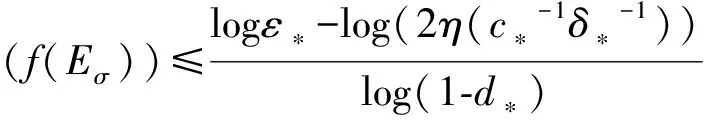
(5)

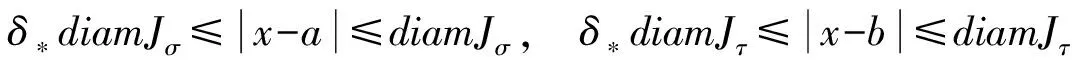
(6)

由L的定义，我们有

(7)

(8)

注意(8)式中我们用到了条件 ii)和iii).

若E不是端点正则，我们考虑结构与E相近的端点正则一维广义Cantor集F，先构造满足本文中定理条件的双射g:F→E′，再验证g是拟对称映射，最后通过g与f的关系来证明f是拟对称映射.分析如下：

若E∈⊂ {J，nk}，其压缩比和间隔比下界分别为c*和δ*，考虑F∈⊂ {I，nk}，其中I∅=I=J，且对任意σ∈Ωk-1(k≥1)满足：

1)Iσ*1,Iσ*2,…,Iσ*nk为从左至右排列的Iσ的闭子区间；

2)Iσ*1与Iσ左端点重合且Iσ*nk与Iσ右端点重合；

3)dist(Iσ*i,Iσ*(i+1))=dist(Iσ*(i+1),Iσ*(i+2))对任意1≤i≤nk-2成立；

设g=f。π：F→E′,则由π的定义及f满足本文中定理的条件i)ii)iii)，得到g满足本文中定理的条件i)ii)iii)，又因为一维广义Cantor集F端点正则，所以g是拟对称映射.又因为f=g。π-1为两拟对称映射的复合映射，所以f是拟对称映射.这样就完成了定理充分性的证明.

致谢 感谢华南理工大学吴敏教授和熊瑛副教授在论文撰写中给予的指导和帮助.

[1] Heinonen J. Lectures on analysis on metric spaces[M]. New York:Universitext Springer-Verlag, 2001.

[2] Beurling A, Ahlfors L. The boundary correspondence under quasiconformal mappings[J]. Acta Math, 1956,96: 125-142.

[3] Tukia P,Vaisala J.Quasisymmetric embeddings of metric spaces[J].Ann Acad Sci Fenn Ser A I Math,1980,5(1):97-114.

[4] Heinonen J, Koskela P.Definitions of quasiconformal mappings[J]. Ann Acad Sci Fenn Ser A I Math, 1995,120(1):61-79.

[5] Vaisala J. Lectures on n-dimensional quasiconformal mappings[M]. Berlin-New York:Lectures notes in Mathmatics (volume 229 of Springer-Verlag), 1971.

[6] Li Y Z, Yang J J. On the equivalence of weak quasisymmetry and quasisymmetry on non-connected sets[J], J Math Anal Appl, 2016,435(2):1400-1409.

[7] Vaisala J. The free quasiworld. Freely quasiconformal and related maps in Banach spaces[J]. Polish Acad Sci, 1999,48:55-118.

[8] Li Y Z. Quasisymmetric mappings on Moran sets[J].Acta Mathematica Sinica:English Series, 2015,9(31): 1424-1434.

[9] David G, Semmes S. Fractured fractals and broken dreams,volume 7 of Oxford Lecture Series in Mathematics and its Applications[M]. New York:The Clarendon Press Oxford University Press, 1997.

(责任编辑 赵燕)

The equivalence of quasisymmetric mappings on 1-dimensional Cantor-like sets

LI Yanzhe

(College of Mathematics and Information Science， Guangxi University， Nanning 530004， China;College of Mathematics，South China University of Technology， Guangzhou 510641， China)

We gave a equivalent condition to the quasisymmetic mappings between two 1-dimensional geometrically regular Cantor-like sets.

quasisymmetic mapping; Cantor-like sets; geometrically regular

2016-05-15

国家自然科学基金天元基金(11626069)、广西大学科研基金(XJZ150827)资助

李彦哲(1986-)，男，博士，讲师，E-mail: lyzkbm@163.com

1000-2375(2017)01-0087-06

O174.12

A

10.3969/j.issn.1000-2375.2017.01.017