剖析与二次函数图象有关的最值问题

林荣坤

摘要：对于二次函数的最值问题，我们在初中就开始接触，而且也是初中的重要教学内容，但也只是注重基础，涉及的也是简单的二次函数。随着知识的加深，二次函数的最值问题涉及的内容越发的广泛与深奥。作为二次函数中最基本的问题——最值问题，本文将从简易到复杂的知识进行剖析。

关键词：二次函数；最值

对于二次函数图象的最值问题，重点关注的主要是图象的对称轴和所给自变量的区间（即定义域）的界定。而且掌握二次函数的最值问题，首先需要将二次函数的图象形象的画出来。然后根据图象以及问题的条件界定来进行最值问题的求解。

一、二次函数的图象

对于二次函数的图象，我们需要找到二次函数的对称轴，顶点以及开口方向，有时还需要界定某一到两个特殊的线与x-y轴的交点，才能较为准确的描绘出图象。

二次函数的的表达式有顶点式，交点式以及三点式，其一般的表达式为y=ax?+bx+c（a≠0），此图象的对称轴，开口方向以及顶点都取决于这一般表达式中的a、b、c三个系数。最重要的是求解对称轴，对称轴的计算公式为x=-b/2a。

其一般图形为：

二、二次函数图象的最值

1、二次函数在界定区间上的最值问题（最简单，直接的最值问题）

此类问题基本就是明确给定二次函数以及定义域区间的情况下，求最值的。解决方案就是找到此函数的对称轴，看其与定义区间的关系，在判断在此区间上函数的增减性，进而求出答案。

例如：已知二次函数y=x2-2x，求在区间[0，4]上的最值。

根据二次函数可以画出图象，对称轴为x=1，草图如下：

从图中可以看出在区间[0，4]上，y值先递减后递增，在对称轴x=1处取得最小值y=-1，在x=4处取得最大值y=8.

2、二次函数在不定区间上的最值问题（相对上一个，有些复杂，需要分类）

此类问题是在明确给定二次函数，但是其自变量的定义区间是变动的（存在未知数）情况下求解最值的。然而此类问题的解决方法就是通过明确给定的二次函数画出图象，再根据对称轴与自变量的关系界定进行分类讨论，最后分别判断在此区间上的增减性，求得最值。

例如：已知二次函数y=x2/2-x-5/2，求在[t，t+1]上的最小值。

根据二次函数y=x2/2-x-5/2可以得出对称轴x=1，图象开口向上，再分类，画草图。

第一类：当对称轴x=1在所给区间的左侧，即t≧1，草图如下：

从图中可以看出，在区间[t，t+1]上，函数递增，最小值为x=t时，y=t2/2-t-5/2。

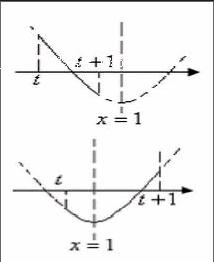
第二类：当对称轴x=1在所给区间的右侧，即t+1≦1→t≦0，草图如下：

从图中可以看出，在区间[t，t+1]上，函数递减，最小值为x=t+1时，y=t2/2-3。

第三类：当对称轴x=1在所给区间的内，即t<1

从图中可以看出，在区间[t，t+1]上函数先减后增，最小值为x=1时，y=-3。

若是还需求最大值，前两种可以直观的看出，而最后一种需要对比在x=t以及x=t+1时y值得大小。此时t的范围还需划分。

当x1=t时，y1=t2/2-t-5/2，当x2=t+1时，y2=t2/2-3

y1-y2=1/2-t，从式子中可以看出当0

3、不确定的二次函数在固定区间下的最值问题

此问题是在明确给出定义域而二次函数存在未知系数（图象不确定）的情况下，求最值的问题。此类问题可以先将二次函数有一般形式转换为顶点式，找出其对称轴，开口方向以及区间位置。最重要的是找到其对称轴，然后根据未知系数分类进行求解，最后判断增减性，求最值。

例如：已知二次函数y=bx2+4bx+b2-1，求在区间[-4，1]上的最大值。

根据二次函数y=bx2+4bx+b2-1，写成顶点式y=b（x+2）2+b2-4b-1，可以看出对称轴为x=-2，在区间[-4，1]上，只需根据图象开口方向来判断区间的最大值。

第一类：当b=0时，y=-1，无最大最小值之说

第二类：当b<0时，图象开口向下，草图如下：

从图中可以看出，在区间[-4，1]上函数先增后减，最大值为当x=-2时，y=b2-4b-1。

第三类：当b>0时，图象开口向上，草图如下：

从图中可以看出，在区间[-4，1]上函数先减后增，最大值为区间的临界点，需要判定。

当x1=-4时，y1=b2-1

当x2=1时，y2=b2+5b-1

因为b>0，可以看出y1=b2-1

4、二次函数已知区间和最值求未知函数的系数（此类最为复杂，分类情况较多）

此类函数是在明确给出自变量区间，以及在区间内最值得一个（最大或最小），求解未知函数的系数。此类问题通常不会给定对称轴，因此需要进行分情况进行判定来求解，再根据其给出的最值来求出位置系数，此类问题通常的解有时会与条件分类的情况不相符，因此不要因为求出一个就大意，要注意情况与解的一致性。

例如：已知二次函数y=x2-2ax-1，已知函数在区间[0，2]上的最小值为-2，求a的值。

根据二次函数y=x2-2ax-1，写成顶点式y=（x-a）2-a2-1，对称轴为x=a，图象开口向上，然后进行分类

第一类：当a≦0时，画出草图如下：

从图中可以看出，函数在区间[0，2]上是递增的，最小值为当x=0时，y=-1，与题中最小值为-2不相符。此分类舍弃。

第二类：当a≧2时，画出草图如下：

从图中可以看出，函数在区间[0，2]上是递减的，最小值为当x=2时，y=3-4a，因为题中给出最小值为-2，所以3-4a=-2求得a=5/4<2与条件不符的，舍弃。

第三类：当0

从图中可以看出，函数在区间[0，2]上是先减后增的，最小值为当x=a时，y=-a2-1因为题中给出最小值为-2，所以-a2-1=-2求得a=1或者-1，再根据分类条件0

综上得出a=1。

还存在第二种情况，图象的开口方向与未知参数有关，则划分情况求解释更需注意。

例如：二次函数y=ax2-2ax-1，已知函数在区间[0，2]上的最小值为-2，求a的值。

先根据二次函数y=ax2-2ax-1，将其换算成顶点式为y=a（x-1）2-a-1，可以得知对称轴为x=1，但开口方向不确定，需要分类进行求解。

第一类：当a=0时，y=-1与已知条件不相符，舍弃。

第二类：当a>0时，可以画出草图：

从图中可以看出，在区间[0，2]函数先减后增，最小值为对称轴即x=1时的y=-a-1，由已知条件最小值为-2，得出a的值为1，符合条件a>0。

第三类：当a<0时，可以画出草图：

从图中可以看出，在区间[0，2]上函数先增后减，最小值为区间端点值，需要进行比较。当x=0时，y=-1；当x=2时，y=-1，而此种情况下，最小值只能是-1，与已知条件相违背，舍弃。

所以综上得出a=1。

对于这两道题相对来说简单，要么给定了开口方向，要么给定了对称轴而且区间端点关于对称轴对称。但是有时题中既不会给定对称轴也不给定开口方向，就需要结合这两道题综合考虑未知系数的值，题目就会相对复杂。你只需要找准全部的区间，并且针对分类情况，将所有的值求出即可。

通过剖析二次函数图象的最值问题，可以看出关键点在于图象的对称轴以及区间的界定，以及在分情况求解中条件的限定。其实对于二次函数图象的最值问题，能画出大概的草图会有利于对于最值的把握，但是也不能一概而论，毕竟是草图，不能主观判断。记住这几点，然后在求解二次函数的图象的最值问题时就会显得游刃有余。

参考文献：

[1]黄庭柏.浅谈如何引导学生学好二次函数[A].国家教师科研专项基金科研成果（华声卷2）[C].2015

[2]冯法.浅谈二次函数在高中数学中的重要作用[A].2015年9月现代教育教学探索学术交流会论文集[C].2015

[3]吴选根.26.3实际问题与二次函数（4）[A].2012年河北省教师教育学会教学设计主题论坛论文集[C].2012

[4] 史建军.一道最值问题的推广、完善与另解[J]. 中学数学研究. 2016

[5] 施伦.轨迹法求一类线段的最值[J]. 中小学数学（初中版）. 2016

[6] 蒋飞. 二次函数常见错误剖析[J]. 数学大世界（初中版）2014年