混凝土管片及其接头承载力特性数值模拟分析
李守巨,李雨陶,上官子昌,于 申
(1. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024;2. 大连海洋大学 海洋与土木工程学院,辽宁 大连 116023)
混凝土管片及其接头承载力特性数值模拟分析
李守巨1,李雨陶1,上官子昌2,于 申1
(1. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024;2. 大连海洋大学 海洋与土木工程学院,辽宁 大连 116023)
为了分析混凝土管片及其接头的力学特性,采用有限元方法数值模拟完整混凝土管片及其接头的承载力特性。混凝土本构关系采用Rush建议的二次抛物线和水平直线组合模型。钢筋采用弹性-理想塑性本构模型。采用杆单元模拟混凝土管片内的纵筋和箍筋以及管片接头处螺栓。研究不同轴力与弯矩组合作用下混凝土管片极限承载力的变化规律,分析正负弯矩作用下混凝土管片接头的承载力特性。研究表明,混凝土管片的极限弯矩随轴力的增大而增加;在最大轴力时与无轴力管片承载力相对比,管片极限弯矩增加70%。通过对管片接头研究发现,管片接头的极限承载力只是管片的40%左右;接头的存在降低了混凝土管片的承载能力,管片接头的极限弯矩大小主要受接头螺栓强度和位置的影响。
混凝土管片;管片接头;承载能力;数值模拟;极限弯矩;破坏过程
盾构法作为一种高效的施工技术,目前已逐渐被工程界普遍使用。混凝土衬砌管片作为盾构法的一种主要衬砌方式,其力学性能越来越被人们所关注。盾构隧道的混凝土衬砌是一种环状拼装结构,常由预制的6到9个管片拼接而成,管片和管片之间通过螺栓和止水衬垫连接,在对盾构隧道衬砌管片进行结构计算和模拟分析时,也必须考虑到多块管片之间的连接作用。管片的接头在很大程度上影响着整体衬砌的变形和承载能力,因此,管片接头的强度计算成为了整体衬砌设计过程中的重要问题。
确定管片承载力的方法主要有两种:一种是足尺试验,但由于足尺试验的试验成本较高,不易实行;另一种是将接头部分近似于混凝土截面进行计算,即将螺栓视为受拉钢筋,将接缝处截面视为混凝土截面来计算,但这种计算方法由于未考虑手孔作用、接缝的不连续性等性质,存在一定误差。因此,采用有限元方法分析盾构管片的力学特性越来越受到人们的重视,目前在管片接头力学特性方面已有不少的成果。Huang等[1]研究了由于纵向不均匀沉降引起的管片接头变形问题。Li等[2]实验研究了管片接头的纵向张开问题。张厚美等[3]通过有限元模拟值和实验值的对比,得到管片应力应变之间的变化规律。葛世平等[4]考虑对管片接头及其附近区域进行刚度修正,而管片其余区域保持原刚度不变,提出管片接头简化数值模拟方法——局部刚度修正法。俞涛等[5]通过三维有限元模拟,探讨了各结构参数对接头抗弯刚度的影响规律。Arnau等[6]采用三维计算模型研究了盾构隧道管片接头的力学特性问题。Blom等[7]利用实体单元对管片衬砌进行了三维分析。Chen等[8]采用有限元方法研究了盾构隧道管片破坏过程,并提出增加手孔和螺栓孔周围的混凝土强度能有效增加混凝土管片的使用寿命。Molins等[9]基于现场观测数据研究了混凝土管片的力学响应特性。Gong等[10]考虑隧道管片纵向非均匀沉降而引起的管片接头受力变化的问题。Yang等[11]研究了大尺度管片接头的三维模型问题[12]。周海鹰通过1∶1试验分析了试验加载方式和配筋率对钢筋混凝土衬砌管片破坏的影响。本研究采用有限元方法分别对混凝土管片及其接头进行数值模拟,得到整体管片和管片接头的极限承载力特性,对管片接头破坏机制进行分析,并为管片及其接头设计提出参考依据。
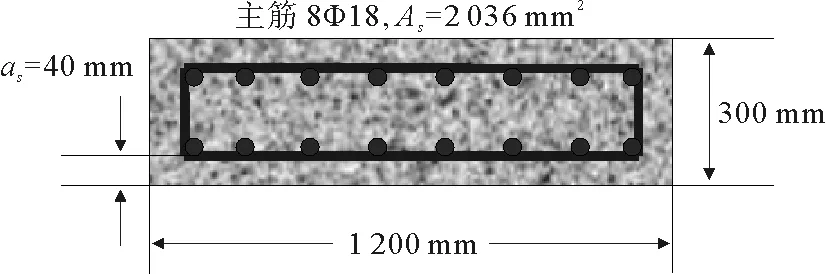
图1 管片配筋图Fig.1 Reinforcement of segment
1 混凝土管片承载力特性有限元模拟分析
1.1 模型建立及本构关系
利用有限元软件ANSYS模拟混凝土管片承载力特性。以北京地铁四号线某施工段为例[13],截面配筋如图1所示,管片宽度1 200 mm,厚度300 mm,取管片长度为2 960 mm。混凝土管片采用C50混凝土,抗压强度设计值为23.1 MPa;管片采用对称布筋,单块管片主筋采用8根直径为18 mm的HRB335钢筋,As=2 036 mm2;单块管片箍筋为8根直径为10 mm的HPB300钢筋,箍筋间距s=350 mm,Av=785 mm2。纵筋中心距管片外边界距离取as=40 mm。由于混凝土具有开裂、压碎和塑性变形的能力,因此采用ANSYS中用来模拟混凝土、岩石等抗压能力远大于抗拉能力的非均匀材料的Solid65单元来进行模拟。钢筋属于一种细长材料,通常忽略其横向剪切强度,只考虑轴向的拉压强度,因此选取杆单元Link180对其进行模拟。材料参数及单元类型选取见表1。为防止支座处和加载处因应力集中造成局部破坏,在支座与加载位置添加40 mm弹性垫块。
表1 模型材料参数表
Tab.1 Material parameters in model

构件名称单元类型截面尺寸/mm2弹性模量E/GPa泊松比v混凝土 Solid651200×30034.50.20主筋 Link180254.5210.00.30箍筋 Link18050.3200.00.25
混凝土本构方程采用Rush建议的二次抛物线和水平直线组合模型,本构关系方程如下:
。
(1)
式中:fc为混凝土的抗压强度设计值,σc为混凝土应变为εc时的混凝土压应力,ε0为对应混凝土应力刚达到fc时的应变,εcu为混凝土的极限压应变。其中n=2,ε0=0.002,εcu=0.003 3[14]。
混凝土张开裂缝的剪力传递系数取0.5,闭合裂缝的剪力传递系数取0.95[15]。钢筋的本构关系选取弹性-理想塑性模型,本构关系如下:
σs=Esεs,εs≤εy;
σs=Esεs=fy,εy<εs≤εu。
(2)
式中:σs为钢筋应力,εs为钢筋应变,Es为钢筋的弹性模量,fy为钢筋的屈服强度设计值,εy为钢筋达到屈服时的应变,εu为钢筋的极限应变。在极限状态情况下,混凝土的极限压应变取0.003 3,钢筋极限应变取0.01。

图2 模型加载图
模型加载模式如图2所示,模型加载参照单跨简支梁的受力模式,约束梁一端的所有位移,另一端约束竖向位移。本算例采用位移加载,即在距管片两端1 090 mm处,施加一个竖向位移,并通过分步加载,逐步得到混凝土管片的极限承载力。混凝土管片在土层内主要受到轴力和弯矩的共同作用,为得到不同轴力时混凝土管片的极限承载力,需在管片模型的两端施加水平荷载形成轴力,根据有限元模拟,管片在土层中所受轴力从500到1 000 kN变化,分别取轴力为500、600、700、800、900、1 000 kN进行加载。按上述条件建立混凝土管片有限元模型如图3,管片配筋模型如图4所示。

图3 混凝土管片有限元模型Fig.3 FEM model of concrete segment

图4 混凝土管片钢筋有限元模型
1.2 混凝土管片承载力有限元模拟计算结果分析
首先通过有限元模拟计算得到混凝土管片在无轴力作用下加载面的挠度-弯矩曲线如图5所示,极限状态下中截面压应力分布如图6所示。
由无轴力时的混凝土管片挠度-弯矩曲线可以看出混凝土管片受力的三个阶段。第一阶段为无裂缝工作阶段,此时混凝土与钢筋均为弹性变形,当弯矩达到Mcr=42 kN·m时混凝土发生开裂。第二阶段为带裂缝工作阶段,此阶段大部分受拉区混凝土退出工作,拉力主要由受拉钢筋承担,直到弯矩My达到151 kN·m时下部受拉钢筋屈服。在第三阶段混凝土管片受拉区裂缝急剧展开,受拉钢筋应力保持在屈服强度不变。随着弯矩增加直到受拉钢筋或受压区混凝土达到极限应变,混凝土管片达到极限弯矩Mu=197 kN·m,失去承载能力。

图5 无轴力时混凝土管片挠度-弯矩曲线图Fig.5 Deflection-bending moment curve of concrete segment without axial force

图6 混凝土管片极限状态中截面压应力分布

表2 不同轴力时混凝土管片极限弯矩
利用有限元模拟不同轴力下混凝土管片的挠度-弯矩曲线如图7所示。不同轴力时管片纵筋屈服时的弯矩和极限弯矩如表2所示,由ANSYS模拟结果发现在轴力小于500 kN时,管片的极限承弯矩主要由下部受拉钢筋决定,即当下部受拉钢筋达到极限应变时,上部受压区混凝土并未达到极限应变。而当轴力大于500 kN时管片的极限弯矩主要由受压区混凝土和受拉钢筋共同决定,即当受拉区钢筋达到屈服时,受压区混凝土也达到极限应变,此时管片视为破坏。挠度-弯矩曲线基本反映了钢筋混凝土管片的受力破坏特点,当跨中下部受拉钢筋达到屈服时,随着裂缝的不断展开,受压区混凝土面积逐渐减小,直到上部受压区混凝土压碎破坏,此时钢筋混凝土管片达到其极限承载力。通过对不同轴力下钢筋混凝土管片挠度-弯矩曲线分析可以看出,随着轴力的增加,管片在实际工况内,即轴力在500至1 000 kN之间,管片屈服弯矩和极限弯矩呈增加趋势(图8),与无轴力时相比较,管片极限弯矩的最大值增加70%。而且混凝土管片加载面的最大挠度也随轴力的增加而增加。

图7 不同轴力时混凝土管片挠度-弯矩曲线Fig.7 Deflection-bending moment curves of concrete segment with different axial forces
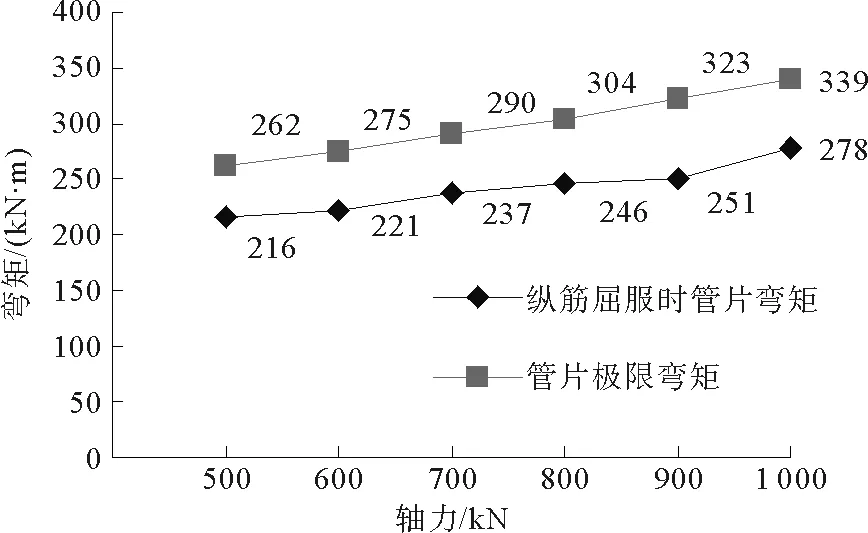
图8 管片极限弯矩随轴力的变化
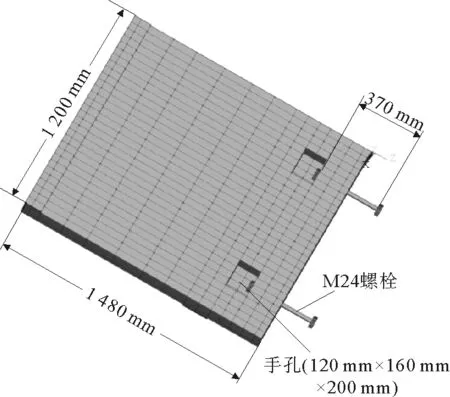
图9 带有螺栓的管片接头有限元模型(一半)
2 管片接头承载力特性的有限元模拟分析
2.1 管片接头模型建立
盾构隧道衬砌为拼装式衬砌,每个衬砌管片之间由接头螺栓连接,故接头处的力学特性对整体衬砌结构有很大影响。建立管片接头的有限元模型,管片接头混凝土截面尺寸与完整混凝土管片相同。螺栓中心距管片底面120 mm,手孔长宽高(130 mm×160 mm×200 mm),手孔距管片侧面160 mm。螺孔直径取28 mm,螺栓等级为A级M24,性能等级分别取6.8(屈服强度设计值为480 MPa)和8.8(屈服强度设计值为640 MPa)两种情况进行计算,螺栓有效直径21.19 mm,有效截面积352.5 mm2,螺杆长370 mm。螺栓本构采取弹性-理想塑性模型,采用Link180杆单元对螺杆进行模拟,并将其固接到由Solid95单元模拟的螺帽上。管片与管片之间,螺栓与管片之间的接触效应利用Contact174与Target170接触单元来模拟。混凝土与混凝土之间摩擦系数取0.5,混凝土与钢材之间摩擦系数取0.45。螺栓模型和管片接头有限元分析模型如图9所示。
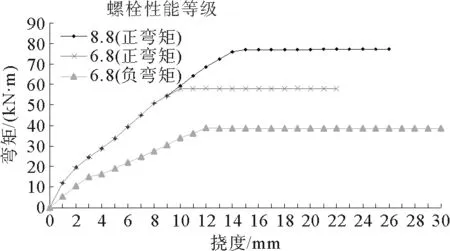
图10 不同管片接头的挠度-弯矩曲线Fig.10 Deflection-bending moment curve of different segment joints
2.2 管片接头承载力有限元模拟计算结果分析
对管片接头在无轴力情况下的极限承载力进行分析。将上述模型按照混凝土管片同样的加载方式,通过位移加载得到管片接头的极限承载力。对带有两种性能等级的螺栓的管片接头进行模拟分析,得到正弯矩作用下极限状态下管片接头中钢筋和螺栓的受力情况。模拟发现,管片接头内部纵筋和箍筋并未达到极限状态,而最大应力出现在螺栓处,说明管片接头处的弯矩主要由接头处螺栓来承担。正弯矩作用下两种管片接头的极限弯矩分别为77和58 kN·m,再对带有性能等级为6.8螺栓的管片接头,在负弯矩作用下进行模拟分析,得到管片接头的极限弯矩为38 kN·m。管片接头的挠度-弯矩曲线如图10所示。对带有性能等级8.8螺栓的管片,观察其正弯矩作用下的挠度-弯矩曲线,可以发现当管片接头加载面挠度达到13 mm时螺栓开始屈服,随着荷载的增加,螺栓进入塑性变形阶段,管片接头上部受压区面积逐渐减小。螺栓屈服后,在弯矩不变的情况下,挠度持续增加,直至螺栓达到极限应变,管片接头也达到极限承载力。
此外值得注意的是,在对正弯矩作用下带有性能等级8.8螺栓的管片接头各个构件产生的应变分析中发现,在极限荷载条件下混凝土最大压应力出现在管片接头手孔面与螺帽接触处(图11)。手孔面与螺帽接触处混凝土最大应变随加载变化如图12所示。可以推断,在加载过程中螺帽对手孔面造成极大的压应力,并且在弯曲过程中螺杆和螺栓孔产生挤压也会导致混凝土破坏。若提高螺栓强度或混凝土的强度不足时,将极易导致手孔和螺栓孔处的混凝土过早破坏。说明在管片接头的设计中要充分考虑螺栓和混凝土的强度配比,防止手孔和螺栓孔处集中应力过大所造成的混凝土破坏。
管片接头的极限承载能力主要由螺孔处混凝土的强度和接头处螺栓的极限承载力所决定。通过与完整混凝土管片极限弯矩的对比可以看出,管片接头的存在对盾构管片的极限承载能力有很大的折减。如表3所示,通过对比正负弯矩作用下管片接头的极限弯矩,可以发现管片接头的极限弯矩与螺栓的位置有关。
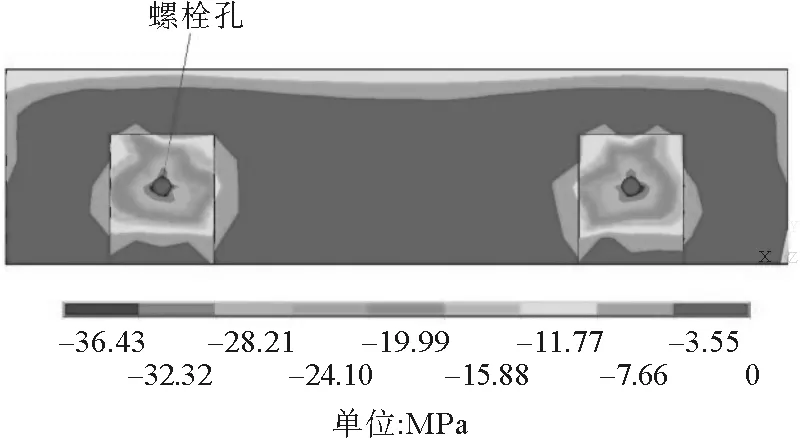
图11 管片接头手孔面与螺帽接触处混凝土压应力图Fig.11 Compressive stress distribution on concrete in contact position between hand hole surface and bolt nut

图12 管片接头手孔面与螺帽接触处混凝土挠度-应变曲线Fig.12 Deflection-strain curve of concrete in contact position of hand hole surface and bolt nut

表3 管片接头极限弯矩Tab.3 Ultimate bending moment of segment joint
3 结论
1) 采用对称布筋的混凝土管片,利用有限元模拟不同轴力作用下管片的极限承载力特性。研究发现,整体管片的极限弯矩随着轴力的增加而提高,且近似成线性变化,最大轴力时的极限承载力相对于无轴力情况增加约70%。
2) 通过对管片接头的有限元模拟发现,管片接头处的极限承载力主要与螺栓强度和位置有关,且极限承载力随螺栓强度的增加而增加。管片接头的极限承载力与完整管片的极限承载力相比有很大的降低,正弯矩作用下带有性能等级8.8螺栓的管片接头极限弯矩是整体管片极限弯矩的40%,带有性能等级6.8螺栓的管片接头极限弯矩是整体管片极限弯矩的30%。而相同性能等级螺栓的管片接头,其负弯矩作用下的极限弯矩是正弯矩作用下的60%。
3) 通过查看混凝土的开裂情况发现,由于螺栓强度远大于混凝土强度,在管片接头手孔与螺帽接触处的混凝土受应力集中较为严重,极易造成该区域的混凝土在加载过程中过早破坏。因此,在管片设计过程中要充分考虑该区域混凝土的强度。
[1]HUANG X,HUANG H W,ZHANG J.Flattening of jointed shield-driven tunnel induced by longitudinal differential settlements[J].Tunnelling and Underground Space Technology,2012,31(9):20-32.
[2]LI X J,YAN Z G,WANG Z,et al.Experimental and analytical study on longitudinal joint opening of concrete segmental lining[J].Tunnelling and Underground Space Technology,2015,46(5):52-63.
[3]张厚美,张正林,王建华.盾构隧道装配式管片接头三维有限元分析[J].上海交通大学学报,2003,37(4):566-569. ZHANG Houmei,ZHANG Zhenglin,WANG Jianhua.3-D FEM analysis on prefabricated segment joints of shield tunnel[J].Journal of Shanghai Jiaotong University,2003,37(4):566-569.
[4]葛世平,谢东武,丁文其.盾构管片接头简化数值模拟方法[J].岩土工程学报,2013,35(9):1600-1605. GE Shiping,XIE Dongwu,DING Wenqi.Simplified numerical simulation method for segment joints of shield tunnels[J].Chinese Journal of Geotechnical Engineering,2013,35(9):1600-1605.
[5]俞涛,何川,曾东洋.地铁盾构隧道管片接头的三维有限元分析[J].市政技术,2004,22(增):168-171. YU Tao,HE Chuan,ZENG Dongyang.Analysis of 3D FEM on segment joint of metro shield tunnel[J].Municipal Engineering Technology,2004,22(S):168-171.
[6]ARNAU O,MOLINS C.Three dimensional structural response of segmental tunnel linings[J].Engineering Structures,2012,44:210-221.
[7]BLOM C B M,HORST E J,JOVANOVIC P S.Three-dimensional structural analyses of the shield-driven “green heart” tunnel of the high-speed line south[J].Tunnelling and Underground Space Technology,1999,14(2):217-224.
[8]CHEN J S,MO H H.Numerical study on crack problems in segments of shield tunnel using finite element method[J].Tunnelling and Underground Space Technology,2009,24:91-102.
[9]MOLINS C,ARNAU O.Experimental and analytical study of the structural response of segmental tunnel linings based on an in situ loading test.Part 1:Test configuration and execution[J].Tunnelling and Underground Space Technology,2011,41(6):764-777.
[10]GONG W P,JUANG C H,HUANG H W,et al.Improved analytical model for circumferential behavior of jointed shield tunnels considering the longitudinal differential settlement[J].Tunnelling and Underground Space Technology,2015,45(1):153-165.
[11]YANG Y Z,ZHANG W W,WANG J W.Three-dimensional orthotropic equivalent modelling method of large-scale circular jointed lining[J].Tunnelling and Underground Space Technology,2014,44(1):33-41.
[12]周海鹰,李立新,陈廷国.地铁隧道衬砌管片承载力试验及计算方法[J].山东大学学报(工学版),2010,40(4):84-87. ZHOU Haiying,LI Lixin,CHEN Tingguo.Experiments and calculation method for bearing capacity of the lining segment of metro shield tunneling[J].Journal of Shandong University (Engineering Science),2010,40(4):84-87.
[13]陈仁东.北京地铁四号线管片配筋设计与优化[J].现代隧道技术,2006,43(5):50-54. CHEN Rendong.Optimum design for the reinforcement of the lining segments in Beijing metro line 4[J].Modern Tunnelling Technology,2006,43(5):50-54.
[14]中华人民共和国国家标准.GB 50010—2010,混凝土结构设计规范[S].
[15]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005:221-222.
(责任编辑:吕海亮)
Numerical Simulations for Ultimate Bearing Capacities of Concrete Segments and Its Joints
LI Shouju1, LI Yutao1, SHANGGUAN Zichang2, YU Shen1
(1. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, Liaoning 116024, China;2. Institute of Marine and Civil Engineering, Dalian Ocean University, Dalian, Liaoning 116023, China)
In order to analyze the mechanical characteristics of reinforced concrete segments and its joints, finite element method (FEM) was used to simulate the bearing capacities of concrete segments and its joints. The constitutive relations of concrete was simulated with second-degree parabola and straight line model proposed by Rush. Elastic-perfect plastic constitutive model was applied in modeling constitutive relations of reinforcement bars. Link elements in ANSYS software were used to simulate the longitudinal reinforcement and stirrup bars inside concrete segments and segment joint bolts. The ultimate bearing capacity of concrete segments was studied under the action of bending moment with different axial forces. The bearing capacities of concrete segment joints were also studied under the action of the positive and negative bending moments. The study shows that the ultimate bending moment of concrete segments increases with the increase of the axial force and that the ultimate bending moments of segments with maximum axial force is increased by 70% compared with the ultimate bearing capacity of segments without axial force. The study on segment joints shows that the ultimate bearing capacity of segment joints is only about 40% of that of concrete segments, that the existence of joints greatly reduces the bearing capacities of the concrete segments, and that the ultimate bending moment of segment joints is mainly controlled by the strength and position of joint bolts.
concrete segment; segment joint; loading capacity; numerical simulation; ultimate bending moment; fracture process
2016-01-14
国家重点基础研究发展计划(“973”)项目(2015CB057804);国家自然科学基金项目(11572079);工业装备结构分析国家重点实验室开放基金项目(S14206)
李守巨(1960—),男,辽宁辽中人,教授,博士,主要从事岩石力学与混凝土结构研究.E-mail: lishouju@dlut.edu.cn
U451+.4
A
1672-3767(2017)01-0072-06

