1-Norm/2-Norm约束及小波多尺度2D体波走时成像
高 级,方洪健
(中国科学技术大学 地球和空间科学学院地震与地球内部物理实验室,合肥 230026)
1-Norm/2-Norm约束及小波多尺度2D体波走时成像
高 级,方洪健
(中国科学技术大学 地球和空间科学学院地震与地球内部物理实验室,合肥 230026)
在对浅地表复杂地下介质层析成像时,由于观测系统局限性及方法本身对特定岩石地球物理属性的不敏感性等因素,造成地球物理反演存在多解性。在地震走时成像中,地震射线数量在低速区域分布较少形成阴影区,造成其对低速区域成像分辨率较低。同时因为观测数据包含干扰信息以及不同反演方法的局限性等因素造成反演结果包含次生假异常。这里主要研究了空间域的L1-norm、L2-norm约束反演及小波域小波系数稀疏约束反演,对比不同反演方式及约束条件对地质模型的分辨能力。通过测试孤立异常模型、层状地层模型、倾斜地层模型,得出三种不同反演方式分别具有对不同特定模型的分辨特性。在实际资料成像中,可以通过使用多种反演方式,对比反演结果合理性以期达到更准确的地质构造解释。
体波走时; 层析成像; 1-Norm; 2-Norm; 小波多尺度
0 引言
地震初至走时层析成像就是用地震数据来反演地下结构的物质属性,并逐层剖析绘制其图像的技术,其主要目的是确定地球内部的精细结构和局部不均匀性[1]。
地震层析成像主要包括:①模型的参数化;②正演计算地下介质属性的理论值;③反演及图像重建;④反演结果的评价[2]。
模型参数化可分为两类:①不分块参数化,反演在泛函空间中进行,理论上可以计算任意位置的速度,结果不受离散化的影响,但其计算量较大,不利于实际利用;②离散化的模型参数化,其优点是数学上容易处理,运算相对简单,缺点是在一般方法中出现的某些简化,在用离散时可能被掩盖掉。现在通用的大都是离散化的模型参数化,通常采用分块网格或节点法。
分块法将模型按某种准则划分为块体,假定每块内速度是常值。分块法在进行射线追踪和走时计算时简便,但是在模型中人为的引入了块体间的边界,造成了速度的不连续性,并且结构异常的轮廓只能表示成块状;节点法则是把节点上的速度值取为待求变量,其他任意点的速度值由于它相邻的8个节点上的速度插值求得。与分块法相比,节点法速度是连续变化的,没有人为的边界,可以获得系数矩阵更密,节点法只能处理速度连续变化的情况,但无法处理存在速度间断面的情况。
在实际工程勘探中,如地铁施工中遇到的孤石、煤矿工作面中陷落柱、断层等构造异常情况,均匀地质背景下会遇到速度突变的地质问题。节点法在连续背景速度情况下对速度突变界面分辨率降低的情况,反演结果存在对初始模型依赖性强、易陷入局部极值等问题。在地震信号处理中,稀疏表示地震数据一直是近些年来发展的一个热点问题[3-4],采用尽可能少的非零元素表示信号的主要信息,从而简化在地震信号处理中的求解过程[5-6]。
小波分析多尺度分解反演方法,将参数反演问题转化到小波域中重要系数求解问题。利用多尺度之间的内在联系及小波域中小波系数的稀疏性,有效改进了局部极值、计算量等问题[7-8]。多尺度反演往往从较粗尺度开始,由于较粗尺度下目标函数呈现较强的凸性及较少的局部极值,有利于收敛至全局优化解。进而有学者将小波变换为基础的多尺度分析理论应用于规则格点或方块的模型参数化中[9-12],并在反演过程中根据数据的分辨极限自动对模型进行多尺度再划分。这种方法起到了不规则划分网格的作用,先在粗尺度上迭代反演,得到一个比较好地参数估计,再将这个估计作为较小尺度的初始速度进行反演,直到反演出原问题的全局最优解。其优点是对初始模型选择依赖性减小、更适合于大扰动异常体成像、图像分辨率和质量较高。
针对稀疏方程L0范数(向量中非零元素个数)约束最小二乘解,但L0范数约束时方程求解为非凸函数求解,其解容易陷入局部极小值[13]。L1范数约束为L0与L2范数约束之间的一种折中且可行的方法,且L1范数约束时方程为凸函数求解,方程可求出全局最优解。采用加权迭代最小二乘IRLS (Iteratively Reweighted Least Squares) 求解此类稀疏方程[14-16],若求解模型尺度较大,则可使用迭代收缩算法ISA(Iterated Shrinkage Algorithms)[17-18]。
这里首先采用双线性插值节点法离散速度模型;其次采用MSFM(Multi-Stencils Fast Marching Methods)正演计算走时场,并采用龙格库塔方法求取路径梯度求解最短射线路径。在对速度结构成像时,着重比较了L1全变差约束、L2范数约束、小波域多尺度稀疏约束,对比分析不同约束反演对不同模型分辨能力,指导实际地质背景下的速度成像,为实际地质问题提供更合理的解释。
1 方法
1.1 地震走时方程建立
地震初值走时成像为通过射线的传播时间来拟合地下介质速度结构的一种成像方法。在二维情况下,观测地震初值到时可以表示为:
(1)
式中:Ti为第i条射线观测到时;v(x,z)与s(x,z)为地下某一点处介质速度慢度值;Γi为第i条射线路径。
在做速度成像时,需要把速度模型离散成独立的网格[19],此时式(1)离散并写成矩阵形式,见式(2)。
d=Gm
(2)
式中:d为观测数据(N×1,N射线路径数);m为慢度(M×1,M为模型网格数),G为灵敏度矩阵(N×M),即G的每一行为观测数据对应行对所有模型变量的偏导数。
若求解模型的最小长度,解为式(3)。
m=(GTG)-1GTd
(3)
1.2 模型与灵敏度矩阵的小波分解
小波是定义在有限间隔而且其平均值为零的一种函数,小波变换是信号f(t)与被缩放和平移的小波函数之积在信号存在的整个期间里求和,小波变换完成之后得到的系数是在不同的缩放因子下由信号的不同部分产生的。
对于连续小波变换,将任意L2(R)空间的函数f(t)在小波基下展开,成为函数的小波变换(小波分解),其表达式为[20]:
WTf(a,τ)=
(4)
若小波变换满足容许条件,则其逆变为式(5)。
(5)
这里在对模型与灵敏度矩阵做小波分解时,选择了Haar与Db2小波基。
1.3 小波域走时方程建立与求解
地震走时小波域多尺度反演成像步骤为,在建立灵敏度矩阵时采用基于Haar、Db2小波基的二维小波分解把灵敏度矩阵变换到小波域中,把在时域中求解速度模型的问题转化到稀疏的多尺度小波系数的求取,并采用迭代过程中变权重法(IRLS)求解小波系数;最后采用小波逆变换把求解出的小波系数变量,变换到时域中的慢度更新量以达到对地下介质速度结构成像。
对于正交小波变换,有W-1=WT,WTW=I,I表示单位矩阵,式(2)可以写为[7、14]:
Δd=GWTWΔm
(6)


(7)
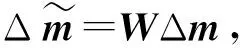

1.4 二阶吉洪诺夫与全变差正则化约束
井间地震波走时层析成像采用在孔中观测的方式重建井间地层的速度结构,因为我们需要根据孔中的观测到时求解速度沿横向与纵向的变化情况,导致式(2)严重欠定、条件数较大。必须采用正则化的方式减小解的假异常与不适定问题,一般情况下,为了权衡求解的稳定性及假异常采用吉洪诺夫正则化与拉普拉斯变换约束。这两种约束方法均为二范数约束。二范数约束目标函数为:
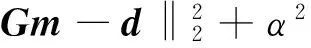
(8)
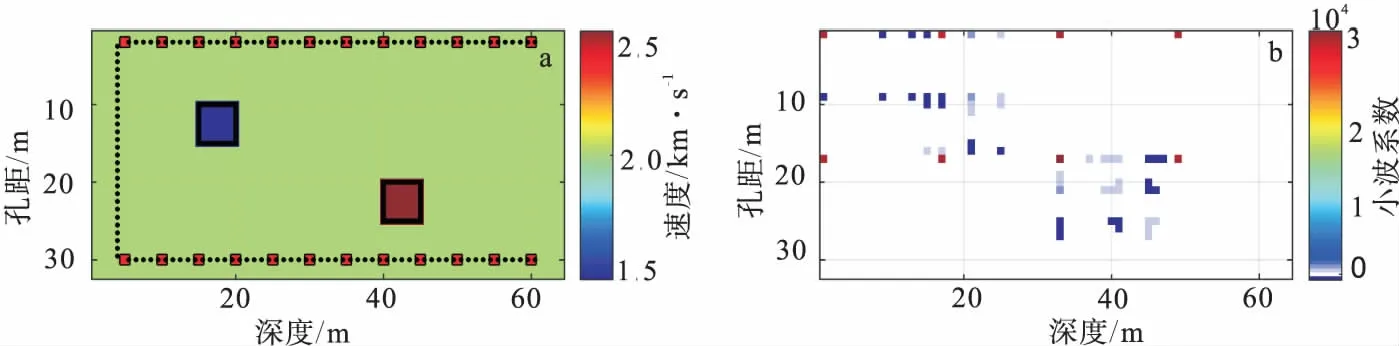
即折中模型平滑与因干扰异常产生的假异常,加上平滑约束参数相当于对模型求解方程增加了低通滤波器,使求解结果损失部分高频信息,同时模糊了突变异常体的边界,造成反演结果分辨率降低。随着二范数(L2-norm)的广泛应用,最近开展了比较多的对Lp-norm约束的研究(0 (9) 在具体求解式(7)时,对其求导并令其一阶导数为零可得[23]: (2GTG+αLTWL)m=2GTd (10) 式(8)写成矩阵形式为: (11) 采用IRLS迭代方式求解方程(11),每次迭代分别重新计算W平滑权重系数[23]。 我们设计了一个井-井观测系统,模拟工程中经常遇到的孤石或者溶洞情况。如图1所示,孔距28 m、背景速度2 000 m/s,模型大小为32×64 m共计2 048个网格,两个异常边长为5 m×5 m,速度分别2 500 m/s、1 500 m/s。分别模拟充水充泥的低速溶洞与高速的孤石异常。从图1中可以看出,速度模型变换到小波域中模型极为稀疏,2 048个小波系数中零值数目为1 937个,非零值111。即如果直接反演速度模型需要反演2 048个速度值,而在小波域中反演只需要反演111个小波系数值既可以完全恢复速度模型,使反演的目标模型较为稀疏。针对此种稀疏反演,这里采用IRLS求解稀疏模型方程,在迭代过程中动态选择权重系数。 图1 速度模型与其对应的2阶Haar小波系数Fig.1 Cross-borehole configuration and the 2rd Haar-Wavelet coefficient(a)速度模型;(b)速度模型的二阶Haar小波变换后的小波系数 2.1 基于MSFM走时场计算 首先采用MSFM(Multi-Stencils Fast Marching Methods) 求解程函方程,正演计算初至到时。多模板快速推进算法是一种 FMM(Fast Marching Method) 的改进算法。该算法使用两个模板分别用二阶差分近似计算水平垂直方向以及对角线方向上网格节点的波前传播时间,并选取满足逆风条件的解,从而大大提高了 FMM 算法的计算精度和计算效率[24]。图2为MSFM求解的波前走时场、反演迭代过程中射线路径分布。 图2 地震波波场与射线路径Fig.2 Seismic time field and ray path(a)MSFM追踪地震波走时场;(b)迭代过程中射线路径 2.2 孤立异常模型 图1中所示两个孤立高低速异常,对应于工程地质中孤石或煤矿工作面溶洞构造,其中高速对应孤石,低速对应溶洞。在具体求解过程中,采用四种反演策略,分别为在空间域中采用全变差L1-norm与二阶吉洪诺夫正则化求解速度模型、小波域全变差求解基于Haar与Db2小波基的小波系数然后通过小波逆变换求解模型速度。初始速度模型均给定背景速度2 000 m/s。 图3为不同约束条件下的速度模型反演结果。从反演结果可以看出,全变差约束与二阶吉洪诺夫约束具有较为平滑的反演结果,为达到反演结果稳定均产生了一定的假异常,但全变差约束具有更好的模型恢复及更少的假异常,对低速异常具有更好的分辨能力;基于Haar与Db2小波基的小波域反演比时空域反演具有更为干净的背景,以及较少的干扰异常,但基于Haar小波基的反演产生了一定的拖尾异常,以及异常边界过于尖锐,造成此情况的原因为Haar小波基为一个方波形态,过渡太迅速,高频成分较多,针对此情况我们首先采取加大阻尼和平滑的权重,随着权重的加大能一定程度压制Haar小波的高频成分,但也造成了对低速区域无法分辨的缺陷。从图3(d)可以看出,一个方面减少了均匀背景上假异常的情况,同时具有较好的异常边界分辨率。 图3 地震波走时正反演Fig.3 Seismic travel time tomography inversion results(a) 全变差反演结果;(b) 吉洪诺夫二阶正则化反演结果;(c) Haar小波域反演结果;(b) Db2小波域反演结果 图4为不同约束条件下迭代残差曲线图,从图4中可以看出,开始迭代时基于Haar小波基的反演具有最小的拟合误差,二阶吉洪诺夫具有最大的拟合误差,随着迭代次数的增加,4种不同的约束具有大致相同的拟合误差,说明4种方式反演均具有随着迭代次数增加拟合误差减小及稳定的收敛趋势。同时也说明了在相同拟合误差的情况下存在多种反演结果,即反演的不唯一性。 2.3 垂直与水平地层模型 图5、图6分别为竖直层状与水平层状速度模型反演结果,从图5、图6中可以看出,L1范数全变差与L2吉洪诺夫正则化约束下均具有较为平滑的结果,且全变差反演结果具有更少的假异常;小波域中反演的结果具有较好的边界刻画能力,其中基于Harr小波基的反演几乎精确恢复速度模型,基于Db2小波基反演在异常边界处也具有走向一致性。从反演结果数值恢复与边界刻画来看,空间域反演具有更好的数值恢复,小波域反演具有更好的边界刻画。 图4 不同约束条件下迭代残差曲线图Fig.4 Iterative residual curves uneler different constraint conditions 图5 竖直层状模型反演Fig.5 Vertical layered velocity model(a)观测系统;(b)速度模型;(c)全变差约束;(d)二阶Tikhonov正则化约束;(e)稀疏约束-Haar小波基;(f)稀疏约束-Db2小波基 图6 水平层状模型反演Fig.6 Horizontal layered velocity model(a)观测系统;(b)速度模型;(c)全变差约束;(d)二阶Tikhonov正则化约束;(e)稀疏约束-Haar小波基;(f)稀疏约束-Db2小波基 2.4 倾斜断层模型 图7为倾斜断层速度模型反演结果,从图7中可以看出,L1范数全变差与L2吉洪诺夫正则化约束下均具有较为平滑的结果,边界控制相对模糊,其中L1约束出现局部极值高速区域没有L2约束下背景速度恢复的均匀平滑;针对倾斜速度结构模型,小波域反演效果没有孤立异常与层状模型边界刻画的好,其反演结果均带有一定的锯齿状形态存在,同时基于Db2小波基反演比基于Haar小波基具有更好的背景平滑度。 图7 倾斜断层模型反演Fig.7 Slope fault velocity modela)观测系统;(b)速度模型;(c)全变差约束;(d)二阶Tikhonov正则化约束;(e)稀疏约束-Haar小波基;(f)稀疏约束-Db2小波基 在井-井地震走时层析成像反演的基础上,讨论了小波域多尺度反演与空间域L1-norm、L2-norm约束反演下,对不同模型结构的分辨能力,取得了以下几点的认识: 1)对于块状速度结构,在空间域欠定的迭代方程在小波域具有更好的完备性及稳定性。 2)全变差L1-norm约束与二阶L2-norm吉洪诺夫约束相比反演结果具有更少的假异常,在对孤立异常反演时,全变差约束具有更好的边界识别及低速区域数值恢复。 3)针对层状地层模型,基于Haar小波基的多尺度约束下成像具有准确的边界分辨力。 4)L2-norm约束对不同速度结构模型具有折中的成像效果。 5)针对不同的地质模型,不同反演方法分别具有优缺点,在对实际地质资料反演成像时,因预先不知道地层结构,一个推荐的方法为采用多种反演约束方法分别反演,对比之间的区别,综合推断一个更为合理的地层结构解释。 [1]杨文采,李幼铭.应用地震层析成像[M].北京:地质出版社,1993.YANG W C,LI Y M.Application of seismic tomography [M].Beijing:Geological publishing house,1993.(In Chinese) [2]雷栋,胡祥云.地震层析成像方法综述[J].地震研究,2006.29(4):418-425.LEI D,HU X Y.Seismic tomography methods review [J].seismic study,2006.29(4):418-425.(In Chinese) [3]YUAN S,WANG S.Spectral sparse Bayesian learning reflectivity inversion[J].Geophysical Prospecting,2013,61(4):735-746. [4]YUAN S,WANG S,LUO C,et al.Simultaneous multitrace impedance inversion with transform-domain sparsity promotion[J].Geophysics,2015,80(2):R71-R80. [5]BRUCKSTEIN A M,DONOHO D L,ELAD M.From sparse solutions of systems of equations to sparse modeling of signals and images[J].SIAM review,2009,51(1):34-81. [6]冯飞.结合稀疏变换的稀疏约束反演一次波估计研究[D].长春:吉林大学,2014.FENG F.Combined with a wave of sparse constraint inversion of the sparse transform estimation research [D].Changchun:Jilin University,2014.(In Chinese) [7]马坚伟,杨慧珠.地震波形多尺度反演的一点讨论[J].地球物理学进展,2000,15(4):55-61.MA J W,YANG H Z.Multi-scale inversion of seismic waveform is discussed [J].Progress in Geophysics,2000,15(4):55-61.(In Chinese) [8]马坚伟,朱亚平,杨慧珠.二维地震波形小波多尺度反演[J].工程数学学报,2004,21(1):109-113.MA J W,ZHU Y P,YANG H Z.Two-dimensional wavelet multiscale seismic waveform inversion[J].Chinese Journal of Engineering Mathematics,2004,21(1):109-113.(In Chinese) [9]裴正林,牟永光.复杂介质小波多尺度井间地震层析成像方法研究[J].地球物理学报,2003,46(1):113-117.PEI Z L,MOU Y G.Complex medium wavelet multi-scale method of crosshole seismic tomography study[J].Chinese Journal of Geophysics,2003,46(1):113-117.(In Chinese) [10]宋常瑜,裴正林,狄帮让,等.小波多尺度井间地震衰减层析成像[J].石油地球物理勘探,2007,42(1):30-33.SONG C Y,PEI Z L,DI B R,et al.The wavelet multi-scale cross-hole seismic attenuation tomography[J].Geophysical prospecting for petroleum,2007,42(1):30-33.(In Chinese) [11]NAZZAL,M.,& OZKARAMANLI,H.Wavelet domain dictionary learning-based single image superresolution.Signal,Image and Video Processing,2015,9(7):1491-1501. [12]TIKHOTSKY,S.,& ACHAUER,U.Active Seismic Tomography Inversion with the Self Adaptive Wavelet Parameterization:Algorithm and its Application for the Vesuvius Volcano Structure[C].In Proc.7th Int.Conf.on Problems of Geocosmos,St.Petersburg,Russia ,2008:251-252. [13] BRUCKSTEIN A M,DONOHO D L,ELAD M.From sparse solutions of systems of equations to sparse modeling of signals and images[J].SIAM review,2009,51(1):34-81. [14]KARLOVITZ L A.Construction of nearest points in the L p,p even,and L∞ norms[J].Journal of Approximation Theory,1970,3(2):123-127. [15]RAO B D,ENGAN K,COTTER S F,et al.Subset selection in noise based on diversity measure minimization[J].Signal Processing,IEEE Transactions on,2003,51(3):760-770. [16]FANG H,ZHANG H.Wavelet-based double-difference seismic tomography with sparsity regularization[J].Geophysical Journal International,2014,199(2):944-955. [17]KOLACZYK E D.A wavelet shrinkage approach to tomographic image reconstruction[J].Journal of the American Statistical Association,1996,91(435):1079-1090. [18]FIGUEIREDO M A T,NOWAK R D.An EM algorithm for wavelet-based image restoration[J].Image Processing,IEEE Transactions on,2003,12(8):906-916. [19]AKI K,LEE W H K.Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes:1.A homogeneous initial model[J].Journal of Geophysical research,1976,81(23):4381-4399. [20]郝金来,姚振兴.小波域反演确定区域地震震源机制[J].中国科学地球科学 (中文版),2012,42(2):191-201.HAO J L,YAO Z X.The wavelet domain inversion to determine the regional earthquake focal mechanism [J].Chinese science and earth sciences,2012,42(2):191-201.(In Chinese) [21]BEHROOZ A,ZHOU H M,EFTEKHAR A A,et al.Total variation regularization for 3D reconstruction in fluorescence tomography:experimental phantom studies[J].Applied optics,2012,51(34):8216-8227. [22]YUAN S,WANG S,LI G.Random noise reduction using Bayesian inversion[J].Journal of Geophysics and Engineering,2012,9(1):60-68. [23]ASTER R C,BORCHERS B,THURBER C H.Parameter estimation and inverse problems[M].Academic Press,2011. [24]王飞,曲昕馨,刘四新,等.一种新的基于多模板快速推进算法和最速下降法的射线追踪方法[J].石油地球物理勘探,2014,49(6):1106-1114.WANG F,QU X X,LIU S X,et al..A new rapid advance algorithm based on template and the steepest descent method of ray tracing method [J].Geophysical prospecting for petroleum,2014,49(6):1106-1114.(In Chinese) Compared 1-Norm / 2-Norm constraint and wavelet multi-scale 2D body wave velocity tomography GAO Ji,FANG Hong-jian (Laboratory of Seismology and Physics of Earth's Interior,University of Science and Technology of China,Hefei 230026,China) Because of the limited coverage of observation system and the complex physical relationship between physical parameters and observations,near surface geophysical method suffers issues of non-uniqueness and resolution limitation to some degree.For seismic travel time tomography,number distribution of ray paths in low speed region is less than the high speed region,and this phenomenon leading to the seismic travel time tomography have a low resolution for low speed region.At the same time,the measured data affected by many complicated environmental factors usually include strong noises and the limitations of different inversion method,which badly force the inversion result contain artifacts.We main studied tomography with different constraints of spatial domain of L1 norm,L2 norm and wavelet coefficients of wavelet domain.Compared the different inversion methods and constraint conditions on the resolution of geological model.Through test isolated anomaly model,layered stratum model,tilted strata model,three different inversion methods of different specific model distinguish characteristics respectively.In the actual data imaging,can through the use of multiple inversion methods,compare the inversion result rationality in order to achieve more accurate geological structure interpretation. body wave travel time; tomography; 1-Norm; 2-Norm; wavelet multi-scale 2015-10-20 改回日期:2015-10-26 国家自然科学基金项目(41474039) 高级(1983-),男,博士,主要从事地震资料处理,弹性波层析成像、电阻率层析成像、多属性联合反演研究,E-mail:gaoji617@mail.ustc.edu.cn。 1001-1749(2016)06-0765-08 P 631.4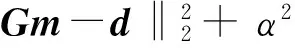

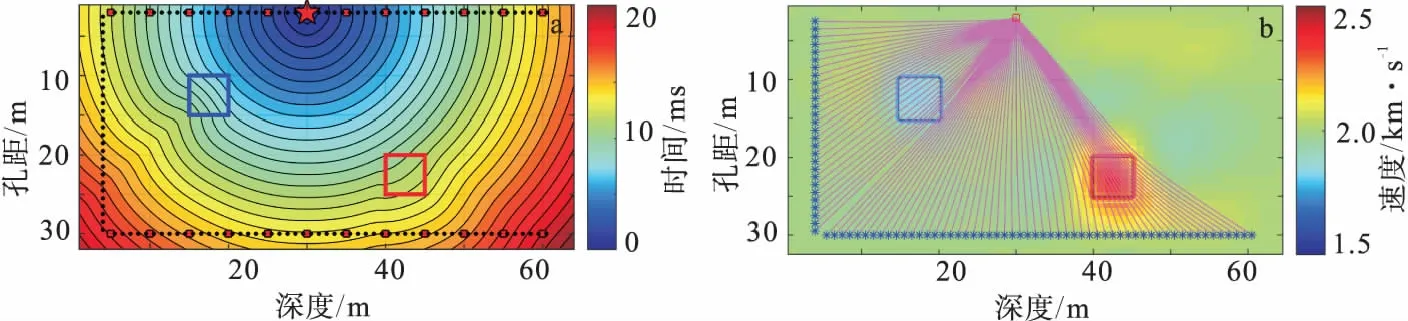
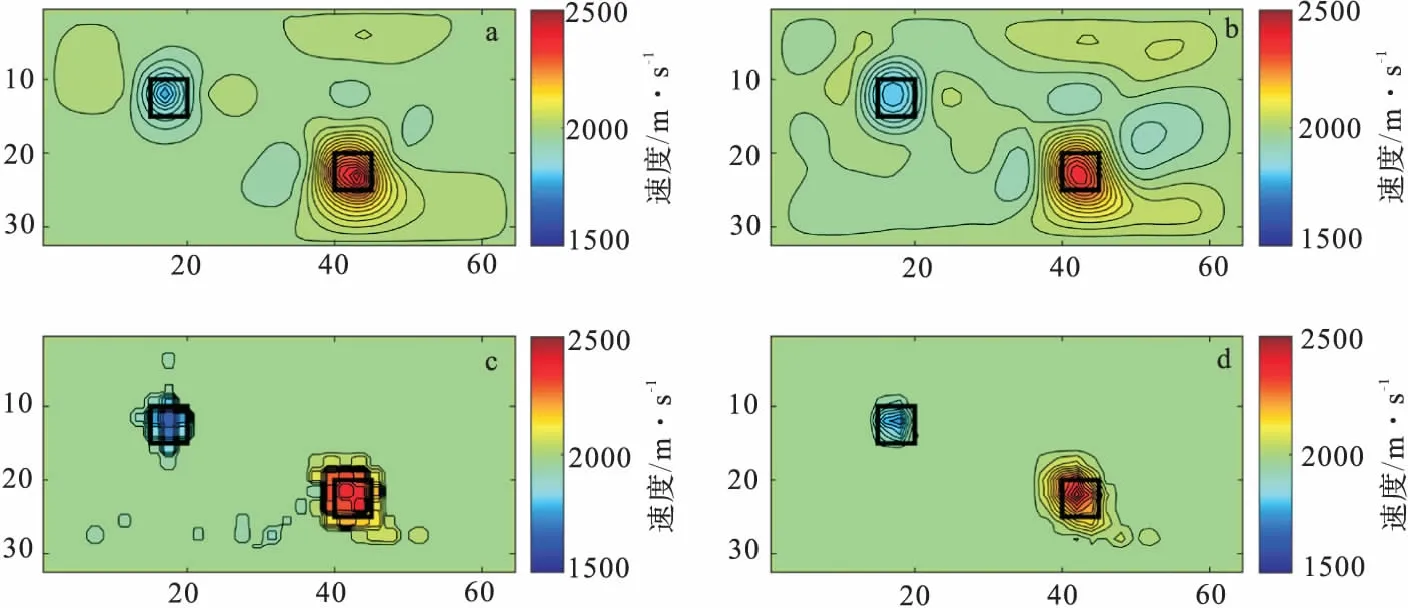
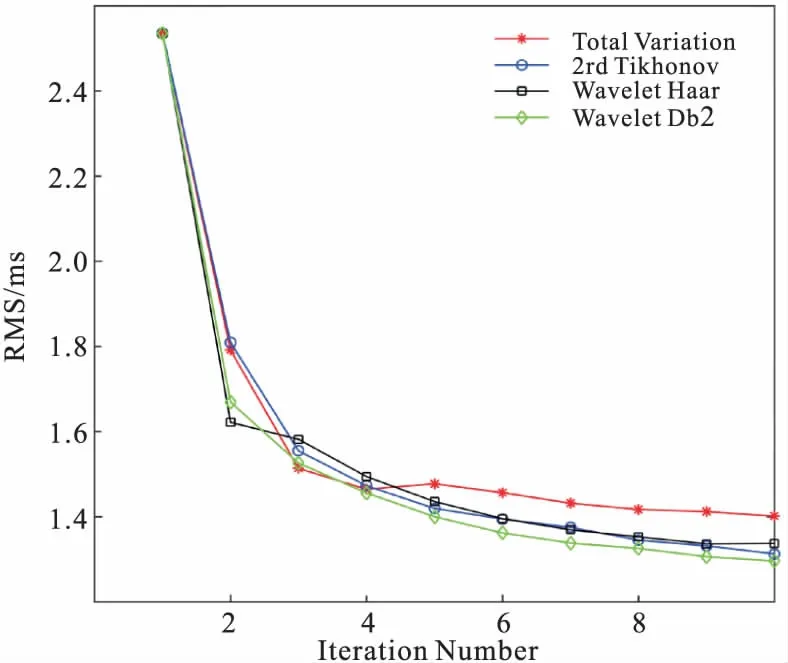
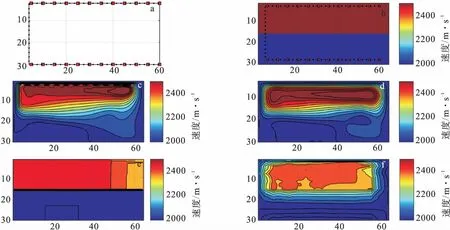
2 合成数据测试

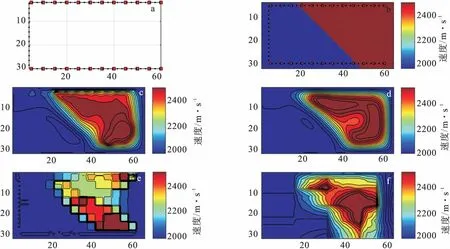
3 结论与讨论

