基于振幅谱能量误差最小原则的品质因子提取方法研究与应用

孙文国,曹丹平,冯吉浩

(中国石油大学(华东)，青岛 266580)

基于振幅谱能量误差最小原则的品质因子提取方法研究与应用

孙文国,曹丹平*,冯吉浩

(中国石油大学(华东)，青岛 266580)

品质因子Q是衡量地震波传播过程中能量衰减的重要参数，对含油气储层识别和地震波衰减补偿具有重要意义。谱比法是实际资料处理中最常用的方法之一，但容易受到时窗、频带范围选取等人为因素的影响，使品质因子反演结果存在不稳定性。这里提出基于振幅谱能量误差最小原则的品质因子提取方法，该方法充分利用整个频带范围内振幅谱的信息，通过构建衰减前、后振幅谱能量随Q变化的目标函数估算品质因子，有效地解决了频谱直接相除和频带拟合区间选取等引起的影响。零偏VSP模型测试表明，基于振幅谱能量误差最小原则的品质因子提取方法比谱比法具有更高的精度，并在实际资料应用中取得了较好的效果。

品质因子； VSP； 振幅谱能量； 指数法； 谱比法

0 引言

地震波在地下介质的传播过程中，由于受到地层吸收衰减作用的影响，能量会发生衰减，造成的因素主要分为两类：①非固有衰减；②固有衰减。其中固有衰减反映了介质的非弹性性质，通常用品质因子Q来度量。Futterman[1]第一次把地层的吸收衰减作用表述成地层的基本属性。自此以后，针对地层的吸收参数的计算，特别对Q值的计算得到了较大地发展。品质因子估算方法主要分为三大类：①时间域方法，包括振幅衰减法[2]、子波模拟法[3]、上升时间法[4]和解析信号法[5]等；②频率域方法主要包括谱比法[6]、质心频率偏移法[7]和峰值频率偏移法[8]等；③方法在时频域实现，主要有小波域能量衰减法[9]和基于小波变换的叠前地震资料估计品质因子[10]等。研究表明，没有一种方法具有普遍适用性，反演结果都依赖于地震资料的质量[11-12]。频率域方法利用多点信息反演Q值，比时间域方法具有更高的抗噪性、稳定性。

Bath M[6]首次提出了谱比法，并指出谱比法中频谱比的斜率是Q的函数。在此基础上，YihJeng[13]假设Q值与频率相关，实现了从多波地震资料、CMP道集计算品质因子；张大伟等[14]利用零偏VSP资料进行反演，对比了谱比法和质心频移法，结果显示质心频率频移法比谱比法更精确；E.Blias[15]通过构建目标函数的方法提出了利用VSP下行波计算Q值的改进的谱比法；曹思远[16]将质心频率偏移法与谱比法优点相结合，根据子波振幅对数谱上的衰减规律，提出了一种基于对数谱统计量组合的Q值反演方法。但是常规谱比法及其改进的方法仍然需要通过在指定频带范围内，通过振幅谱相比来提取Q值。如何充分利用整个有效频谱信息，减小振幅谱直接相除引起的不确定性与不稳定性的问题，是品质因子提取过程中的焦点。

笔者根据衰减前、后振幅谱能量的差异，将Q作为反演参数，构建衰减前后振幅谱能量随品质因子变化的目标函数。在整个频带范围内，通过满足目标函数最小反演出地层最佳品质因子。

1 基本原理

1.1 谱比法

谱比法是频率域中最常用的一种方法，它假设Q值与频率无关，通过拟合振幅谱对数比随频率的变化斜率，估算品质因子Q。S1(f)为衰减前地震波振幅谱，根据吸收衰减理论，地震波在吸收介质中传播t时间后其振幅谱S2(f)可以表示为：

(1)

式中：t为地震波衰减前后的单程旅行时；Q为地层的等效品质因子；系数C是与衰减和频率无关的衰减项(包括反射、投射、几何扩散等因素)。

建立振幅谱比值的对数随频率变化的线性关系：

(2)

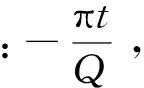
1.2 品质因子估算方法

针对谱比法频谱相除和频谱拟合区间选取所引起的不稳定性，提出基于振幅谱能量误差最小原则的品质因子提取方法。该方法在谱比法基础上，根据式(2)构建关于品质因子的目标函数，通过目标函数最小反演最佳品质因子：

(3)

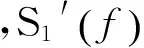
(4)

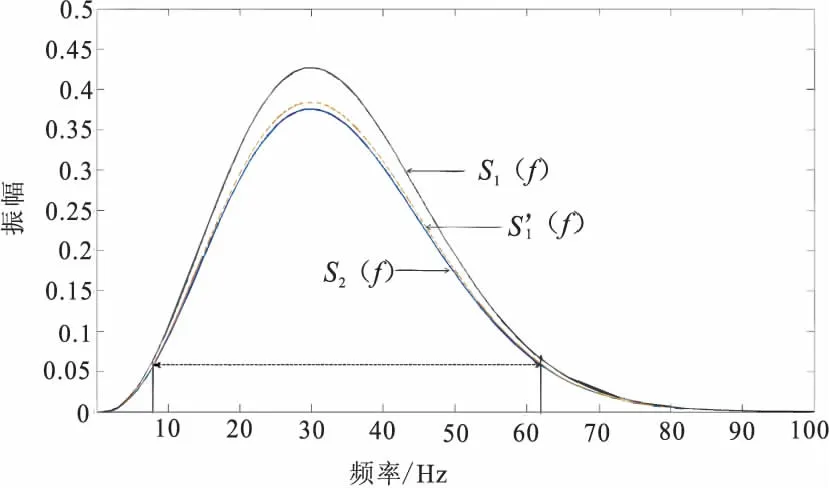
图1 地震波衰减前后振幅谱示意图Fig.1 Amplitude spectrumof the seismic wave attenuationbefore and after

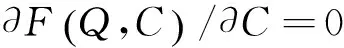
(5)

得到：

(6)

将C(Q)带入目标函数式(4)，得到新的目标函数为式(7)。

(7)

根据目标函数式(7)完成品质因子反演。

2 模型测试

设计5层各向同性水平层状介质模型，参考速度为2 000 m/s，各层厚度、品质因子Q参数见表1。采用30 Hz雷克子波生成VSP下行波记录，如图2所示。

根据图2所示模型数据，计算品质因子的值，并与谱比法估算结果对比如图3所示。图3(a)为基于振幅谱能量误差最小原则的品质因子提取方法提取结果，图3(b)为谱比法提取品质因子结果。从图3中可以看出，在无噪声干扰情况下，两种都能取得较好的效果，本文方法与谱比法的平均误差分别为0.34%、0.62%。在此基础上，加入一定的噪声干扰，进一步比较两种方法的提取结果，如图4、5所示。

表1 理论模型地层参数

Tab.1Formation parametersof theoretical model

D=200m Q=30D=100m Q=60D=100m Q=50D=100m Q=80D=100m Q=100

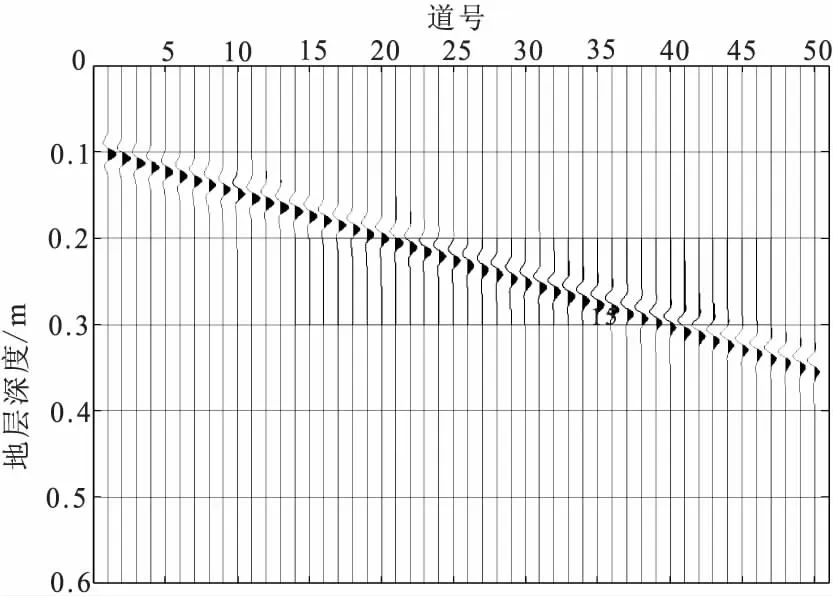
图2 无噪声VSP地震记录Fig.2 VSP seismogram without noise

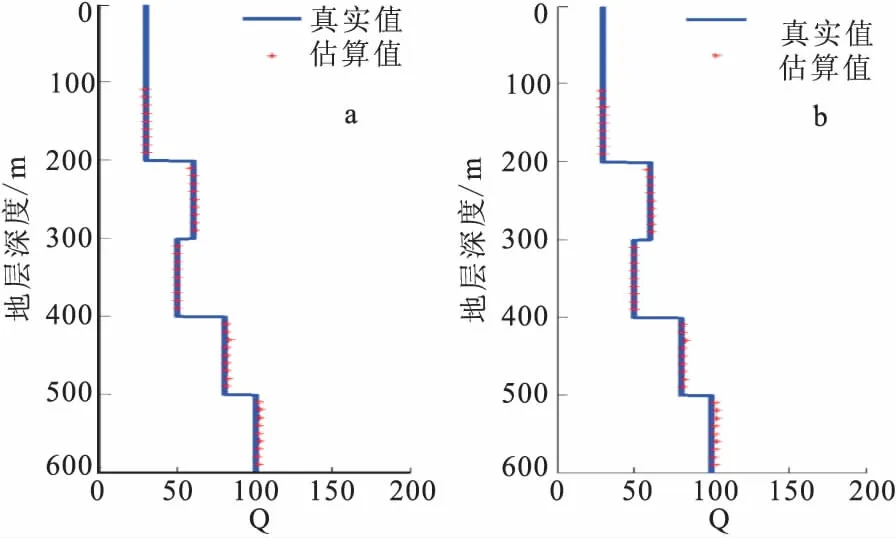
图3 本文方法与谱比法Q值估算结果Fig.3 The estimation results of this method and the spectral ratio method(a)本文方法;(b)谱比法

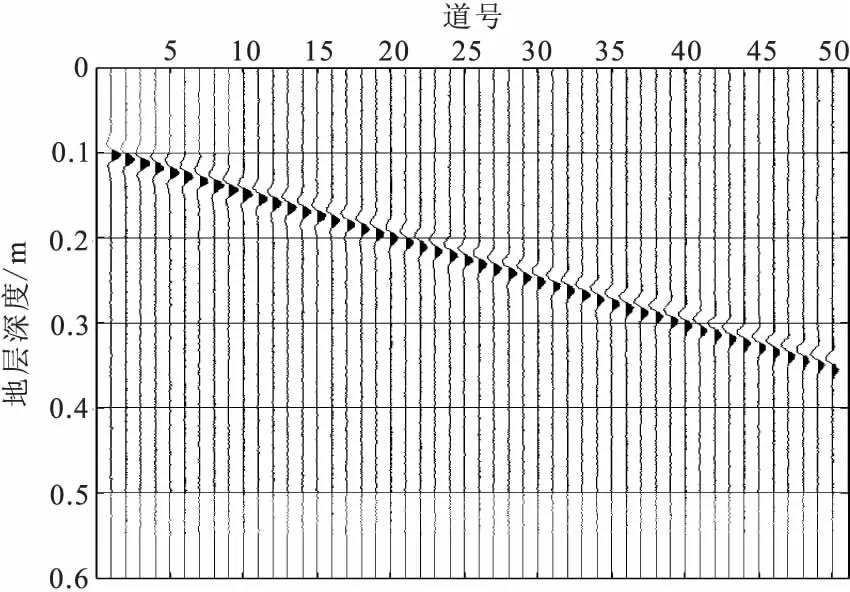
图4 图4含噪声VSP地震记录Fig.4 VSP seismogram with noise

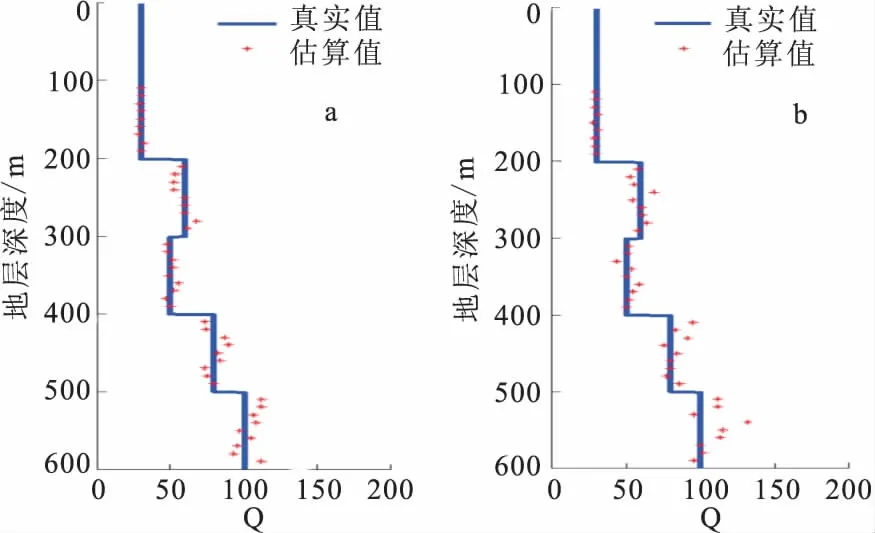
图5 本文方法与谱比法Q值估算结果 Fig.5 The estimation results of this method and the spectral ratio method(a)本文方法;(b)谱比法

在含噪条件下随着深度的增加，信噪比降低，两种方法的计算精度都会降低，并且估算值与真实值的误差逐渐增大。如图5所示，两种方法的估算误差分别为11.48%、18.23%。相比较而言，本方法估算结果更接近真实值。

为了进一步说明本方法估算结果的准确性，根据图2所示合成地震记录，在100 m～500 m深度之间以100 m为间隔取五道地震子波，并根据图3(a)所示估算结果开展反Q滤波补偿工作。如图6所示，通过反Q滤波结果可以看到不仅地震子波振幅得到补偿，而且相位畸变也得到准确的校正。

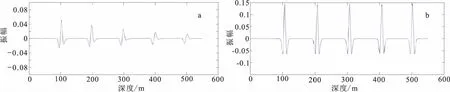
图6 补偿前后效果对比图Fig.6 The difference before and ofeer compensation(a)地震子波衰减示意图；(b)地震子波补偿示意图

综上所述，在无噪情况下本文方法估算得到的品质因子具有较好的准确性，可以对衰减子波得到较好的补偿。

3 实际资料处理中的应用

图7为某一工区实际零偏VSP下行波记录，共614道，道间距为3 m，时间采样间隔为1 ms。

利用该实际资料提取品质因子结果如图8、图9所示，图10为该工区测井速度曲线。对比品质因子的值与测井速度曲线的变化趋势，可以看到，品质因子与速度曲线具有较好的一致性。

从图8、图9、图10可以看出，实际资料提取结果与测井速度曲线随地层深度增加均呈增加的趋势。由椭圆区域明显可以看到，与谱比法相比本文方法反演得到的品质因子与测井速度曲线具有较好的一致性，并且在整个深度范围内Q值曲线变化更加平稳，比谱比法估算结果具有更好的稳定性。

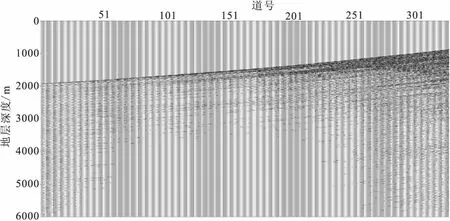
图7 零偏VSP下行波记录Fig.7 Zero-offset VSP seismogram

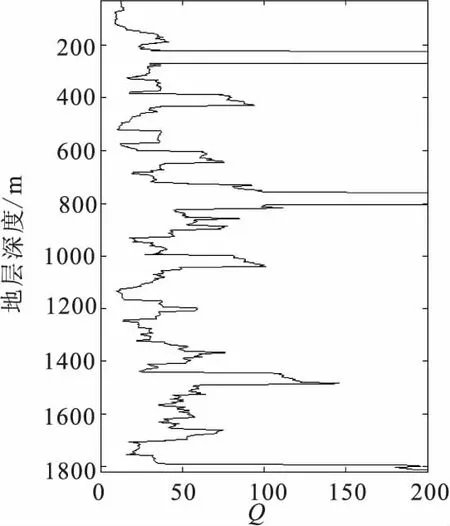
图8 实际资料提取结果(谱比法)Fig.8 Result of real data extraction

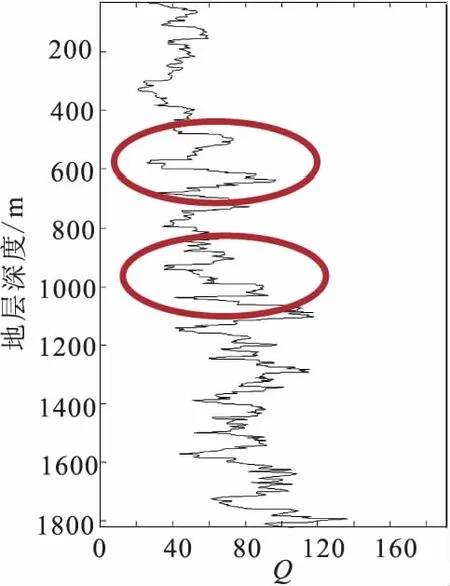
图9 实际资料提取结果(本文方法)Fig.9 Result of real data extraction

图10 测井速度曲线Fig.10 Logging speed curve

通过与测井速度曲线对比，表明基于振幅谱能量误差最小原则的品质因子提取方法，在实际资料处理中可以取得较好的效果。

4 结论

充分利用整个有效频带范围，根据地震波衰减前后振幅谱能量的差异，将Q作为反演参数，构建衰减前、后振幅谱能量误差随品质因子变化的目标函数，通过满足目标函数最小反演出地层最佳品质因子。相比常规的谱比法，本方法有效解决了频谱直接相除和频带拟合区间选取等引起不稳定性。

模型测试与实际资料处理表明，利用本方法提取品质因子可以取得较好的效果。但是本方法同样受噪声干扰显著，如何综合利用振幅谱与相位等信息提取高精度品质因子是需要进一步研究的方向。

[1]FUTTERMAN.Dispersive body waves[J].Journal of Geophysical Research,1962,7(13):5279-5291.

[2]ROBERT C.TYCE.Estimating acoustic attenuation from a quantitative seismic profiler[J].Geophysics,1981,46(10):1364-1378.

[3]D.JANNSEN,J.VOSS ,F.THEILEN.Comparison of methods to determine Q in shallow marine sediments fromvertical reflectionseismograms[J].Geophysical Prospecting,1985,33(4):479-497.

[4]GLADWIN M T,STACEY F D.Anelastic degradation of acoustic pulses in rock[J].Physics of the Earth and Planetary Interiors,1974,8(4):332-336.

[5]L.ENGELHARD.Determination of seismic-wave attenuation by complex trace analysis[J].Geophysical Journal International,1996,125(2):608-622.

[6]BATH M.Spectral Analysis in Geophysics[M].New York:Elsevier,1974.

[7]YOULI QUAN,JERRY M.HARRIS.Seismic attenuation tomography using the frequency shift method[J].Geophysics,1997,62(3):895-905.

[8]CHANGJUN ZHANG,TADEUSZ J.ULRYCHZ.Estimation of quality factors from CMP records[J].Geophysics,2002,67(5):1542-1547.

[9]LI H B,ZHAO W Z,CAO H，et al.Characteristicsof seismic attenuation of gas reservoirs in waveletdomainof Wavelet Scales[J].Chinese Journal of Geophysics,2004,47(5)：892-898.

[10]王小杰,印兴耀,吴国忱.基于叠前地震数据的地层Q值估计[J].石油地球物理勘探,2011,46(3):423-428.WANG X J,YIN X Y,WU G C.Estimation of stratigraphic quality factors on pre-stack seismic data[J].Oil Geophysical Prospecting,2011,46(3):423-428.(In Chinese)

[11]TONN R.The determination of the seismic quality factor Q from VSP data:A comparison of different computational methods[ J].Geophysical Prospecting,1991,39(1):1-27.

[12]宫同举,孙成禹,彭洪超,等.几种提取品质因子方法的对比分析[J].勘探地球物理进展，2009,32(4)：252-256.GONG T J,SUN C Y,PENG H C,et al.Comparative of several methods to extract quality factor[J].Progress in Exploration Geophysics,2009,32(4)：252-256.(In Chinese)

[13]YIH JENG,JING-YIH TSAI，SONG-HONG CHEN.An improved method of determining near-surface Q[J].Geophysics,1999,64(5):1608-1617.

[14]张大伟,孙赞东,王学军,等.利用零井源距VSP资料进行品质因子反演[J].石油地球物理勘探，2011,46(1)：47-52.ZHANG D W,SUN Z D,WANG X J ,et al.Q-factor inversion and calculation using zero-offset VSP data[J].Oil Geophysical prospecting,2011,46(1)：47-52.(In Chinese)

[15]E.BLIAS.Accurate interval Q-factor estimation from VSP data [J].Geophysics,2012,77(3):149-156.

[16]曹思远,谭佳,高明,等.对数谱根式法Q值反演[J].石油地球物理勘探，2014,49(1)：161-166.CAO S Y,TAN J,GAO M,et al.Seismic Q estimation with logarithmic spectrum equation root[J].Oil Geophysical prospecting,2014,49(1)：161-166.(In Chinese)

Study and application on the Q-factor extraction based on the principle of minimum energy error of amplitude spectrum

SUN Wen-guo,CAO Dan-ping*,FENG Ji-hao

(China University of Petroleum(east china) ,Qingdao 266580，China)

The quality factor Q is an important parameter to measure the energy of seismic wave attenuation,hydrocarbon reservoir identification and the compensation of seismic wave attenuation.Spectral ratio method is one of the most commonly used method in real data processing,but it is also effected by time window,band range selection and other human factors,so that the result of quality factor may be instability.This paper presents a method based on the principle of minimum energy error of amplitude spectrum to estimate Q,this method fully utilize the information of the entire frequency range of the amplitude spectrum,to estimate the quality factor by building objective function of amplitude spectrum energy with Q changes,effectively solve the effective by the spectrum direct division and the band selection and so on.Zero-offset VSP model tests show that the quality factor extraction method based on the principle of minimum energy error of amplitude spectrum has higher precision than the spectral ratio method,and obtained good results in the application of real data.

quality factor; VSP; energy of amplitude spectrum; index method; spectral ratio method

2015-09-15 改回日期：2015-10-09

国家重点基础研究发展计划“973计划”(2013CB228604)；山东省自然科学基金(ZR2014DM009)

孙文国(1990-)，男，硕士，主要从事地球物理探测方法与技术研究，E-mail：1274517937@qq.com。

*通信作者：曹丹平(1978-)，男，教授，主要从事地球物理理论、方法及应用研究，E-mail：caodp@upc.edu.cn。

1001-1749(2016)06-0810-05

P 631.4