基于决策树和逐步回归的大数据研究

［沈金榕 周杨景］

基于决策树和逐步回归的大数据研究

［沈金榕 周杨景］

针对大数据中自变量极多而导致的计算复杂，获取的自变量对因变量不显著等问题，提出了基于决策树的逐步回归解决方法。总结了其优点和局限性。

逐步回归 决策树 F检验 ID3算法

沈金榕

就职于中国电信广东研究院市场运营研究所，长期从事客户研究、移动互联网消费行为跟踪研究等方面工作。

周杨景

广东工业大学信息工程学院，硕士研究生，主要研究方向为数据库技术研究。中国电信广东研究院市场运营研究所专家，长期深耕客户研究、市场研究领域。

1 引言

我们生活在互联网时代，各行各业每时每刻都会产生大量的数据，这些数据表面上看都是毫无关联、杂乱无章的数据，但是数据的背后却隐藏着我们想不到的有用信息，面对着大量的数据，如何有效利用和处理这些数据，让数据为我们所用成为世界共同关系的问题。逐步回归法和决策树是目前在处理数据上用的比较多的方法。逐步回归法的基本思想是剔除对因变量不起作用或作用很小的因子，挑选出显著性因子，从而得到最优的回归模型。决策树的基本思想是利用树的结构对数据进行分类，采用自顶向下的方式，从树的根节点开始，对每一个叶节点进行属性值的测试比较，然后按照给定实例的属性值确定对应的分枝，最后在决策树的叶子节点得到结论。其中这个过程在以新的节点为根的子树上重复[2]。

在回归分析中，自变量之间的多重相关性是遇到的最典型的问题，变量之间的多重相关性会严重损害参数估计的准确性和合理性，扩大模型误差，并破坏模型的稳健性。逐步回归法能够克服自变量的多重共线性，免去多重共线的复杂计算，而决策树方法有良好的预测准确性，能够快速分类，可以作为一种衡量变量价值大小，寻找最佳变量的工具。但是存在一个问题，当自变量较多时，并不是所有的自变量都会对因变量产生显著影响，如果只使用逐步回归方法剔除自变量，计算量非常大，耗费的时间较多，由于决策树具有快速准确的寻找最佳变量，准确性高，计算复杂度低，在众多自变量中，先采用决策树方法选择出重要的自变量集合，然后使用逐步回归方法建立自变量与因变量的关系，得到回归方程。

2 逐步回归方法

逐步回归方法中全部自变量按其对因变量的贡献程度大小，由大到小逐个引入回归方程，对那些因变量作用不显著的自变量不会被引入回归方程中，已被引入回归方程的自变量在引入新自变量进行F检验后失去重要性时，需要从回归方程中剔除。逐步回归的基本步骤可用图1描述。

图1 逐步回归的基本步骤

下面简明给出逐步回归法的求解。

设有m个自变量，n组观察值，得到m元的线性回归模型为

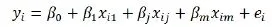
其中，i=1,2,…,n表示第i组观察值，j=1,2,…,m表示第j个自变量，表示偏回归系数，表示随机误差。

（1）进一步计算未选入自变量的偏决定系数：

其中i是还没被选入的一个自变量。

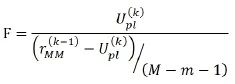
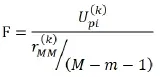
上述步骤循环重复，直到所有对因变量有显著作用的自变量都已选入，对因变量没有显著作用的自变量都已剔除，从而获得回归方程。

3 决策树方法

决策树是一个可以自动对数据进行分类的树形结构，是树形结构的知识表示，可以直接转换为决策规则。

决策树生长过程可用图2描述：

下面是决策树的构建过程[8]：

输入：节点n，数据集D，分割方法(Splitting Selection Method)CL

输出：以节点n为根节点的基于数据集D、分割算法CL的决策树

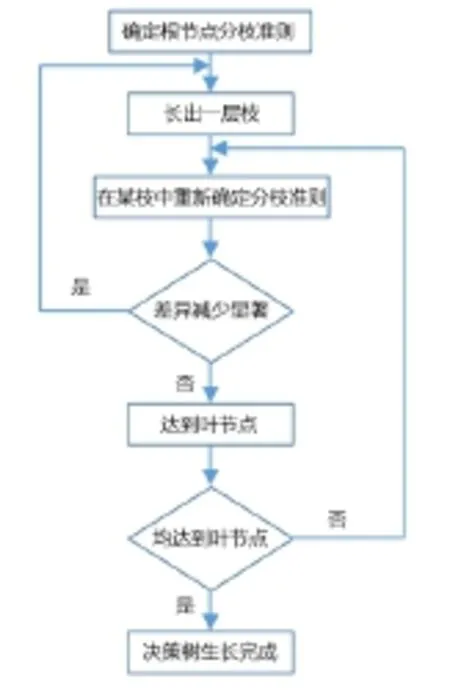
图2 决策树生长过程

Procedure BuildTree

初始化树的根节点；

在D中计算CL来求解节点n的分割标准(Splitting Cirterion)；

if(节点n满足分割条件)

4 基于决策树的逐步回归法

决策树包含很多生成算法，经典的ID3算法，它具有高效、准确等特点。ID3算法是以信息熵的下降速度作为测试属性的标准，就是选择使得信息增益度公式中值最大的属性作为测试属性。该算法根据属性集的取值选择实例的类别，核心是在决策树上各级节点上选择属性，用信息增益率来作为属性选择标准，使得在每一非叶节点进行测试时，系统的熵值最小，期望该非叶节点到达各后代叶节点的平均路径最短，生成的决策树平均深度较小，从而获取对因变量具有显著重要的自变量，再把这些自变量采用逐步回归法建立和因变量最有显著影响的自变量和因变量的回归方程。

5 结语

逐步回归克服多重共线性，决策树预测准确度高，寻找最佳变量等优点，使得它们在这个大数据时代应用的非常广，在自变量很多的时候，为了避免逐步回归计算复杂，采用决策树的ID3算法对自变量进行筛选，找出对因变量影响大的自变量，在通过逐步回归方法建立自变量与因变量的回归方程。逐步回归方法也有局限性，如果某一变量只对因变量影响显著而对其余变量作用不显著时，那么对该自变量作显著性检验，很可能该自变量不能引入方程，最终得到的回归方程不是最优的。决策树存在过度拟合问题，不能解决增量数据集等问题。这些都是今后值得深入研究的问题。

1 王冬梅,沈颂东.逐步回归分析法[J].工业技术经济,1997,03:54-57

2 冯少荣.决策树算法的研究与改进[J].厦门大学学报(自然科学版),2007,04:496-500

3 JohnDurkin,蔡竞峰,蔡自兴.决策树技术及其当前研究方向[J].控制工程,2005,01:15-18+21

4 S. Sonoda, Y. Takahashi, K. Kawagishi, N. Nishida and S. Wakao, "Application of Stepwise Multiple Regression to Design Optimization of Electric Machine," in IEEE Transactions on Magnetics, vol. 43, no. 4, pp. 1609-1612, April 2007

5 Y. Lan and S. Guo, "Multiple Stepwise Regression Analysis on Knowledge Evaluation," Management of e-Commerce and e-Government, 2008. ICMECG '08. International Conference on, Jiangxi, 2008, pp. 297-302

6 N. Zhou, Z. Huang, F. Tuffner, D. Trudnowski and W. Mittelstadt, "A modifed stepwise linear regression method for estimating modal sensitivity," 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, 2011, pp. 1-7

7 周元娇.筛选逐步回归方法的改进研究[D].扬州大学,2011

8 王威.基于决策树的数据挖掘算法优化研究[D].西南交通大学,2005

9 Mircea Eremia; Chen-Ching Liu; Abdel-Aty Edris, "Decision Trees," in Advanced Solutions in Power Systems:HVDC, FACTS, and Artifcial Intelligence , 1, Wiley-IEEE Press, 2016

10 Dydo, J. G. Bazan, S. Buregwa-Czuma, W. Rząsa and A.

Skowron, "Verifying cuts as a tool for improving a classifer based on a decision tree," 2016 Federated Conference on Computer Science and Information Systems (FedCSIS), Gdansk, Poland, 2016

11 Swetapadma; A. Yadav, "A Novel Decision Tree Regression Based Fault Distance Estimation Scheme for Transmission Lines," in IEEE Transactions on Power Delivery , vol.PP, no.99, pp.1-1

12 邵俊.基于逐步回归预测模型的话务管理系统设计[D].复旦大学,2013

13 杨学兵,张俊.决策树算法及其核心技术[J].计算机技术与发展,2007,01:43-45

2016-11-24）

10.3969/j.issn.1006-6403.2016.12.011