中等间距比条件下串列双圆柱流致振动数值模拟

韩 冰，及春宁，刘 爽，陈威霖

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中交第一航务工程勘察设计院有限公司，天津 300222）

中等间距比条件下串列双圆柱流致振动数值模拟

韩 冰1，及春宁1，刘 爽2，陈威霖1

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中交第一航务工程勘察设计院有限公司，天津 300222）

在上下游圆柱最大振幅较单圆柱的都有较大提升，下游圆柱所受的阻力均值小于上游圆柱的阻力均值，而下游圆柱的升力均方根值在折合流速较小时（Ur＜6.1）比上游圆柱的小，在折合流速较大时（Ur＞6.1）比上游圆柱的大。发现了两种尾流模式，分别为单阻流体模式（SG模式）和剪切层重附着模式（AG模式）。

串列双圆柱；流致振动；响应分支；尾流模式；浸入边界法

引 言

由于海流的流量和流向都比较稳定，其完全可以成为人类可靠的能源之一。在这一领域，美国密歇根大学的Bernitsas教授及其（团队利用海流流经圆柱群所激发的圆柱涡激振动，开发了一种低速海流能利用装置[1]，称为 VIVACE（Vortex-Induced Vibration Aquatic Clean Energy）。该装置具有造价低、不易损坏、可规模化发电、不影响通航等优点。然而，圆柱群涡激振动是一个复杂的流固耦合过程，目前对其振动机理尚未完全掌握。本文旨在针对VIVACE的简单形式——串列双圆柱在均匀流场中的流致振动进行数值模拟，精细化地研究其振动响应和尾流模式随折合流速的变化过程。

1 研究现状

目前为止，研究者对圆柱的涡激振动从物理实验和数值模拟两个方面进行了大量的研究。Khalark和 Williamson[2]实验研究了弹性支撑的低质量比、低阻尼比圆柱的涡激振动。他们认为：质量比（m*=m/mf，m为圆柱的质量，mf为圆柱排开流体的质量）决定了圆柱振动响应随折合流速Ur（Ur=U/fnD ，U为来流速度， fn为结构在水中的自然频率，D为圆柱直径）的变化过程，而质量比m*和阻尼比ζ的组合参数（m*ζ）决定了最大响应振幅的大小。进一步地，Khalark和Williamson[3]在小m*ζ参数实验中发现了三支响应，分别为：初始分支（initial branch）、上端分支（upper branch）和下端分支（lower branch）。最大响应振幅发生在上端分支。

与单圆柱涡激振动相比，串列双圆柱流致振动对尾流的影响更大[4～5]。当圆柱间距比s/D（s为两圆柱中心之间的距离）较小时，下游圆柱的存在会显著改变上游圆柱的尾流形态，上游圆柱对下游圆柱的影响则会一直延续到很大的间距比[6]。Zdravkovich[7]根据串列圆柱的柱间流态的不同，将尾流模式划分为 3个不同的模式：延展体模式（1.0＜s/D＜1.2～1.8）、剪切层重附着模式（1.2～1.8＜s/D＜ 3.4～3.8）和共同脱涡模式（s/D＞ 3.4～3.8）。剪切层重附着模式是延展体模式和共同脱涡模式的过渡模式，其中涉及许多复杂的流固耦合过程，如剪切层的分离和重复着、上游圆柱剪切层与下游圆柱泄涡之间的涡旋动力过程、复杂的间隙流动、下游圆柱的负阻力和高频升力现象等，是串列双圆柱涡激振动研究中最复杂的部分。本文所做研究刚好处于剪切层重附着区域。

Prasanth和Mittal[8]对雷诺数Re=100串列双圆柱两自由度流致振动进行了数值模拟研究，发现：下游圆柱在横向和流向上都有很大的振幅，横向振幅最大值达到了1.1D，几乎是该雷诺数下单圆柱涡激振动振幅的2倍。Bokaian和Geoola[9]实验研究发现：上游圆柱受下游圆柱的影响仅在间距比s/D＜2.0时显著。Borazjani和Sotiropoulos[10]对雷诺数Re=200、间距比s/D=1.5下串列双圆柱流致振动的数值模拟发现：当间隙流活跃时，尾流过渡到弱三维状态，但此时三维效应太弱，不会影响系统的动力响应，因此三维计算结果和二维计算结果是相同的。Mizushima和Suehiro[11]研究发现：当间距比s/D＜4.0时，临近圆柱的存在会对周围流动起到稳定作用。

总之，串列圆柱的涡激振动机理要比单圆柱复杂很多。当间距比较小（/2s D=）时，上下游圆柱的振动会互相影响彼此，并与周围流体发生复杂流固耦合过程。

2 数值方法和计算参数

本文采用浸入边界法进行流固耦合的数值模拟。浸入边界法的基本思想是在Navier-Stokes方程中增加附加体积力项来表示流体和固体之间的相互作用，其主要特点为：整个流场使用简单的笛卡尔网格进行计算，处理动边界时无需重建网格，通过移动浸入边界点来模拟物面运动。有关浸入边界法的详细介绍参见文献[12～16]。

本文针对中等间距比（s/D=2）条件下的串列圆柱流致振动开展数值模拟研究，圆柱的质量比为m*=2，雷诺数为 Re=100，折合流速在Ur=2.0～16.0之间变化。折合流速的步长较小，最小为ΔUr=0.1，以期对串列双圆柱之间复杂的相互作用进行精细化研究。模拟中，计算域的大小为：计算域宽度H=100D，长度Lx=200D，两圆柱的中点距离来流边界Lu=100D，距离出流边界Ld=100D。以两圆柱圆心连线的中点为原点，圆柱的初始位置坐标分别为(1.0,0.0)和(-1.0,0.0)，如图1所示。网格采用非均匀正交矩形网格，在圆柱的周围设置加密区，大小为8D×4D。加密区内，网格为均匀网格，网格边长为Δx=Δy=D /64。无量纲时间步长为ΔtU/D =0.005，以满足数值算法对CFL条件的要求，即：CFL=UΔ t/Δx ＜0.5。

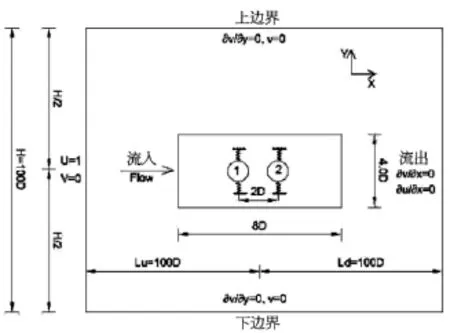
图1 串列双圆柱流致振动的计算域和边界条件示意

3 串列双圆柱流致振动响应和尾流模式

3.1 串列双圆柱的振幅随折合流速的变化

如图2所示，折合流速Ur≤3.1时，上下游圆柱振幅均非常小，接近于零。当折合流速Ur≥3.2以后，两圆柱响应幅值均迅速增加。到Ur=4.5时，上游圆柱的振幅趋于稳定，形成一个较为平整的台阶（ Ymax/D≈0.68），直到Ur=7.2时结束。之后，上游圆柱最大振幅随着折合流速的增加开始不断下降，并逐渐趋于稳定。与上游圆柱相比，下游圆柱自折合流速Ur≥3.2后，响应幅值均迅速增加，到折合流速Ur=3.5时出现拐点，增长速率略微减缓，到Ur=4.0时出现第二个拐点，增长速率再次突增，并在Ur=6.3时最大振幅与上游圆柱持平。随后继续增长，且增长速率不断增大，到Ur=7.5时下游圆柱振幅达到峰值 Ymax/D=1.0623。之后开始缓慢下降，但振幅始终高于上游圆柱。

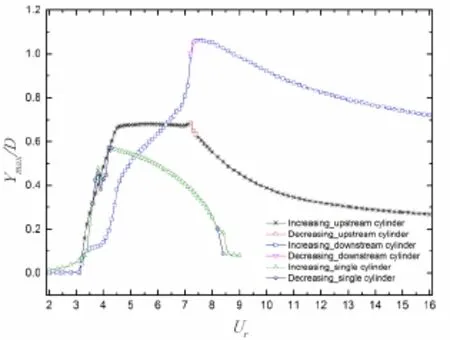
图2 圆柱最大振幅随折合流速的变化

参考单圆柱涡激振动的振动响应分支分类方法，串列双圆柱流致振动中，上游圆柱的流致振动响应可分为三个阶段，分别为初始分支、稳定分支和下端分支；下游圆柱的振动响应也可以分为三个分支，分别为初始分支、过渡分支和下端分支。两个圆柱的分支分别一一对应，起止的折合流速范围分别为3.4≤Ur≤4.2（第一分支）、4.7≤Ur≤7.2（第二分支）和Ur≥7.2（第三分支）。在第一分支之前，两个圆柱基本不发生振动。在第一分支内，上下游圆柱的振幅均快速增大，但上游圆柱的振幅总是大于下游圆柱的振幅。在第二分支内，上游圆柱的振幅达到平台阶段，基本保持不变，最大值在此分支内取得，下游圆柱的振幅依旧继续增大，并在此分支内超越上游圆柱的振幅。在第三分支内，上下游圆柱的振幅单调递减，并有趋于稳定的趋势，上游圆柱的振幅始终小于下游圆柱的振幅，下游圆柱的振幅最大值在该分支的起始处取得。

间距比s/D=2.0时，串列双圆柱的上游圆柱由于受到下游圆柱振动的影响，其流致振动响应明显区别于单圆柱的涡激振动响应。对比单圆柱涡激振动的响应，可发现：1）上游圆柱的响应虽然呈现出初始分支和下端分支，但上游圆柱的响应幅值要大于单圆柱涡激振动，上游圆柱的最大振幅Ymax/D=0.686比单圆柱涡激振动的最大振幅Ymax/D=0.573大了19.7 %；2）在下端分支中，上游圆柱的振幅远大于单圆柱涡激振动的情况，即使随着折合流速增加而缓慢下降，直到Ur=16.0时上游圆柱依旧维持在较大振幅上，始终未出现单圆柱涡激振动中的非同步区域；3）上游圆柱始终未出现迟滞现象，且没有发生任何振幅跳跃现象，而单圆柱涡激振动响应在初始分支中和下端分支结束时分别出现和迟滞和跳跃现象。

3.2 串列双圆柱所受升阻力随折合流速的变化

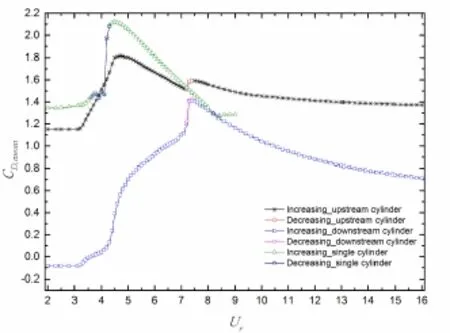
图3 圆柱所受阻力均值折合流速的变化

如图3所示，上游和下游圆柱的阻力均值明显不同，上游圆柱的阻力均值始终大于下游圆柱的阻力均值。当折合流速Ur≤3.2时，下游圆柱受到的阻力均值为负值，此时上游圆柱分离的剪切层将两圆柱包裹在一起，并从下游圆柱后卷起，形成旋涡脱落。此阶段内，下游圆柱始终处于上游圆柱的尾流当中，由于上游圆柱的遮蔽效应，下游圆柱的阻力均值小于零。当折合流速Ur＞3.4以后，两圆柱的响应振幅已经显著地增加，下游圆柱已经可以部分地移出上游圆柱的尾流，其阻力均值也变为正值。上游圆柱的阻力均值在平稳分支的开端（Ur=4.7）达到峰值CD,mean=1.816。随后上游圆柱阻力均值开始下降，直到平稳分支的结束（Ur=7.2）出现一个小幅跳跃。下游圆柱的阻力均值在下端分支的开端（Ur=7.2）达到峰值CD,mean=1.421。最后，当折合流速Ur＞7.5之后，上下游圆柱阻力均值开始不断缓慢下降，上游圆柱的阻力均值最终趋于固定圆柱绕流中圆柱受到的阻力均值。

图4 圆柱所受升力均方根值随折合流速的变化

如图4所示，在折合流速Ur≤3.2时，上下游圆柱的升力均方根值几乎为零。在初始分支中，上游圆柱的升力均方根值急剧上升，在初始分支的末端（Ur=4.3）达到最大值CL,rms=1.366。随后，在平稳分支中，上游圆柱的升力均方根值迅速减小，并在平稳分支的末端出现小幅跳跃。在下端分支中，上游圆柱的升力均方根值缓慢增大，并最终趋于稳定。与上游圆柱升力均方根值的变化趋势不同，下游圆柱的升力均方根值在初始分支和过渡分支中均呈现出缓慢下降的趋势，仅在初始分支的开端和初始分支的结束发生大幅的跳跃式增长。在过渡分支的开端（Ur=4.6)，下游圆柱升力均方根值达到峰值CL,rms=0.728。在下端分支中，下游圆柱的升力均方根值缓慢增大，并最终趋于稳定。对比上下游圆柱的升力均方根值发现，小折合流速时，上游圆柱的升力均方根值大于下游圆柱的，大折合流速时，上游圆柱的升力均方根值小于下游圆柱的。两者升力均方根值大小关系的交替发生在第二分支中部，即Ur=6.1处。此时，恰好对应上下游圆柱振幅的大小关系发生交替（见图2所示）。

3.3 串列双圆柱流致振动频率随折合流速的变化

当折合流速Ur≤3.1时上下游圆柱升力的卓越频率（反映了振动响应的频率）稳定在St=0.122左右，而此时圆柱的振动响应和升力均方根值均在零附近。如图5所示，当Ur=3.1时，升力的卓越频率跳跃至St=0.216。之后，随折合流速增大而不断下降。直到折合流速Ur=7.4才又发生一个大幅跳跃。其原因为：在第二和第三分支切换的时候，由于圆柱间复杂的相互作用，上下游圆柱的升力卓越频率由一倍基频跳跃到三倍基频上，直到折合流速Ur=8.6时，再次跳回到一倍基频。在此阶段，两个圆柱的升力卓越频率不稳定，间或地跳回一倍基频。圆柱升力卓越频率的这种跳跃现象与圆柱间不稳定的相互作用相关。到折合流速Ur=8.6之后，上下游圆柱的升力卓越频率稳定在一倍基频上，并缓慢下降。在整个过程中，上下游圆柱升力卓越频率离圆柱振动系统的固有频率均较远，这与本文所采用圆柱的质量比较低有关。圆柱的质量比越低，振动时的附加质量对振动体系固有频率的影响越显著。

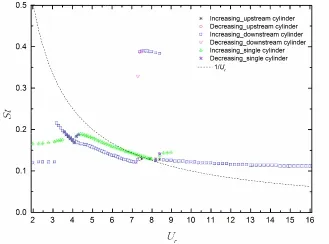
图5 圆柱所受升力的卓越频率随折合流速变化

3.4 串列双圆柱流致振动尾流模式

Sumner[17]对串列双圆柱绕流研究成果进行了系统的归纳，发现存在三种不同的尾流模式，分别为单阻流体模式（single bluff-body regime）（Zhou和Yiu[18]称之为延展体模式（extended body regime））、剪切层重附着模式（reattachment regime）、共同脱涡模式(co-shedding regime)。Carmo等[19]将低雷诺数串列双圆柱绕流的尾流模式分为SG模式（symmetric in the gap）、AG模式（alternating in the gap）和WG模式（wake in the gap）三种。当圆柱自由振动时，圆柱和流体之间的相互作用会更加强烈，尾流模式也会更加复杂。

对间距比为s/D=2、折合流速Ur=2.0～16.0下的串列双圆柱尾流模式总结如下：

1）当折合流速2.0≤Ur≤3.1时，两圆柱的振动响应均较小，从上游圆柱分离剪切层将两圆柱包裹在一起，并从下游圆柱后方脱落，形成交替脱落的单涡街，此时两圆柱的间隙没有旋涡，对应下游圆柱的阻力均值为负，如图6（a）所示。此时的尾流模式属于单阻流体模式或者SG模式。

2）当折合流速3.2＜Ur≤4.6时，两圆柱的振幅急剧增加，下游圆柱部分移出上游圆柱的尾流区，此时上下游圆柱之间开始有流体掺混。上游圆柱开始脱落漩涡，并撞击到下游圆柱使其迎流侧出现涡量，下游圆柱阻力均值变为正值。此时，下游圆柱后出现一列窄涡街，如图6（b）所示。此时的尾流模式属于剪切层重附着模式或者AG模式。

3）当折合流速4.7＜Ur≤7.2时，上游圆柱振幅虽然稳定不变，但下游圆柱振幅仍在不断增大。上游圆柱脱落的漩涡完全从两圆柱间隙通过，此时上游圆柱脱落的漩涡对下游圆柱起到了最大的促进作用，此阶段下游圆柱振幅处在较高水平上。脱落的漩涡形成一列宽涡街，一直维持到较远的下游才发生融合，如图6（c）所示。此时的尾流模式属于剪切层重附着模式或者AG模式。

4）当折合流速7.4＜Ur≤16.0时，上下游圆柱振幅开始下降，从上游圆柱脱落的旋涡不能完全从两圆柱的间隙通过，上游圆柱脱落旋涡的一部分附着于下游圆柱的迎流侧，因此使得下游圆柱的阻力有所下降。随着折合流速的增加，旋涡之间的间距逐渐增加，逐步形成稳定的一列窄涡街，如图6（d）所示。此时的尾流模式属于剪切层重附着模式或者AG模式。

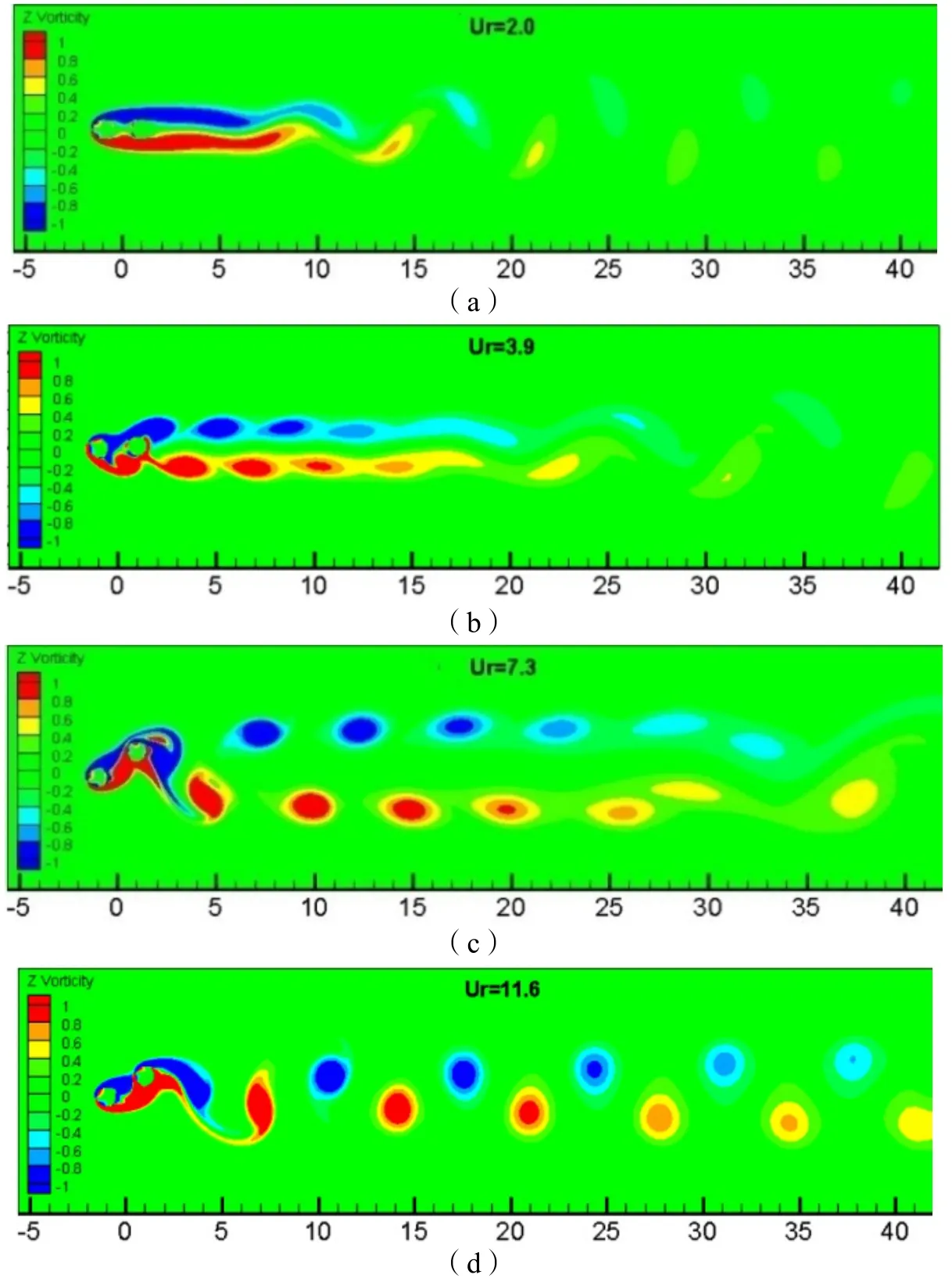
图6 不同折合流速下串列双圆柱流致振动的尾涡模式

4 结 论

通过对间距比s/D=2.0的串列双圆柱流致振动进行精细化数值模拟，总结了串列双圆柱的振动响应、流体力特性以及尾涡模式随折合流速的变化过程，研究了两圆柱之间的耦合作用，为理解串列双圆柱流致振动机理提供了详实的数据。本文主要结论归纳如下：

1）两个圆柱的振动响应曲线均出现了三个响应分支。对上游圆柱，分别为：初始分支、稳定分支和下端分支；对下游圆柱，分别为：初始分支、过渡分支和下端分支。两个圆柱的分支相互对应。当折合流速较小时（Ur＜6.1），上游圆柱的振幅大于下游圆柱的振幅，当折合流速较大时（Ur＞6.1），上游圆柱的振幅小于下游圆柱的振幅。

2）与单圆柱涡激振动响应相比，上下游圆柱最大振幅大幅提升，上游圆柱的最大振幅达到Ymax/D=0.686，而下游圆柱的最大振幅达到Ymax/D=1.062，分别比单圆柱涡激振动的最大振幅增大了19.7 %和85.3 %。串列双圆柱的锁定区间也比单圆柱的大很多，直到本文的最大折合流速Ur=16.0时，上下游圆柱依旧没有脱离锁定区间，处于大振幅振动状态。

3）下游圆柱阻力均值在小折合流速下出现负值，随着圆柱振幅的增大，下游圆柱的阻力均值变为正值。下游圆柱所受的阻力均值均小于上游圆柱的阻力均值，而下游圆柱的升力均方根值在折合流速较小时（Ur＜6.1）比上游圆柱的小，在折合流速较大时（Ur＞6.1）比上游圆柱的大。

4）圆柱升力的卓越频率大体上呈现出随折合流速的增大而减小的趋势，在Ur=3.1、Ur=7.4和Ur=8.6出现了不连续的跳跃。在7.4＜Ur＜8.6之间，升力的卓越频率由一倍基频跳跃至三倍基频，其原因与圆柱间的不稳定的相互作用有关。

5）由于圆柱之间的距离较小，本文共发现了两种尾流模式，分别为单阻流体模式（SG模式）和剪切层重附着模式（AG模式）。

[1]Bernitsas M M,Raghavan K.Fluid Motion Energy Converter[M].International Provisional Patent Application,U S Patent and Trademark Office,2005.

[2]Khalak A,Williamson C H K.Dynamics of a hydroelastic cylinder with very low mass and damping[J].Journal and Fluids and Structures,1996,10:455-472.

[3]Khalark A,Williamson C H K.Fluid forces and dynamics of a hydroelastic structure with very low mass and damping[J].Journal and Fluids and Structures,1997,11:973-982.

[4]Chen S.A review of flow-induced vibration of two circular cylinders in crossflow[J].Journal of Pressure Vessel Technology,1986,108:382-393.

[5]Assi G R S,Meneghini J R,Aranha J A P,et al.Experimental investigation of flow-induced vibration interference between two circular cylinders[J].Journal of Fluids and Structures,2006,22:819-827.

[6]Papaioannoua G V,Yuea D K P,Triantafylloua M S,et al.On the effect of spacing on the vortex-induced vibrations of two tandem cylinders[J].Journal of Fluids and Structures,2008,24:833-854.

[7]Zravkovich M M.The effects of flow interference between two circular cylinders in various arrangements [J].Journal of Fluids and Structures,1987,1:239-261.

[8]Prasanth T K,Mittal S.Flow-induced oscillation of two circular cylinders in tandem arrangement at low Re[J].Journal of Fluids and Structures,2009,25:1029-1048.

[9]Bokaian A,Geoola F.Proximity-induced galloping of two interfering circular cylinders[J].Journal of Fluid Mechanics,1984,146:417-449.

[10]Borazjani I,Sotiropoulos F.Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region[J].Journal of Fluid Mechanics,2009,621:321-364.

[11]Mizushima J,Suehiro N.Instability and transition of flow past two tandem circular cylinders[J].Physics of Fluids 17,2005:104-107.

[12]Chen W,Ji C,Wang R,et al.Flow-induced vibrations of two side-by-side circular cylinders:Asymmetric vibration,symmetry hysteresis and near-wake patterns [J].Ocean Engineering,2015,110,244-257.

[13]Chen W,Ji C,Xu W,et al.Response and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar cross-flow[J].Journal of Fluids and Structures,2015,55:218-236.

[14]Ji C,Munjiza A,Williams J J R.A novel iterative direct-forcing immersed boundary method and its finite volume applications[J].Journal of Computational Physics,2012,231(4):1797-1821.

[15]Ji C,Xiao Z,Wang Y,et al.Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder at low Reynolds number using the fictitious domain method[J].International Journal of Computational Fluid Dynamics,2011,25(4):207-221.

[16]及春宁,杨立红,黄继露,等.串列双圆柱流致振动数值模拟[J].港工技术,2014,51(3):1-6.

[17]Sumner D.Two circular cylinders in cross-flow:A review[J].Journal of Fluids and Structures,2010,26:849-899.

[18]Zhou Y,Yiu M W.Flow structure,momentum and heat transport in a two-tandem-cylinder wake[J].Journal of Fluid Mechanics,2006,548:17-48.

[19]Carmo B S,Meneghini J R,Sherwin S J.Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing [J].Physics of Fluids,2010,22:54-101.

Numerical Simulation of Flow-induced Vibration of Two-cylinder in Tandem with a Medium Spacing Ratio

Han Bing1,Ji Chunning1,Liu Shuang2,Chen Weilin1
(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China; 2.CCCC First Harbor Consultants Co.,Ltd.,Tianjin 300222,China)

s:The maximum vibration amplitudes of cylinders at upstream and downstream are raised to a larger extent in comparison with single cylinder.The mean resistance against the downstream cylinder is smaller than that of the upstream cylinder,while the root-mean-square (r.m.s) of lift force against the downstream cylinder is smaller than that of the upstream cylinder in case of Ur＜6.1 but larger in case of Ur＞6.1.In addition,two wake-stream patterns are summarized,i.e.single resistance fluid pattern (SG) and shear-layer attached pattern (AG).

two-cylinder in tandem; flow-induced vibration; response branch; wake-stream pattern; immersed boundary method

P751；TB532

：A

：1004-9592（2016）06-0001-06

10.16403/j.cnki.ggjs20160601

2015-12-08

国家自然科学基金资助项目（51579175，51209161，51479135）

韩冰（1990-），男，助理工程师，主要从事施工组织和概预算工作。