直觉、优化、升华——由“点到直线距离公式的推导”引发的思考

☉江苏省江阴市华西实验学校 陈 艳

直觉、优化、升华
——由“点到直线距离公式的推导”引发的思考

☉江苏省江阴市华西实验学校 陈 艳

众所周知，“点到直线的距离”这节课的重心是引导学生自主推导点到直线的距离公式.教材（人教A版）试图通过“构造法”（构造直角三角形）让学生经历直线的距离公式的思维过程，深刻领会蕴含于其中的数学思想和方法，特别是在坐标法使用过程中渗透数形结合、化归等数学思想.但实际教学中，教材提供的解决方案学生很难自然想到，这就很容易产生两种教学“误区”，一种是教师把教材奉为经典强行灌输给学生，从而导致教学与学生认知水平脱节；另一种是回避教材的方案，采用自认为的“简便方法”、“巧妙方法”，推导方法五花八门，让人应接不暇.实际上，方法抉择不仅要考虑方法的本身，还应考虑把新旧知识的联系、学生的知识储备、学生的接受能力等多方面的因素.只有这样，公式推导过程方能自然和谐，才能被学生真正理解和掌握.

一、直觉：开启最自然的学习过程

学生在尝试解决复杂数学问题时，一般预先要考虑到几种可能的思路，究竟先选择哪个思路？放弃或暂时搁置哪个思路？单凭逻辑思维往往是解决不了的，这就需要运用直觉思维.所谓的数学直觉思维是以—定的知识经验为基础，通过对数学对象作总体观察，在一瞬间顿悟到对象的某方面的本质，从而迅速做出估计判断的一种思维.直觉思维可以帮助学生分析数学现象、猜想数学命题、顿悟解题思路、缩短思维过程、培育数学灵感等.因此，教师在教学中应立足于学生的直觉思维.

数学直觉体现在“点到直线距离公式的推导”就是“在没有外部条件的干预下，学生会怎么思考这个问题？会首先采用什么方法？”最自然、最朴素的方法莫过于“求出垂足坐标，利用两点间的距离公式直接推导”，但遗憾的是教材中的一句话“上述方法虽然思路十分自然，但具体运算需要一定的技巧”严重地打击了学生继续探究的勇气，也为教师避开这一方法提供了借口，但事实真的如此吗？

方法一：如图1所示，已知点P（x0，y0），直线l：Ax+By+C=0（A2+ B2≠0），PQ⊥l，垂足为Q.

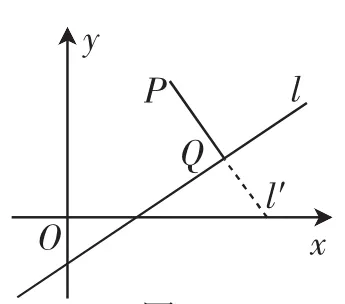
图1

设直线PQ的方程为y-y0=（x-x）（A≠0），即Bx-Ay=Bx0- Ay0，设点Q（x1，y1）.

虽然上述运算过程相对烦琐，但并没有涉及比较深奥的运算技巧.实际上，学生的数学学习是不断地尝试、摸爬，积累经验的过程.倘若跳过这一过程，直接抛给学生一个“简单、快捷”的思路，那么这对学生数学思维的训练来说的确是一个“遗憾”.

二、优化：在反思与改进中生成

虽然说数学直觉是对数学问题及其本质属性的直接感悟，但它受限于学习者已有的认知水平；虽然它是学习者数学思维最“自然”的流露，但它所呈现出来的结果并非是最理想的状态，有时甚至与教学预期背道而驰.因此，后续教学的重点应该是在学生直觉思维的基础上，把已有的知识经验加以改组，进而实现学生数学思维的优化.

方法一虽然自然，但此方法无法全面展示解析几何思想方法的精髓，比如：数形结合、整体代换、设而不求等.因此，很有必要采用多种方法对“点到直线的距离公式”进行探究，从而让学生在公式推导的过程中逐步体会解析几何的基本思想方法.当然，这些方法应建在原有方法基础上的改进与优化，而不能是毫无章法的“狂轰滥炸”.

思考：导致“方法一”烦琐的原因是什么？

分析：垂足Q的坐标表示比较复杂，从而导致运算烦琐.如果能够避开求垂足Q的坐标，那么运算就会变的简单.对于两点间距离公式如果不直接求x1，y1，消元与换元也是常用的运算手段.于是，我们不妨思考如何把x1，y1两个参数变成一个参数或者所学的知识中，哪个量或者式子包含了“（x1-x0）、（y1-y0）”？

方法二：利用

方法三：利用斜率换元.

1010

因为x1=At+x0，y1=Bt+y0，代入直线l的方程，得t=所以

方法四：构造=（x-x，y-y），n=（A，B）都是直线l的法向量，则

1010所以

上述方法“贵”在联系紧密，体现出来的是后一种方法是对前一种方法的改进与优化，呈现出来的是由繁到简、由浅及深的思维过程.虽然点到直线的距离公式的方法很多，但要明白好思路方法并不是教师强加给学生，而是通过在教师的引导下使学生“自然想到”，否则很容易演变为教师个人的“表演”.

三、升华：教师专业发展的契机

数学公式课教学的重点就更应突出公式的发现、探索和证明的过程，这一数学活动过程中蕴含着育人的价值，尤其是让学生不断探索、发现、思考、确定思路方案和具体的操作流程，不断地采取验证、完善，最后形成切实可行的点到直线的距离公式证明方法，数学公式的教学，是让学生了解和经历公式的探究过程成为思维提升、思维训练的良好素材，增强每一位学生解决问题的信心、锤炼坚强的毅力和锲而不舍的探究精神，充分发挥学生独立自主的学习能力，有利于学生长远的发展和成长.通过本课，教师可以从中提炼出一般公式课的教学策略.

1.注重知识的前后联系

数学是一门逻辑性很强、前后知识联系很紧密的学科，联系旧知识、学习新知识是学习数学的重要方法.乌申斯基有句名言：“智慧不是别的，而是组织得很好的知识体系.”数学知识的教学不是不加组织地向学生传授孤立的知识，教师要引导学生对知识间的联系加以组织和提炼.郑毓信教授也多次强调“数学教学不应求全，而要求联”.对于数学公式定理的推导来说，关注知识的前后联系，在已有的基础上学习新知，可以降低思维的难度，从而使推导过程自然流畅.

2.注重学生的个人体验

传统的课堂教学模式中，教师在规定的时间内完成事先准备的内容，注重了知识的传输，对作为学习主体的学生关注不够，因而教学效率不高，学习的效果也不好.适合学生的教学才是有效的教学，关注学生成为有效教学的前提.课前，要关注新旧知识的联系，学生是否具备学习新知识的学习条件，是否具备了学习新知的“心向”；课上，要时刻关注学生的学习状态，包括学习的反应、情绪等，对出现的问题及时处理，调整自己的教学；课后，也要关注学生的反馈，包括作业、学生问题等.教学过程中，只有对学生全程关注，才能有针对性地设计教学，才是高效的课堂，才会是高质量的教学.