水下航行器闭式循环动力系统动态仿真

白 杰, 党建军, 罗 凯, 李代金



水下航行器闭式循环动力系统动态仿真

白 杰, 党建军, 罗 凯, 李代金

(西北工业大学航海学院, 陕西西安, 710072)

为研制高能量密度无人水下航行器(UUV)动力系统, 对以Li/SF6为热源的闭式循环动力系统开展研究。基于质量守恒和能量守恒方程, 将蒸发器及冷凝器进行分区, 建立了移动边界数学模型, 建立了涡轮机的稳态模型以及集液器的动态模型, 形成了系统的动态模型。通过仿真计算, 获得了系统工质流量阶跃变化条件下的动态响应。仿真结果表明, 蒸发器进口水流量增加时, 管内压力升高, 出口温度降低, 涡轮机输出功率增大, 蒸发器及冷凝器各相区长度改变; 当其流量减小时, 变化规律相反。所建模型可为UUV动力系统设计及控制方案选择提供参考。

无人水下航行器(UUV); 闭式循环动力系统; 涡轮机; 动态模型; 移动边界法

0 引言

无人水下航行器(unmanned underwater vehicle, UUV)的性能和作用在很大程度上取决于续航能力, 动力源是其技术发展的主要瓶颈之一[1]。目前, UUV主要使用电动力推进, 具有使用简便、隐蔽性好、不受海水背压影响的优势。然而现有电池的发展技术水平, 制约了动力系统的运行时间。研究人员转向研究高密度燃料电池或热电混合动力系统, 期望应用到未来的UUV上[2-3]。

MK50重型鱼雷是闭式循环动力系统的典范。然而, 该动力系统仅适合于短时间、高功率的工况。对于需要长时间、低功率运行的轻型UUV, 容易导致反应器喷嘴堵塞, 重复启动困难[4], 因而研究人员期望设计适用于Li/SF6缓慢燃烧的反应器。

美国宾州州立大学的G.M.Faeth[4]研究团队首次提出“毛细灯芯燃烧”的概念, 通过使用类似蜡烛灯芯的吸液芯, 改变燃烧器结构, 降低反应器放热功率, 研制了“热管反应器”概念样机。美国爱荷华大学的L.D.Chen[5]等进行了Li/SF6燃烧试验, 获得了Li缓慢燃烧的燃烧规律, 对反应工况选定给出指导。印度的S. K. Dahikar[6]等采用数值计算方法, 研究了SF6在Li液中燃烧反应, 给出了燃烧反应区域长度的预测方法。哈尔滨工程大学刘晓瑜[7]等开展了Li/SF6无吸液芯的燃烧反应数值计算研究, 给出了燃烧反应温度、速度流场分布。黄庆[8]等开展了Li/ SF6的缓慢燃烧试验研究, 结果可为燃烧器及吸液芯设计提供依据。

现有研究主要集中在Li/SF6热管反应器设计及试验上, 缺乏针对闭式循环动力系统的热力计算模型, 限制了系统的研制进程。因此, 开展针对系统的热力计算建模和仿真, 获得系统变工况动态特性, 对于研制小型UUV动力系统有重要意义。

1 系统模型

1.1 系统构型

文中研究的适用于小型UUV的动力系统方案如图1所示。

锅炉内部设置金属丝网, 下端部分浸没到燃料Li中。系统启动后, 金属丝网通过毛细力将液态Li提升至反应区域, 与通入的SF6气体反应。生成的热量将锅炉反应器外侧蒸发器中的水加热至过热蒸汽状态。过热蒸汽在微型涡轮机中膨胀做功, 进而带动发电机发电, 完成能量转换过程。乏汽经过壳体冷凝器冷凝后由水泵加压进入蒸发器, 进入下一循环。反应过程中, 生成物LiF和Li2S密度大于Li, 沉于锅炉反应器中, 不需排出体外。整个动力系统能量密度高, 启动性好, 无产物排放, 不受海水深度影响, 满足小型UUV对动力系统的低输出功率和长工作时间的要求。

1.2 系统动态仿真建模策略

获得动力系统在变工况条件下的动态特性, 是提出控制策略的前提。在此之前, 需要建立稳态计算模型, 获得设计点工况参数。

动态仿真的难点是系统部件模型的建立和仿真算法的实现。建立能够反映变工况过程中工质在螺旋盘管蒸发器和冷凝器中的相变换热模型是难点所在。考虑到系统仿真速度和仿真精度, 文中采用移动边界模型法[9-13]对蒸发器及冷凝器建模。在此基础上, 联立其他各部件模型方程, 构成了一个完整的系统模型。

2 数学建模

文中,,,,,,,,,,,分别代表面积、长度、周长、比焓、质量、压强、单位长度换热功率、密度、换热系数、空隙率、滑移率、效率; 下标,,,,,,,,,,,分别代表锅炉、喷嘴、蒸发器(螺旋盘管)、进口、出口、高压区、液相、两相、气相、壁面、饱和、平均。

2.1 锅炉建模

进入锅炉内部的SF6流量, 完全反应放热功率为, 蒸发器吸收热功率, 反应器内部气体温度, 比热, 质量, 其能量平衡方程

2.2 蒸发器建模

换热器中同时存在着两相区和单相区。由于动态模型中, 各相区的长度是动态变化的, 两相区和单相区之间的分界点不易捕捉, 若采用分布参数模型对各相区分别进行网格划分, 建模过程将十分复杂; 此外, 由于两相流体和单相流体的传热和流动特性相差较大, 若采用简单的单节点集总参数模型, 即不同相区的计算模型相同, 仿真精度将难以保证[13]。

在结合二者各自特点, 采用分区集总参数方法, 将各相区的长度作为求解变量, 动态跟踪两相区和单相区之间边界位置, 对各相区分别建立移动边界模型, 且在模型建立过程中作如下简化假设: 1) 工质在换热管内为一维流动; 2) 忽略工质在换热管中的压降损失; 3) 两相区计算时采用平均空隙率理论; 4) 忽略工质和换热管的轴向导热。

对于基本的控制体, 其示意图如图2所示。沿流动方向设置坐标轴轴, 其中长度变量和是进出口截面上的坐标。

通过定截面积的控制体的1D换热问题, 存在质量连续关系

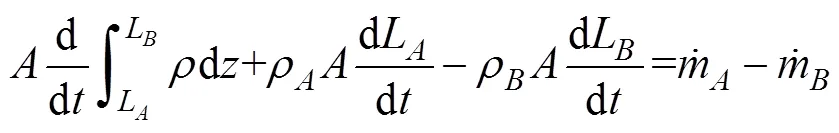
能量平衡关系

(3)

对于单相区, 平均温度为对数平均值, 两相区为饱和温度, 工质与壁面单位长度换热功率

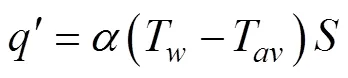
将各相区相关变量代入式(2)和式(3), 进行方程的化简。

蒸发器液相过冷区的质量守恒方程

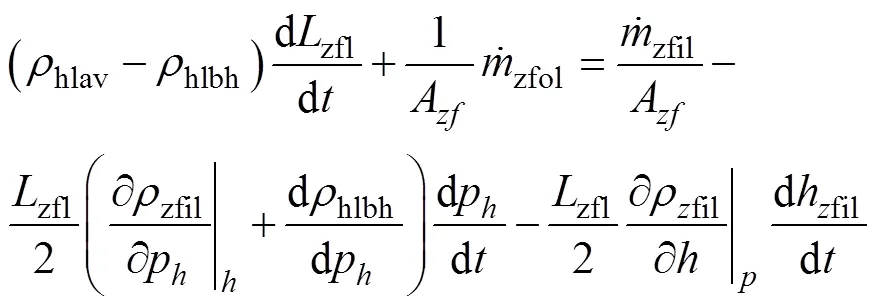
液相过冷区的能量守恒方程

(6)

两相蒸发区的平均密度

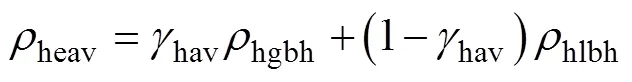
其中, 两相蒸发区的平均空隙率为

(8)

两相蒸发区中滑移率

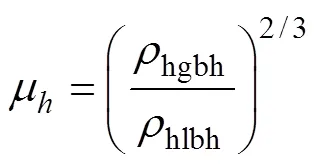
两相蒸发区的质量守恒方程

(10)

两相蒸发区的能量守恒方程

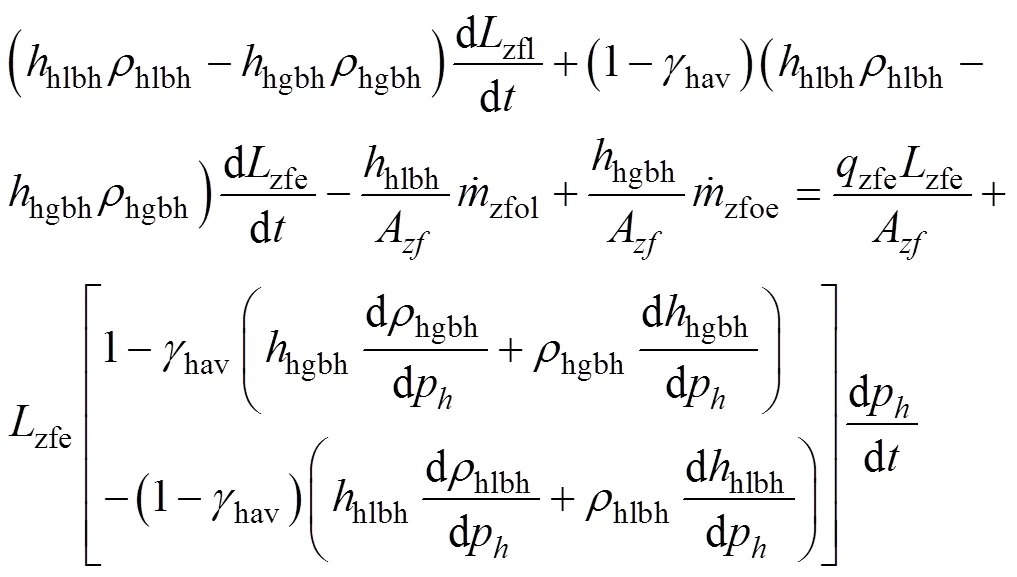
对于气相过热区, 因蒸发器的响应时间很小, 可将气相过热区按照准稳态方法处理, 其质量守恒方程

(12)

由能量守恒方程可以得出气相过热区的出口温度

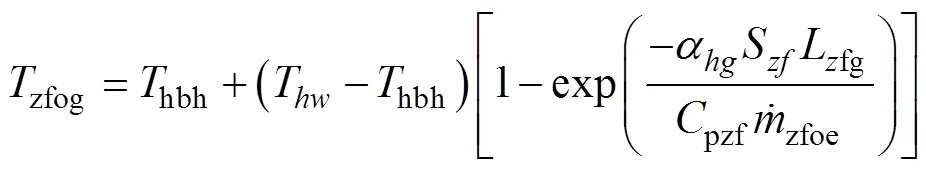
2.3 涡轮机建模

由于从系统角度仿真计算时, 并不需要准确反映涡轮机内部工作过程, 只需要求解反映主要性能的参数。另外, 该方案采用的微型涡轮机与换热器相比动态过程的时间常数较小, 所以, 可以采用稳态模型计算。

涡轮机进口参数为蒸发器出口参数, 其采用微型缩放喷嘴用于蒸汽的膨胀加速。由于喷嘴的作用, 蒸汽在喉部达到临界状态, 蒸发器出口蒸汽的流量与温度、压力存在耦合关系。

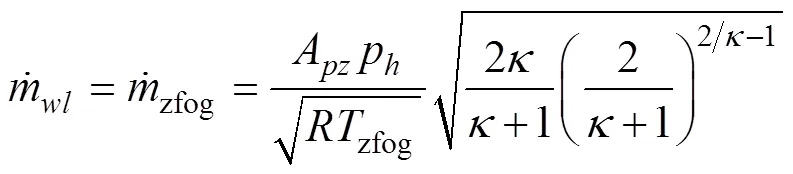
涡轮机的输出功率

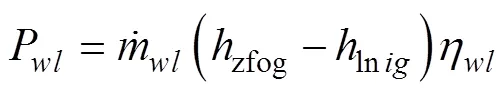
近年来2型糖尿病及其所引起的并发症的发病率明显上升，糖尿病性骨质疏松症即是一种十分常见的骨科疾病，据世界卫生组织的一项统计显示，全球目前大约有糖尿病患者3.47亿，而合并有骨质疏松症的比率为约50%～60%[1] 。当出现糖尿病性骨质疏松症后，患者发生骨折的风险明显增加，生活质量进一步下降，劳动能力减弱[2] ，故而需要积极的干预和治疗。笔者近年来采用中西医结合治疗糖尿病性骨质疏松症，取得较好的效果，现报告如下。

2.4 冷凝器建模

冷凝器与蒸发器建模方法相同, 采用式(2) ~式(4)建模, 在此不再赘述。

2.5 恒压集液器建模

恒压集液器在系统中起储存工质及缓冲作用。其质量变化关系

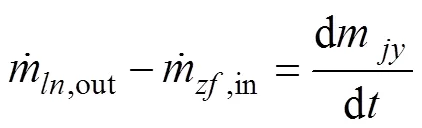
对集液器采取保温措施, 忽略其向外散热量, 其能量守恒数学模型为

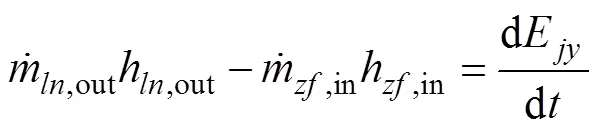
由于该系统着重研究水泵流量阶跃变化时系统的动态性能, 不研究水泵的内部工作过程, 在此不再对水泵进行建模, 系统模型建立完毕。

3 动态仿真分析

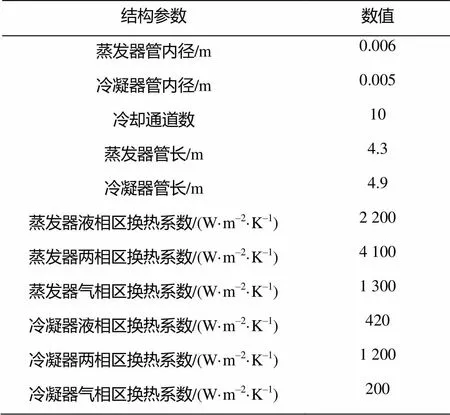
表1 仿真计算输入参数

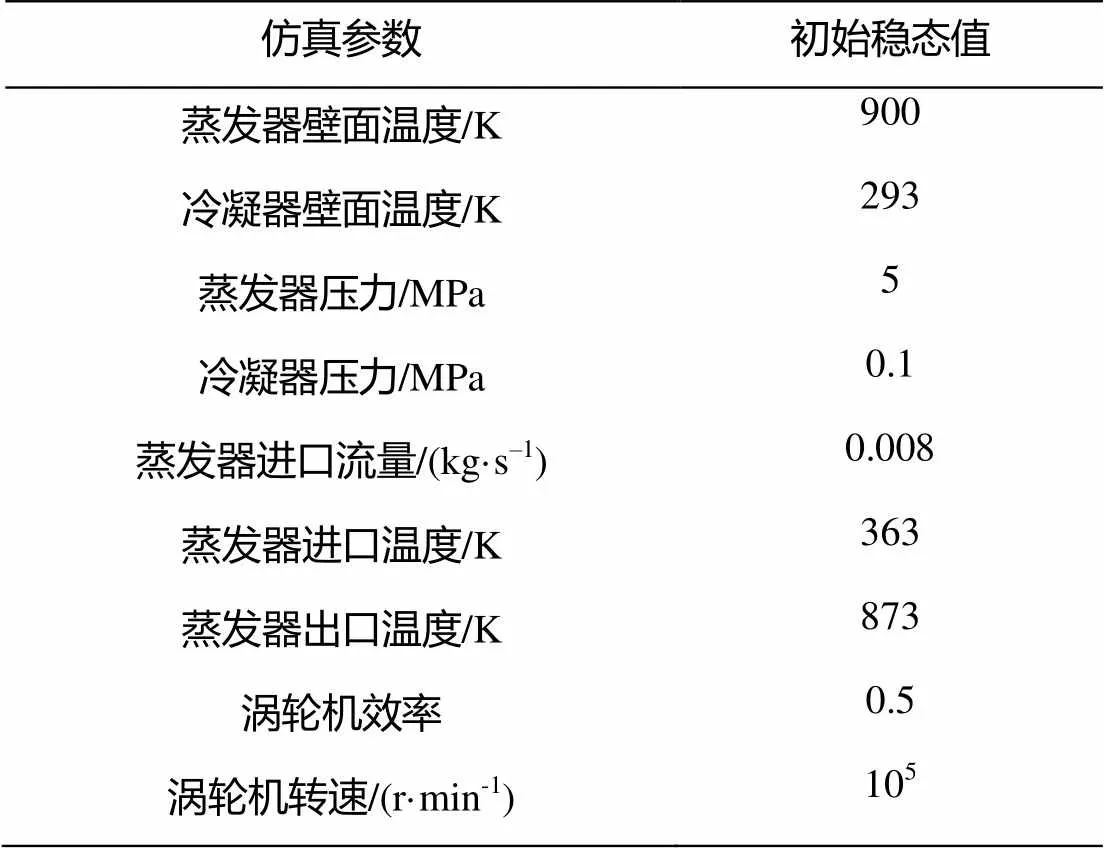
表2 仿真初始稳态值

以上仿真结果体现了变工况过程中泵流量阶跃变化时系统关键参数变化规律。当蒸发器进口水量增加时, 管内压力升高, 出口温度降低, 如图3、图4所示。这是由于液态水增加时, 工质在管内流速增加, 液相区和两相区长度增加,气相区长度变短, 如图5所示。由于增大了系统的流量, 以及涡轮机入口压强, 系统输出功率增大, 如图6所示。工质获得的热量不足以将其加热到更高的温度, 因此蒸发器出口温度降低。其导致涡轮机出口温度降低, 因此冷凝器气相区缩短, 两相区增加, 如图7所示。当水量减少时, 工质各部件处的动态变化规律相反。

以上结果表明, 该仿真模型可以对系统变工况条件下动态过程进行预测, 可为控制方案的选择及蒸发器、冷凝器等部件设计提供参考依据, 也可为系统变工况过程流量参数选定提供参考依据。

4 结束语

文中针对小型UUV用闭式循环动力系统开展研究, 应用移动边界法建立了换热器分相区集总参数数学模型, 建立了系统级动态仿真计算模型。通过仿真计算, 研究了泵流量阶跃变化条件下系统的动态响应。

结果表明, 蒸发器进口水流量增加时, 管内压力升高, 出口温度降低, 涡轮机输出功率增大, 蒸发器液相区及两相区变长, 气相区变短, 冷凝器气相区及液相区缩短, 两相区增加。蒸发器进口流量减小时, 变化规律相反。

该模型可以反映工质在系统各部件处的性能参数, 可对变工况动态过程进行性能预示, 可为动力系统的研制、优化设计提供参考依据。

[1] Gafurov S A, Klochkov E V. Autonomous Unmanned Underwater Vehicles Development Tendencies[J]. Procedia Engineering, 2015, 106: 141-148.

[2] Waters D F, Cadou C P. Estimating the Neutrally Buoyant Energy Density of a Rankine-cycle/fuel-cell Underwater Propulsion System[J]. Journal of Power Sources, 2014, 248(4): 714-720.

[3] Waters D F, Cadou C P. Modeling a Hybrid Rankine-cycle/fuel-cell Underwater Propulsion System Based on Aluminum-water Combustion[J]. Journal of Power Sources, 2013, 221(1): 272-283.

[4] Groff E G, Faeth G M. Steady Metal Combustor as a Closed Thermal Energy Source[J]. Journal of Hydronautics, 1978, 12(2): 63-70.

[5] Hsu K Y, Chen L D. An Experimental Investigation of Li and SF6 Wick Combustion[J]. Combustion and Flame, 1995, 102(1-2): 73-86.

[6] Dahikar S K, Joshi J B, Shah M S, et al. Experimental and Computational Fluid Dynamic Study of Reacting Gas Jet in Liquid: Flow Pattern and Heat Transfer[J]. Chemical Engineering Science, 2010, 65(2): 827-849.

[7] 刘晓瑜. Li/SF6表面喷射反应器内燃烧流场数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[8] 黄庆, 卜建杰, 郑邯勇, 等. 液态锂在金属丝网上的毛细作用[J]. 舰船科学技术, 2007, 29(6): 130-134. Huang Qing, Bu Jian-jie, Zheng Han-yong, et al. The Capillarity of Liquid Lithium on the Metal Screen[J]. Ship Science and Technology, 2007, 29(6): 130-134.

[9] Horst T A, Rottengruber H, Seifert M, et al. Dynamic Heat Exchanger Model for Performance Prediction and Control System Design of Automotive Waste Heat Recovery Systems[J]. Applied Energy, 2013, 105(1): 293-303.

[10] Cecchinato L, Mancini F. An Intrinsically Mass Conservative Switched Evaporator Model Adopting the Moving-boundary Method[J]. International Journal of Refrigeration, 2012, 35(2): 349-364.

[11] Ding X, Cai W, Duan P, et al. Hybrid Dynamic Modeling for Two Phase Flow Condensers[J]. Applied Thermal Engineering, 2014, 62(2): 830-837.

[12] Bonilla J, Dormido S, Cellier F O E. Switching Moving Boundary Models for Two-phase Flow Evaporators and Condensers[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 20(3): 743-768.

[13] Wei D, Lu X, Lu Z, et al. Dynamic Modeling and Simulation of an Organic Rankine Cycle (ORC) System for Waste Heat Recovery[J]. Applied Thermal Engineering, 2008, 28(10): 1216-1224.

(责任编辑: 许 妍)

Dynamic Simulation of Closed Cycle Power System for UUV

BAI JieDANG JianjunLUO KaiLI Daijin

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

The closed cycle power system based on Li/SF6 heat pipe reactor is investigated for the purpose of designing high energy density power system of unmanned underwater vehicle(UUV). The moving boundary models of an evaporator and a condenser are established based on mass conservation and energy conservation equations with dividing their heat exchangers into different areas. The steady state model of a turbine and the dynamic model of a liquid trap are established. And the dynamic model of the whole system is built. With step change of the inlet water flow rate of the evaporator, the dynamic characteristics of the key components of the system are obtained by simulation. The results show that with the increase in the inlet water flow rate, the pressure in the tube rises up, the temperature at evaporator outlet decreases, the turbine power output gets higher, and the phase zone lengths of the evaporator and condenser change. When the flow rate decreases, the above behaviors change on the contrary. These models may be applicable to design of UUV power system and its control strategy.

unmanned underwater vehicle(UUV); closed cycle power system; turbine; dynamic model; moving boundary method

10.11993/j.issn.1673-1948.2016.06.008

TJ630.32; TB115

A

1673-1948(2016)06-0438-06

2016-07-22;

2016-08-25.

国家自然科学基金资助(51409215).

白 杰(1985-), 男, 在读博士, 主要研究方向为水下航行器动力技术.