鱼雷涡轮发动机转速闭环控制仿真

马 良, 杨赪石, 张孝毅, 路 骏,3, 陈 刚, 韩勇军



鱼雷涡轮发动机转速闭环控制仿真

马 良1,2, 杨赪石1,2, 张孝毅1, 路 骏1,3, 陈 刚1, 韩勇军1

(1. 中国船舶重工集团公司第705研究所, 陕西西安, 710077; 2. 水下信息与控制重点实验室, 陕西西安, 710077; 3. 西北工业大学航海学院, 陕西西安, 710072)

为实现鱼雷的大范围变速能力, 针对热动力鱼雷某型号涡轮发动机系统的非线性和大范围换速和变深中参数变化大的问题, 通过对变燃料泵、燃烧室和发动机建模, 仿真获得了系统的非线性特性和动态特性以及不同工况下的系统参数, 制定了转速闭环控制策略, 采用变参数PID控制算法, 完成了涡轮发动机转速的闭环控制仿真。仿真结果表明, 涡轮发动机的转速闭环控制性能良好。

热动力鱼雷; 涡轮发动机; 转速; 闭环控制; 变参数PID

0 引言

伴随科技发展, 热动力鱼雷发动机转速控制研究经历了由单速制、双速制向多速制和无级变速发展的过程, 其控制方式也由开环控制发展为闭环控制。活塞发动机由于最大输出功率较小, 限制了鱼雷的航速, 已不能满足鱼雷高航速的要求。而涡轮发动机具有功率大、耗气量低、焓降大等优点[1], 输出功率变化范围大, 能大幅提高鱼雷的航速, 可以实现鱼雷大范围的换速或变深[2]。但涡轮发动机是一个非线性的对象, 对工况变动特别是海水背压的变化很敏感, 深度特性差, 控制调节比较复杂。为实现鱼雷的大范围变速能力, 需对涡轮发动机转速的闭环控制进行研究。

在涡轮发动机转速的调节控制方面, 主要针对基于电控变量燃料泵的转速闭环控制开展了大量研究工作, 提出了热动力无级变速的实现方式, 并对其特性进行了仿真分析[3-5]。目前国内也完成了相关试验, 对涡轮发动机系统的调节功能和工作特性进行了初步验证和考核, 但针对的均为功率较低、变化范围较小的动力系统。

文中通过对热动力鱼雷某大功率涡轮发动机系统建模与分析, 制定了相应的控制策略和控制算法, 建立了控制系统仿真模型, 旨在通过控制参数的自动整定, 实现涡轮发动机全工况下的自动控制, 从而实现无级调速能力, 并通过仿真分析, 验证了涡轮发动机转速闭环控制的可行性, 为下一步的试验研究提供理论支撑。

1 热动力系统组成

鱼雷热动力系统的主要组成分为燃料舱、比例控制器、启动切换阀、变量燃料泵、燃烧室、发动机、推进器、转速控制器及其他辅机等部分[6]。对于文中研究而言, 动力系统主要组成可以简化如图1所示。

变量燃料泵: 实现对燃料的增压和流量调节。

燃烧室: 将燃料充分燃烧, 产生推动涡轮发动机工作的燃气。

发动机: 发动机为单级冲动式涡轮机, 实现燃气热能到动能的转变, 燃气动能到涡轮机轴机械能的转换。

推进器或负载: 采用泵喷射推进器, 提供鱼雷运动所需的推力。

转速控制器: 实现对变量燃料泵的有效、可靠控制, 保证动力系统在各工况下转速基本保持恒定。

文中主要研究变量燃料泵输出流量对涡轮发动机转速的影响, 通过控制流量来控制发动机转速。

2 热动力系统建模

2.1 变量燃料泵模型

变量燃料泵为一种斜盘旋转式轴向柱塞泵, 通过电机驱动调节机构, 改变配流角来控制泵的排量。变量燃料泵在改变排量时, 调节机构将电机的转速转化成配流角的转速, 改变配流角的大小。

变量燃料泵的流量为

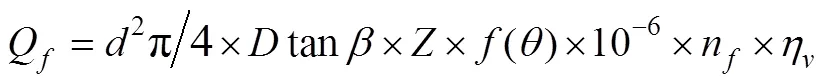
变量燃料泵的配流角由电机控制, 电机转速与配流角转速存在比例关系, 故配流角大小通过电机转速积分得到; 电机可以看作1阶惯性环节[5], 惯性很小, 分析时可以作比例环节处理。因此, 泵配流角对执行电机驱动电压的传递函数表示为

2.2 燃烧室和发动机模型

燃烧室压力

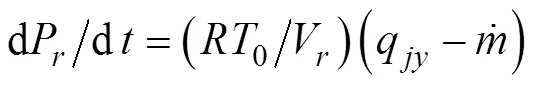
涡轮机的燃气消耗量

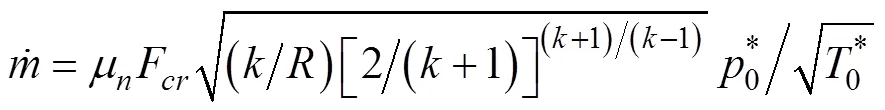
涡轮机最大可用等熵焓降

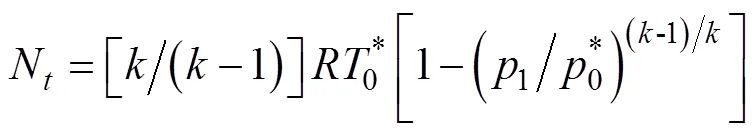
涡轮机输出的有效功率

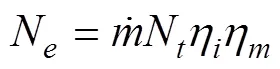
其中

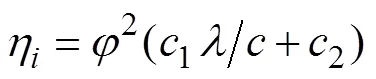
涡轮机主轴系动力学方程

根据建立的变量燃料泵模型、燃烧室和涡轮发动机仿真模型, 建立发动机转速对控制信号的仿真模型, 如图2所示。

2.3 模型验证

2.3.1 变量泵模型验证

由于泵出口压力的变化及其结构参数的影响, 泵实际排量与配流角的关系与理论关系存在一定的差异, 需要对排量与配流角的关系进行验证。图3是试验和仿真得到的泵排量与配流角大小的关系。

由图3可知, 模型与试验得到的排量与配流角关系相差较大。理论模型中未考虑出口压力、配流角等因素对容积效率的影响, 且配流盘机械结构决定了排量与配流角并非呈严格的函数关系。通过对试验数据进行拟合, 重新获得泵排量与配流角的关系, 对变量燃料泵模型中泵排量与配流角的关系进行修正。

2.3.2 燃烧室和发动机模型验证

燃烧室与发动机模型相对较复杂, 涉及燃烧、热功转换等多个环节, 是动力系统最关键的组件, 其模型准确与否直接影响到整个系统模型的准确度, 因此必须对其模型进行验证。文中所研究的涡轮发动机系统的功率试验工作仍在进行中, 没有相关试验数据。此处选用另一涡轮发动机系统进行辅助验证。

采用功率试验变速过程的数据曲线与模型仿真结果进行对比。将试验的泵体积流量数据转换为质量流量数据作为模型的输入, 得到燃烧室压力和涡轮发动机转速仿真结果, 对比结果如图4和图5所示。

由图4和图5可知, 仿真结果与试验数据基本一致, 验证了仿真模型的准确性。其中, 燃烧室压力试验曲线表示的是燃烧室的头压, 仿真曲线表示的是燃烧室的压力, 两者差表示燃烧室喷嘴的压降, 与实际情况接近。

2.4 模型分析

燃烧室: 根据式(3)和式(4), 得到燃烧室压力的传递函数

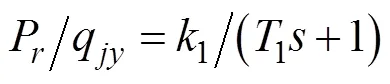
发动机: 涡轮发动机的数学模型相对较为复杂, 不容易直接对其进行分析。文中采用系统辨识技术对发动机进行特性分析[8], 在不同工况条件下, 选择惯性环节模型方法进行参数辨识, 拟合度达到了95%以上。结果表明, 涡轮发动机转速对燃烧室压力的响应为惯性环节[9], 惯性环节参数通过系统辨识获得, 时间参数为。

以上分析可知, 涡轮发动机转速对燃烧室压力的响应可以看作惯性环节;>>, 燃烧室压力对泵供流量的响应速度快, 远高于涡轮发动机转速对燃烧室压力的响应速度, 可近似看作比例环节。故涡轮发动机转速对泵供流量的响应可以认为是惯性环节, 其传递函数

式中,k为惯性环节增益。

鱼雷在换速或变深等变工况下工作时, 涡轮发动机主要工作参数会发生大范围变化, 进而引起惯性环节参数的变化。为获得惯性环节的参数, 对燃烧室与涡轮发动机的仿真模型进行不同工况下的仿真, 再采用系统辨识技术对参数进行辨识, 得到了不同工况下惯性环节的参数。仿真结果表明, 时间参数变化较小, 可以取定值且增益参数变化较大。

3 转速闭环控制策略

3.1 控制策略讨论

涡轮发动机转速的控制是通过控制伺服电机, 改变燃料泵配流角, 从而改变泵的排量, 进而改变燃料泵的输出流量以控制涡轮发动机的转速。控制量的选取具有以下几种方案。

1) 燃料泵输出流量作为控制量

泵输出流量除以检测得到的发动机转速后, 转换成配流角信号, 对配流角进行闭环控制, 其工作流程如图6所示。该方法存在的主要问题: 发动机转速对泵供流量具有惯性, 给系统带来一定的影响。对模型进行仿真分析可知, 发动机转速对泵供流量不再是惯性环节, 该方法加大了系统的复杂性, 加大了控制的难度。

2) 泵配流角作为控制量

对配流角进行闭环控制, 其工作流程如图7所示。该方法存在的主要问题: 配流角闭环控制环节可以表示为惯性环节, 且要求其惯性常数较小, 以满足变速时配流角的快速响应, 而配流角执行电机转速的饱和特性对配流角闭环控制环节存在一定影响, 加大了该环节的非线性, 影响了整个控制系统局部的动态特性。

3) 电机的控制电压作为控制量

泵执行电机的驱动电压直接作为控制量, 配流角由电压积分获得, 其工作流程如图8所示。电机转速的饱和特性对控制系统虽然会产生影响, 但其不会影响控制系统局部的动态特性, 从而在整个控制系统中产生的影响较小。

综上所述, 文中采用第3种方案, 即电机的控制电压作为控制量。

通过模型的建立、分析和控制策略的选取, 最终得到发动机转速闭环控制的控制模型, 如图9所示。

图9中，in和out分别表示输入和输出涡轮机转速;表示转速偏差;表示泵执行电机的驱动电压; theta表示泵配流角;表示泵输出流量;表示泵供流量与配流角的比值, 其随系统工况变化而变化, 且与发动机转速成正比, 通过系统仿真可以获得在不同工况下的取值。

3.2 控制策略分析

如图7所示, 系统闭环传递函数为

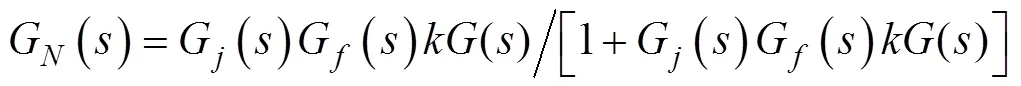
期望闭环传递函数为1阶惯性环节, 即

(12)

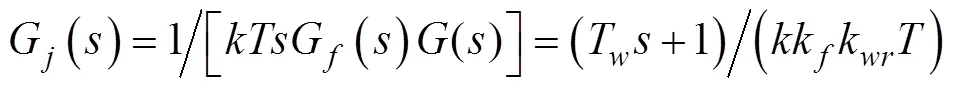
此时泵供流量的闭环传递函数为

(14)

故而, 初步得到控制律传递函数

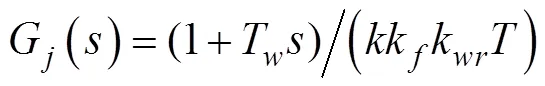
下面对该传递函数的参数和存在的问题进行分析。

图10为不同深度下, 发动机转速及其对应的泵配流角的关系曲线, 其比值为与的乘积。

由图10可知, 相同转速下, 配流角随着深度增大而增大; 相同深度下(除外), 配流角基本随着转速增大而增大;深度下, 相对转速在60%左右时配流角最小, 且随着转速增大或减小, 配流角均增大。

2) 微分项系数的修正

在发动机转速的闭环控制模型中, 将泵供流量与配流角的关系用静态的比值表示, 而实际泵供流量与发动机转速关系密切, 发动机转速响应的快慢很大程度上影响了泵供流量对配流角这个过程的惯性, 实际配流角到发动机转速的响应时间可以通过系统辨识技术得到, 响应时间>。

根据以上分析, 调整控制律传递函数中的相关参数, 以期获得控制性能更好的传递函数。

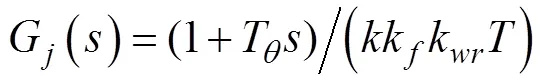
(17)

闭环传递函数为

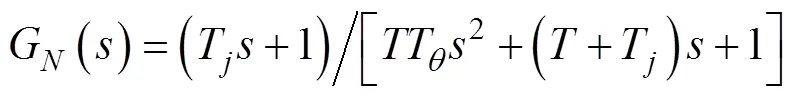
闭环控制系统为2阶系统, 系统稳定。

极点为

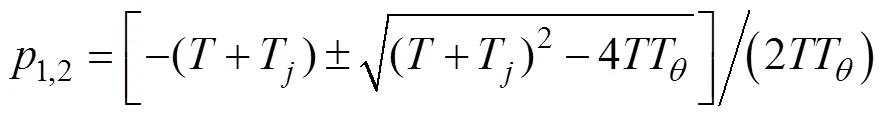
零点为

(20)

系统输入为转速信号, 可以看作阶跃输入。

此时配流角闭环传递函数为

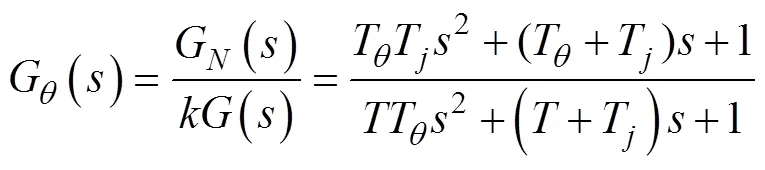
同理, 配流角相对系统输入稳定。故而, 最终得到控制律传递函数

(22)

3.3 控制算法设计

由控制律传递函数的形式可知, 该传递函数可以由PID调节实现。由于系统参数随着工况发生变化, 控制律传递函数的参数也将发生变化,故文中采用变参数PID控制算法来实现控制律传递函数[10]。

至此, 整个控制系统的仿真模型搭建完毕, 如图11所示。

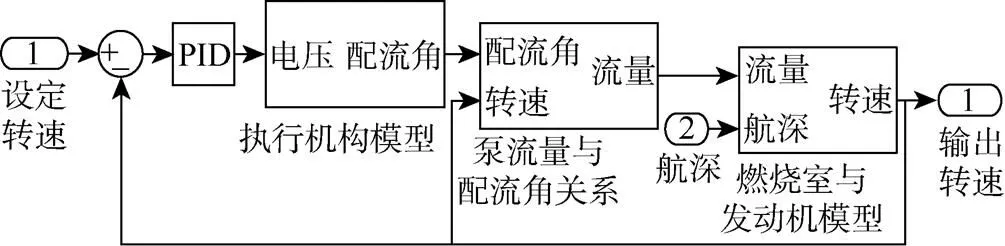
图11 控制系统的仿真模型

4 仿真结果与分析

对搭建的控制系统模型进行仿真, 图12和图13分别是某深度下换速和某航速下变深的仿真结果曲线。

由图12可知, 当鱼雷进行换速时, 发动机换速平稳, 且转速不存在超调, 换速时间满足预设要求; 燃烧室压力、配流角和泵供流量变化平稳, 不存在超调; 控制信号良好。

由图13可知, 当鱼雷进行变深时, 发动机转速发生变化, 转速偏差不大于2%, 转速调节时间短, 调节速度快; 燃烧室压力、配流角和泵供流量变化平稳, 不存在超调; 控制信号良好。

由换速和变深仿真结果可知, 选择电机控制电压作为控制量的策略, 采用PID控制算法, 可以实现鱼雷热动力涡轮发动机的转速闭环控制。

5 结束语

文中通过对热动力鱼雷涡轮发动机系统进行建模与仿真分析, 获得了热动力系统的非线性特性和动态特性, 讨论了不同控制策略的影响, 制定了以变量燃料泵配流角执行电机的控制电压作为控制量的控制策略, 采用变参数PID控制算法, 进行了控制系统仿真。仿真结果表明, 在鱼雷换速或变深条件下, 闭环控制算法可以实现对涡轮发动机转速的控制, 且控制性能良好, 为下一步的试验研究提供了参考。

[1] Osborne G F. The Spearfish Propulsion System[J]. GEC Review, 1998, 13(3): 150-162.

[2] 郑直飞, 史小锋, 伊寅, 等. 燃气涡轮机在鱼雷动力系统中的应用与发展[J]. 鱼雷技术, 2006, 14(4): 11-15.Zheng Zhi-fei, Shi Xiao-feng, Yi Yin, et al. Development and Application of Gas Turbine to Torpedo Power[J]. Torpedo Technology, 2006, 14(4): 11-15.

[3] 种衡阳, 王育才, 刘剑钊, 等. 变工况条件下鱼雷涡轮发动机控制方法[J]. 火力与指挥控制, 2010(s1): 102-104.Zhong Heng-yang, Wang Yu-cai, Liu Jian-zhao, et al. Research of Torpedo Turbine Control Under Non-design Conditions[J]. Fire Control and Command Control, 2010(s1): 102-104.

[4] 李淼, 罗凯, 胡峰, 等. 水下涡轮发动机推进系统闭环控制设计[J]. 计算机测量与控制, 2011, 19(9): 2180-2182

Li Miao, Luo Kai, Hu Feng, et al. Design of Speed Closed-loop Control for Underwater Turbine Engine Propulsion System[J]. Computer Measurement & Control, 2011, 19(9): 2180-2182.

[5] 罗凯, 张学雷, 王晓欣, 等. 水下涡轮机系统转速闭环控制研究[J]. 鱼雷技术, 2015, 23(1): 44-48.Luo Kai, Zhang Xue-lei, Wang Xiao-xin, et al. A Closed-loop Rotary Velocity Controller for Underwater Turbine Propulsion System[J]. Torpedo Technology, 2015, 23(1): 44-48.

[6] 韩勇军. 鱼雷涡轮机系统启动机变工况过程仿真[D]. 北京: 中国舰船研究院, 2010: 11-15.

[7] 罗凯, 党建军, 王育才. 水下热动力推进系统自动控制[M]. 西安: 西北工业大学出版社, 2005.

[8] 张孝毅. 基于压力调节的鱼雷热动力转速闭环控制研究[D]. 北京: 中国舰船研究院, 2012: 14-16.

[9] 倪博溢, 萧德云. MATLAB 环境下的系统辨识仿真工具箱[J]. 系统仿真学报, 2006, 18(6): 1493-1496.Ni Bo-yi, Xiao De-yun. System Identification and Simulation Toolbox under MATLAB Environment[J]. Journal of System Simulation, 2006, 18(6):1493-1496.

[10] 乔宏, 伊寅, 师海潮. 变参数PID方法在涡轮机闭环控制上的应用研究[J]. 鱼雷技术, 2009, 17(1): 40-43.Qiao Hong, Yi Yin, Shi Hai-chao. Application of Variable- Parameter PID Control to Closed Loop Control for Torpedo Turbine Engine[J]. Torpedo Technology, 2009, 17(1): 40-43.

(责任编辑: 许 妍)

Simulation on Closed-loop Control of Torpedo Turbine Rotary Velocity

MA Liang,YANG Cheng-shi,ZHANG Xiao-yi, LU Jun,CHEN Gang, HAN Yong-jun

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710077, China; 3. School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

To realize speed variation of a torpedo in a wide range, the nonlinearity and the remarkable variation of parameters due to the speed and depth variations in wide range are considered for a certain type of turbine engine system of thermal propulsion torpedo. The models of fuel-variable pump, combustion chamber and engine are established to obtain the nonlinear and dynamic characteristics of the system as well as the system parameters in different conditions. Further, a closed-loop control strategy of rotary velocity is drawn up, and the proportion-integral-derivative(PID) control algorithm with variable parameters is adopted to implement rotary velocity control simulation of the turbine engine. Simulation results indicate good performance of the closed-loop control of turbine engine rotary velocity.

thermal propulsion torpedo; turbine engine; rotary velocity; closed-loop control; proportion-integral-derivative(PID) control with variable parameter

10.11993/j.issn.1673-1948.2016.06.007

TJ630.32；TP271.7

A

1673-1948(2016)06-0431-07

2016-09-23;

2016-10-19.

马 良(1992-), 男, 在读硕士, 主要研究方向为能源动力推进技术.