自适应滤波算法分析及仿真

于新颖

(山西大学商务学院 信息学院，山西 太原 030031)

自适应滤波算法分析及仿真

于新颖

(山西大学商务学院 信息学院，山西 太原 030031)

主要对自适应滤波算法展开了研究和讨论，重点对LMS算法、NLMS算法以及RLS算法做了详细的说明和对比，在算法原理、算法性能分析方面说明了各自算法的优越性。通过MATLAB仿真，对每种算法的收敛性、学习曲线和误差分析等方面进行了分析。

自适应；噪声对消；LMS算法；NLMS算法；RLS算法

由于真实客观环境中噪声的特性常常是不平稳的，因而自适应滤波在噪声对消中的应用有着广阔的发展前景。随着自适应噪声对消技术的发展，应用于自适应噪声对消系统的算法也发生了很大的变迁。其中最常用的是LMS(最小均方算法)和RLS(递归最小二乘算法)，而LMS算法[1]以其算法简单，运算量小，实现容易等优点而得到了广泛应用，但固定步长的LMS算法在收敛速率，跟踪速率和权失调噪声要求方面存在矛盾；为了解决这一矛盾，人们研究出了变步长的LMS算法。但基于变步长LMS的算法存在收敛特性和失调量受步长影响的缺点，且最优步长不太容易确定，因此NLMS，ELMS等关于LMS的改进的滤波算法得到了发展。RLS这种算法是对输入信号自相关的矩阵求逆，进而不断递推估计实现权值更新的，具有更快的收敛速度，但这种算法计算起来较为复杂，存储量大，不适用于实时性要求高的场合；另外一个使用局限是，输入信号自相关的矩阵求逆之后必须具有正定性，否则会引起算法发散。

1 算法介绍

1.1 最小均方(LMS)算法

LMS算法是随机梯度算法家族中的一员，简单性是它的一个显著特点，而且它不需要计算有关的相关函数，也不需要矩阵求逆运算，因此它也是线性自适应滤波算法的参考标准[2]。

LMS算法采用的是一种瞬时估计，即用n时刻的平方误差性能函数|e(n)|2作为瞬时均方误差ξ=E[e2(n)]的估值，其实质是以当前输出误差、当前参考信号和当前权系数求得下个时刻的权系数。

LMS算法输出信号y(n)、输出误差e(n)及权系数W(n)的计算公式为：

y(n)=W(n)XT(n) .

(1)

e(n)=d(n)-y(n)=d(n)-W(n)XT(n) .

(2)

W(n+1)=W(n)+2μe(n)X(n) .

(3)

其中μ是控制自适应速度与稳定性的增益常数,称为步长因子，选择时，应该综合考虑收敛速度和稳态误差的要求。

自适应滤波器收敛的条件是：

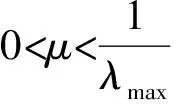
LMS算法的优点是结构较为简单，适应变化能力强，但其则具有收敛的速度较慢的缺点。为了能适用于信号实时性处理的场合，如何提高LMS这种算法的自适应速度就显得尤为重要。

局限LMS算法收敛这一要素的主要原因有：

1) 步长因子不能过大，不然算法最终不收敛；

2) 收敛速度及均方误差不能兼得。

这两个原因都与步长有关，LMS算法中的步长是唯一能够控制算法迭代过程的参量，必然是改进LMS算法性能的唯一着手点。

1.2 归一化最小均方(NLMS)算法

LMS算法是通过对梯度矢量各分量单个数据取样值的估计得到的，没有进行平均，才会使梯度估计中存在着噪声。NLMS引入变步长的迭代过程[3]，加快了收敛速度。

NLMS算法的输出信号y(n)、输出误差e(n)及权系数W(n)的计算公式为：

y(n)=W(n)XT(n) .

(4)

e(n)=d(n)-y(n) .

(5)

(6)

此即归一化LMS算法，其步长被输入信号的范数平方除，因而较LMS算法具有更好的稳定性和收敛性。

1.3 递归最小二乘(RLS)算法

RLS算法是一个递归实现，其收敛速率比一般的LMS滤波器快一个数量级，因此它在线性自适应滤波器中应用非常广泛[4]。

RLS算法的输出信号y(n)、输出误差e(n)及权系数W(n)的计算公式为：

y(n)=WT(n-1)X(n) .

(7)

e(n)=d(n)-y(n) .

(8)

W(n)=W(n-1)+g(n)[d(n)-X(n)WT(n-1)] .

(9)

其中，增益矢量g(n)=C(n-1)X(n)/[λ+XT(n)C(n-1)X(n)]；C(n)为自相关矩阵Rxx(n)的逆矩阵，其定义式为C(n)=λ-1[C(n-1)-g(n)XT(n)C(n-1)]，且C(0)=δ-1I(I为单位矩阵，δ为小的正实数)；常数λ是遗忘因子，要求0<λ≤1。

RLS算法主要应用于系统辨识、自适应控制和自适应信号处理等领域。主要优点是收敛速度快，因此在快速信道均衡、 实时系统辨识和实际序列分析中得到广泛的应用[4]，其主要缺点是每次迭代计算量大。

2 自适应算法的MATLAB仿真

2.1 LMS算法的MATLAB仿真

输入为正弦信号与随机噪声的迭加，随机噪声的幅值小于1，在取不同步长情况下，LMS算法的误差函数曲线如图1所示，误差函数图中纵坐标表示误差的大小。

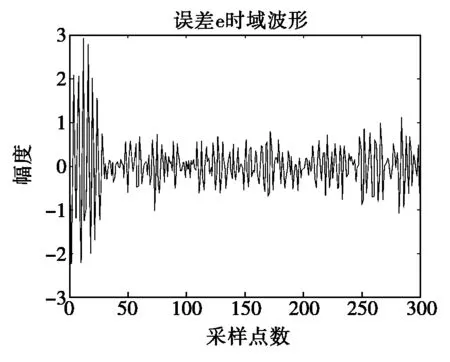
(a) u=0.03,N=300,k=16

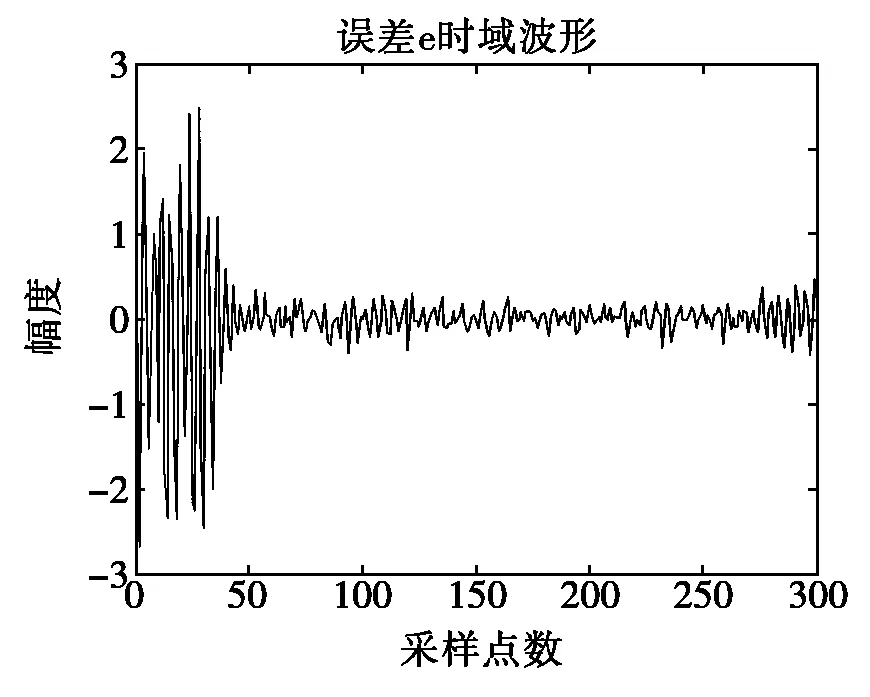
(b) u=0.03,N=300,k=32

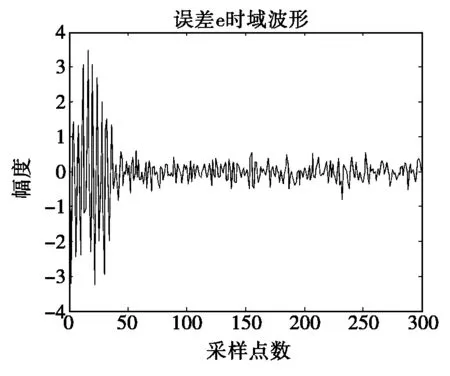
(c) u=0.05,N=300,k=32

2.2 NLMS算法的MATLAB仿真

1) 输入为正弦信号与随机噪声的迭加，随机噪声的幅值小于1。NLMS均值曲线图仿真结果如图2所示。每个图中的横坐标都表示迭代次数，学习曲线中纵坐标表示均方误差的大小。

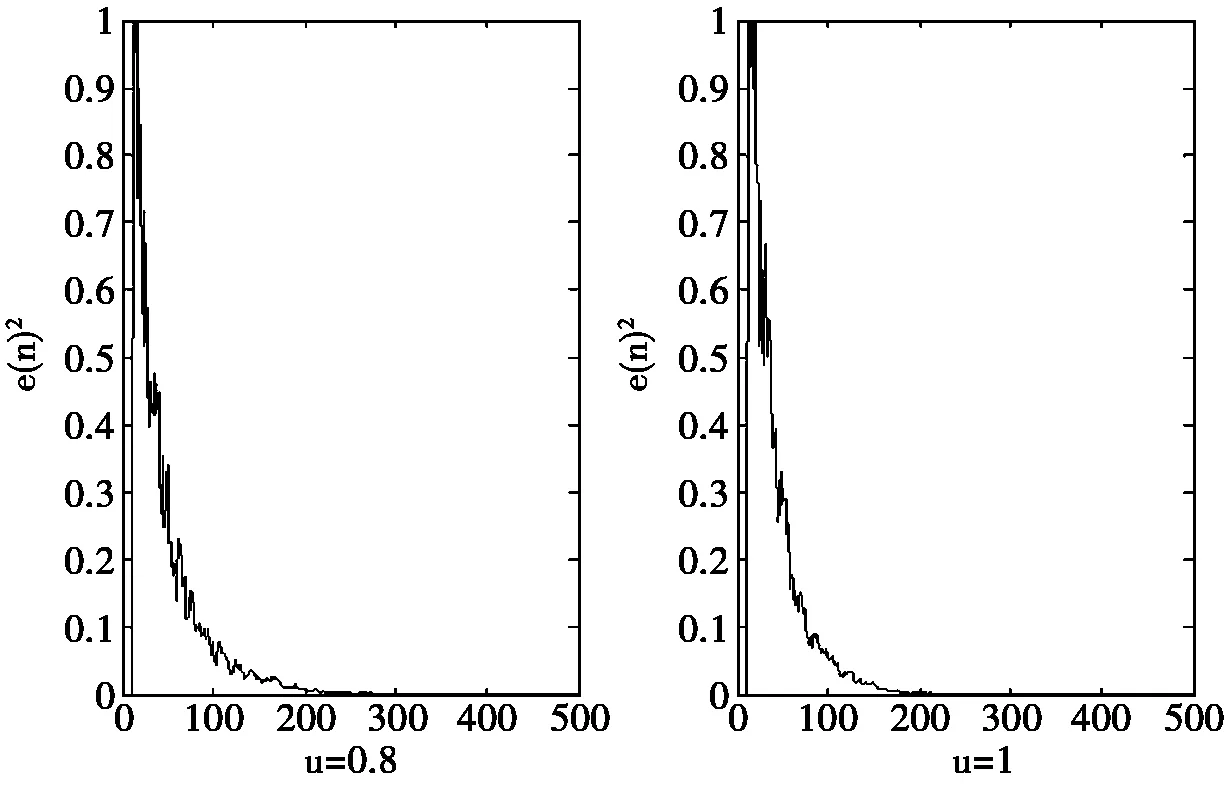
图2 NLMS算法u=0.8和u=1学习曲线

2) 当输入信号为正弦函数与噪声的叠加时，LMS和NLMS的性能对比如图3所示。

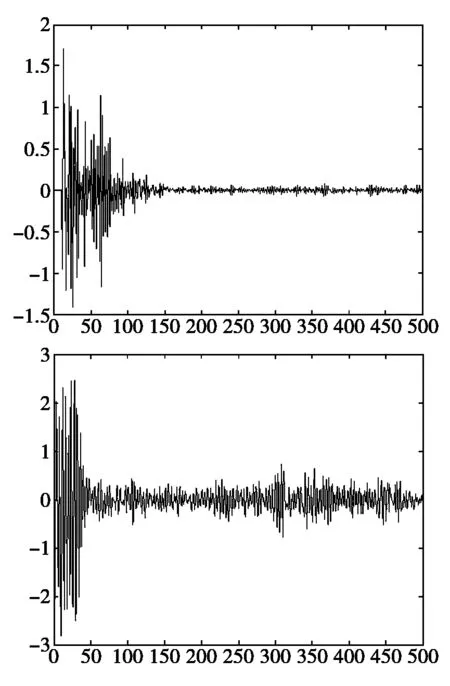
图3 LMS和NLMS算法的误差比较

2.3 RLS算法的MATLAB仿真

仿真采用多权的自适应横向滤波系统，期望响应是一个经过滤波的高斯随机噪声，采用RLS算法的自适应滤波学习曲线和矢量估计误差曲线如图4所示。

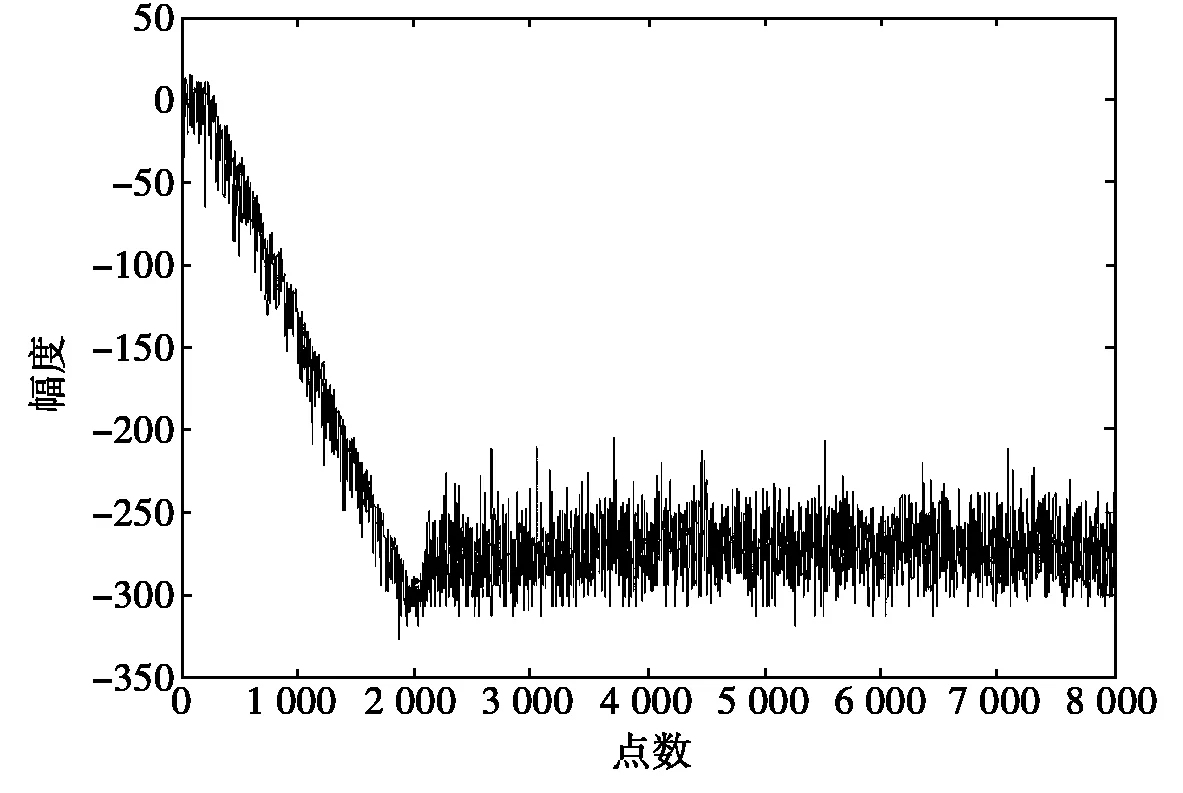
(a) RLS算法的学习曲线

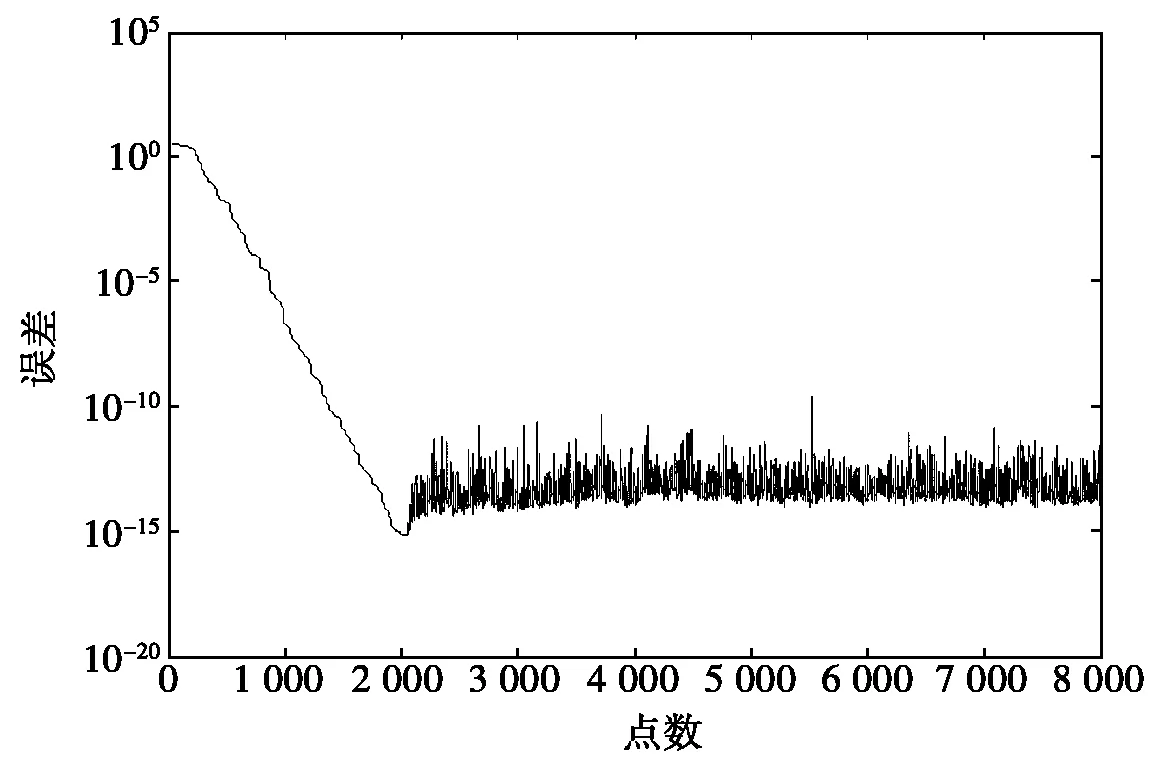
(b) RLS算法的误差曲线

3 结果分析

1) LMS算法最大的优点是易于实现，而且对有限寄存器长度造成的实现误差不敏感，在实际生活和生产中应用较为广泛。

由图1三组不同情况下LMS算法的误差图的对比可以看出，开始时误差比较类似于正弦函数，随着自适应过程的进行，误差越来越小并且随机性增大，随着迭代次数的增加逐渐趋于零附近。由图(b)、图(c)比较可知，u越小，收敛速度越慢，但稳态误差较小；由图(a)、图(b)比较可知，阶数k越小，收敛越快，但稳态误差较大。从而验证了在迭代收敛过程中，误差函数随着迭代次数的增加逐渐趋于零，学习曲线也趋于在附近小幅度波动，甚至为零。但是LMS算法的收敛速度和其稳定性能是相互矛盾的；步长较大时收敛速度较快，但其稳定性较差；步长较小时收敛速度较慢，但其稳定性较好。

2) 由图2可知，u越大，曲线收敛的越快，越容易趋于零，但曲线却更不光滑，振荡较大，符合NLMS算法的规律。另外，在NLMS算法中，当u太大时，学习曲线反而会发散；克服了LMS算法的缺点，算法本身可看成是一种变步长的自适应算法，它的步长大小与输入信号的信噪比有关。

3) RLS算法在收敛速度和信号稳定性方面的性能都比LMS和NLMS算法良好，收敛速度比LMS算法快一个数量级，收敛性能与输入信号的频谱特性无关而且对信号的跟踪能力较强，误差较小。但是RLS算法涉及到矩阵求逆，计算复杂度很高，所需的存储量极大，不利于实时实现[5]。

4 结论

本论文主要介绍了三种常用的自适应算法：LMS、NLMS及RLS，并通过MATLAB仿真，从收敛性、误差函数和学习曲线等方面对这三种算法进行了简单的分析。结果表明，LMS算法易于广泛的应用，但步长因子存在难以调和的矛盾；NLMS在收敛速度上有了明显的改进，是对于LMS的优化；RLS收敛速度和稳定性都很好，但计算量过大，不利于大范围推广。

[1] 王海峰,陈伟,黄秋元.基于LMS算法自适应噪声抵消器的分析研究[J].计算机与数字工程,2009,37(3):85-87.

[2] 秦彦平.基于DSP地下漏水定位系统的自适应滤波器设计[D].内蒙古大学，2010.

[3] 文静,文玉梅,李平.基于噪声白化准则的自适应噪声抵消方法[J].仪器仪表学报,2010,31(8):1693-1698.

[4] 肖林.LMS和RLS算法的研究与实现[J].中山大学研究生期刊，2010,31(2):73-81.

[5] 余慧.基于DSP反馈自适应噪声抵消器研究与设计[D].湖南大学,2010.

The Analysis and Simulation of Adaptive Filtering Algorithms

Yu Xinying

(SchoolofInformation,BusinessCollegeofShanxiUniversity,TaiyuanShanxi030031,China)

This paper mainly makes a study and discussion about the algorithms of adaptive filtering. It focuses on the detail description and comparison of the LMS algorithm, NLMS algorithm and RLS algorithm, shows the superiority of each algorithm through the principle and performance. With the help of MATLAB simulation, this paper analyzes the convergence, learning curve and error analysis of each algorithm.

adaptive; noise cancellation; LMS algorithm; NLMS algorithm; RLS algorithm

2016-08-24

于新颖(1987- )，女，河北唐山人，助教，硕士研究生，自适应信号处理方向。

1674- 4578(2016)06- 0007- 02

TP701

A