数形结合，提升学生数学素养

唐建军●

江苏省兴化市中堡中心校(225779)



数形结合，提升学生数学素养

唐建军●

江苏省兴化市中堡中心校(225779)

数形结合是数学思想中一种重要的解题思想，它是指在一定条件下将数与形之间进行相互转化的过程，帮助解决一些较难的问题.教师可从以数化形、以形变数和形数互变等角度渗透数形结合思想，拓宽学生的思维空间.

初中数学；数学素养；数形结合；提升策略

在初中数学教学中，教师要做的不是教给学生题目的答案，而是解题思路和数学思想.数形结合是数学思想中一种重要的解题思想，它是指在一定条件下将数与形之间进行相互转化的过程，帮助解决一些较难的问题.那么，如何在初中数学教学中巧妙地运用数形结合思想呢？

一、以数化形，理解函数图象

函数是初中数学中十分关键的一部分，它的比重十分大，许多学生在学习时感到有些困难.由于图象相比于数字而言更加形象直观，因此教师在教学这一部分内容时要结合一些图象来辅助学生进行更好的理解.

为了让学生更加容易理解y=ax2+bx+c这个式子的含义，我是这样引导学生的：我给出学生一个简单的二次函数式：y=x2-2x+1，让学生们计算出x分别为-2、-1、0、1、2、3、4时y的值，并试着画出它的图象，在画图的过程中发现这个函数的图象是一条抛物线，因此，我便利用这个函数图象引导学生进行接下来的学习， 在这个图象中，它的对称轴为x=1，与x轴有一个交点(1，0)，并且它的开口是朝上的.我又举出了几个其他的函数式子让学生们画出其图象，经过分析发现，当a>0时抛物线开口向上，当a<0时抛物线开口向下，同时图象的对称轴都可以用x=-b/(2a)来表示.在学生们掌握了这个知识点之后，我进一步以a为分析对象，对二次函数图象特点进行了深入的研究.我给出了这样几个式子：y=x2-4x+6、y=2x2-4x+6、y=2x2-4x+6、y=4x2-4x+6，让学生取几个任意x的值，代入到这几个函数中分别计算，并画出图象.经过对比发现，当正数a越大，图象的开口越小，同理，当a为负数时，a越大，开口越大.由此得出结论：|a|越大，抛物线的开口越小.

在这个过程中我们可以看出，函数的学习离不开函数图象，巧妙地运用数形结合思想，将枯燥的式子转化成图象，让学生不再局限于数字的框架中，促使学生对函数中的含义有一个更加深刻的理解.

二、以形变数，探究勾股定理

在数学的学习中，几何是继函数之后另一十分重要的内容，在这一块的内容中，勾股定理是一个基础的定理.因此，教师要加强这一定理的学习，方便学生在后续几何知识中的学习.

在教学勾股定理时，我采用了数形结合的形式来引导学生进行学习.让每个学生在自己的草稿纸上画出一个边长分别为3、4、5的直角三角形，经过计算发现32+42=52,,借此引出勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方，即：a2+b2=c2.有学生对于这个定理提出了疑问：“老师，会不会有的直角三角形不满足a2+b2=c2呢？是只有直角三角形才满足吗？其他的三角形可以吗？”带着这个疑问，我让学生随意在纸上画出几个直角三角形、锐角三角形或者钝角三角形，测量其边长再进行计算发现任意的直角三角形都满足这个定理，而钝角三角形或锐角三角形中都有a2+b2≠c2，即不满足勾股定理，验证了这个定理的唯一性.我引导学生在平常做习题时，遇到有关直角三角形求其中任意一边或是求证直角三角形的题目，不必将画出三角形，可以直接结合勾股定理进行求解和证明.在这个过程中，我将图形的特点转化成数字之间的关系，便于学生的记忆.

在数学学习的过程中，遇到一些较为复杂的几何题目时，可以将题目中的图形的条件转化为数字条件，图形与数字相互结合，更加有助于题目的解答.

三、形数互变，强化实际应用

数学来源于生活，应用于生活.在数学学习中，不仅会遇到简单的数学问题，还存在着许多复杂的实际问题.这时就需要学生在这个过程中不断在图形和数字之间进行转化，从而使问题得到解决.

例如在初中数学中有这样一类经典的题目：利用不等式关系分析比赛.在以往的教学中，教师会选择进行一步步的推理得出最终的结果，其实利用数形结合会更加简单.假设有a、b、c、d、e五个队进行单循环足球比赛，争夺出线权.比赛规则为：胜一场有2分、平一场有1分、负一场没有分，即零分.名次在前两个队出线，比赛结束后，a的积分为6分，试问只有一个队为全胜时，a队能否出现？经过分析我们发现，在这一个组中一共要进行10次比赛，a的成绩为3胜0平1负，我们假设b是全胜，画出如下的图形.

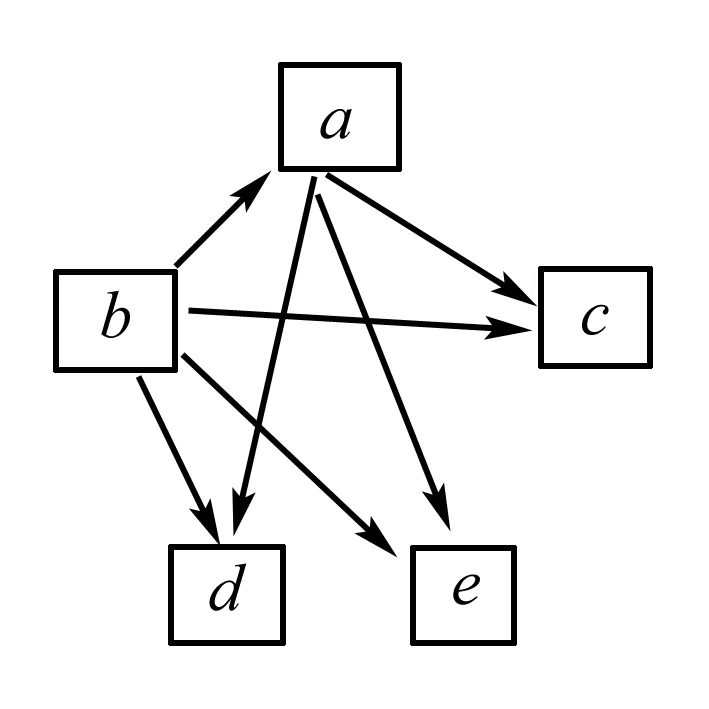
在这个图形中，箭头方向所指的一方代表了输的一方，例如a→c代表a赢了c.通过对图形进行分析，我们可以很容易地看出c、d、e之中最多能赢两场，即得4分.由此我们可以看出，不管如何，a都是前两名，即a可以出线.通过这样的分析，学生们很轻易地就能理解这道题目，变得简单了许多.

在数学的学习过程中，像这样的题目还有很多，我引导学生要深入体会数形结合思想的精髓，学会灵活变通地使用这个数学思想，使之在做题中有一个更加清楚明了的解题思路.

[1]黄雪琴.数形转化易理解,结合运用促提升[J].数学教学通讯,2013(12).

[2]杨艳丽.数形结合思想在初中数学教学中的渗透探究[J].教育实践与研究, 2011(5).

G632

B

1008-0333(2016)35-0027-01