高中数学重要的思想方法
——函数与方程思想
江苏省淮阴师范学院附属中学 窦剑眉
高中数学重要的思想方法
——函数与方程思想
江苏省淮阴师范学院附属中学 窦剑眉
函数与方程思想是高中数学中一种重要的思想方法,也是高考考查的重要思想方法之一。 函数与方程思想以函数知识做基石,用运动变化的观点分析、研究数学对象间的数量关系,使函数知识的应用得到极大的扩展,丰富并优化了数学解题活动,给数学解题带来很强的创新能力。 因此,函数与方程思想越来越成为数学高考中长考不衰的热点。
函数思想;方程思想;转化;应用
函数与方程思想就是高中数学的常用思想方法之一,也是历年高考长考不衰的热点。函数思想与方程思想的联系十分密切,解方程f(x)=0,就是求函数y=f(x)当函数值为零时自变量x的值;求综合方程f(x)=g(x)的根或根的个数,就是求函数y=f(x)与y=g(x)的图像的交点或交点个数;参数方程更具有函数因素,属于能随参数的变化而变化的动态方程。它所研究的数学对象已经不是一些孤立的点,而是具有某种共性的几何曲线。 正是这些联系,促成了函数与方程思想在数学解题中的互化互换,丰富了数学解题的思想宝库。
下面我将结合平时的教学实践,对“函数与方程”在解题中的运用及其求解策略进行初步分析,以期起到抛砖引玉的作用。
一、 函数与方程思想在应用时的相互转化
例1 如果方程cos2x-sinx+a=0在(0,]上有解,求a的取值范围。
【分析】:可分离变量为a=-cos2x+sinx,转化为确定的相关函数的值域。
解法一:把方程变形为a=-cos2x+sinx。
设f(x)=-cos2x+sinx(x∈(0,])。显然当且仅当a属于f(x)的值域时,a=f(x)有解。
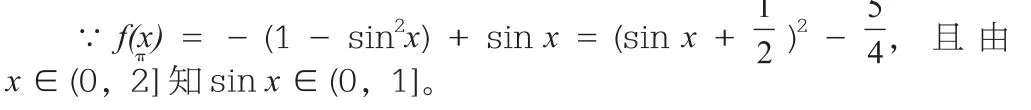
易求得f(x)的值域为(-1,1]。
解法二:令t=sinx,由x∈(0,],可得t∈(0,1]。将方程变为t2+t-1-a=0。
依题意,该方程在(0,1]上有解。设f(t)=t2+t-1-a。
其图象是开口向上的抛物线,对称轴t=-。

【评注】研究此类含参数的三角、指数、对数等复杂方程解的问题,通常有两种处理思路:一是分离参数构建函数,将方程有解转化为求函数的值域;二是换元,将复杂方程问题转化为熟悉的二次方程,进而利用二次方程解的分布情况构建不等式或构造函数加以解决。
二、 函数与方程思想在求最值或参数范围中的应用
【分析】参数a隐含在一个复杂的复合函数的表达式中,欲直接建立关于a的不等式(组)非常困难,故应转换思维角度,设法从原式中把a分离出来,重新认识a与其他变元(x)的依存关系,利用新的函数关系,常可使原问题“柳暗花明”。

三、函数与方程思想在数列问题中的应用
例3 设等差数列{an}的前n项的和为Sn,已知a3=12,S12>0,S13<0 。
①求公差d的取值范围; ②指出S1、S2、…、S12中哪一个值最大,并说明理由。
【分析】: ①问利用公式an与Sn建立不等式,容易求解d的范围;②问利用Sn是n的二次函数,将Sn中哪一个值最大,变成求二次函数中n为何值时Sn取最大值的函数最值问题。

【评注】数列的通项公式及前n项和公式实质上是定义在自然数集上的函数,因此可利用函数思想来分析或用函数方法来解决数列问题。也可以利用方程的思想,设出未知的量,建立等式关系即方程,将问题进行算式化,从而简洁明快。由此可见,利用函数与方程的思想来解决问题,要求灵活运用、巧妙结合,发展了学生思维品质的深刻性、独创性。
总之,综观高中数学,函数的图象及性质在解题中的应用非常广泛,而函数与方程思想是高中数学最重要也是最常用的思想方法之一,在解题中数学老师要做好函数与方程关系的揭示与转化,启发学生深刻认识数学问题的实质——数学知识的精髓,才能将知识转化为能力,才能提高学生灵活运用函数与方程思想解决问题的能力。

