一种基于最大基因组比对法的地理要素匹配相似度算法
高昭良
(福州市勘测院,福建 福州 350003)
一种基于最大基因组比对法的地理要素匹配相似度算法
高昭良*
(福州市勘测院,福建 福州 350003)
地理要素同名匹配是地理空间信息数据库实现要素级更新维护的基础,它对于提高地理空间信息现势性与应用水平具有重要的理论和实践意义。本文针对目前空间数据库变化特征进行了深入分析,并在此基础上,针对空间数据库快速更新需求,从几何视角提出了一种基于最大基因组比对法的地理要素匹配相似度算法,在空间信息数据库更新过程中验证了该匹配算法的可行性。
最大基因组比对法;要素匹配;空间数据库更新
1 引 言
随着基础数据库建设的不断完成,空间数据库的维护和更新逐步成为国际GIS学术界和应用部门的前沿研究与应用课题。由于目前常用的批量更新方式采用简单区域替代方法,严重损害了空间数据库变化的真实性,应用上造成所有的非空间信息全部失去空间关联。因此更新过程中如何快速识别同名空间要素(即:地理要素匹配技术),进行要素级的增量更新变化检测方法已成为GIS空间数据更新研究领域的热点问题。地理要素匹配其本质是通过分析两个数据集(新旧版本)中空间目标的差异与相似性,检测出不同数据集中表达现实世界同一地理要素的空间目标,目的是确定不同时期、不同尺度的同名地物是否发生变化,然后在不同数据之间传播变化以达到数据更新的目标[1]。就明确定义的点、线、面要素而言,国内外学者进行了深入的探讨与研究,提出了许多方法[2~10],这些方法在使用对象、技术细节等方面侧重点各不相同。现有匹配算法假设这些不同数据源中的同名地物具有强空间相似度,即空间相似度越好越能够得到肯定的匹配结果[11~14]。但总体从选取的匹配指标来说可以归纳为三类[15~17]:第一类是几何匹配的检测方法,通过分析不同类别数据中地物目标的几何空间特性,如形状、位置、方向、长度、大小等,计算其几何相似度,从而建立同名地物的对应关系。第二类是语义匹配的检测方法,即通过分析不同地物的属性信息,利用语义关联来实现匹配。第三类是拓扑匹配的检测方法,通过分析数据中地物目标的拓扑以及其他地物的空间关系。在实际操作中单纯运用某一类检测方法往往得不到正确的匹配结果,而往往需要综合运用语义、几何、拓扑等信息对目标进行综合匹配。
由上述分析可知,空间数据库更新中同名要素匹配是一个非常复杂过程,需要对此进行长期的深入研究。本文内容作为同名要素匹配中的分支算法,认为在相邻两个新旧版本的数据集中,同名地物之间可能会有所差别,但仍具有较高的空间相似度,从而基于遗传算法,提出了一种最大基因组比对法计算新旧地物相似度,实现了对几何上存在较小差异的同名要素之间的匹配。该方法能在相邻两个新旧版本的数据集中检测出一组粗略的地理要素匹配集合,缩小了拓扑和语义匹配的对象范围,极大地减少了后续匹配阶段的计算量。
2 最大基因组比对算法
2.1 遗传算法
遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出。其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则[10]。对于一个求函数最大值的优化问题(求函数最小值也类同),一般可以描述为下列数学规划模型:
maxf(x)
(1)
x∈R
(2)
R⊂U
(3)
式中x为决策变量,式(1)为目标函数式,式(2)、式(3)为约束条件,U是基本空间,R是U的子集。满足约束条件的解X称为可行解,集合R表示所有满足约束条件的解所组成的集合,称为可行解集合。
遗传算法的基本运算过程如下:
(1)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。
(2)个体评价:计算群体P(t)中各个个体的适应度。
(3)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
(4)交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
(5)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。
群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
(6)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
本文主要思路是基于遗传算法,借鉴生物学理论,将地理要素轮廓线看作生物基因链,其变化看做是基因遗传和变异的结果。新旧版本对象相似与否,可通过新旧地物基因比对来决定,如果新旧地物基因组重叠度长度大于某一个阀值,可判定其相似,否则不相似。算法涉及复杂的多变量最优化求解问题,本文采用改进的实数编码遗传算法进行求解。
2.2 最大基因组比对算法模型
最大基因组比对算法模型在遗传算法的基础上构建,包含了遗传算法的基本步骤,即是一个“产生+检测”(generate-and-test)的迭代过程,基本过程为:创建初始种群;种群中个体适应度计算;评估适应度;根据适应度选择个体;被选择个体进行交叉繁殖;在繁殖的过程中引入变异机制;淘汰掉最差的个体;回到第二步,直至满足要求为止。

图1 基因比对算法流程
使用遗传算法求解新旧地物的基因匹配问题,主要解决好编码、适应度、交叉、变异算法等问题,其中编码问题是遗传算法中至关重要的一步,直接影响后面适应度计算的复杂度,算法流程如图1所示。
在本文中,新地物集(即参考数据)表示为A={A1,A2,A3,…Am},旧地物集(即匹配数据)表示为B={B1,B2,B3,…Bn},其中Ai和Bj分别为参考数据集和匹配数据集中地物。
2.3 轮廓线标准化与编码

标准化后的地物表示为新版本地物a={a1,a2,a3,…am},其中ai为等距点;旧版本地物b={b1,b2,b3,…bm},其中bj为等距点。
编码是遗传算法中至关重要的一步,本文以地物要素的空间特征为表现型,并将表现型转化为基因型,即把求解空间中的参数转化成遗传空间中的染色体或者个体。针对新旧地物比对问题,本文采用长度为32位的二进制字符串表示新旧地物匹配的基点序号,即前面16位表示新地物的坐标序号,后16位表示旧地物的坐标序号。例如,假设两个地物都以1号点为基点开始匹配,其基因型就是:
0000,0000,0000,0001,
0000,0000,0000,0001。
2.4 适应度计算
考核一个基因型对当前环境的适应度,在本文中即考核地物相似程度,相似度越高的地物更有可能存活遗传下去,用适应函数f(x)表述,构建最大基因组评价模型。如图2所示,①为标准化后旧地物a={a1,a2,a3,…am},②为标准化后新地物b={b1,b2,b3,…bm},计算方法如下:
(1)对新地物进行旋转平移操作(二项式变换),使新旧地物基点前后3点~5点相互对齐,如图2(a)中a8、a9、a10点与图2(b)中b9、b10、b11号点对齐,旧地物基点为a9,新地物的基点为b10,平移旋转参数用最小二乘法求得。对其后效果如图2(c);

图2 最大基因组评价模型
(2)为保障算法鲁棒性,用双倍点位误差为缓冲距离,对旧地物轮廓线a作缓冲计算,如图2(c)窄条型多边形;从基点a9开始先向前逐点计算新地物点是否落入缓冲区内,直至不满足为止;然后向后逐点比对,直至不满足为止;落入总点数,即为单向适应度;
(3)设M,N为旧地物a={a1,a2,a3,…am}中标准化后的特征点数,n为新地物b={b1,b2,b3,…bm}中与a重合的特征点数,则单向适应度函数可表示为:
(4)对新地物轮廓线b作缓冲计算,用旧地物a进行叠加分析,可求得反向适应度。
(5)取两个单向适应度和反向适应度平均值作为总的适应度。
2.5 选择与交叉算子
选择算子采用赌轮的方式进行淘汰选择。先按照每个地物的适应度大小创建一个赌轮,设拥有不同基因的地物的适应度为f(xi),则选择概率可表示为:
当赌轮转动起来,总以较大概率选择适应度高的地物,即地物相似度高的地物。本文对赌轮选取4次,每次产生一个0~1的随机小数,然后判断该随机数落在哪个选择概率区间内就选取相对应的地物。这个过程中,选取概率P高的个体将可能被多次选择,而概率低的就则被淘汰。
两个父代地物在交叉后繁殖出了下一代的同样数量的地物。本算法采用黄金分割法进行交叉运算,即在黄金分割点0.618处进行交叉。设个体1新旧地物的比对基点分别是p11,p12;设个体2新旧地物的比对基点分别是p21,p22;交叉产生两个新的个体的比对基点p31,p32;p41,p42;交叉计算公式如下:
p31=p11*0.618+p21*0.382;
p32=p12*0.618+p22*0.382;
p41=p11*0.382+p21*0.618;
p42=p12*0.382+p22*0.618;
2.6 变异、淘汰与终止条件
变异概率太小,则可能陷入局部最优。变异概率太大,可能变成纯粹的随机算法,收敛速度太慢。经过本文提出的算法进行反复实验,取变异概率为0.01,效果较好。对种群中适应度最差的几个个体进行淘汰,但最新交叉繁殖和变异得到新种群不包括在此例。
本算法设置两类终止条件:一类是种群中最大适应度大于地物基因长度的90%,max(f(x))≥90%;
二类条件是迭代代数超过100代,最大适应度没有发生变化。以上两种类型视为已得到算法的稳定解。
3 实验与分析
为证实本文提出的匹配算法的有效性和适应性,选取福州市鼓楼区范围内约 2 km2的地形图及城市管理部件数据进行更新实验,分别采用Fourier描述子和本文提出的最大基因比对法进行相似度计算,实验结果选取了9组典型的匹配实例,计算结果如表1所示:
典型图形计算结果一览表 表1
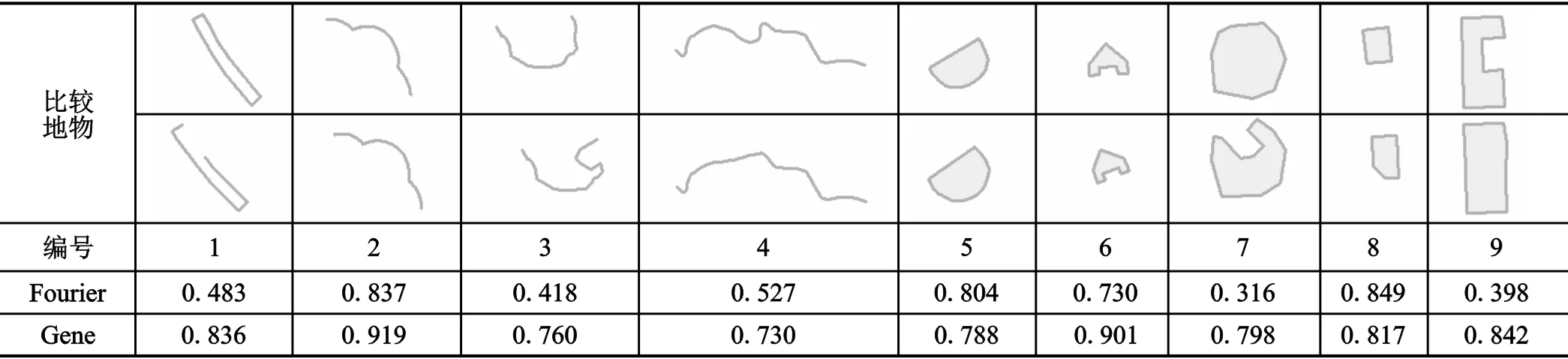
结果分析:2、5、8组图形Fourier法和Gene法结果相差不大,可以看出这几组图形的形状确实变化不大;1、3、6、7、9组计算结果差别很大,从图形上看,这几组地物出现了小部分变化,但仍具有较高的相似性,而在这几组结果数据中,Gene比对法均能计算出比Fourier更高的相似度。
结果表明:本文算法比传统相似度算法对局部较小变化有更强的容忍度,更适合空间数据库更新过程中的要素匹配,不仅可一次性计算出新旧地物的匹配度,而且具有较好的平移旋转不变性、和起点无关性。通俗地说,相似度结果计算过程有如我们打靶,我们首先寻找视野范围较大的靶标,然后调整准心寻找靶心。
4 结论与展望
本文空间数据库快速更新中地理要素匹配问题进行深入研究,采用空间信息科学与模糊数学相结合的分析方法,提出基于最大基因组比对模型的地物相似度计算方法,有效解决图形相似度匹配算法中存在的不足,并通过与Fourier算法在多组地物要素实例进行了实验和比较,证实该算法在同名地物检测过程中对小范围局部变化有较高的容忍度,适用于空间数据库更新过程中的要素匹配。地物要素匹配是空间数据库维护和更新的关键技术和研究基础,基于几何的地物相似度计算是其最重要的匹配方面之一,然而匹配精度的提高也需要语义、拓扑关系等指标的参与,因此综合多指标,采取不同匹配策略的地物要素匹配算法成为今后发展方向。
[1] Saalfeld,A. Conflation Automated map compilation[J]. International Journal of Geographical Information System,1988,2(3):217~228.
[2] Eliyah Safra,Yaron Kanza,etc. Efficient integration of road maps[C]. Proceedings of the 14th annual ACM international symposium on Advances in geographic information systems,New York,USA,2006.
[3] Sébastien Mustière. Thomas Devogele. Matching Networks with Different Levels of Detail[J]. Geoinformatica,2008,2(12):435~453.
[4] 陈玉敏,龚健雅,史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报,2007,36(1):84~90.
[5] 赵东保,盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报,2010,39(4):416~421.
[6] 胡云岗,赵仁亮,李志林等. 地图数据缩编更新中道路数据匹配方法[J]. 武汉大学学报·信息科学版,2010,35(4):451~456.
[7] Maythm Al-Bakri,David Fairbairn. Assessing Similarity Matching for Possible Integration of Feature Classifications of Geospatial Data from Official and Informal Sources[J]. International Journal of Geographical Information Science,2012,26(8):1~20.
[8] 田文文,朱欣焰,呙维. 一种VGI矢量数据增量变化发现的多层次蔓延匹配算法[J]. 武汉大学学报·信息科学版,2014,39(8):963~967.
[9] 徐枫,邓敏,赵彬彬等. 空间目标匹配方法的应用分析[J]. 地球信息科学学报,2009,11(5):657~663.
[10] 王涛,刘文印,孙家广等. 傅立叶描述子识别物体的形状[J]. 计算机研究与发展,2002,13(12):1715~1718.
[11] 唐炉亮,李清泉,杨必胜. 空间数据网络多分辨率传输的几何图形相似性度量[J]. 测绘学报,2009,38(4):336~340.
[12] 赵宇,陈雁秋. 曲线描述的一种方法:夹角链码[J]. 软件学报,2004,15(2):300~307.
[13] Kieler B,Sester M,Wang H,etal. Semantic Data Integration:Data of Similar and Different Scales[J]. Photogrammetrie Femerkundung Geoinformation,2007,3(6):447~457.
[14] 丁虹. 空间相似性理论与计算模型的研究[D]. 武汉:武汉大学,2004,13~34.
[15] 童小华,邓愫愫,史文中. 基于概率的地图实体匹配方法[J]. 测绘学报,2007,36(2):210~217.
[16] 张桥平,李德仁,龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报,2004,8(2):107~112.
[17] 赵彬彬. 多尺度矢量地图空间目标匹配方法及其应用研究[D]. 长沙:中南大学,2011.
A Method of Geographical Feature Matching Based on the Largest Genome Comparison
Gao Zhaoliang1,2
(Fuzhou Investigation and Mapping Institute,Fuzhou 350003,China)
Geographical feature matching technology is the technical basement of update maintenance of geographic spatial database. It has important theoretical and practical significance to improve the level of geospatial information application and timeliness. This paper makes a detailed analysis for changes of the spatial database,points out the shortage of the existing matching technology,based on this,a matching algorithm based on the largest genome comparison method is introduced from the perspective of geometry for oriented spatial database rapid updating. And the feasibility of the method is validated.
the largest genome comparison method;feature matching;spatial database updating
1672-8262(2016)06-10-04
P208,O235
A
2016—05—31
高昭良(1972—),男,博士,高级工程师,主要从事测绘、地理信息生产研究工作。
国家863计划资助项目(2013AA01A608)

