考虑多时钟周期瞬态脉冲叠加的锁存窗屏蔽模型
闫爱斌,梁华国,黄正峰,蒋翠云,易茂祥
(1.合肥工业大学计算机与信息学院,安徽合肥 230009;2.安徽大学计算机科学与技术学院,安徽合肥 230601;3.合肥工业大学电子科学与应用物理学院,安徽合肥 230009;4.合肥工业大学数学学院,安徽合肥 230009)
考虑多时钟周期瞬态脉冲叠加的锁存窗屏蔽模型
闫爱斌1,2,梁华国3,黄正峰3,蒋翠云4,易茂祥3
(1.合肥工业大学计算机与信息学院,安徽合肥 230009;2.安徽大学计算机科学与技术学院,安徽合肥 230601;3.合肥工业大学电子科学与应用物理学院,安徽合肥 230009;4.合肥工业大学数学学院,安徽合肥 230009)
集成电路工艺水平的提升,使得由单粒子瞬态脉冲造成的芯片失效越发不容忽视.为了准确计算单粒子瞬态脉冲对锁存器造成的失效率,提出一种考虑多时钟周期瞬态脉冲叠加的锁存窗屏蔽模型.使用提出的考虑扇出重汇聚的敏化路径逼近搜索算法查找门节点到达锁存器的敏化路径,并记录路径延迟;在扇出重汇聚路径上,使用提出的脉冲叠加计算方法对脉冲进行叠加;对传播到达锁存器的脉冲使用提出的锁存窗屏蔽模型进行失效率的计算.文中的锁存窗屏蔽模型可以准确计算扇出重汇聚导致的脉冲叠加,并对多时钟周期情形具有很好的适用性.针对ISCAS’85基准电路的软错误率评估结果表明,与不考虑多时钟周期瞬态脉冲叠加的方法相比,文中方法使用不到2倍的时间开销,平均提高7.5%的软错误率评估准确度.
锁存窗屏蔽;脉冲叠加;多时钟周期;扇出重汇聚
1 引言
工艺尺寸的降低,使得空间辐射效应引起的软错误成为纳米集成电路相当主要的不可靠因素来源之一[1,2].软错误是由集成电路瞬态故障引起的暂时性错误,而集成电路发生瞬态故障的主要原因是空间辐射环境中各种能量的中子或芯片封装材料中铀和钍掺杂发生放射性衰减发出α粒子的撞击[2].随着工艺水平的提高,组合逻辑门节点电容与工作电压呈现减小趋势,致使门节点临界电荷降低,导致低能量粒子的撞击便可产生足够的沉积电荷从而发生软错误,加重了组合逻辑对软错误的敏感性,并且组合逻辑相对于存储单元发生软错误的比重越发突出[3],由此引发的集成电路容错设计面临巨大挑战.
粒子撞击组合逻辑门单元敏感区,在门的输出端产生可观测的电压扰动,表现为单粒子瞬态(Single Event Transient,SET)脉冲[2].产生的SET脉冲若能够传播到存储单元,则可能被捕获,从而发生软错误.在早期深亚微米工艺水平下,组合逻辑对SET脉冲的屏蔽效应相对显著,主要体现在[2,4]:(1)逻辑屏蔽,即产生SET脉冲的引脚,由于受到逻辑门控制值的影响,不存在到达存储单元或主输出的数据通路,脉冲被屏蔽;(2)电气屏蔽,即在数据通路上传播的SET脉冲,由于受到逻辑门的削弱作用,其宽度/幅值被弱化;(3)锁存窗屏蔽,即到达存储单元的SET脉冲,由于未落在有效的锁存窗口之内,或其有效宽度和幅值较小,不满足存储单元采样时间,脉冲被屏蔽.有效幅值为器件逻辑值翻转阈值,有效宽度为正/负脉冲上升/下降沿到达有效幅值的时间点与下降/上升沿到达有效幅值的时间点之差.下文提及的脉冲宽度如不特殊说明,均指有效宽度.易知,SET脉冲能否被捕获,最终取决于锁存窗屏蔽效应.
失效率是指工作到某一时刻尚未失效的器件或系统,在该时刻后,单位时间内发生失效的概率.由空间辐射效应引起的失效率,其评估方法大体上分为两类:辐射试验和软件仿真.由于辐射试验方法需要流片,成本高、试验周期长,因而软件仿真的方法被业界广泛采用.软件仿真方法的准确性高度依赖于故障模型和故障传播模型[5],而锁存窗屏蔽模型恰恰是故障模型和故障传播模型的核心,亦是评估组合电路失效率的关键步骤,因而锁存窗屏蔽模型的精确与否,将对失效率的计算结果造成不同程度的偏差.
在纳米工艺下,由于时钟周期和路径延迟的减小,扇出重汇聚问题变得越发不容忽视,并且对于单粒子事件,扇出重汇聚是导致SET脉冲发生叠加的一个重要因素[6].粒子撞击组合逻辑门单元G产生的SET脉冲,沿着以G的各个扇出门为起始点的多条路径进行传播,并且最终汇聚到同一个门单元,脉冲可能会发生叠加,这种现象称为SET脉冲的扇出重汇聚.以NOR2为例,图1给出扇出重汇聚导致SET脉冲叠加的情形.如图1(a)所示,粒子撞击G1产生的SET脉冲分别沿路径1和路径2传播到达汇聚点G6,发生叠加,形成一个新的SET脉冲.叠加结果如图1(b)所示,左半部分为最坏情况,即门G2、G3延迟的和Tdly与脉宽相当,叠加后脉宽最大.右半部分为是最好情况,即Tdly很小或当G2、G3逻辑门不存在时,叠加后脉宽最小,且由两个脉冲变为一个脉冲.若不考虑脉冲叠加,则认为传播到达G6的两个脉冲相互独立,计算失效率时分别被采样/屏蔽,相当于被计算两次,这显然与实际情况不符,对失效率的计算结果造成了偏差.

Massengill L W等人对90-nm体硅工艺CMOS器件产生的SET脉冲宽度进行了实测,在室温下的最大脉宽为1500ps[7].这意味着,当时钟频率超过667Mhz,此类脉冲将对多个时钟周期的采样造成影响.与此同时,Schwank J R等人也指出脉宽会大于一个时钟周期的情形[8].进一步地,由图1(b)可知,传播到A、B输入端的脉冲宽度已超过一个时钟周期的宽度Tclk,叠加后的脉冲宽度可能会比Tclk大得多,因此需要考虑多时钟周期的情形.SET脉冲的产生可由双指数电流源进行模拟[9].对宽脉冲考虑多时钟周期的情形相当于对故障点在多个时钟周期持续施加故障模拟电流源;仅考虑单时钟周期的情形相当于对故障点只在发生故障的单个时钟周期之内施加故障模拟电流源,并在下一个时钟周期到来时撤销施加故障模拟电流源.
目前国际上较为典型的几种失效率评估方法都使用了不同的锁存窗屏蔽模型[10~14],这些模型至少存在如下缺陷:
(1) 存在明显的建模错误[10,11,13,14];
(2)未考虑脉冲叠加的情形,认为汇聚到门节点的各个脉冲是相互独立的[10,12~14];
(3)未考虑多时钟周期的情形,认为一个脉冲最多只被锁存一次[10~13];
(4) 考虑了脉冲叠加的情形,但没有考虑多时钟周期的情形[11];
(5)考虑了多时钟周期的情形,但模型不准确,论证不充分[14].
本文提出的锁存窗屏蔽模型考虑了多时钟周期脉冲叠加的情形,提高了锁存窗屏蔽效应评估的准确度.首先使用提出的敏化路径逼近搜索算法可以准确计算门节点到达锁存器的敏化路径及路径延迟;其次在扇出重汇聚路径上,使用提出的脉冲叠加计算方法可以对叠加的脉冲进行准确的脉宽计算;最后对传播到达锁存器的脉冲使用提出的锁存窗屏蔽模型可以准确进行失效率的评估.分析验证和针对ISCAS’85基准电路的实验结果表明,提出的锁存窗屏蔽模型对于纳米工艺下组合电路的失效率和软错误率的评估,适用性更好,计算结果更精确,能够为组合电路脆弱节点的筛选和选择性加固提供参考,具有重要的研究意义和应用价值.
2 现有的锁存窗屏蔽模型
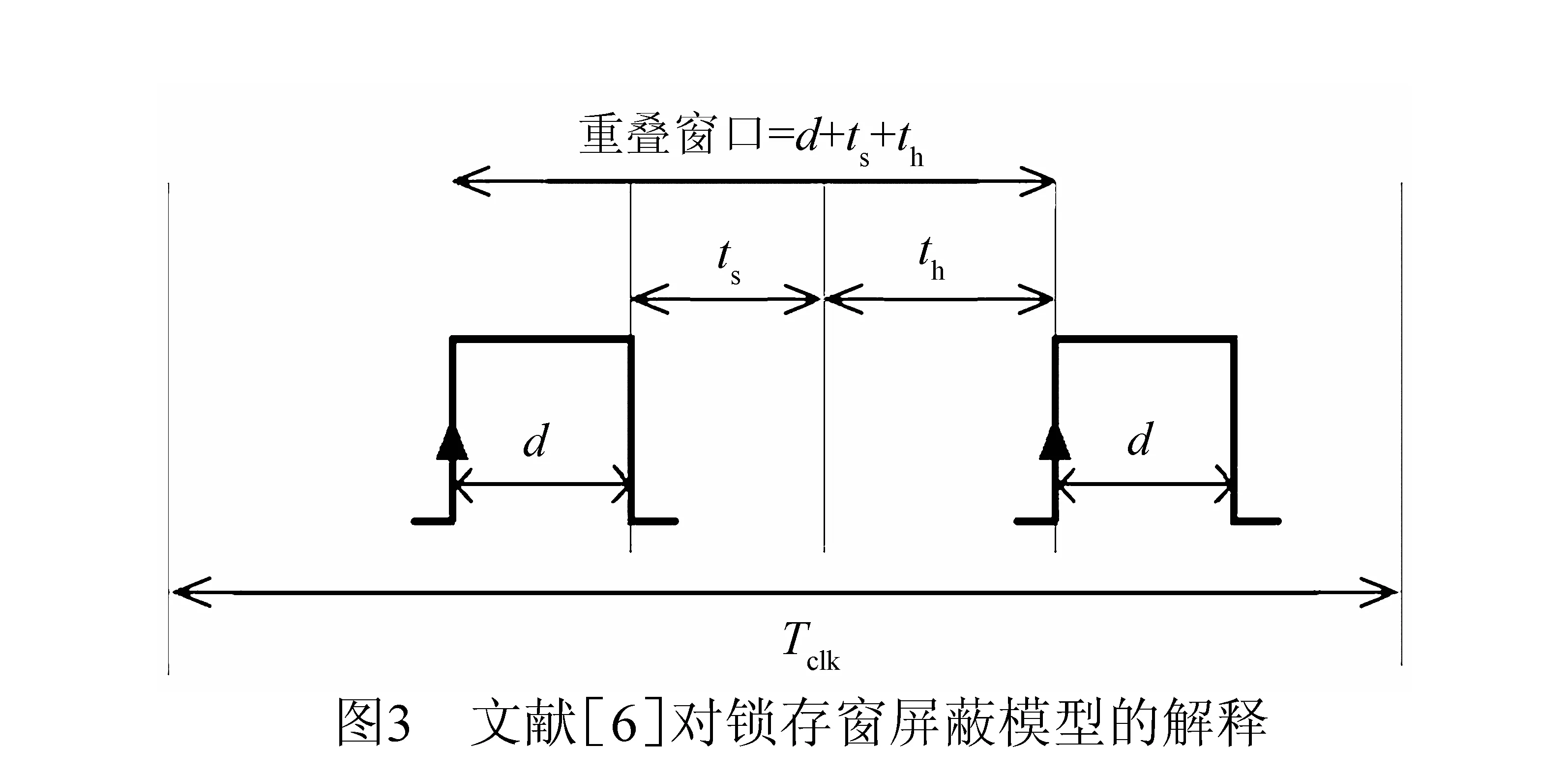
以高电平采样的锁存器为例,图2给出了SET脉冲被锁存和被屏蔽的情形.脉冲覆盖锁存窗口,且其有效宽度d大于锁存窗口宽度Tsh,则被锁存.此外的情形,脉冲均被屏蔽.Tsh由锁存器建立时间ts和保持时间th决定.ts是时钟翻转之前输入的数据必须保持稳定的时间,th是时钟翻转之后输入数据必须保持稳定的时间.一个数据若要在上升沿被锁存,那么这个数据就要在时钟上升沿的建立时间和保持时间内保持稳定.
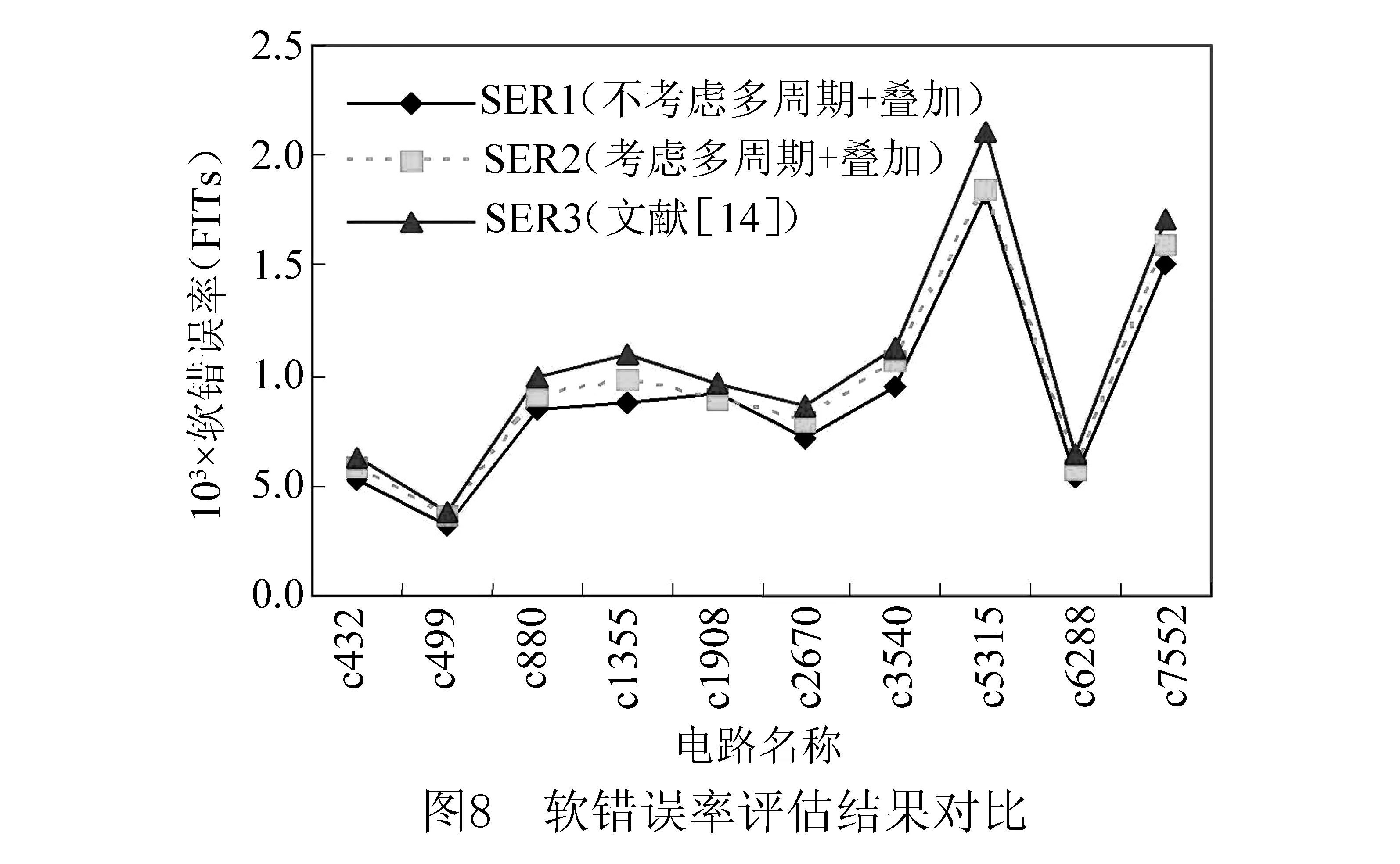
美国东北大学Tahoori M B等人提出一种粗略的锁存窗屏蔽模型[10],具体如式(1)所示.其中d为脉冲宽度,Platching为SET脉冲被锁存的概率,即锁存器失效概率.图3给出了对该模型的解释,认为失效概率是d与ts和th的重叠量相对整个时钟周期Tclk所占的比例.但是,当d (1) 美国卡内基梅隆大学Marculescu D等人提出一种改进的锁存窗屏蔽模型[11],具体如式(2)所示.其中dk为沿着不同敏化路径到达锁存器的SET脉冲宽度,dinit为SET脉冲初始宽度.认为到达锁存器的各个脉冲是相互独立的,失效概率的计算是机械式的累加,并且也未对多时钟周期的情形进行分析验证.此外,在纳米工艺下,时钟频率的提高导致Tclk降低,dinit可能会与Tclk相当,甚至大于Tclk,导致模型计算结果为无穷大或为负,进一步说明该模型是不合理的. (2) 美国密歇根大学Sylvester D M等人提出一种较为合理的锁存窗屏蔽模型[12],具体如式(3)所示.但是,由于未考虑到脉冲发生叠加的情形,并且也未对多时钟周期的情形进行分析验证,因此该模型仍然存在缺陷. (3) 美国奥本大学的Agrawal V D等人对式(3)模型进行改进[13],具体如式(4)所示.对多周期情形的分析初见端倪,认为过大的SET脉冲必然会造成一次失效.加入Platching=1的条件分支,看似合理.然而实际上会存在该种情形:过大的SET脉冲会造成多次失效!如图4所示,脉冲d1会被多次锁存.如果正确的数据始终是低电平,则d1会造成锁存器发生两次失效,而式(4)的计算结果最大值仅为1.此外,式(4)还存在与式(3)相同的缺陷. (4) 台湾国立交通大学Wen H P等人考虑到脉冲在多个时钟周期被采样的情形,对式(4)模型进行改进[14].将失效概率表述为失效率,失效率一般以λ表示,取值可以大于1.他们将式(4)改写为式(5)的形式,并被提出的式(7)模型进行调用.其中Nerr为脉宽d相对于Tclk的倍数,取下确界整数值.d′为去除d中Tclk整数倍宽度的脉宽余量.认为d为Tclk的N倍,就必然会产生N次失效.这显然是不合理的.如图4所示,d2为Tclk的2倍,但实际上d2只被锁存一次.同样,式(7)还存在与式(3)相同的缺陷. (5) w=ts+th (6) λ(d,w)=Nerr+λ(d′,w) (7) (8) d′=d-Nerr·Tclk (9) 综上所述,现有的锁存窗屏蔽模型要么未考虑脉冲叠加,要么未考虑多周期的情形,要么存在明显的错误,因而不够精确.使用该类锁存窗屏蔽模型计算电路失效率,并评估电路的脆弱节点,将对集成电路的选择性抗辐射加固造成误导,从而影响集成电路芯片在航空、航天等高可靠需求领域的应用. 本节首先给出扇出重汇聚导致的多时钟周期瞬态脉冲叠加的计算方法,然后给出考虑脉冲叠加的锁存窗屏蔽模型,最后对该模型在单时钟周期情形以及多时钟情形下的适用性进行理论分析和验证. 3.1 多时钟周期瞬态脉冲的叠加 图1给出了G1产生的SET脉冲分别沿路径1和路径2传播到达汇聚点G6,发生叠加并形成一个新SET脉冲的情形.与此同时,图5给出了G1、G5、G4、G6输出端的SET脉冲波形.G1产生一个0-1-0型SET脉冲,由于路径2延迟较小,G5输出端的波形被事先观测到;由于路径1延迟较大,G4输出端的波形经过一个延迟差后被观测到;由于脉冲汇聚到G6并发生叠加,由此产生一个新的SET脉冲(1-0-1型,宽度为dG5+dG4-dovlp).G5、G4输出端的脉冲存在一个重叠量dovlp,对于图5的情形,dovlp越大,G6输出端的脉冲宽度越小.此时若认为传播到G6的两个脉冲是独立的(总宽度为dG5+dG4),产生的失效率评估误差最大,并且被高估. 不失一般性,现将汇聚到NOR2的脉冲所有叠加情形加以讨论,具体如图6所示.A、B、Out分别为NOR2的两个输入引脚和输出引脚.传播到A、B端的脉冲,dovlp为其重叠部分,dApure和dBpure分别为去除重叠部分的自身部分.考虑叠加的情形共有四种,Out端给出了叠加后的情形.忽略脉冲叠加的情形共有两种,认为脉冲是独立的,则当NOR2的一个输入引脚为恒定的非控制值时,穿过另一个引脚的脉冲被原样输出. 当考虑脉冲叠加,Out端脉冲宽度dconsider可以表示为: (10) 当不考虑脉冲叠加,Out端脉冲宽度dignore可以表示为: dignore=P(A=0)×dB+P(B=0)×dA (11) 注意到, (2) (13) (14) 因此有: dignore-dconsider=(1-2×P(A=1,B=1))dovlp (5) P(A=1,B=1)概率值取决于电路拓扑结构和输入激励,当P(A=1,B=1)<0.5时,忽略脉冲叠加将导致失效率被高估;当P(A=1,B=1) > 0.5时,忽略脉冲叠加将导致失效率被低估.不失一般性,假定P(A=1)=P(B=1)=0.5,则P(A=1,B=1)=0.25.因此,忽略脉冲叠加将导致失效率被高估0.5dovlp.依据上述方法,对于其他类型的逻辑门亦可得出类似结论,在此从略. 对于扇出重汇聚导致脉冲叠加的情形,准确的敏化路径搜索是需要优先解决的问题.顾名思义,敏化路径是被敏化的路径,它要求处于敏化路径上的逻辑门单元的非敏化引脚需为非控制值,否则会发生逻辑屏蔽导致路径被切断.图1给出G1到G6的两条敏化路径,当IN1和IN4为控制值0时,路径1和路径2均将被切断.图5给出脉冲延迟差和重叠量,在搜索敏化路径时通过计算路径1和路径2路径时延可得.下面给出考虑扇出重汇聚的敏化路径逼近搜索算法(算法1.FindSensPathsByInjFaults). 算法1 FindSensPathsByInjFaults //输入:初始敏化路径与延迟链表lstSensPathAndDelayInitial,故障门gFtSrc,目标门gDest. // 输出:整体敏化路径与延迟链表lstSensPathAndDelayTotally. 对故障门的扇出进行广度优先搜索(breadth first search, BFS)并记录故障敏化扇出门; // 故障敏化扇出门数据结构为list〈gate*〉 lstFoSensGates FOR lstFoSensGate ← lstFoSensGates.begin() to lstFoSensGates.end() DO 建立当前敏化路径与延迟链表lstSensPathAndDelayCurrent; 将lstSensPathAndDelayInitial数据记入lstSensPathAndDelayCurrent; 查找敏化引脚对应延迟并将lstFoSensGate与延迟记入lstSensPathAndDelayCurrent; IF(lstFoSensGate逼近到达gDest) 将链表lstSensPathAndDelayCurrent记入链表lstSensPathAndDelayTotally; ELSE gFtSrc=lstFoSensGate; FindSensPathsByInjFaults(lstSensPathAndDelayCurrent,gFtSrc,gDest); ENDIF END 给定电路拓扑结构,输入激励决定敏化路径序列.通过电路门级仿真,可得所有逻辑门各个引脚信号.算法通过对门(如,G1)的输出信号进行翻转以模拟故障注入并进行故障传播,可得待锁存值发生翻转的锁存器LAupset.算法将LAupset的元素作为目标门,将故障注入门作为故障门,将发生翻转的锁存器与零延迟一并作为初始敏化路径与延迟链表的元素.进行如上算法所列举的操作,可得故障门到达锁存器的全部敏化路径.通过恢复对故障门输出信号的翻转并对其扇出锥进行二次门级仿真,可以清除故障注入. 算法首先对故障门的扇出进行BFS搜索并记录故障敏化扇出门,而后分别将故障敏化扇出门及其敏化引脚延迟记录到当前敏化路径与延迟链表中,故障敏化扇出门若已逼近到达目标门,则需将当前敏化路径与延迟链表记录到整体敏化路径与延迟链表中,否则便将故障扇出门设定为当前故障门并递归调用本算法,最终只将能够到达目标门的链表记录到整体敏化路径与延迟链表中而得解. 综上所述,通过精确搜索敏化路径,并记录发生扇出重汇聚的子路径及其延迟,给定初始SET脉冲,便可准确计算dconsider.图6给出时钟信号CLK的变化情况,以上讨论的SET脉冲叠加对多时钟周期的情形具有很好的适用性. 3.2 提出的锁存窗屏蔽模型 (16) 下面对其在单周期情形下的正确性进行验证. 假定脉冲汇聚到任意逻辑门G发生叠加后宽度为D0,经历时间tprop最终到达锁存器LA,宽度变为D.图7给出脉冲在单个时钟周期内传播的情形,tprop为D0传播到达LA的传播时延,VS,G为G的翻转阈值.有如下结论: (17) (18) 若D被锁存,需满足以下条件: (19) (20) D>Tsh (21) 因此有: t1∈(Tclk+th-tprop-D,Tclk-ts-tprop) (22) 此外,若D被锁存,还需要满足一个条件,即要么A′>VS,LA(当非故障采样值为0),要么A′ 由于t1在一个时钟周期T∈[0,Tclk]之内随机出现,假定t1在区间T内服从均匀分布,则发生式(22)事件的概率为: P(t1∈(Tclk+th-tprop-D,Tclk-ts-tprop)) (23) 显然,其值为(D-Tsh)/Tclk。 综上,当D≤Tsh,D被锁存的概率为0;当D>Tsh,D被锁存的概率为(D-Tsh)/Tclk,得证. 下面对其在多周期情形下的正确性进行验证. (1) 当D≤Tsh时,失效次数必然为0,λ=0; (2) 当D∈(Tsh,Tclk+Tsh]时,失效次数为0或1.如图3所示,脉冲d3宽度恰好达到该条件的上界,此时无论d3如何移动,必然覆盖一个锁存窗口,造成一次失效.如同单时钟周期情形下正确性的验证,失效1次的概率为P1=(D-Tsh)/Tclk,则失效0次的概率为P0=1-P1,有λ=0×P0+1×P1=P1=(D-Tsh)/Tclk. (3) 当D∈(Tclk+Tsh,2Tclk+Tsh]时,失效次数为1或2.一旦脉冲宽度达到该条件上界,必然覆盖两个锁存窗口,造成两次失效.如同单时钟周期情形下正确性的验证,失效2次的概率为P2=(D-(Tclk+Tsh))/Tclk,则失效1次的概率为P1=1-P2,有λ=1×P1+2×P2=1+P2=(D-Tsh)/Tclk. (4) 按照上面的方法,以此类推.因此有5). (5)当D∈(N·Tclk+Tsh,(N+1)·Tclk+Tsh]时,失效次数为N或N+1,其中N=(D-Tsh)/Tclk,取下界整数值.一旦脉冲宽度达到该条件的上界,必然覆盖N+1个锁存窗口,造成N+1次失效.如同单时钟周期情形下正确性的验证,失效N+1次的概率为PN+1=(D-(N·Tclk+Tsh))/Tclk,因此失效N次的概率为PN=1-PN+1,有λ=N×PN+(N+1)×PN+1=N+PN+1=(D-Tsh)/Tclk. 易知,以上讨论的(1)~(5)情形等价于: (24) 综上,当D≤Tsh,D造成的失效率为0,λ=0;当D>Tsh,D必然落在区间(N·Tclk+Tsh,(N+1)·Tclk+Tsh]之内,N为自然数,此时D造成的失效率均为(D-Tsh)/Tclk,λ=(D-Tsh)/Tclk,得证. 为进一步验证本文方法的正确性,使用45nm Nangate标准单元库,对ISCAS′85基准电路进行考虑多时钟周期瞬态脉冲叠加的软错误率(soft error rate,SER)计算,并与同类文献进行对比分析. 4.1 软错误率的计算 软错误率是器件或系统发生软错误的比率,式 (25)给出了软错误率的计算公式. SER=λckt×RPH×Reff×Ackt×3.6×1012 (25) 上式中λckt为电路整体失效率,RPH与Reff分别为辐射环境中的粒子通量与有效撞击率,参考文献[11,12]分别取值为56.5m-2s-1、2.2×10-5.Ackt为组合电路全部逻辑门单元面积总和. 对于特定标准门单元库,首先建立各个标准逻辑门单元特征参数表,将提取的各个门单元引脚电容与延迟、负载参数及面积信息存储到程序数据结构,然后通过算法2计算电路软错误率. 其中N为测试向量个数,S为敏化路径条数,W为脉冲注入个数,G为敏化路径上的门单元.算法首先读取输入参数并解析电路网表,然后随机生成若干组测试向量.针对每一组测试向量,进行如下操作:(1) 逻辑仿真,使用提出的敏化路径逼近搜索算法查找各个门单元到锁存器的敏化路径,识别扇出重汇聚子路径并标记扇出点与汇聚点;(2) 对处在敏化路径上的第一个门单元进行不同宽度的脉冲注入以模拟不同能量的粒子来袭,然后将脉冲在敏化路径上进行传播,并协同计算脉冲叠加与电气屏蔽效应.通过文献[12]提出的电气屏蔽模型评估电气屏蔽效应;(3) 使用提出的锁存窗屏蔽模型计算脉冲对锁存器造成的失效率并统计电路总体失效率.最后,取各个测试向量下的电路平均失效率,进而通过式(25)计算可得电路总体软错误率. 算法2 SERComputing //输入:电路网表、测试向量数目、工艺库参数. //输出:电路总体软错误率. 读取输入参数并解析电路网表; 使用随机向量生成器产生测试向量; FORi← 1 toNDO 电路逻辑仿真; 查找敏化路径并记录路径延迟; 识别扇出重汇聚子路径并标记扇出点与汇聚点; FORj← 1 toSDO FORw← 1 toWDO FORk← 1 toGDO 协同计算脉冲叠加与电气屏蔽效应; END 计算锁存窗屏蔽效应; 统计电路总体失效率; END END END 计算电路总体软错误率; 4.2 实验结果的比较 本文实验环境为Windows XP x86 SP3 OS、4GB内存、Intel Quad-Core i5处理器. 将时钟频率设定为2GHz,Tsh设定为30ps[15],随机产生1000组测试向量[16],使用如下双指数电流源[9]进行初始SET脉冲宽度生成. (26) 其中Q为电荷收集量,τα为电荷收集时间常数,τβ为电荷通道建立时间常数.45nm工艺下,τα和τβ分别取值为1.5×10-10、5×10-11s. 针对Q∈[0,300fc]中10的整数倍电荷量的粒子进行初始脉宽生成,使用第3节提出的多周期瞬态脉冲叠加方法对SET脉冲进行叠加并计算脉冲对电路造成的总体软错误率,计算结果如表1所示. 表1中SER1与时间1、SER2与时间2分别为不考虑和考虑多时钟周期瞬态脉冲叠加的软错误率计算结果与时间开销,SER3与时间3为文献[14]中仅考虑多时钟周期情形的软错误率计算结果与时间开销.由于同类文献甚少,因此本文主要与同类文献[14]进行比较.定义A方法软错误率评估结果SERA相对于B方法软错误率评估结果SERB的偏差SERdiff为: (27) 因此有表1数据diff21、diff32,含义分别为SER2相对SER1以及SER3相对SER2的软错误率偏差,从而有其均值7.5%与9.2%.这意味着:(1)与考虑多时钟周期瞬态脉冲叠加的软错误率计算结果相比,不考虑多时钟周期瞬态脉冲叠加的软错误率计算结果要被低估7.5%.分析其原因,虽然3.1节从统计学角度指出忽略脉 表1 软错误率计算结果与时间开销 数据指出考虑多时钟周期的情形会使软错误率计算结果更高[14].由此可见,相比于扇出重汇聚导致的脉冲叠加,多时钟周期情形导致的软错误率提升占据主导地位,因而综合考虑多时钟周期瞬态脉冲叠加的软错误率计算结果SER2要比SER1偏高.(2)文献[14]的软错误率计算结果SER3比本文SER2还要高9.2%.分析其原因,文献[14]认为脉宽是时钟周期的多少倍,就会至少造成多少次失效,软错误率显然被高估.此外,图8给出SER1、SER2、SER3的对比结果,它们具有一致的变化趋势,进一步说明本文方法是合理的. 关于时间开销,本文使用考虑扇出重汇聚的敏化路径逼近搜索算法,并进行脉冲叠加,因而引入较多的时间开销.由表1可知,SER2平均计算时间约为SER1平均计算时间的1.7倍,但是本文的软错误率计算准确度平均提高7.5%.此外,由于文献[14]使用高性能计算机评估软错误率,其时间开销较小.由于计算平台的不一致性,本文未与其进行时间开销的比较. 集成电路工艺水平的不断提升,导致锁存器越发容易受到单粒子瞬态脉冲的干扰而发生误采样.高性能集成电路工作频率的提高,路径延迟的降低,使得扇出重汇聚导致的SET脉冲叠加越发不容忽视.理论分析表明,扇出重汇聚导致叠加的SET脉冲可能更宽.同时,时钟周期的减小,进一步加重了叠加的脉冲在多个周期之内对锁存器的干扰.提出的锁存窗屏蔽模型,充分考虑扇出重汇聚导致的SET脉冲叠加,并对多时钟周期情形具有很好的适用性.本文方法与不考虑多时钟周期瞬态脉冲叠加的方法相比,使用不到2倍的时间开销,平均提高7.5%的软错误率评估准确度,能够为电路脆弱节点的筛选和选择性抗辐射加固提供参考. [1]Wu K C,Marculescu D.A low-cost,systematic methodology for soft error robustness of logic circuits [J].IEEE Transactions on Very Large Scale Integration Systems,2013,21(2):367-379. [2]Ferlet-Cavrois V,Massengill L W,Gouker P.Single event transients in digital CMOS—A review[J].IEEE Transactions on Nuclear Science,2013,60(3):1767-1790. [3]Black J D,Dodd P E,Warren K M.Physics of multiple-node charge collection and impacts on single-event characterization and soft error rate prediction[J].IEEE Transactions on Nuclear Science,2013,60(3):1836-1851. [4]Zhang M,Shanbhag N R.Soft-error-rate-analysis (SERA) methodology[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2006,25(10):2140-2155. [5]Chen L,Ebrahimi M,Tahoori M B.CEP:correlated error propagation for hierarchical soft error analysis[J].Journal of Electronic Testing,2013,29(2):143-158. [6]Liu B W,Chen S M,Liang B,et al.The effect of re-convergence on SER estimation in combinational circuits[J].IEEE Transactions on Nuclear Science,2009,56(6):3122-3129. [7]Gadlage M J,Ahlbin J R,Narasimham B,et al.Increased single-event transient pulsewidths in a 90-nm bulk CMOS technology operating at elevated temperatures[J].IEEE Transactions on Device and Materials Reliability,2010,10(1):157-163. [8]Dodd P E,Shaneyfelt M R,Felix J A,et al.Production and propagation of single-event transients in high-speed digital logic ICs[J].IEEE Transactions on Nuclear Science,2004,51(6):3278-3284. [9]Messenger G C.Collection of charge on junction nodes from ion tracks[J].IEEE Transactions on Nuclear Science,1982,29(6):2024-2031. [10]Asadi H,Tahoori M B.Soft error derating computation in sequential circuits[A].Proceedings of the IEEE/ACM International Conference on Computer-aided Design[C].Taiwan:IEEE,2006.497-501. [11]Miskov-Zivanov N,Marculescu D.Circuit reliability analysis using symbolic techniques[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2006,25(12):2638-2649. [12]Rao R R,Chopra K,Blaauw D T,et al.Computing the soft error rate of a combinational logic circuit using parameterized descriptors[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2007,26(3):468-479. [13]Wang F,Agrawal V D.Soft error rate determination for nanoscale sequential logic[A].Proceedings of the 11th IEEE International Symposium on Quality Electronic Design[C].Santa Clara:IEEE,2010.225-230. [14]Huang H M,Wen H P.Advanced soft-error-rate (SER) estimation with striking-time and multi-cycle effects[A].Proceedings of the 51st Annual Design Automation Conference on Design Automation Conference[C].San Francisco:IEEE,2014.11-16. [15]Salman E,Friedman E G.Reducing delay uncertainty in deeply scaled integrated circuits using interdependent timing constraints[A].Proceedings of the ACM/IEEE International Workshop on Timing Issues in the Specification and Synthesis of Digital Systems[C].New York:IEEE,2010.1-6. [16]Holcomb D,Li W C,Seshia S A.Design as you see FIT:System-level soft error analysis of sequential circuits[A].Proceedings of the Conference on Design,Automation and Test in Europep[C].Dresden:IEEE,2009.785-790. 闫爱斌 男,1983年生于吉林白城,2015年获得合肥工业大学计算机应用技术专业工学博士学位,现为安徽大学计算机科学与技术学院讲师.主持国家自然科学基金一项(编号为61604001),研究方向为纳米集成电路软错误率评估和星载系统芯片SoC的抗辐射加固. E-mail:abyan@mail.ustc.edu.cn 梁华国 男,1959年生于安徽合肥,2003年博士毕业于德国斯图加特大学,现为合肥工业大学电子科学与应用物理学院和计算机与信息学院教授、博士生导师.1998年至2003年,在德国斯图加特大学计算机科学系作访问学者,并获得德国斯图加特大学博士学位.先后主持或参加多项国际和国内的国家级研究与开发项目,包括德国国家自然科学基金(DFG)、国家自然科学基金面上项目和重点基金项目、国家教育部回国人员科研启动基金.出版德文专著一本,发表论文超过100篇.研究兴趣包括内建自测试、数字系统设计自动化、ATPG算法以及分布式控制系统等.E-mail:huagulg@hfut.edu.cn 黄正峰 男,1978年生于安徽无为,现为合肥工业大学电子科学与应用物理学院副教授、硕士生导师.研究兴趣主要包括星载系统芯片SoC的抗辐射加固、嵌入式系统的综合与测试、数字系统设计自动化等. E-mail:huangzhengfeng@139.com 易茂祥 男,1964年生于安徽广德县,2010年获得合肥工业大学计算机应用技术专业工学博士学位.2002年曾在德国斯图加特大学作访问学者.主持省级高校自然科学研究项目或国家自然科学基金多项,并在国内外期刊或学术会议上发表学术论文40余篇,其中第一作者20余篇,在IEEE Transactions on VLSI Systems上发表论文1篇.E-mail:mxyi126@126.com 蒋翠云 女,1962 年生于安徽蚌埠,合肥工业大学副教授,主要研究方向为数值分析、有理逼近、容错计算、内建自测试等. E-mail:hgdyun@foxmail.com A Latching-Window Masking Model Considering Overlapped Transient Pulses in Multi-cycle YAN Ai-bin1,2,LIANG Hua-guo3,HUANG Zheng-feng3,JIANG Cui-yun4,YI Mao-xiang3 (1.SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei,Anhui230009,China; 2.SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei,Anhui230009,China; 3.SchoolofElectronicScience&AppliedPhysics,HefeiUniversityofTechnology,Hefei,Anhui230009,China; 4.SchoolofMathematics,HefeiUniversityofTechnology,Hefei,Anhui230009,China) Technology scaling results in that chip failure caused by single event transient pulses is becoming more and more serious.In order to accurately compute the failure rates introduced by the transient pulses impacting on latches,a novel latching-window masking model considering overlapped transient pulses in multi-cycle is proposed.Firstly,sensitized paths and delays are calculated by the proposed re-convergence aware sensitized path searching algorithm.Further,on re-convergence paths,pulses are overlapped by the proposed pulse overlapping calculation technique.Finally,as regards transient pulses arriving at latches,failure rates are computed by the proposed latching-window masking model.The proposed technique can accurately compute re-convergence induced pulse overlap and it is suitable to estimate failure rates considering multi-cycle.Experimental results for ISCAS'85 benchmarks show that,compared with the approach which has not considered pulse overlap in multi-cycle,the proposed technique improves 7.5% soft error rate accuracy on average with only less than twice the simulation time overhead. latching-window masking;pulse overlap;multi-cycle;re-convergence 2015-01-13; 2016-02-03;责任编辑:梅志强 国家自然科学基金(No.61371025, No.61574052, No.61674048, No.61604001) TP391.72、TN432 A 0372-2112 (2016)12-3011-09 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.12.028

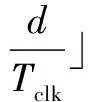
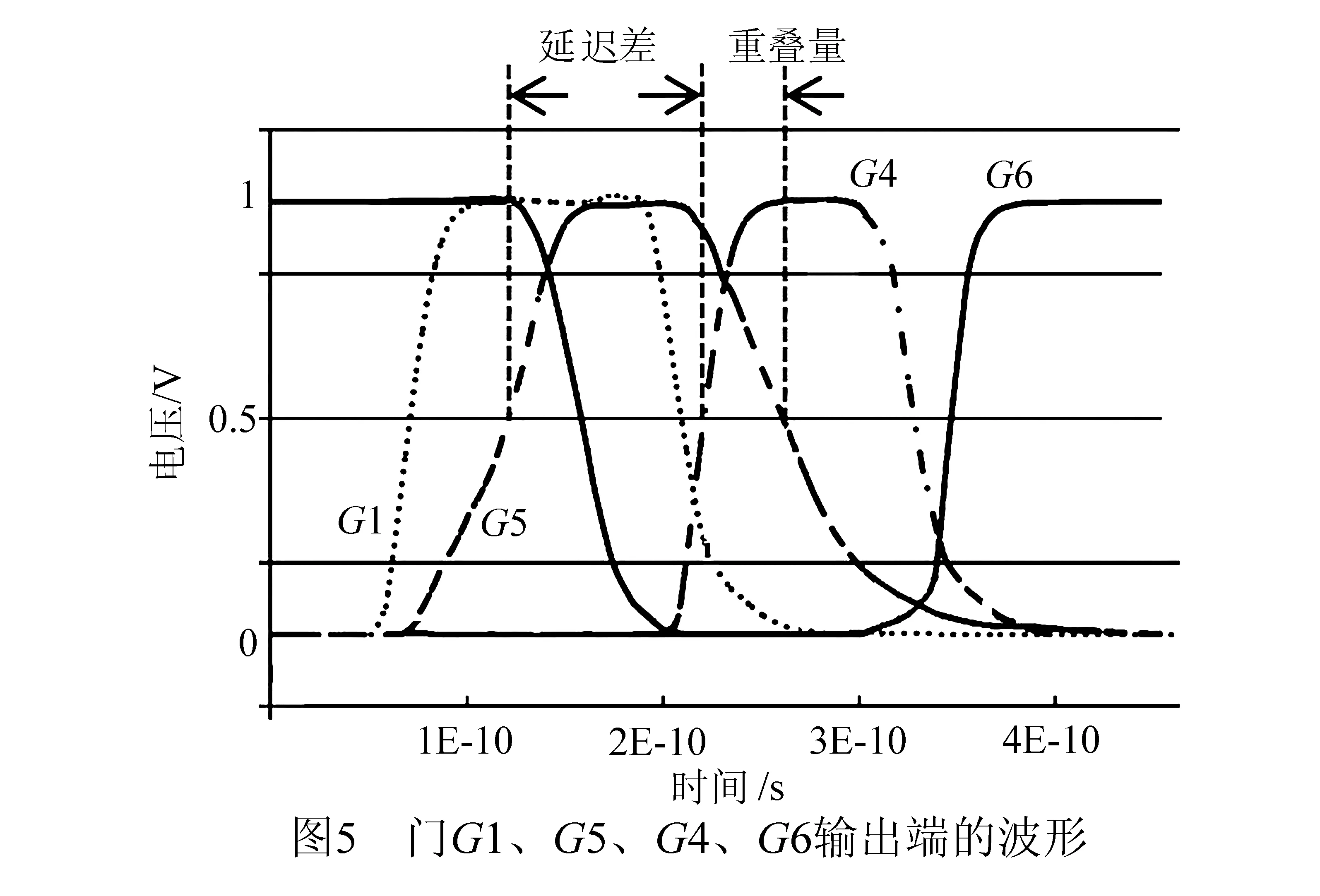
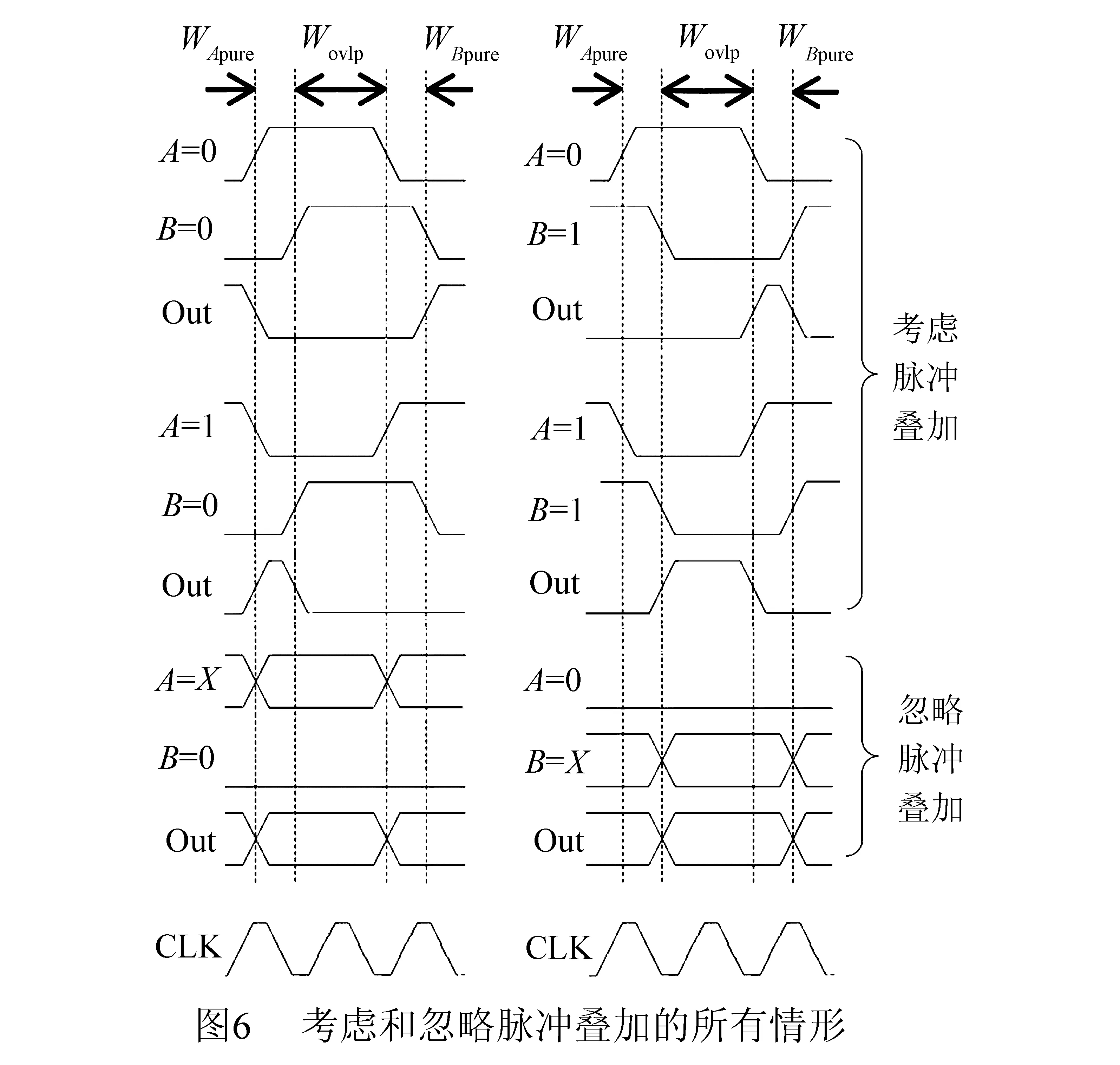
3 本文方案
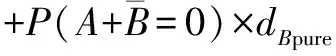

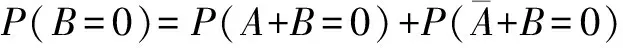
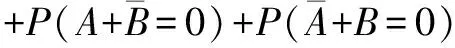
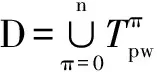

4 实验与结果分析

5 总结






