基于改进粒子群算法的固态变压器在电网中的配置研究

张甦，苗虹，曾成碧

(四川大学电气信息学院, 成都市 610065)

基于改进粒子群算法的固态变压器在电网中的配置研究

张甦，苗虹，曾成碧

(四川大学电气信息学院, 成都市 610065)

作为能源互联网的关键电气设备之一，固态变压器在可再生能源的消纳、电力灵活变换中发挥着重要作用。该文提出在系统中配置固态变压器来解决因大规模分布式电源并网造成的输电线路过载和电压过低问题。在此基础上，采用一种改进粒子群算法对固态变压器的安装位置和容量大小进行优化。最后，在一个4机12节点系统中验证了配置固态变压器能够提升新能源渗透率较高的电网的稳定性和粒子群算法解决固态变压器配置问题的有效性。

能源互联网；固态变压器；分布式电源；粒子群算法

0 引 言

为了更好地将可再生能源接入电网，综合了网络能源技术的能源互联网概念在近年来得到了广泛的关注[1-2]。然而，要实现能源互联网，还面临着诸多技术挑战[3]。固态变压器作为能源互联网的关键装备，直接关系到可再生能源的消纳、电能的灵活高效变换，具有重要的研究价值和应用前景[4]。

固态变压器的研究主要集中在高频变压器和功率器件方面，其面向的应用对象主要是中、高压交流配电网[4-5]。欧盟UNIFLEX-PM(advanced power converters for universal and flexible power management in future electricity networks)项目对固态变压器进行了深入研究，通过它来控制能量的传输和流向，从而实现潮流的优化管理[6]。美国FREEDM(future renewable electric energy delivery and management)项目将固态变压器比作未来能源网中的大脑和路由器，并视固态变压器为构建未来能源互联网的基本模块[4]。瑞士苏黎世联邦理工学院的学者针对固态变压器提出了MEGALink的概念，并进行了深入研究[7-9]。日本在311大地震和核泄漏的灾难之后，成立了“数字电网联盟”，提倡“数字电网”，其核心即利用“数字电网路由器”(电力路由器)统筹管理和调度一定区域范围内的电力[10]。国内的华中科技大学对固态变压器的研究起步较早，并进行了深入研究[11-13]；清华大学提出了一种适用于柔性直流配电网的高频链直流固态变压器[14]。

综上可以看出，现有的研究主要集中在固态变压器的拓扑和控制算法，对于固态变压器在电网中的配置(包括安装位置和容量大小)的研究还比较少。其中，文献[15-16]运用传统的优化算法对FACTS的选址进行优化，文献[17-19]运用遗传算法和粒子群算法分别对FACTS和STATCOM的选址进行研究。

本文首先针对含有大规模可再生能源的电力接入电网以后会大幅降低电网的稳定性甚至危及系统安全的问题，提出在电网中配置固态变压器的解决方案。接着，利用改进粒子群算法求解电网中固态变压器的配置问题。最后以文献[20]中的4机12节点系统为算例，验证配置固态变压器能够提升新能源渗透率较高的电网的稳定性和安全性，同时也验证利用改进粒子群优化算法来解决固态变压器的配置问题的有效性。本文为提高电网对新能源发电系统的消纳能力和固态变压器在电网中的应用提供一条有效途径。

本文分为6个部分。第1部分介绍固态变压器的等效模型；第2部分介绍本文作为仿真算例的4机12节点系统；第3部分提出针对优化问题的目标函数，并对本文所用粒子群优化算法及其改进方法作了简要介绍；第4部分给出运用改进粒子算法优化配置固态变压器的结果，并对结果进行分析；第5部分给出算法改进前、后的效果图并作出分析；第6部分给出本文的主要结论。

1 固态变压器的等效模型

固态变压器由电力电子器件构成的初、次级电力电子变换器，以及联接初、次级的高频变压器构成。根据是否含有直流环节，固态变压器可分为AC/AC型和AC/DC/AC型[21]两种。AC/DC/AC型固态变压器的直流母线环节能为不同类型的分布式电源提供接口，并且初、次级电力电子变换器可以分别控制，是目前主要研究类型[22]。本文也选择该类型的固态变压器为研究对象，其结构如图1所示。

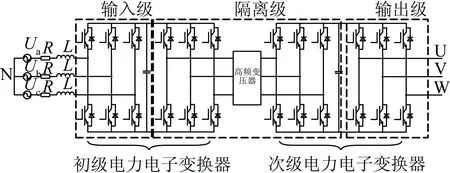
图1 AC/DC/AC型固态变压器

固态变压器的电压变比定义为交流输入、输出的电压幅值之比[23]。改变隔离环节高频变压器的变比即可平滑改变固态变压器的变比。由于输入、输出环节相互隔离，输出电压的相位可以根据需要进行调节，固态变压器能够实现对输入电压幅值、相位甚至频率的变换，从而改变电网潮流。以上功能是传统电力变压器无法实现的。

本文的研究重点为固态变压器的外部特性。根据上述表述建立固态变压器等效模型：

ui=Usin(ωt)

(1)

uo= kUsin(ωt+θ)

(2)

式中：ui为固态变压器的输入电压；uo为固态变压器的输出电压；U为输入电压的幅值；k为固态变压器的变比，θ为固态变压器输入、输出电压的相位差。

通过在线路上配置固态变压器，可以控制线路末端的电压及线路的潮流。图2给出了线路上可以安装固态变压器的2个位置。

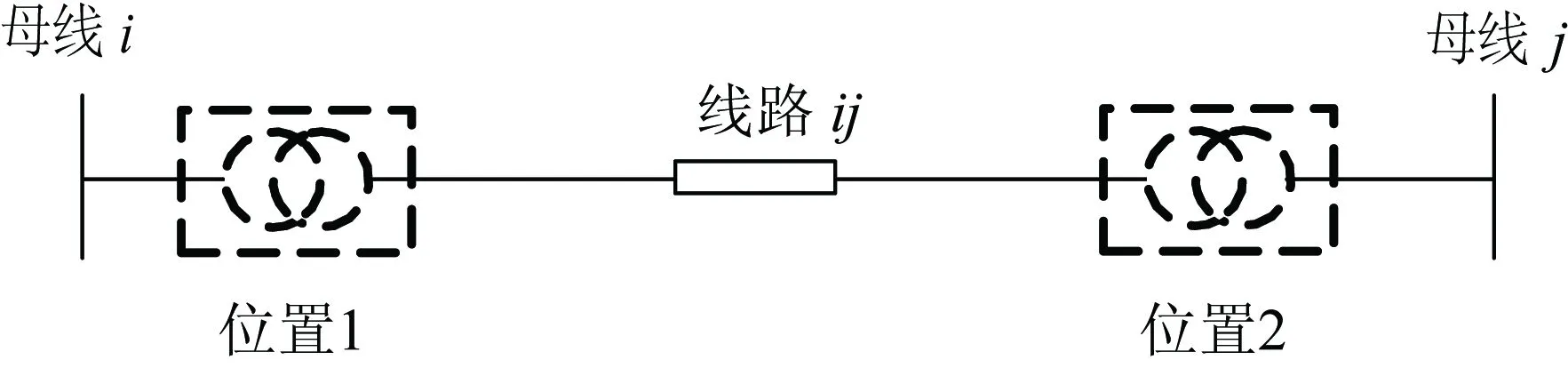
图2 固态变压器可选位置示意图

2 4机12节点系统

本文采用的4机12节点系统图如图3所示[20]。该系统分为3个区域(区域1、2、3)，包含6条230 kV母线、2条345 kV母线和4条22 kV母线。

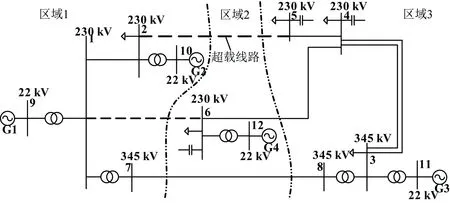
图3 4机12节点系统图

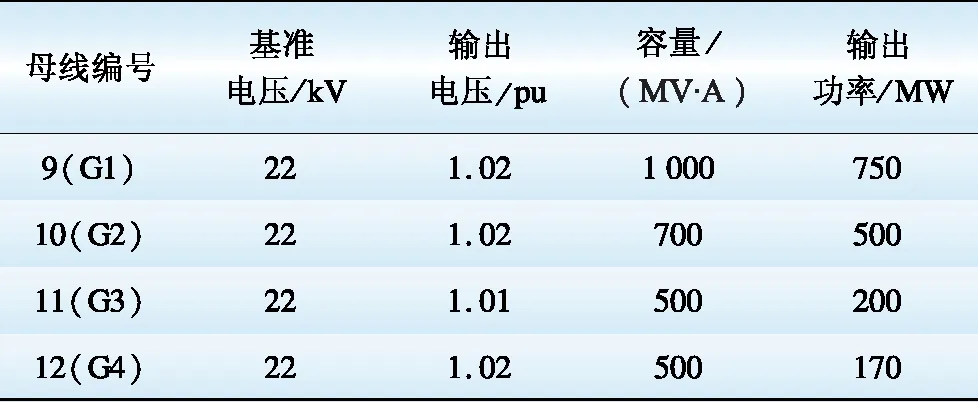
负载参数情况见表1。各发电机组的出力情况见表2。表2中，G1、G2代表水电机组，G3代表火电机组，G4代表风电机组。为了模拟新能源发电的不稳定性对电网造成的影响，假设某时刻G4的出力降为额定容量的30%。系统的输电线路参数以及变压器参数与文献[20]中有关参数相同。

表1 负载参数

Table 1 Parameters of loads

从表1和表2中可以看出，区域1中发电机负荷小，属于能源供应区。区域3中负荷密集，可用发电机组只有火电机组G3，为负荷中心。区域2位于能源供应区和负荷中心之间。当G3无法满足负荷需求时，负荷缺额将通过区域2输送。此外，区域2中只有风力发电机组G4供电，由于风电的出力不稳定，常常无法满足当地的负荷需求，很容易造成区域2中传输线路过载，部分母线电压过低。具体结果将在第4节中说明。

3 模型建立与算法优化

固态变压器的配置的目标主要应该包含以下3个方面：固态变压器的投入成本的最小化、线路负载率的最小化以及全网损耗的最小化。这是一个非线性、非凸的优化问题，再考虑到问题背景是高度非线性的电力系统，因此传统的优化算法处理起来效果非常不理想[19]。本文采用粒子群算法来解决该优化问题。

3.1 目标函数的构造

目标函数构造如下：

J=λ1J1+λ2J2+λ3J3

(3)

式中：J1表征线路负载率情况；J2表征固态变压器的投入成本；J3表征全网损耗情况；λ1、λ2、λ3为权重系数。

J1、J2、J3的表达式如下：

(4)

(5)

J3=Ploss/P

(6)

式中：Mk为第k条线路的负载率；N为输电线路总数；M为需要选址优化的固态变压器的数目；Si为第i台固态变压器的容量；Smax为固态变压器的最大容量[19]；Ploss为全网损耗；P为发电机组输出的总有功功率。

3.2 粒子群算法简介

粒子群算法认为每一个粒子代表着目标函数的一个可能的解。粒子的位置定义如下：

xi=[P1,…,PM]

(7)

(8)

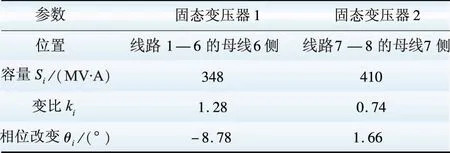
式中：xi代表粒子群中的第i个粒子的位置；Pi(i=1, 2, ...，M)为第i个固态变压器的参数向量；ωi表示第i个固态变压器的位置；Si表示第i个固态变压器的容量；ki表示第i个固态变压器的变比；θi表示第i个固态变压器的输入、输出电压的相位差。

粒子的速度和位置在每次迭代之后都会更新[19]。粒子的速度、位置更新公式为：

vi(t)=wtvi(t-1)+c1r1[xi,best-xi(t)]+

c2r2[xg,best-xi(t)]

(9)

xi(t)=xi(t-1)+vi(t)

(10)

式中：vi(t)为第i个粒子在第t次迭代时的速度；wt表示在第t次迭代时的惯性权重；c1、c2分别为个体和群体加速度因子；r1和r2是分布于[0,1]区间的随机数；xi,best表示第i个粒子的个体历史最优位置，xg，best表示粒子群中所有粒子的历史最优位置。

粒子的速度和位置由式(9)—(10)的反复迭代更新，直到达到最大迭代次数或者达到期望值，最后得到的xg，best即为固态变压器优化配置问题的解。

3.3 约束条件

为了避免粒子盲目搜索，同时考虑到电力系统的实际限制，需要对粒子的位置和速度进行约束。由于每台固态变压器在线路上的安装位置有2处，因此总共可以选择的安装位置应该有16处。另外，需要注意的是同一位置每次只能安装1台固态变压器。粒子的位置约束条件如下：

(11)

速度约束条件如下：

(12)

此外在电网环境下所得结果还应该受电网约束：

(13)

Uk为母线电压的标幺值，ηh表示G1—G4所连4台变压器的负载率，ξi表示固态变压器的负载率。如果不满足式(13)中的任一约束条件，那么J将趋于正无穷大。

3.4 改进的粒子群算法

粒子群算法的惯性权重w体现的是粒子继承先前速度的能力。较大的惯性权重有利于全局搜索，而较小的惯性权重则更利于局部搜索。w保持不变的粒子群算法虽然具有较快的收敛速度，但后期容易陷入局部最优解，求解精度低。为了更好地平衡算法的全局搜索和局部搜索能力，避免陷入局部最优解，本文在迭代过程中动态地改变惯性权重值[24]。即

w(t)=wstart-(wstart-wend)(t/Tmax)2

(14)

式中：wstart为初始惯性权重；wend为迭代至最大次数时的惯性权重；t为当前迭代数；Tmax为最大迭代次数。

4 仿真结果与分析

未配置固态变压器时，对图3所示网络的自然潮流分布情况进行计算。各节点电压的情况如图4所示。各传输线路的负载率如图5所示(优化前)。图5中传输线编号的含义见表3。从图4和图5中可以看出，G4出力不足(170MW)时，母线4、5的电压均低于0.95pu，线路1—6和2—5超载。

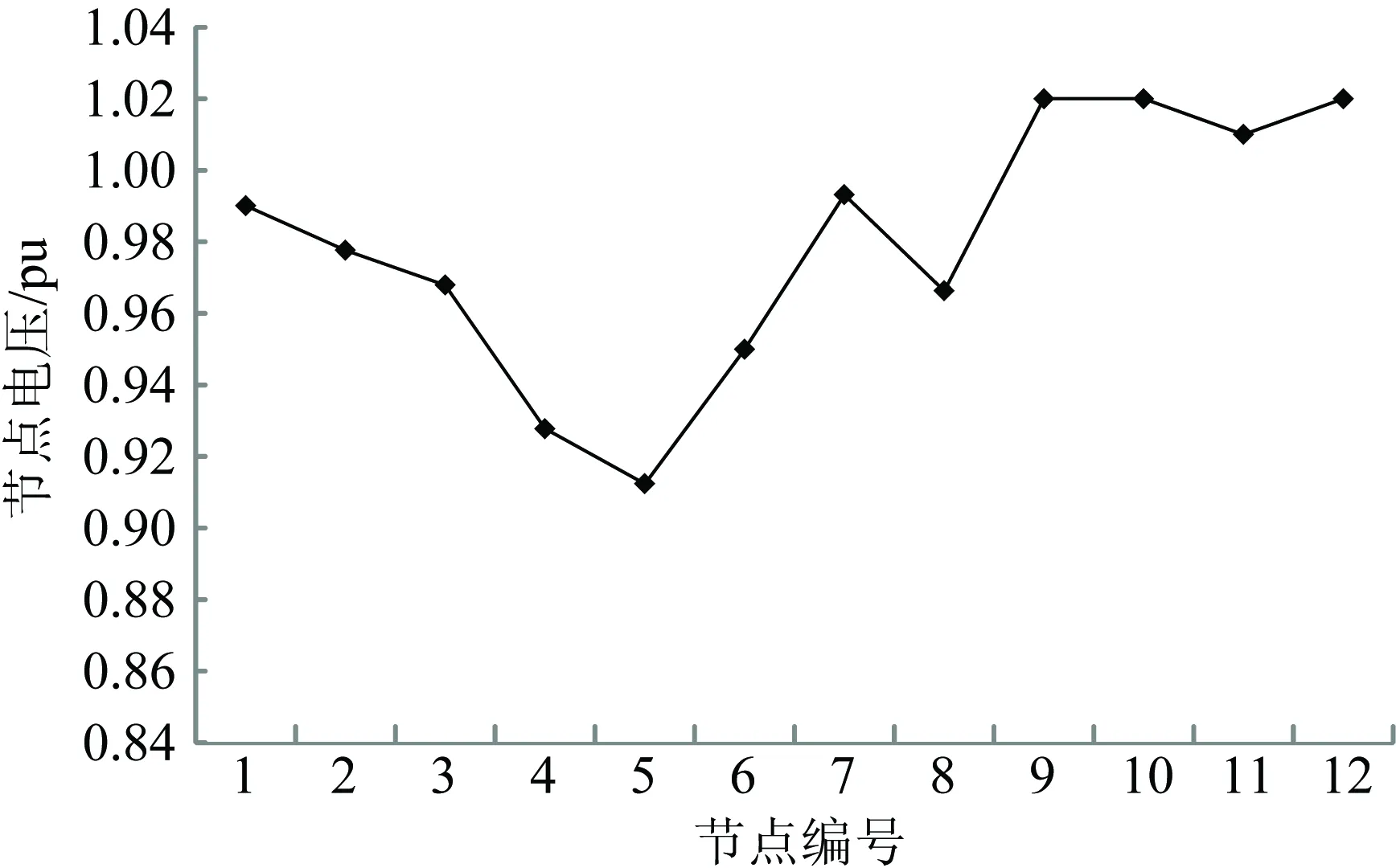
图4 自然潮流时各节点电压情况

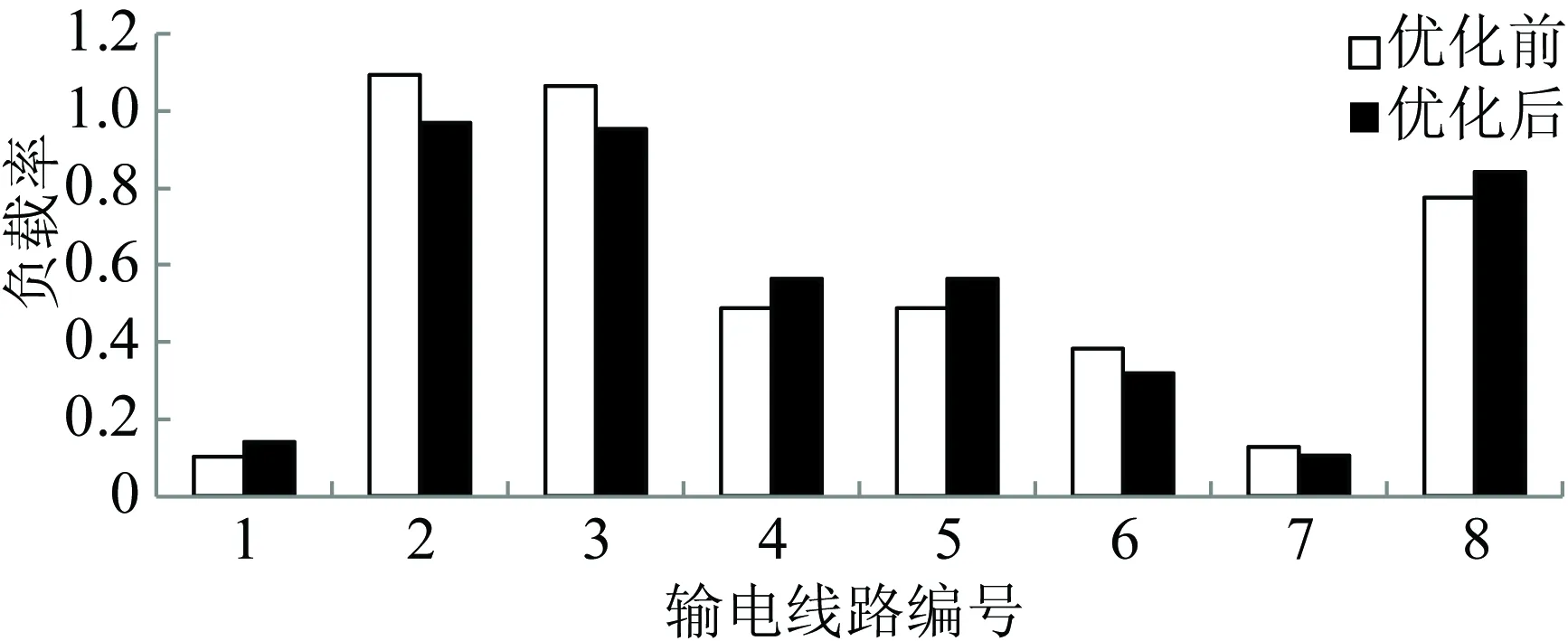
图5 方案1加入固态变压器前后线路负载率对比

表4 算法所需参数

为了解决上述问题，本文在该网络中配置2台固态变压器。此外，本文设计了3个方案，在每个方案中对优化目标选择了不同的权重值，并对3个方案进行了仿真。仿真过程所需要的参数见表4(粒子群算法粒子数目n取为20)。

4.1 方案1(λ1=λ2=λ3=1)

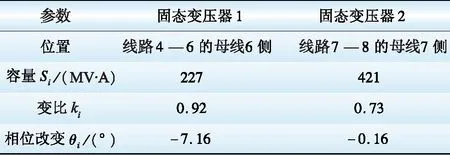
该方案中线路负载率、固态变压器成本、全网损耗3个目标同等重要。固态变压器的配置结果见表5。线路负载率如图5所示。各节点的电压情况如图6所示。

表5λ1=λ2=λ3=1时的配置结果

Table 5 Configuration ofλ1=λ2=λ3=1

从图5中可以很直观地看到加入固态变压器后，过载线路的潮流得到了有效转移，系统中线路过载的问题得到了解决。

4.2 方案2(λ1=1，λ2=100，λ3=80)

方案2更多地考虑电网运行的经济性(固态变压器成本为主，全网损耗次之)。固态变压器配置结果见表6。各节点电压和线路负载率如图6—7所示。

表6λ1=1，λ2=100，λ3=80时的配置结果

Table 6 Configuration ofλ1=1，λ2=100，λ3=80

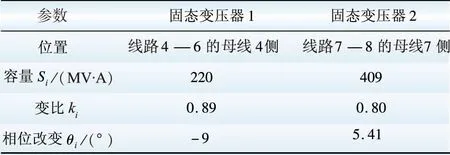
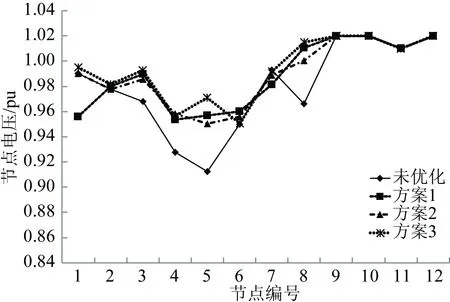
图6 自然潮流及3种方案节点电压对比

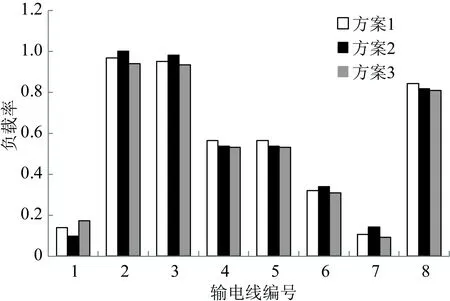
图7 3种方案线路负载率对比

4.3 方案3(λ1=100，λ2=λ3=1)

方案3表示更多地考虑电网运行的安全性，尽可能降低线路的负载率。固态变压器配置结果见表7。各节点电压和线路负载率如图6—7所示。

表7λ1=100，λ2=λ3=1时的配置结果

Table 7 Configuration ofλ1=100，λ2=λ3=1

4.4 方案结果分析

3种方案自然潮流状态下的节点电压情况如图6所示。从图6可以看出，配置固态变压器以后母线4、5的低电压问题得到了解决。母线9—12由于直接连接发电机，又因发电机具有电压控制环节，这4条母线的电压始终保持恒定。

图7为3种方案中输电线路的负载率。从表4和表6可以看出，采用侧重经济效益的方案2时，虽然固态变压器的容量相比方案1有所降低，但部分线路负载率有所上升，线路2的负载率甚至达到承载极限，严重威胁电网的安全运行，如图7所示。另外，从图7中还可以看出，方案3侧重线路安全，并尽可能降低了线路负载率，但对比表7和表4中可以发现，所需的固态变压器容量上升，导致成本增加。

5 算法改进前后对比

图8是以方案2为例分别采用常规粒子群算法和改进后的粒子群算法的优化迭代过程。从图8中可以看到，采用改进后的粒子群算法相比于常规粒子群算法虽然前期收敛速度较慢，但在后期局部搜索能力增强，收敛速度加快，跳出了局部最优的困境，能够求得更优的解(更小的目标函数值)。

从图8中还可以看到，改进后的算法从第100次迭代以后群体最优解的位置和目标函数值已不再变化，又由于这是一个高度非线性、非凸优化问题，我们无法得知目标函数准确的最小值，因此可以认为粒子群算法已收敛至最接近目标函数最小值的位置。同理，改进前的常规粒子群算法从第220次迭代以后群体最优解的位置和目标函数值也不再变化，因此可以认为算法已收敛至终值。

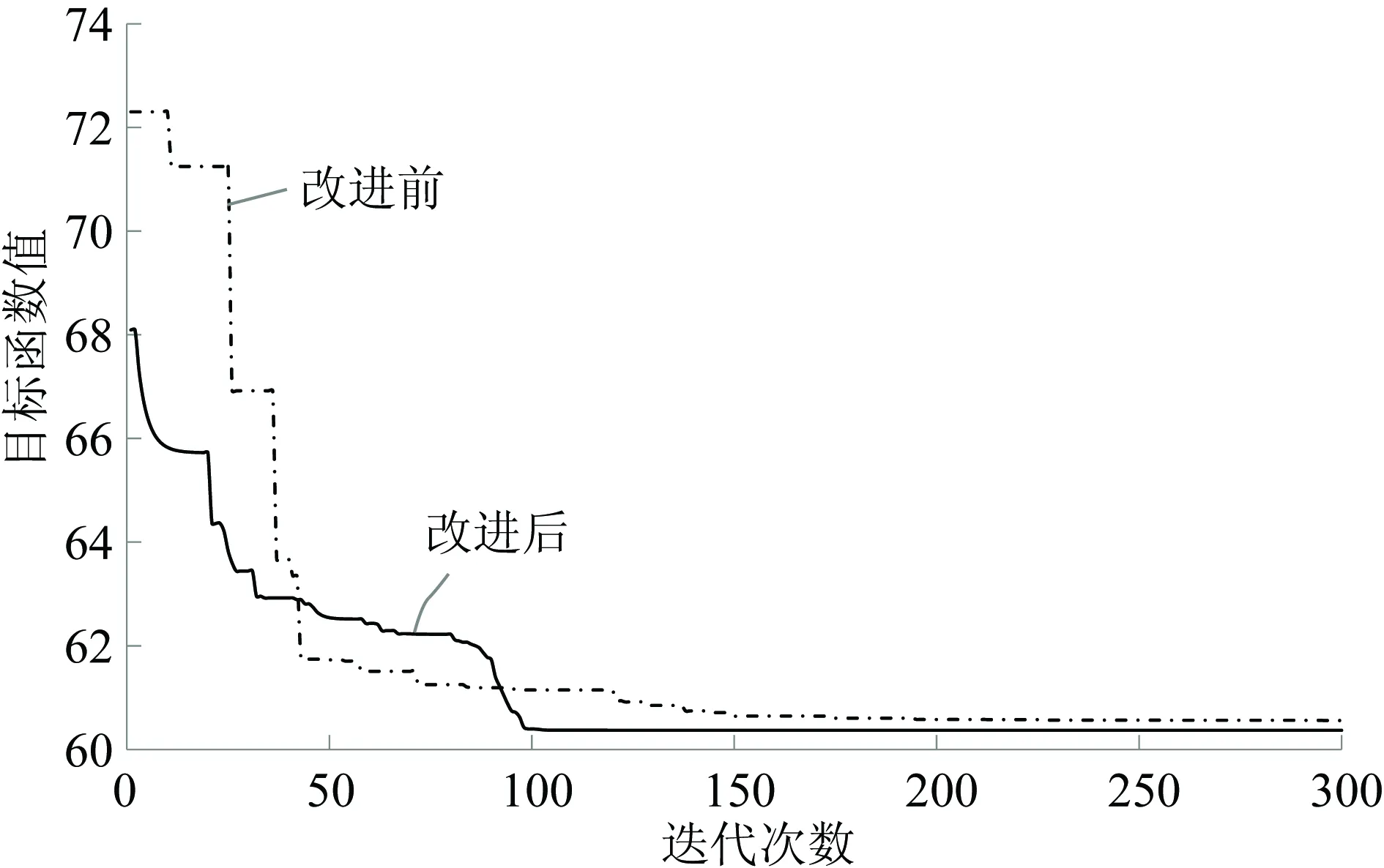
图8 算法改进前后的效果对比

6 结 论

新能源渗透率较高的电网中容易出现线路过载和部分母线电压过低的问题，本文提出了配置固态变压器以变更潮流的方法来解决。在此基础上，采用改进粒子群算法对固态变压器的选址和容量进行优化，最后在4机12线系统中进行了验证。本文提出的固态变压器配置方法对固态变压器的发展及其在电力系统中的应用起到了一定的促进作用。本文主要得到了如下结论：

(1)固态变压器在被优化配置后，潮流从过载线路转入了未过载线路，解决了系统线路过载和部分母线电压低于规定值的问题，提高了电网的安全性和稳定性。

(2)目标函数中选择不同的权重影响着算法寻优的方向。

(3)在算法迭代过程中使用变惯性权重的做法有利于提高算法求解精度。

[1]刘振亚. 全球能源互联网[M]. 北京: 中国电力出版社, 2015.

[2]刘开俊. 能源互联网发展路径探究[J]. 电力建设,2015,36(10):5-10. LIU Kaijun. Development path exploration of energy internet[J]. Electric Power Construction, 2015,36(10):5-10.

[3]田世明，栾文鹏，张东霞，等. 能源互联网技术形态与关键技术[J]. 中国电机工程学报, 2015,35(14): 3482-3494. TIAN Shiming, LUAN Wenpeng, ZHANG Dongxia, et al. Technical forms and key technologies on energy internet [J]. Proceedings of the CSEE, 2015, 35(14): 3482-3494.

[4]陈宇，韩民晓，王皓界，等. 基于模块化三电平方式的中压直流配电网DC/DC换流器设计[J]. 电力建设,2016,37(5):69-77. CHEN Yu, HAN Minxiao, WANG Haojie, et al. DC/DC converter design of MVDC distribution network based on modular three-level[J]. Electric Power Construction, 2016,37(5):69-77.

[5]曹军威，孟坤，王继业，等. 能源互联网与能源路由器[J]. 中国科学:信息科学,2014,44(6): 714-727. CAO Junwei, MENG Kun, WANG Jiye, et al. Energy internet and energy router[J]. Science in China: Information Science. 2014, 44(6): 714-727.

[6]ALMALEKI M, WHEELER P, CLARE J. Sliding mode observer design for universal flexible power management (Uniflex-PM) structure[C] // Proceedings of the 34th Annual Conference of IEEE Industrial Electronics (IECON)．Orlando，FL：IEEE，2008：3321-3326．

[7]GUILLOD T, HUBER J, ORTIZ G, et al. Characterization of the voltage and electric field stresses in multi-cell solid-state transformers[C]// Proceedings of the IEEE Energy Conversion Congress and Exposition．Pittsburgh，PA：IEEE，2014：4726-4734.

[8]GEIDL M, KOEPPEL G, FAVRE-PERROD P, et al. Energy hubs for the future[J]. IEEE Power and Energy Magazine，2007, 5(1): 24-30

[9]SCHULZE M, FRIEDRICH L, GAUTSCHI M. Modeling and optimization of renewables: applying the energy hub approach[C]// Proceedings of the IEEE International Conference on Sustainable Energy Technologies．Singapore：IEEE，2008：83-88.

[10]冯宇鹏，吴金龙，王先为，等. 电网不平衡故障下电力电子变压器控制策略[J]. 电力建设,2016,37(7):84-90. FENG Yupeng, WU Jinlong, WANG Xianwei, et al. Control strategy of power electronic transformer under unbalanced grid fault[J]. Electric Power Construction, 2016,37(7):84-90.

[11]王丹，毛承雄，陆继明. 自平衡电子电力变压器[J]. 中国电机工程学报,2007, 27(6): 77-83. WANG Dan, MAO Chengxiong, LU Jiming. Auto-balancing electronic power transformer[J]. Proceedings of the CSEE, 2007, 27(6): 77-83.

[12]成建鹏，毛承雄，范澍，等. 电子电力变压器原理和仿真研究[J]. 电力自动化设备,2004, 24(12): 23-25. CHENG Jianpeng, MAO Chengxiong, FAN Shu, et al. Principle of electronic power transformer and its simulation study[J]. Electric Power Automation Equipment, 2004, 24(12): 23-25.

[13]王丹，毛承雄，陆继明，等. 基于电子电力变压器的电能质量调节方法[J]. 高电压技术,2005, 31(8): 63-65. WANG Dan, MAO Chengxiong, LU Jiming, et al. Electronic power transformer-based power quality control method[J]. High Voltage Engineering, 2005, 31(8): 63-65.

[14]赵彪，宋强，刘文华，等. 用于柔性直流配电的高频链直流固态变压器[J]. 中国电机工程学报，2014, 34(25): 4295-4303. ZHAO Biao, SONG Qiang, LIU Wenhua, et al. High-frequency-link DC solid state transformers for flexible DC distribution [J]. Proceedings of the CSEE，2014, 34(25): 4295-4303.

[15]YORINO N, EL-ARABY E, SASAKI H, et al. A new formulation for FACTS allocation for security enhancement against voltage collapse[J]. IEEE Transactions on Power Systems, 2003, 18(1): 3-10.

[16]LIMA F G, GALIANA F D, KOCKAR I, et al. Phase shifter placement in large-scale systems via mixed integer linear programming[J]. IEEE Transactions on Power Systems, 2003, 18(3): 1029-1034.

[17]GERBEX S, CHERKAOUI R, GERMOND A. Optimal location of multi-type FACTS devices in a power system by means of genetic algorithms[J]. IEEE Transactions on Power Systems, 2001, 16(3): 537-544.

[18]ONGSAKUL W, JIRAPONG P. Optimal allocation of FACTS devices to enhance total transfer capability using evolutionary programming[C]// Proceedings of the IEEE International Symposium on Circuits and Systems．Japan：IEEE，2005：4175-4178.

[19]DEL V Y, HARLEY R G, VENAYAGAMOORTHY G K. Comparison of enhanced-PSO and classical optimization methods: a case study for STATCOM placement[C]// Proceedings of the International Conference on Intelligent System Applications to Power Systems．UK：IEEE，2005：1-7.

[20]JIANG S, ANNAKKAGE U D, GOLE A M. A platform for validation of FACTS models[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 484-491.

[21]凌晨，葛宝明，毕大强. 配电网中的电力电子变压器研究[J]. 电力系统保护与控制，2012，40(2): 34-39. LING Chen, GE Baoming, BI Daqiang. A power electronic transformer applied to distribution system[J]. Power System Protection and Control，2012，40(2): 34-39.

[22]宗升，何湘宁，吴建德，等. 基于电力电子变换的电能路由器研究现状与发展[J]. 中国电机工程学报，2015，35(18): 4559-4570. ZONG Sheng, HE Xiangning, WU Jiande, et al. Overview of Power Electronics Based Electrical Energy Router[J]. Proceedings of the CSEE，2015，35 (18): 4559-4570.

[23]张晓东. 电力电子变压器及其在电力系统中的应用[D]. 济南: 山东大学, 2012. ZHANG Xiaodong. Power electronic transformer and its application in power system[D]. Jinan: Shandong University, 2012.

[24]沙熠，邱晓燕，宁雪姣，等. 协调储能与柔性负荷的主动配电网多目标优化调度[J]. 电网技术，2016，40(5): 1394-1399. SHA Yi, QIU Xiaoyan, NING Xuejiao, et al. Multi-objective optimization of active distribution network by coordinating energy storage system and flexible load [J]. Power System Technology，2016，40(5): 1394-1399.

(实习编辑 郭文瑞)

Solid State Transformer Configuration in Power Grid Based on Improved Particle Swarm Optimization Algorithm

ZHANG Su, MIAO Hong, Zeng Chengbi

(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)

Solid state transformer is one of the key technologies of the energy internet, which plays an important role in the acceptance of renewable energy and flexible power conversion. This paper proposes that installing solid state transformers in the system can solve the problem that when large scale of distributed generators are connected into power grid, it may cause overloaded lines and low voltage buses. On this basis, this paper introduces the improved particle swarm optimization algorithm to determine the optimal location and size of solid state transformers. Finally, the simulation results in a 4 machines and 12 buses power system verify that solid state transformers can improve the stability and safety of power grid with high penetration of new energy, and it is effective to use particle swarm optimization algorithm to solve the configuration problem of solid state transformer.

energy internet; solid state transformer; distributed generator; particle swarm optimization algorithm

国家重点基础研究发展计划项目(973计划)(2012CB215200)；四川省科技支撑项目(2014GZ0069)；成都市科技局项目(2015-HM01-00535-SF); 四川省科技厅项目(能源互联网中固态变换器关键技术研究)

TM 46

A

1000-7229(2016)11-0071-07

10.3969/j.issn.1000-7229.2016.11.011

2016-06-15

张甦(1991)，男，硕士研究生，研究方向为分布式发电和微电网技术;

苗虹(1971)，女，副教授，通讯作者，研究方向为分布式发电和微电网技术；

曾成碧(1970)，女，副教授，研究方向为能量转化技术的智能控制。

Project supported by the National Basic Research Program of China (973 Program) (2012CB215200)