采用高低匹配机制的发电权交易市场中发电公司的竞价策略

蒙文川，林昶咏，文福拴，吴鸿亮，宋艺航，张翔

(1.直流输电技术国家重点实验室(南方电网科学研究院有限责任公司)，广州市 510080；2. 浙江大学电气工程学院, 杭州市 310027)

采用高低匹配机制的发电权交易市场中发电公司的竞价策略

蒙文川1，林昶咏2，文福拴2，吴鸿亮1，宋艺航1，张翔1

(1.直流输电技术国家重点实验室(南方电网科学研究院有限责任公司)，广州市 510080；2. 浙江大学电气工程学院, 杭州市 310027)

发电权交易有利于优化电源结构，促进节能减排，在国内电力系统领域得到比较普遍的应用。发电公司在发电权交易市场中所采用的竞价策略直接影响其收益，因而是发电公司关注的重要问题。在此背景下，针对采用高低匹配机制的发电权集中竞价交易市场，发展了计及风险的发电公司的竞价策略。首先，建立了评估发电权交易双方的成本和收益的数学模型。之后，构建了发电公司参与采用高低匹配机制的发电权交易市场的计及风险的最优竞价策略的优化模型, 并采用蒙特卡洛仿真方法求解。最后，用算例对所构造的最优竞价策略模型和采用的方法进行说明，并分析了发电权交易其他参与者的报价行为对所研究的发电公司最优报价策略的影响。

发电权交易; 竞价策略; 高低匹配; 蒙特卡洛仿真

0 引 言

自2008年3月国家电力监管委员会颁布《发电

权交易监管暂行办法》以来，发电权交易已在全国诸多省市实施。发电权交易是极具中国特色的电力市场交易的组成部分，其所涉及的竞价、撮合、双边交易等交易机制与电能市场交易、辅助服务市场交易等类似，但在撮合方式、竞价策略、风险评估等方面有些区别。

发电权交易模式主要包括集中竞价和双边交易两大类。不管采用怎样的交易模式，参与发电权交易的发电机组都可分为发电权出让方和受让方两大类。在发电权交易中，出让方与受让方的概念是针对“发电权”买卖而言的[1]。发电权出让方指被替代发电的机组，一般是小容量或高能耗机组，在交易中出让发电权，实际发电量减少或完全不发电；发电权受让方是替代发电的机组，一般是大容量机组或环保机组，在交易中购买发电权，实际发电量增加。在最终结算时，首先由电网公司按照出让方的上网电价与出让方进行结算，再由出让方按照发电权交易合约向受让方完成支付，故发电权出让方希望发电权最终结算价格越低越好，而发电权受让方希望发电权结算价格越高越好。发电权交易的出让方与受让方的概念不同于一般商品买卖交易。发电权出让方应该理解为电量的买方，相当于从受让方机组买电上网。

现有的针对发电权交易的研究主要集中在发电权交易模式、机制设计、竞价策略、计及发电权交易的电力系统运行等方面。文献[2]探讨了发电权集中竞价模式和双边交易模式在电力市场中的协调方法，设计并比较了10种发电权集中竞价模型。文献[3]在考虑了交易成本的前提下设计了一种激励相容的发电权集中竞价交易模式，并用算例说明了其优化资源配置的效果。文献[4]构造了计及发电权交易的电力系统阻塞调度模型，并对分别以最大化社会效用、最大化成交量、考虑能耗约束的最大化成交量作为发电权交易的目标函数的情形做了比较分析。文献[5]针对风火发电权交易构建了多买方平台，并采用风险管控理论和委托代理机制构建了风火发电权交易模型。

针对电力市场中的竞价策略问题，现有的研究工作主要集中在日前能量市场、辅助服务市场等方面。构建竞价策略的主要目标是在可接受的风险水平下最大化收益。文献[6-8]研究了发电公司在不完全竞争的电力市场中的竞价策略，构建了多种适用于不同情形的发电公司计及风险的最优竞价策略模型框架，考虑了交易收益与交易风险之间的协调。文献[9]研究了发电公司在备用市场的竞价策略，考虑了备用容量需求的不确定性。

到目前为止，针对发电权交易策略的研究主要集中于构建在发电权集中竞价市场中的竞价策略与在双边合同市场中的谈判策略。文献[10]在机会约束规划框架下构建了发电权交易的竞价模型，并采用双层嵌套方法求解。文献[11]针对不完全信息情形，运用贝叶斯学习及Zeuthen策略分析了发电权双边交易模式下的发电公司谈判策略，具有较高的谈判效率。

高低匹配机制由于可以在相当程度上限制发电公司行使市场势力，在市场机制尚不完善的电力市场环境下具有明显的优势，在我国这一轮电力市场改革中受到了比较广泛的重视。文献[12]介绍了高低匹配机制的基本原理及其在区域电力市场中运用的合理性。文献[13]建立了高低匹配与统一出清2种价格机制下的发电权交易竞价模型。文献[14]研究了高低匹配机制下区域发电权交易的社会效益，说明了该机制可以在发电权出让方与受让方之间实现社会效益的平等分配，同时可以明确输电成本和网损费用的分摊主体。

就我们所知，针对采用高低匹配机制的发电权交易市场中发电公司最优报价策略问题的研究尚相当初步，且没有详细描述交易风险。在上述背景下，本文针对采用高低匹配机制的发电权交易市场中的发电公司竞价策略进行探讨，构建考虑不确定因素的竞价策略优化模型，采用蒙特卡洛模拟方法求解，并用算例对所构造的模型和采用的方法做了说明。

1 发电权交易双方成本与收益模型

1.1 发电权交易成本模型

考虑参与发电权交易的发电机组所处地理位置时，单位电量的发电权交易成本Cij主要包括2部分[15]。

(1)交易固定成本Cij,con，即发电权交易中的交易佣金，与机组所在地理位置无关。

(2)交易地域成本Cij,reg，用于反映发电权交易引起系统潮流变化对网损和输电成本所带来的影响。若发电权交易能起到就近电力电量平衡、降低输电线路负荷等积极作用，则地域交易成本就低甚至可能为负值，则该笔发电权交易就应该受到鼓励。反之，若该笔发电权交易加大了系统网损和输电成本，甚至导致潮流越限等情况，此时地域交易成本就很高。位于同一节点的发电机组之间的发电权交易的地域成本为0。

以一个简单的3节点电力系统为例，进一步说明发电权交易地域成本的意义。

对于图1所示的3节点电力系统，如果位于节点A的机组的发电权出让给位于节点B或节点C的机组，则节点B或节点C的负荷可以实现就地平衡，对于减轻线路潮流具有积极作用，故位于节点A的机组与位于节点B或C的机组之间的发电权交易的地域成本Cij,reg很低，甚至可能为负值。位于同一节点的发电机组之间所开展的发电权交易对系统潮流没有影响，相关交易的地域成本为0。另一方面，如果位于节点B或节点C的机组的发电权出让给位于节点A的机组，则线路潮流会加重，此时就存在地域成本，从而就需要确保发电权交易产生的社会效益足以弥补所导致的地域成本。

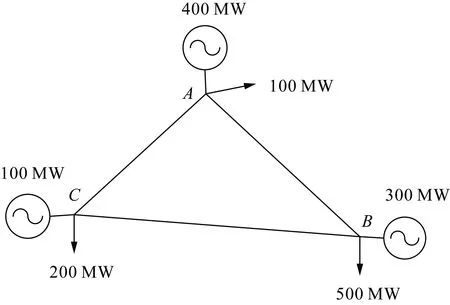
图1 3节点电力系统

1.2 发电权交易的社会福利模型

假设：(1)在发电权交易市场中有n台机组出让发电权，m台机组受让发电权；(2)第i台出让发电权的发电机组的报价及申报出让发电权电量分别为Psell,i和Qsell,i，第j台受让发电权的发电机组的报价及申报收购发电权电量分别为Pbuy,j和Qbuy,j；(3)第i台出让机组和第j台受让机组经撮合形成发电权交易，该笔交易的发电权成交价格及交易电量分别为Pij和Qij；(4)发电权交易涉及的单位电量交易成本为Cij。在上述假设下，该发电权交易的社会福利Uij可用式(1)[16]计算：

Uij=(Psell,i-Pbuy,j-Cij)Qij

(1)

1.3 发电权出让方收益模型

发电权出让方的收益指其在发电权交易中获得的收益，其可能高于也可能低于机组自己发电上网的收益。对于第i台发电权出让机组，假设其上网电价及单位发电成本分别为Rsell,i和Csell,i。发电权交易中买卖双方地位均等，交易成本由双方均摊。在发电权交易中，只有出让方机组的收益大于0时，其才有可能参与发电权交易[17]。这样，对于任意一笔发电权交易，成交价格都必须低于出让方上网电价。当发电权成交价格低于其上网电价一定幅度时，发电权出让方就有获利空间。发电权交易的获利空间指发电权出让方参与发电权交易不至于亏损的价格底线，在该价格范围内报价并不一定会让发电权出让方机组在发电权交易中获得比原先自身发电上网的收益更多，但可保证机组参与发电权交易时不至于亏损。

发电权出让方的报价底线满足：

(2)

考虑发电权交易成本后，出让方机组i的发电权交易收益gsell,i为

(3)

在高低匹配机制下，发电权成交价格Pij为双方报价的均值[18]，即

(4)

由式(3)和式(4)可得：

(5)

1.4 发电权受让方收益模型

发电权受让方收益指其参与发电权交易后，与没有参与发电权交易时相比多发电所获得的额外收益。对于第j台发电权受让机组，假设该机组的上网电价和单位发电成本分别为Rbuy,j和Cbuy,j。对于任一笔发电权交易，发电权成交价格都必须高于受让方相应的发电成本，即让发电权受让方有获利空间：

(6)

考虑发电权交易成本后，受让方机组j的发电权交易收益gbuy,j为

(7)

2 发电权交易竞价策略模型

对于给定时段的发电权交易，通过式(1)，(5)，(7)可以直接求出该笔发电权交易下的社会福利水平及参与发电权交易双方的收益。不过，就构造发电公司参与发电权交易的竞价策略而言，任意一次交易的收益情况并没有太大价值，因为其无法指导发电机组在发电权竞价市场的策略性报价。本节构建发电权交易双方的预期收益模型，并在此基础上发展发电机组竞价策略。

2.1 预期收益最大化的发电权竞价模型

以第i台发电权出让机组为研究对象，由式(3)可知，其发电权交易收益gsell,i与其自身报价、其他所有与其进行发电权交易的受让方机组报价及每笔发电权交易的成交量有关。由1.3节中对发电权交易出让机组的分析可知，其在发电权交易中的报价不是任意的。为保证机组在发电权交易中不至于亏损，其报价需要受其上网电价的限制，即需要考虑报价约束。这样，在考虑报价约束的情况下，最大化出让方机组i的预期收益问题可用下述优化模型描述：

(8)

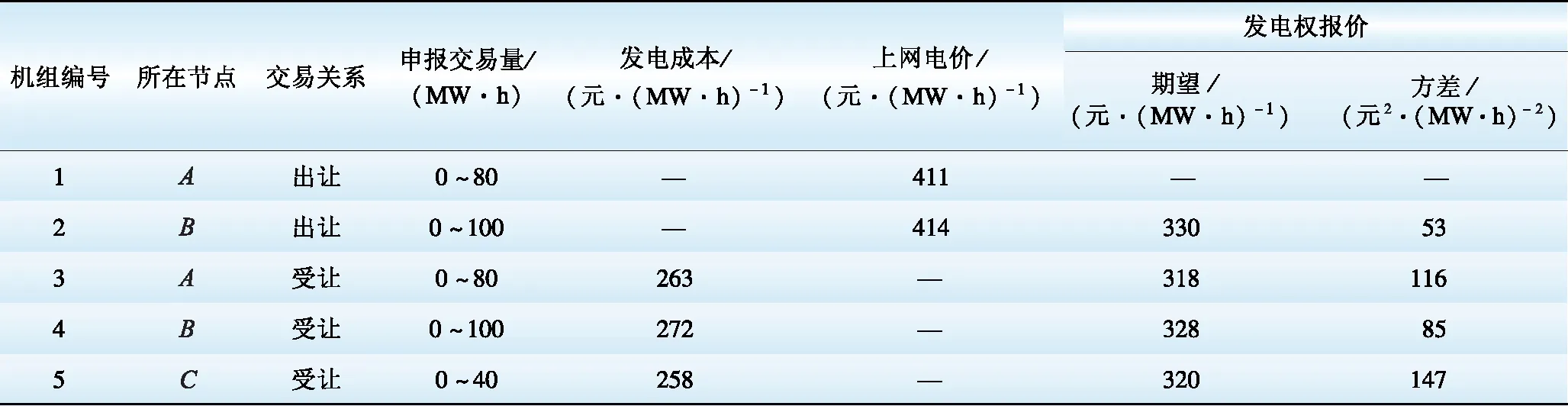
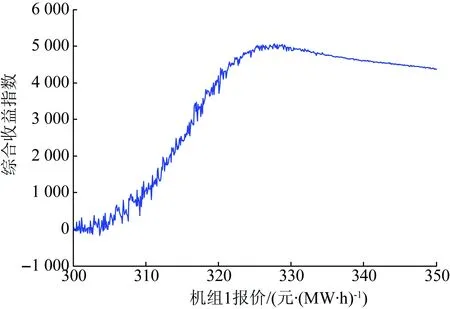
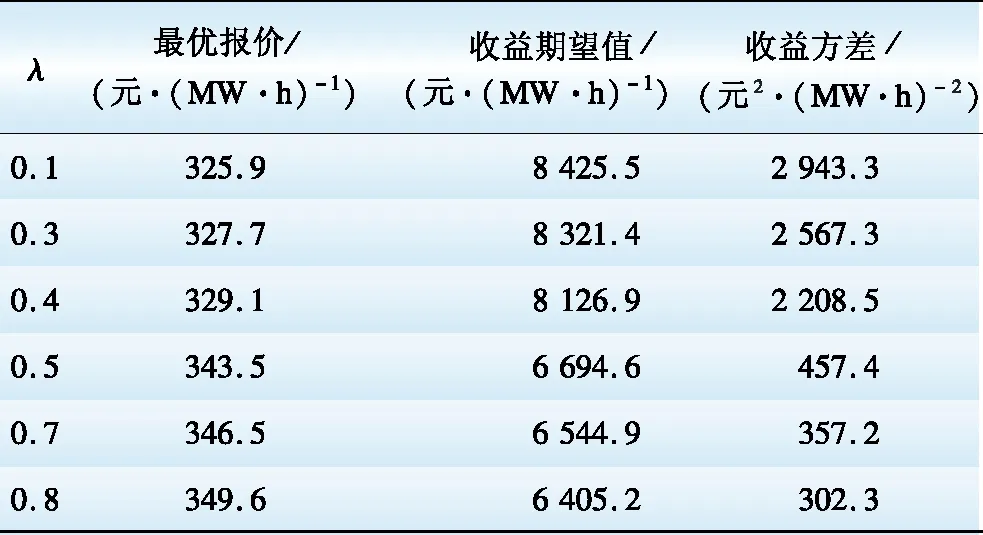
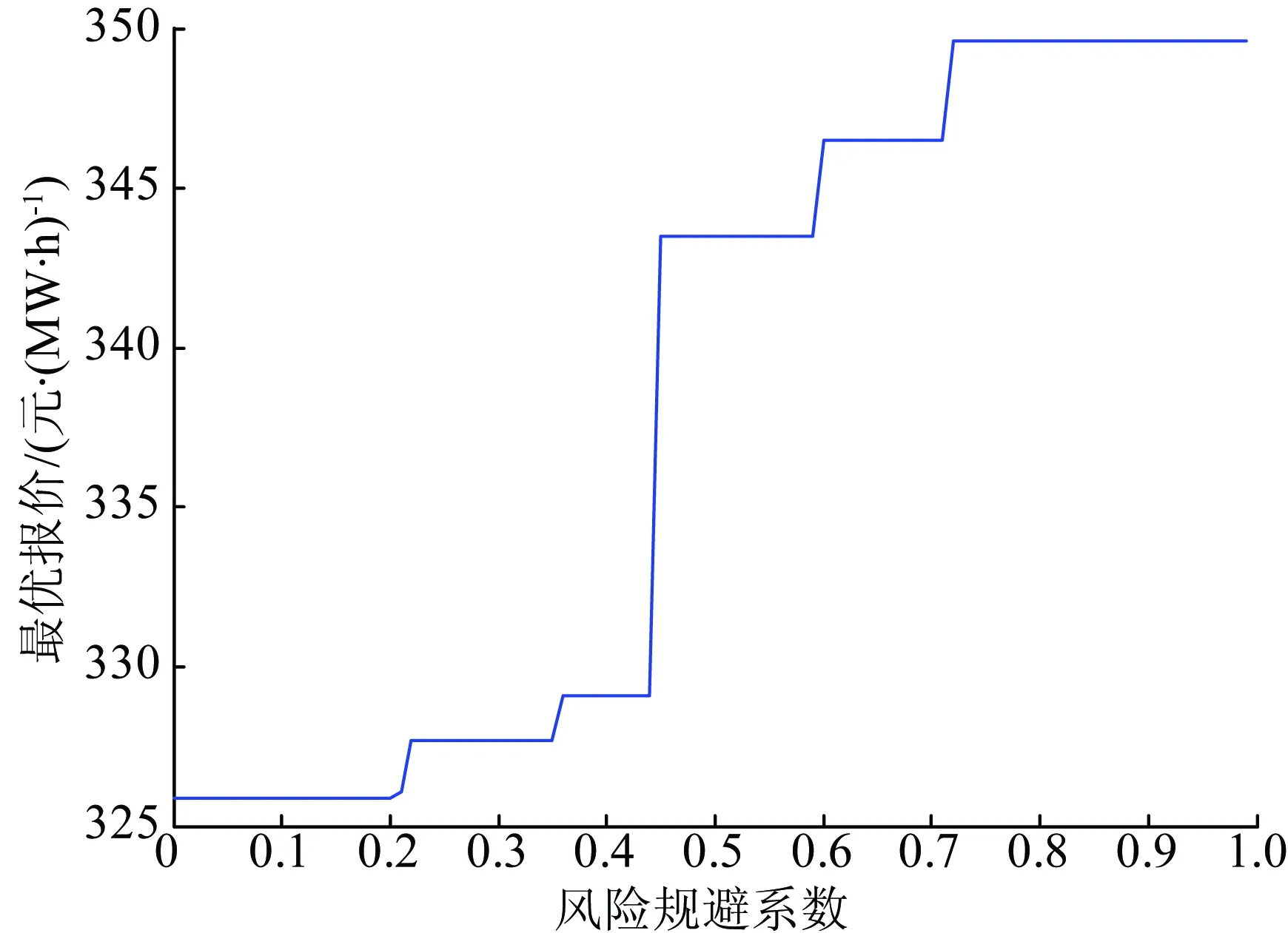
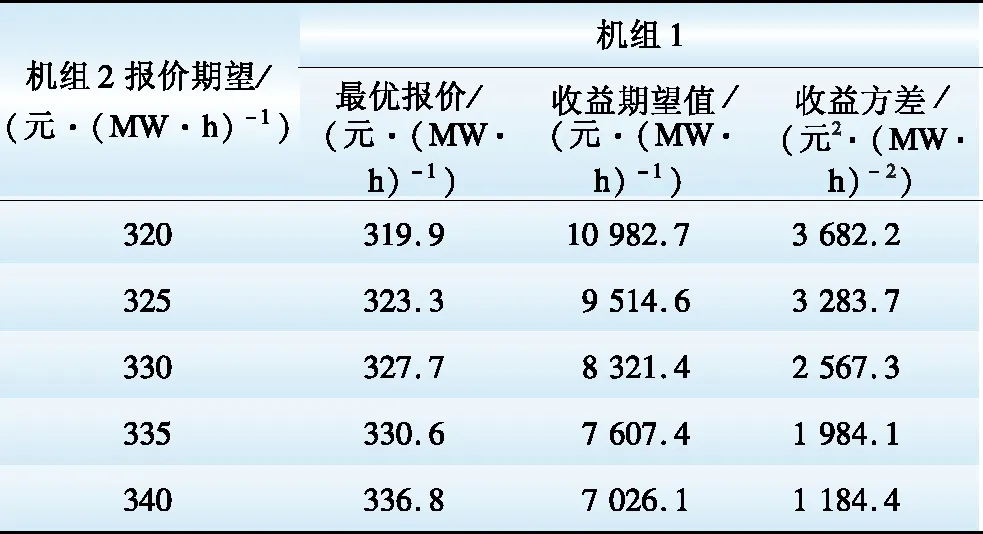
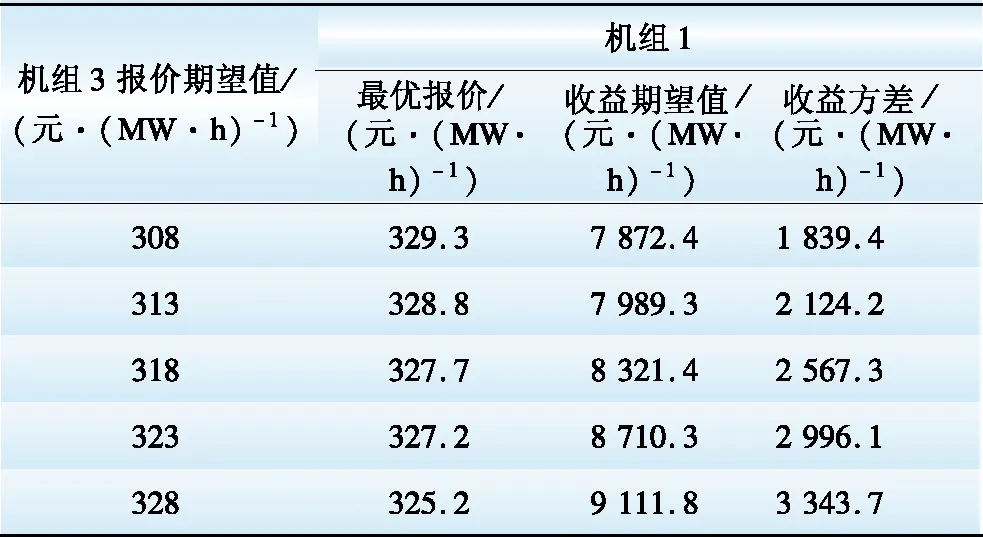
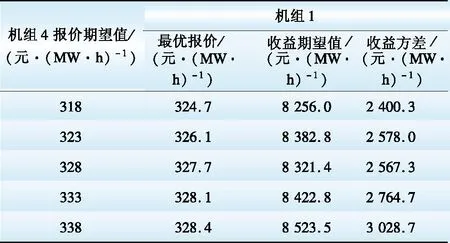
s.t. 0

(9)

同理，以第j台发电权受让机组为研究对象。在考虑受让方机组报价约束的情况下，最大化受让方机组j的预期收益问题可用下述优化模型描述：

(10)

s.t. Pbuy,j>Cbuy,j

(11)

采用预期收益的期望值构造发电权竞价策略在一定程度上考虑了发电权交易的风险。以发电权出让方机组i为例，当其试图通过不断降低自身报价以提高交易收益时，就可能导致无法匹配到发电权受让机组的风险，这可由期望收益降低反映出来。相似地，当出让方机组i试图通过提高自身报价以获得更多发电权交易量时，将面临每笔发电权交易收益值下降的风险，这也可由期望收益降低反映出来。

2.2 考虑收益波动风险的发电权竞价模型

2.1节给出的发电权交易最大化预期收益模型考虑了报价过高时可能出现的交易无法达成的风险，但未考虑各个竞价策略下的收益波动情况，即发电权交易的收益波动风险[6]。在2.1节模型的基础上，引入收益波动风险，用下式描述发电权竞价模型的优化目标：

max S=(1-λ)E(g)-λD(g)

(12)

式中：S表示综合收益指数，反映了期望交易收益及交易收益波动；λ(0≤λ<1)表示收益波动风险规避系数，反映参与发电权交易的机组对于收益波动风险的规避程度，λ越小则规避程度越低，λ=0表示机组完全不考虑交易的波动风险，等效于式(8)及式(10)的预期收益最大化模型；g为所研究机组的收益；E(g)和D(g)分别为参与发电权交易机组的收益期望值和方差。

式(12)同时适用于发电权出让和受让机组，只需将相应的收益期望值、收益方差和约束条件代入即可。

3 发电权交易竞价策略的方法与算法

3.1 高低匹配机制确定发电权交易量

在发电权交易市场中，成交量Qij是基于发电公司的报价由所采用的市场机制确定。可以采用多种不同的市场机制，相应的有不同的优化模型结构，包括社会福利最大化模型、效用最大化模型、能耗最优模型等[2]。这里针对采用高低匹配机制的发电权交易市场，采用社会福利最大化模型来确定发电权成交量，进而构造发电公司的竞价策略。需要指出，下述方法的思路对于其他优化模型结构同样适用。

社会福利最大化模型可描述为：

(13)

(14)

针对高低匹配机制，优先撮合社会福利最大的交易对，不断重复此过程直至交易量达到上限或剩余交易对的最大社会福利为负值。文献[15]详细介绍了高低匹配机制，在此不再赘述。

3.2 其他机组的报价分布函数

假定以发电权出让方机组i作为研究对象，则对于其他发电权出让机组和受让机组，需考虑其可能的报价。机组i不可能预先知道其他机组的报价，但可以根据其他机组的历史报价情况，估计其报价分布函数。令除出让方机组i以外所有发电权出让方、受让方机组报价集合为P=(Psell,1，Psell,2，…，Psell,i-1，Psell,i+1，…，Psell,n；Pbuy,1，Pbuy,2，…，Pbuy,m)，并假设其他机组的报价服从正态分布[19]，即

P～N(U,D)

(15)

式中：U和D分别为机组报价集合P的期望值向量和协方差矩阵，并可描述为：

U=[μsell,1,μsell,2,…,μsell,i-1,μsell,i+1,…,

μsell,n,μbuy,1,μbuy,2,…,μbuy,m]T

(16)

(17)

式中：μ和σ分别表示各机组的报价期望值与标准差；ρij表示机组i与机组j之间报价的相关系数。由于发电权参与方机组报价是独立进行的，可认为不同机组间的相关系数为0。但是，如果考虑2台或以上机组属于同一发电公司的情况，可根据实际情况设置相关系数。这里只讨论发电机组之间报价相互独立的情况，故令D矩阵为对角矩阵，即D矩阵的非对角元素均为0。

需要指出，所研究机组估计其他机组的报价分布函数时需要利用其他机组的历史报价数据。

3.3 蒙特卡洛法求解机组收益统计数据

在前文构造的考虑收益风险的发电权竞价模型中，需要求解所研究机组在发电权竞价市场中收益的期望值和方差。对于机组收益的统计数据，可采用蒙特卡洛仿真方法求解E(g)和D(g)的近似值。以发电权出让方机组i作为研究机组，任一次蒙特卡洛抽样仿真的具体实现过程如下：

(1)设定研究机组的报价Psell,i及其收益波动风险规避系数λ；

(2)根据其他发电权出让机组、受让机组的报价概率分布函数，抽样模拟报价情况；

(3)按照3.1节描述的高低匹配发电权成交量计算模型，计算该模拟报价情况下的发电权成交结果，并计算所研究机组的收益情况。

对于任一给定的报价情况，重复足够多次的蒙特卡洛模拟过程，就可以利用样本的无偏差估计量近似得到收益期望值和方差，即：

(18)

(19)

式中：g(t)表示第t次蒙特卡洛仿真得到的所研究机组的收益；N表示蒙特卡洛仿真次数。

对于任一报价情况，可以重复上述过程获得收益统计数据，进而利用式(12)求取综合收益指数S。

需要指出，蒙特卡洛仿真方法是通过大量抽样过程来模拟随机变量的概率分布，不同次抽样得到的计算结果一般相同。不过，只要抽样次数足够多，就可以将计算误差控制在可接受范围以内。

4 算例分析

4.1 算例数据

在图1所示的3节点电力系统中，假设共有5台发电机组参与月度发电权交易，机组1和2为发电权出让方，机组3、4和5为受让方。在月度发电权交易中机组申报该月内计划交易的发电权电量及相应的交易价格，由电力交易中心组织撮合匹配。以出让机组1作为研究对象，各机组参数及机组1对其他机组报价的概率分布函数的参数的估计值见表1。

表1 机组参数

Table 1 Parameters of generating units

位于节点A的机组的发电权出让给节点B或C的机组时有利于降低网损和缓解系统潮流负担。给定发电权交易的固定成本Cij,con(i=1,2；j=1,2,3)为0.5元/(MW·h)，针对系统典型潮流情况得到的地域成本矩阵Creg为

(20)

Creg的3行元素依次表示A、B、C节点的发电出让方机组与A、B、C节点的发电权受让方机组的交易地域成本。例如，Creg的第2行第3列元素表示节点B出让发电权给节点C的机组时的交易地域成本为1.5元/(MW·h)。基于发电权交易的固定成本及地域成本，可求得参与交易各方的交易成本见表2。

表2 发电权交易成本

Table 2 Costs of generation-right trade 元·( MW·h)-1

给定蒙特卡洛仿真次数为2 000。下面考察不同情形下的机组竞价策略。

4.2 给定风险规避系数λ时的最优竞价策略

给定出让方机组1在风险规避系数λ=0.3的情形下的综合收益指数的变化趋势如图2所示。为提高计算速度，开始时先用较大步长来初步确定最优竞价策略所在区间，然后提高计算精度确定最优报价。初步计算后得知，机组1的最优报价位于区间300～350 元/(MW·h)之内，进一步精确计算得到图2所示结果，此时最优报价为327.7元/(MW·h)，在该报价下综合收益指数为5 054.8，收益的期望值和方差分别为8 321.4 元/(MW·h)和2 567.3 元2/(MW·h)2。由于给定的风险规避系数较小(0.3)，从图3展示的机组收益期望与机组的报价变化趋势中可以看出，此时通过综合收益指数获得的机组最优报价接近通过收益期望值获得的最优报价。

图2 综合收益指数随报价变化趋势

图3 收益期望随报价变化趋势

4.3 给定不同风险规避系数λ时的最优竞价策略

给定不同的风险规避系数λ，出让方机组可以获得的收益也不同。保持其他机组的竞价策略不变，改变出让方机组1的风险规避系数，所求得的机组1的最优竞价策略和相应收益情况如表3、图4和图5所示。

从表3可看出，为保证有更大机会获得更多收益，减少波动风险，随着λ的增大，机组1的最优报价越来越高，相应的收益方差随之下降。这说明机组1利用λ调整了自身能够接受的报价风险水平，从而使得最终收益的波动性减小。从图4和图5可以看出，λ的改变对机组最优报价的影响呈现阶梯状，说明λ在给定水平下机组采取的最优报价是一致的。当λ较大时，虽然收益期望相比λ较小时有所降低，但相应的波动风险减小。对于发电权出让方机组1而言，在λ较大时更希望通过提高报价来增加自身发电权交易成功的可能性，以获取发电权交易收入。

表3 给定不同风险规避系数λ时的最优报价及相应收益

Table 3 Optimal bidding prices and profits under differentλvalues

图4 给定不同风险规避系数λ时的最优报价

图5 给定不同风险规避系数λ时的最优收益期望

4.4 其他机组报价对所研究机组最优竞价策略的影响

4.4.1 其他发电权出让方机组报价的影响

以出让方机组1作为研究机组，考察其竞争对象出让方机组2的报价对机组1的影响。假定出让方机组1的风险规避系数λ=0.3。改变机组2的报价期望值，其他机组的报价参数均保持不变，此时机组1的最优报价如表4所示。

表4 机组2报价变化对机组1最优报价的影响

Table 4 Impacts of different bidding prices of unit 2 on the optimal bidding price of unit 1

当机组2的报价提高时，为保持自身在发电权交易市场中的竞争力，机组1的最优报价水平也有所提高，且提价幅度与机组2的提价水平相当。由于发电权出让机组希望成交价格越低越好，所以不断提高报价水平会压缩出让机组的收益空间，导致收益的期望值下降。

4.4.2 发电权受让方机组报价的影响

仍然以出让方机组1作为研究对象，考察受让方机组的报价对机组1最优报价的影响。

保持其他机组的报价策略不变，改变机组3报价的期望值，此时机组1的最优报价见表5。

表5 受让方机组3报价变化对机组1最优报价的影响

Table 5 Impacts of different bidding prices of unit 3 on the optimal bidding price of unit 1

保持其他机组的报价策略不变，改变机组4报价的期望值，此时机组1的最优报价如表6所示。

表6 受让方机组4报价变化对机组1最优报价的影响

Table 6 Impacts of different bidding prices of unit 4 on the optimal bidding price of unit 1

由表5和表6可以看出：(1)当机组3的报价水平提高时，机组1的报价水平略有降低；(2)当机组4的报价水平提高时，机组1的报价水平略有提高。这是由于有多台发电权受让机组，当某台受让机组单方面提高自身机组报价时，出让机组可以与其他未提价受让机组撮合进行发电权交易，出让机组受到的影响相对较小。

5 结 论

针对采用高低匹配机制的集中竞价发电权交易模式，构建了发电机组的最优竞价策略优化模型，并采用蒙特卡洛仿真方法求解。算例计算结果表明，所提出的方法可以根据发电公司对风险的喜恶程度对收益与风险进行折中处理，针对其他机组报价策略变化给出相应的报价调整策略，进而获得计及风险约束的最优报价策略。

[1]林昶咏，文福拴，蒙文川，等．两部制电价机制下的发电权双边交易谈判模型[J]．电力建设，2016，37(3)：91-99． LIN Changyong，WEN Fushuan，MENG Wenchuan，et al．Generation-right bilateral transaction negotiation model based on two-part electricity price[J]．Electric Power Construction，2016，37(3)：91-99．

[2]尚金成．基于节能减排的发电权交易理论及应用：(一)发电权交易理论[J]．电力系统自动化，2009，33(12)：46-52． SHANG Jincheng．Generation right trade theory and its applications based on energy-saving and emission-reducing (part one)：Generation right trade theory[J]．Automation of Electric Power Systems，2009，33(12)：46-52．

[3]王雅娟，王先甲．一种激励相容的发电权交易双边拍卖机制[J]．电力系统自动化，2009，33(22)：25-28． WANG Yajuan，WANG Xianjia．An incentive compatible double auction mechanism of generation rights trade[J]．Automation of Electric Power Systems，2009，33(22)：25-28．

[4]肖健，文福拴．发电权交易的阻塞调度[J]．电力系统自动化，2008，32(18)：24-29． XIAO Jian，WEN Fushuan．Congestion dispatch for generation rights trade[J]．Automation of Electric Power Systems，2008，32(18)：24-29．

[5]吴杨，刘俊勇，高红均，等．基于风险决策的风火发电权交易研究[J]．电网技术，2016，40(3)：833-839． WU Yang，LIU Junyong，GAO Hongjun，et al．Research on power generation right trading between wind power and thermal power based on risky decision-making[J]．Power System Technology，2016，40(3)：833-839．

[6]马新顺，文福拴，倪以信，等．计及风险的发电公司最优竞价策略[J]．电力系统自动化，2003，27(20)：16-20． MA Xinshun，WEN Fushuan，NI Yixin，et al．Development of optimal bidding strategies for generation companies with risk management[J]．Automation of Electric Power Systems，2003，27(20)：16-20．

[7]马新顺，刘建新，文福拴，等．计及风险并考虑差价合约的发电公司竞价策略研究[J]．华北电力大学学报，2005，32(1)：37-41． MA Xinshun，LIU Jianxin，WEN Fushuan，et al．Development of risk-constrained optimal bidding strategies for generation companies in electricity markets with contract for difference[J]．Journal of North China Electric Power University，2005，32(1)：37-41．

[8]马新顺，文福拴，刘建新．构造发电公司最优竞价策略的机会约束规划方法[J]．电网技术，2005，29(10)：35-39． MA Xinshun，WEN Fushuan，LIU Jianxin．A chance constrained programming based approach for building optimal bidding strategies for generation companies with risk management[J]．Power System Technology，2005，29(10)：35-39．

[9]李士动，张孝君，张立柱，等．基于外部成本内置法的备用市场竞价模型[J]．电力建设，2016，37(3)：63-70． LI Shidong，ZHANG Xiaojun，ZHANG Lizhu，et al．A reserve market bidding model based on internalization of external cost[J]．Electric Power Construction，2016，37(3)：63-70．

[10]伍玉林，文福拴，丁剑鹰,等．发电公司在发电权交易市场的竞价策略初探[J]．电力系统自动化，2010，34(17)：6-11． WU Yulin，WEN Fushuan，DING Jianying，et al．A preliminary investigation on bidding strategies for generation companies in generation-right trading markets[J]．Automation of Electric Power Systems，2010，34(17)：6-11．

[11]宋艺航，唐晓瑭，张会娟，等．基于Zeuthen决策与贝叶斯学习的发电权双边交易模型[J]．电力系统自动化，2013，37(11)：51-57． SONG Yihang，TANG Xiaotang，ZHANG Huijuan，et al．A generation rights bilateral trade model based on Zeuthen strategy and Bayesian learning[J]．Automation of Electric Power Systems，2013，37(11)：51-57．

[12]夏清，孙正运．考虑交易成本的区域市场撮合交易模型[J]．电网技术，2005，29(17)：1-4． XIA Qing，SUN Zhengyun．Application of high-low match methods to regional electricity market considering transaction costs[J]．Power System Technology，2005，29(17)：1-4．

[13]于琪．区域发电权交易优化模式研究[D]．北京：华北电力大学，2012． YU Qi．Research on the regional generation rights trade optimization mode[D]．Beijing：North China Electric Power University，2012．

[14]王睿，张粒子，张丽娟，等．区域发电权交易模式研究[J]．华北电力大学学报，2012，39(4)：52-58． WANG Rui，ZHANG Lizi，ZHANG Lijuan，et al．Study on regional generation right exchange mode[J]．Journal of North China Electric Power University，2012，39(4)：52-58．

[15]黎灿兵，康重庆，夏清，等．发电权交易及其机理分析[J]．电力系统自动化，2003，27(6)：13-18． LI Canbin，KANG Chongqing，XIA Qing，et al．Generation rights trade and its mechanism[J]．Automation of Electric Power Systems，2003，27(6)：13-18．

[16]郑欣，蒋传文，李磊，等．基于能耗和效益最优的发电权节能降耗分析[J]．电力系统自动化，2008，32(24)：39-42． ZHENG Xin，JIANG Chuanwen，LI Lei，et al．Analysis of generation rights trade based on optimization of energy-saving and efficiency[J]．Automation of Electric Power Systems，2008，32(24)：39-42．

[17]王雁凌，程倩．基于节能降耗的发电权交易模型[J]．电力系统保护与控制，2010，38(18)：28-32． WANG Yanling，CHENG Qian．Generation rights trade model based on energy conservation[J]．Power System Protection and Control，2010，38(18)：28-32．

[18]王睿，张粒子，张丽娟，等．区域发电权交易模式研究[J]．华北电力大学学报，2012，39(4)：52-58． WANG Rui，ZHANG Lizi，ZHANG Lijuan，et al．Study on regional generation right exchange mode[J]．Journal of North China Electric Power University，2012，39(4)：52-58．

[19]李益国，沈炯，刘西陲．基于机会约束规划的发电公司竞标策略[J]．中国电机工程学报，2006，26(10)：120-123． LI Yiguo，SHEN Jiong，LIU Xichui．A new bidding strategy for power plants based on chance-constrained programming[J]．Proceedings of the CSEE，2006，26(10)：120-123．

(编辑 张媛媛)

Bidding Strategy for Generation Companies Participating in Generation-Right Trading Market Employing High-Low Matching Mechanism

MENG Wenchuan1, LIN Changyong2, WEN Fushuan2, WU Hongliang1, SONG Yihang1, ZHANG Xiang1

(1.State Key Laboratory of HVDC, Electric Power Research Institute, China Southern Power Grid, Guangzhou 510080, China; 2. School of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

Generation-right trade is an efficient approach for optimizing the power structure and promoting energy conservation and emission reduction, which is widely used in domestic power industry. The adopted bidding strategies of generation companies in the generation-right trading market could have significant impacts on their profits, which is an important issue for the generation companies. Under this background, this paper develops a risk-constrained optimal bidding strategy for generation companies based on the centrally bidding platform of generation-right trade market employing the high-low matching mechanism. Firstly, we construct the mathematical model to evaluate the costs and benefits for both sides participating in the generation-right trade. Then, we construct the optimization model of the risk-constrained optimal bidding strategy for generation companies participating in generating-right trading market based on the high-low matching mechanism, which can be solved by Monte Carlo simulation method. Finally, we adopt a numerical example to demonstrate the proposed optimal bidding strategy model and the presented method, and analyze the impacts of bidding behaviors of other power companies on the optimal bidding strategy of the studied power company.

generation-right trade; bidding strategy; high-low matching; Monte Carlo simulation

国家重点基础研究发展规划项目(973计划)(2013CB228202); 国家自然科学基金项目(51477151); 南方电网科学研究院科研项目 (CSGTRC-K153018)

TM 715； F 426.6

A

1000-7229(2016)11-0001-08

10.3969/j.issn.1000-7229.2016.11.001

2016-08-13

蒙文川(1976)，男，博士，高级工程师，主要从事电力网络规划、能源经济等方面的研究工作；

林昶咏(1992)，男，硕士研究生，主要从事电力经济与电力市场、智能电网等方面的研究工作；

文福拴(1965)，男，教授，博士生导师，本文通信作者，主要从事电力系统故障诊断与系统恢复、电力经济与电力市场、智能电网与电动汽车等方面的研究工作；

吴鸿亮(1981)，男，博士，高级经济师，主要从事电力经济领域研究工作；

宋艺航(1986)，男，博士，经济师，主要从事电力能源经济领域研究工作；

张翔(1988)，男，硕士，助理研究员，主要从事能源经济、电力系统规划领域研究工作。

Project supported by National Program on Key Basic Research Project (973 Program) (2013CB228202); National Natural Science Foundation of China (51477151)