基于STM32的六自由度平台的姿态测量系统设计
胡 雄, 汪 超, 唐 刚
(上海海事大学 物流工程学院, 上海 201306 )
基于STM32的六自由度平台的姿态测量系统设计
胡 雄, 汪 超, 唐 刚
(上海海事大学 物流工程学院, 上海 201306 )
提出一种新型的六自由度平台的姿态测量系统设计方案, 该方案是以STM32为主控制器实现对平台的数据采集和姿态计算. 由传感器得到平台的加速度、角速度和磁阻数据, 采用四元数法作为六自由度平台的姿态更新算法, 经互补滤波后得到六自由度平台的姿态角, 通过无线传输到上位机显示, 并将数据存于外接存储器中. 上位机显示结果和试验数据表明该六自由度平台姿态测量系统是稳定可靠的.
六自由度平台; STM32; 姿态测量; 无线传输
六自由度平台是由运动平台通过铰链连接6条伸缩杆的一端, 而伸缩杆的另一端通过铰链连接下方固定平台而构成的空间并联机构[1]. 六自由度平台在各种训练模拟器如舰艇模拟器、飞行模拟器中有着非常广泛的应用, 并在飞行器的空间对接模拟试验中发挥了重要的作用[2]. 对于试验设备的研究与其性能的检测, 六自由度平台提供了较为真实的试验环境.
随着船舶科技的不断进步, 船舶的安全性越来越受到人们的重视. 船舶在行驶过程中因为各种因素的影响会发生晃动, 如果船舶的姿态不能保证在一定的范围内, 就会对船舶的安全造成威胁. 船舶上电子设备的正常运行、船上人员的正常生活和船舶上手术的操作等问题都需要船舶保持其平稳性. 因此, 船舶在行驶中, 其姿态参数和稳定性有着至关重要的作用. 然而, 船舶的研制是一项浩大而复杂的工程, 直接用实体船进行试验, 尽管能获得最真实、最具说服力的姿态响应, 但试验成本过高, 并有着一定的危险性. 若利用计算机对船舶性能模拟仿真, 所建立的数学模型采用人为的方式推导而来, 得到的姿态响应数据很难有说服力. 六自由度平台的模拟仿真, 在实验室中将船舶在海洋中摇摆的姿态和运动模拟出来, 既能很好地接近实际情况, 又能避免大量的人力、物力资源的浪费. 这种半物理仿真的方法也是目前研究船舶姿态最为有效的方法.
六自由度平台的姿态测量是平台运行的关键技术之一, 实时得到六自由度平台的姿态数据并反馈给操作台, 从而更好地控制六自由度平台的模拟运转操作. 本文采用STM32F103RBT6为主控芯片, 由MPU6050六轴传感器和HMC5883L三轴数字罗盘完成六自由度平台的数据采集, 并经过数据处理和整合后得到其姿态角数据, 并将角速度、加速度等数据存储于外接存储器K9K8G08U0M中, 通过无线传输到上位机, 在PC端实现六自由度平台的姿态信息显示.
1 六自由度平台的工作原理
六自由度平台工作时, 它通过6条伸缩杆的伸缩运动来改变伸缩杆的杆长, 从而使得上平台呈现不同的空间姿态, 实现上平台在空间中六自由度的运动, 分别为升降、横移、纵摆、俯仰、滚转、偏航, 即为x、y、z轴方向的平移和绕x、y、z轴的旋转运动, 或者是这些运动的复合运动[1-2]. 六自由度平台的三维模型如图1所示.

图1 六自由度平台的三维模型Fig.1 Three-dimensional model of six degrees of freedom platform
2 六自由度平台的姿态测量系统设计
2.1 姿态测量系统框架设计
姿态测量的方法是六自由度平台姿态测量系统的核心, 常见的测量方法有加速度计和陀螺仪组合进行测量的惯性组合测量法、电子罗盘测姿方法、GPS姿态算法、图像视觉处理法等[3]. GPS姿态算法主要应用于视野开阔、障碍物较少的室外场所, 如飞机和船舶的姿态测量, 不适合于室内测量[4]. 图像视觉处理法在医疗和工业上的应用较为广泛, 但是其测量系统体积较大, 成本昂贵, 姿态解算方法较为复杂. 加速度计和磁场力计的测量方法有着体积小、测量速度快、成本低等优点, 但在动态测量时数据准确度不够. 陀螺仪单独测量姿态时, 在测量角度时存在漂移问题[5].
结合上述各测量方法的优缺点, 本文采用三轴加速度计、三轴陀螺仪、三轴磁阻传感器作为传感器单元, 其中, 三轴加速度计和三轴陀螺仪采用集成的MPU6050六轴传感器, 三轴磁阻传感器采用HMC5883L数字罗盘. 姿态测量装置实物如图2所示. 由四元数姿态算法得到六自由度平台的姿态角数据, 为了解决姿态测量系统中加速度计和磁阻传感器在使用中受线性加速度干扰和磁场干扰问题, 以及陀螺仪在四元数法中的累积误差问题, 系统设计相应的互补滤波算法对传感器信息进行融合, 从而解出六自由度平台的姿态, 最后将姿态数据和传感器数据通过无线传输, 在PC端上位机上进行显示, 同时将传感器信息和姿态信息存储于存储单元里. 姿态测量系统的设计方案如图3所示.
2.2 姿态更新算法
姿态更新算法是姿态测量系统的核心, 只有确定姿态更新算法, 才能设计相应的滤波算法来估计六自由度平台的全姿态选择的姿态更新算法是否合适, 将会直接影响六自由度平台姿态的测量结果. 欧拉角法、方向余弦法和四元数法是目前较为典型的姿态更新算法[6].
欧拉角法求解姿态角时, 不仅求解速度较为缓慢, 姿态求解方程中会出现“奇点”, 而且其最大的缺点在于并不能进行全姿态解算. 方向余弦法则是在求解过程中计算量过大, 不能快速地得到姿态结果, 因此很难达到实际工作中的目标. 四元数法不仅求解方程无奇性, 而且线性程度高, 方程解算的时间大大减少, 因此,本文姿态测量系统中选用四元数法作为姿态更新算法[7].

图2 姿态测量装置Fig.2 Attitude measurement device

图3 姿态测量系统设计方案Fig.3 Design program of attitude measurement system
四元数法求解姿态时所用的定位参数只有4个, 并且4个定位参数之间只有一个约束方程, 可以表示为一个1个标量部分和3个矢量部分组成的形式, 同样可以看作是由1个标量和1个矢量之和的形式. 实际工程中多采用特征四元数, 其标量部分可以看做一个坐标系相对于另一坐标系转角的一半的余弦值, 矢量部分可以看做某一时刻转动轴n的方向. 如式(1)中的R为一矢量, 相对于某一坐标系旋转了θ后得到新矢量R′, 在这里采用Rodrigue-Hamilton参数作为四元数实元,λ为其标量部分,p1、p2、p3为其矢量部分[7].
R′=qRq-1
(1)
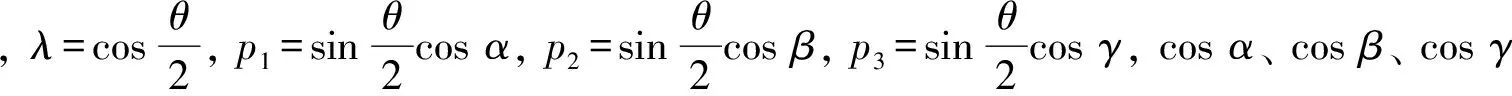
从上述方程中可以看出, 四元数法求解载体的姿态角时, 只需要求解4个一阶微分方程即可, 相比于方向余弦法, 其大大地减少了计算量, 能够满足工程中的实时性要求, 被广泛应用于捷联式惯性导航技术和空间技术中[8].
四元数法求解六自由度平台的姿态过程如下:
(1) 输入四元数方程在求解过程中初始姿态角, 如式(2)所示.
(2)

(3)

(4)
故姿态矩阵可以表示为
(5)
(4) 解算六自由度平台的姿态角, 得到θ、ψ、γ. 输入分别为T11(n)、T12(n)、T13(n)、T23(n)、T33(n), 利用方向余弦矩阵中对应项相等即可得到姿态角, 计算式如式(6)所示.
(6)
2.3 互补滤波算法
在实际使用中, 加速度传感器和磁阻传感器解算得到的姿态数据不会产生累积误差, 但是在运动加速度干扰和磁场干扰等情况下, 在短时间内姿态数据的精度较差. 陀螺仪的动态响应较好, 但是在计算姿态过程中会出现数据累积误差, 导致得到的结果没用使用价值. 因此,六自由度平台姿态测量系统中采用相应的互补滤波算法对传感器信息进行融合[9].

(7)
其中:A(s)+B(s)=1,A(s)=K/(S+K),B(s)=S/(S+K),S、K分别为磁阻传感器和加速度传感
器解算得到的姿态角度和陀螺仪解算得到姿态角度的权重值.A(s)具有低通滤波性,B(s)具有高通滤波特性, 从而分别将θjc中的高频噪声和ωm中的低频噪声滤除, 代入式(7)中可得:
(8)
式(8)的时域形式为
(9)
互补滤波算法中仅需要调节相应的K值即可, 系统的截止频率fc与K的关系满足:
(10)
其中:ts为系统的采样周期.
2.4 姿态测量系统的硬件设计
本文六自由度平台姿态测量系统的主控芯片选用STM32F103RBT6, 它是一款成本低、功耗低、性能高的cortex-M3架构内核的32位处理器产品, 满足该系统的性能需求. 加速度和角速度测量采用MPU6050六轴传感器, 相对于传统的多组件测量方法, 该传感器消除了加速度计与陀螺仪之间的轴差问题, 其不仅体积小, 且有自带的数字运动处理器, 较为方便地实现姿态解算, MPU6050传感器与主控芯片的接口方式如图4所示[10].
三轴数字罗盘选用HMC5883L, 用来测量六自由度平台的外界干扰磁场强度和地球磁场强度, 其采用了AMR(anisotropic magneto-resistance)技术, 有着轴向的高灵敏性和线性高精度性, 体积小且成本低, 满足本文姿态测量系统的性能需求, 数字罗盘与主控芯片的接口图如图5所示[11]. 数据存储模块采用三星公司的K9K8G08U0M, 该存储器有着1 GByte的存储空间, 它具有寻址简单、可靠性强、功耗低等特点, 由于采用NAND(Not AND)结构, 同时具有较强的抗震能力, 而且能保证10 a的数据存储时间.

图5 数字罗盘与主控芯片接口图Fig.5 Interface figure of digital compass and main control chip
无线传输模块选用nRF24L01+芯片, 该芯片工作频率为2.4~2.5 GHz, 具备自动重发功能和6个数据传输通道, 最大无线传输速率为2 Mbit/s, 它在通信率较高的设备互联间有着很好的效果, 具有功耗低、成本低、体积小等优点[12]. 六自由度平台的姿态测量系统的主控芯片STM32作为无线传输的发送端, 接收端也同样采用STM32芯片. 接收端通过无线传输得到传感器数据和姿态角数据, 通过USB将数据传输给PC端的上位机, 并在上位机上显示. 无线传输的示意如图6所示.
图6 无线传输示意图
Fig.6 Schematic diagram of wireless transmission
2.5 姿态测量系统软件设计
六自由度平台姿态测量系统的软件设计是整个系统中的重要组成部分, 它主要是下位机软件和上位机软件两个部分. 其中: 下位机主要包括系统的微处理器的初始化、传感器数据的采集和融合、姿态解算, 并将传感器信息和姿态解算结果发送给上位机; 上位机则是对下位机传输信息的解析, 并在显示界面上显示六自由度平台的姿态信息. 六自由度平台姿态测量系统的软件结构框图如图7所示.
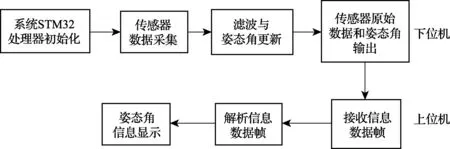
图7 系统软件结构框图Fig.7 Block diagram of the system software
2.6 上位机数据显示
PC端上位机通过USB传输得到传感器数据和姿态角信息, 并编写程序实现姿态测量模块运动姿态的模拟和显示. 图8和9分别为上位机显示的姿态变化时的三维模型和姿态欧拉角以及传感器原始数据的波形图, 可以很直接明了地看出平台的姿态, 在上位机中可以用相应的控件分析其角速度、加速度、磁通量波形图, 可直接放大波形图和改变其时间栅格. 上位机接收数据的格式为“$×1×2×3×4×5×6×7×8×9×10×11×12$”, 总共传输12个数据, 分别为三轴角速度、三轴加速度、三轴磁通量、三个姿态角.
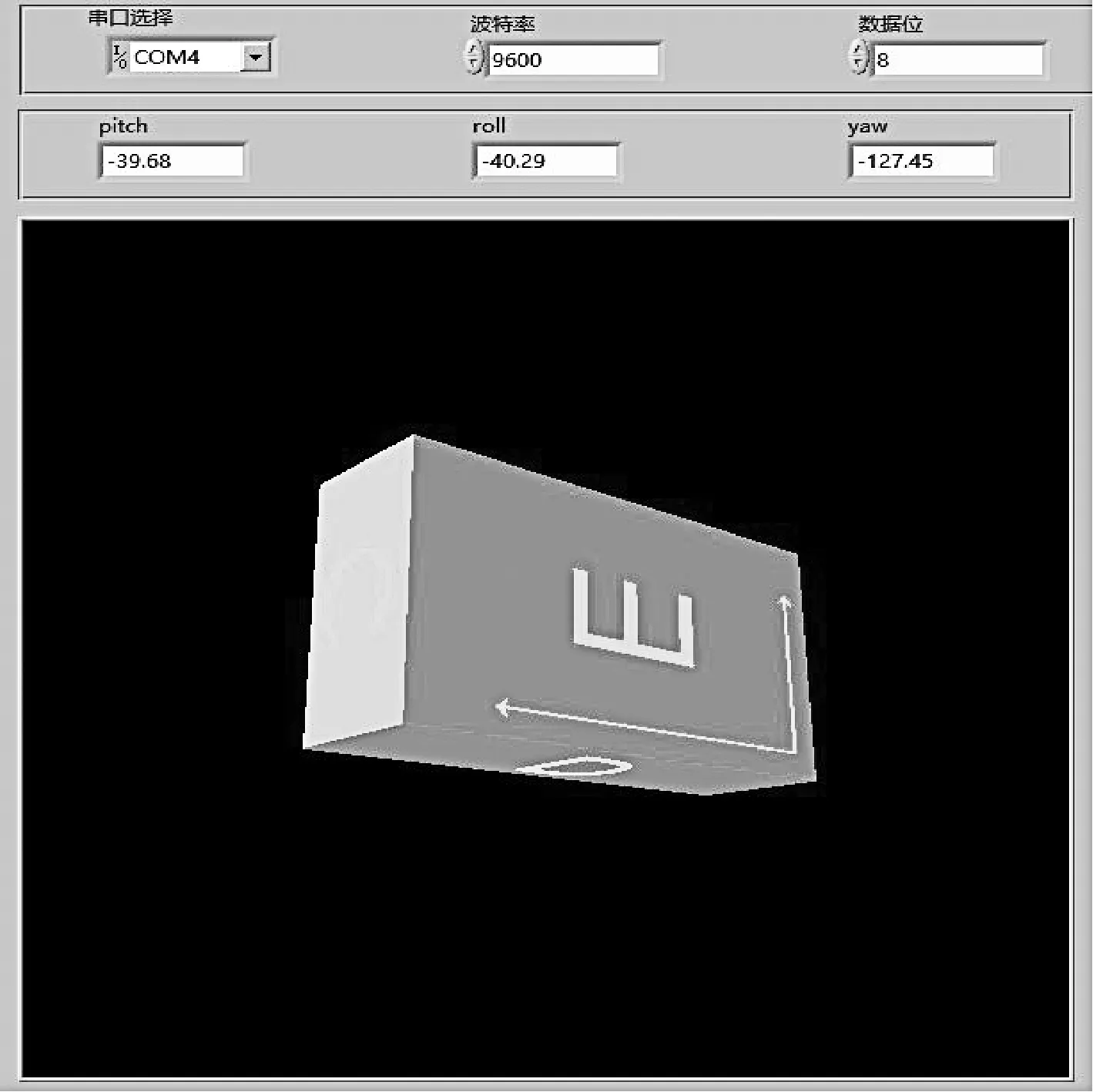
图8 三维模型和姿态角显示Fig.8 Three-dimensional model and attitude angle display
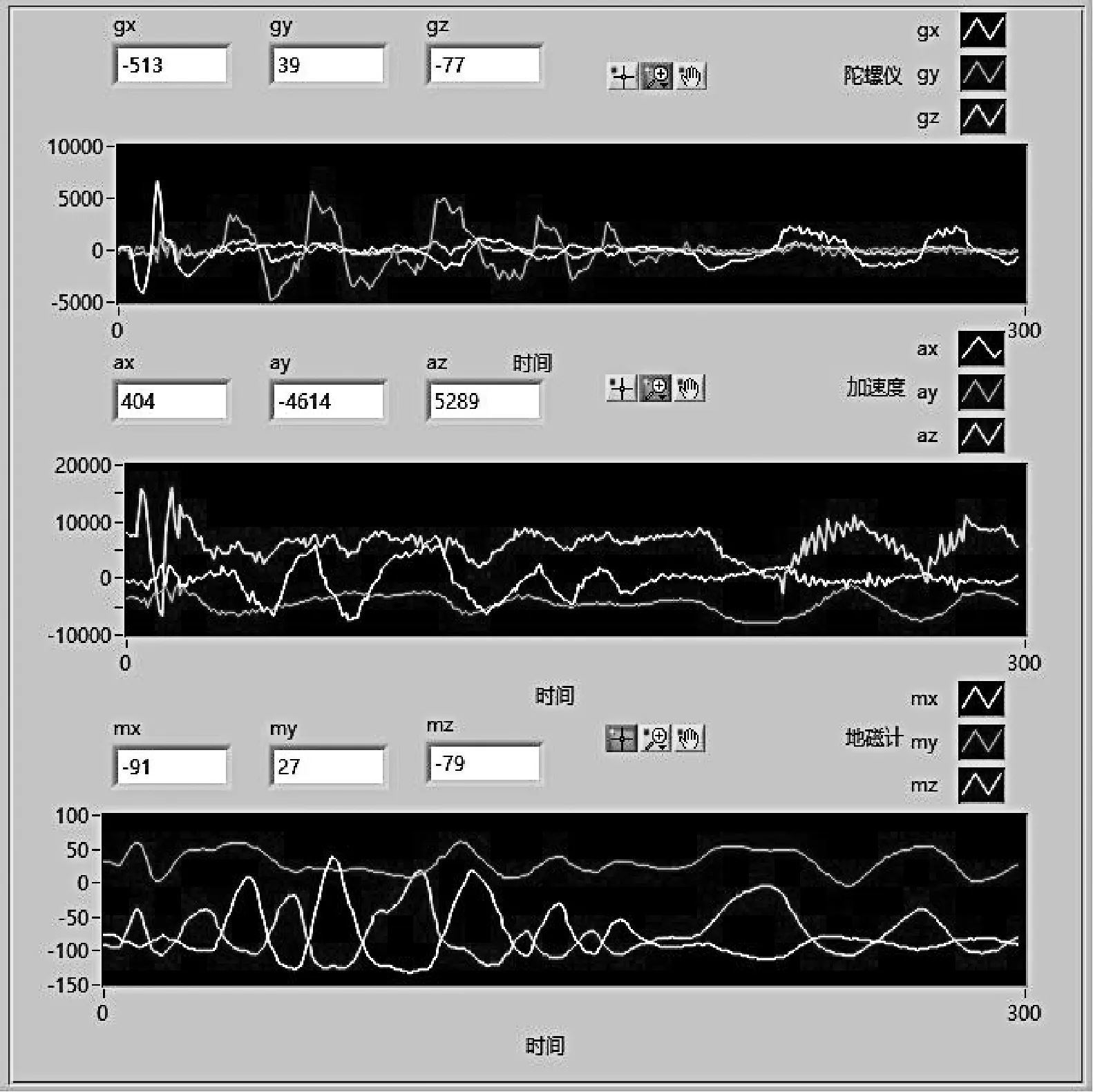
图9 传感器原始数据波形图Fig.9 Original data waveform figure of sensor
2.7 系统测试
为了测试六自由度平台姿态测量系统的性能, 进行了系统姿态测量精度试验. 将本文设计的姿态测量装置与标准的姿态测量装置进行姿态测量对比, 保持试验台上两者的重心在同一位置, 以标准的姿态测量装置为准, 记录所设计的姿态测量系统的数据, 取其3次平均值来代表姿态测量系统的精度.
试验中保证两个姿态测量装置的三轴平行, 将本文设计的姿态测量系统的实际数据与标准姿态测量装置得到的数值进行对比, 评价姿态角的测量精度, 俯仰角、滚转角、偏航角的测量结果如表1~3所示. 由表1~3可以看到, 俯仰角的绝对误差在0.10°以内, 滚转角的绝对误差在0.15°以内, 偏航角的绝对误差在0.18°以内. 由此可知, 本文所设计的系统能够很好地应用于六自由度平台的姿态测量.
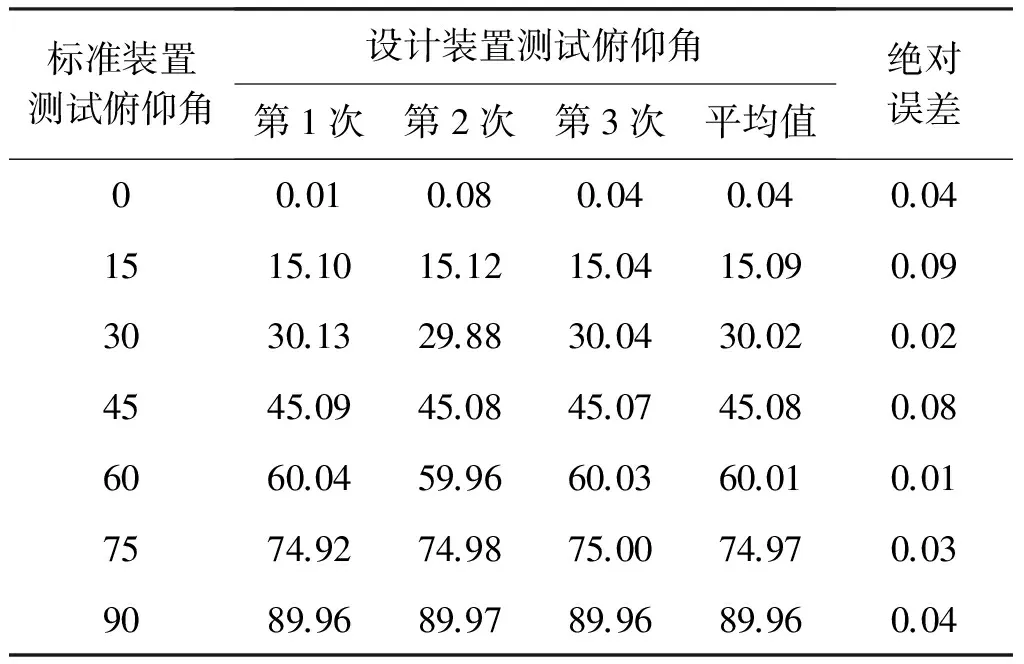
表1 俯仰角测量结果
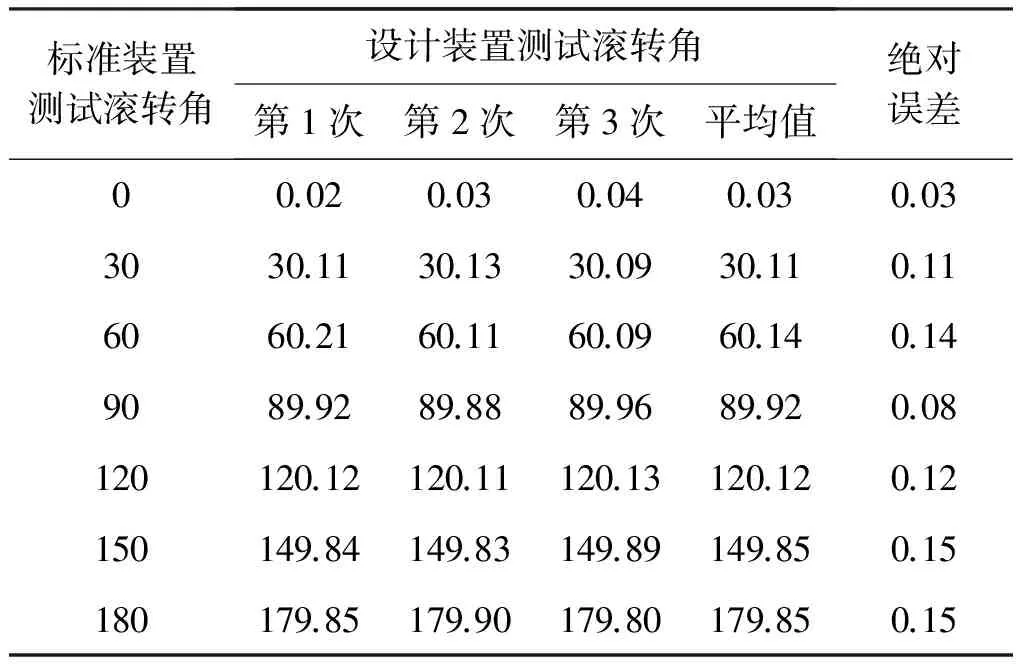
表2 滚转角测量结果

表3 偏航角测量结果
3 结 语
本文所设计的一种基于STM32的六自由度平台的测量系统, 采用了MPU6050六轴传感器与三轴数字罗盘的姿态测量模块, 四元数更新姿态, 互补滤波法提高姿态测量系统的精度. 该姿态测量装置体积小、易携带、成本低, 并且有着较高的精度. 试验测量数据基本稳定, 表明该姿态测量系统有着较好的性能和稳定性, 可以用于六自由度平台进行船舶模拟试验时的姿态测量, 为船舶的安全性提供了一定的保障.
[1] STEWART D A. Platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical, 1965, 180: 371-386.
[2] 杨世祥, 杨涛, 徐悦桐. 大型数字式六自由度运动平台的开发[J]. 液压与气动, 2003(8): 46-47.
[3] 朱荣, 周兆英. 基于MEMS的姿态测量系统[J]. 测控技术, 2002, 21(10): 6-9.
[4] 赵鑫炉. 基于MARG传感器的车辆姿态测量系统设计[D]. 太原: 中北大学仪器与电子学院, 2014.
[5] 朱文杰, 王广龙, 高凤岐, 等. 基于MIMU和磁强计的在线实时定姿方法[J]. 传感技术学报, 2013,26(4): 536-540.
[6] 刘建业, 曾庆化, 赵伟, 等. 导航系统理论与应用[M]. 西安: 西北工业大学出版社, 2009: 297-310.
[7] 张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16(10): 1964-1968.
[8] 胡淑娥. 关于四元数矩阵若干问题的结果与应用[D]. 长沙: 国防科学技术大学理学院, 2005.
[9] 郭晓鸿, 杨忠, 陈酷, 等. EKF和互补滤波器在飞行姿态确定中的应用[J]. 传感器与微系统, 2011, 30(11): 149-152.
[10] 傅忠云, 朱海霞, 孙金秋, 等. 基于惯性传感器MPU6050的滤波算法研究[J]. 压电与声光, 2015, 37(5): 822-825.
[11] 朱文杰, 王广龙, 高凤岐, 等. 基于MIMU和磁强计的在线实时定姿方法[J]. 传感技术学报, 2013, 26(4): 536-540.
[12] 谢辉程, 郭莉. 基于STM32的无线环境监控系统设计[J]. 软件, 2014, 35(12): 5-7.
A Six Degrees of Freedom Platform Attitude Measurement System Design Based on STM32
HUXiong,WANGChao,TANGGang
(School of Logistics Engineering, Shanghai Maritime University, Shanghai 201306, China)
A new type of attitude measuring system design scheme of six degrees of freedom platform is proposed, realizing data collection and attitude calculation for the platform using STM32 as the main controller. The acceleration, angular velocity and magnetic resistance data are obtained by the sensor, the quaternion method is adopted as the attitude updating algorithm of the six degrees of freedom platform, and the attitude angle of the six degrees of freedom platform can be got after the complementary filter, through the wireless transmission , the attitude angle is displayed on PC, also, the data is stored in external memory. The results and experimental data of the PC display show that the proposed six degrees of freedom platform attitude measuring system is stable and reliable.
six degrees of freedom platform; STM32; attitude measurement; wireless transmission
1671-0444 (2016)04-0597-07
2015-12-30
胡 雄(1962—),男,上海人,教授,博士,研究方向为机械工程.E-mail:huxiong@shmtu.edu.cn
V 19
A

