3-RRP平面并联机构的工作空间和灵巧度分析
刘小娟,李 虹,李瑞琴,郝亮亮,汪 辉
(中北大学 机械与动力工程学院,山西 太原 030051)
3-RRP平面并联机构的工作空间和灵巧度分析
刘小娟,李 虹,李瑞琴,郝亮亮,汪 辉
(中北大学 机械与动力工程学院,山西 太原 030051)
建立了3-RRP平面并联机构的正反解方程,利用Matlab/Simulink中的SimMechanics功能模块建立3-RRP平面并联机构以及其结构框图.采用滑杆的行程限制条件编程得出了3-RRP平面并联机构的工作空间范围.利用条件数转化到其倒数来对3-RRP并联机构进行灵巧度分析,得出了该机构的灵巧度的分布等高线,灵巧度在整个工作空间分布均匀,验证了该机构的运动学处于各向同性,各项性能也较好,研究结果为3-RRP平面并联机构优化设计和动力学研究等奠定理论基础.
Matlab;并联机构;工作空间;灵巧度
三自由度平面并联机构是平面并联机构研究较多的类型之一[1-2],近年来吸引了众多学者对其进行研究与开发.文献[3]运用BP神经网络建立适合3-RRP平面并联机构的神经网络模型,并求解出该机构的位置正解.文献[4]用平面3-PPR并联机构的位置逆解以及该机构的杆长等限制因素,采用Matlab编程得出其工作空间.文献[5]提出3-PRR并联机构获得最大区域没有奇异点的图形算法.文献[6]利用可操作数和条件数对3-RRR并联机构进行了灵巧度分析,得出该机构的灵巧性特点.文献[7]用几何方法建立平面三自由度并联机构工作空间与结构参数的关系,提出机构满足运动可能性的条件.
目前,国内外对3-RRP并联机构的运动学分析、动力学及仿真有一定的研究,而工作空间[8]和灵巧度是并联机构性能的重要指标,机构的灵巧度是描述一个机构运动失真程度及远离奇异点的程度,需对该机构灵巧度进行分析研究,以改善机构的运动性能.本文运用Matlab/Simulink中的SimMec-hanics功能模块建立3-RRP并联机构,对3-RRP并联机构的工作空间进行了仿真,以利用条件数对3-RRP并联机构进行了灵巧度分析,为此构型的特性研究及优化设计提供理论基础.
1 3-RRP并联机构描述及位置分析
3-RRP平面并联机构的机构简图如图1所示. 该机构可以实现2个平移和1个转动,由静平台、动平台和3个完全对称分布的运动支链组成,每条支链都是由2个转动副和1个移动副组成,移动副为末端支链与动平台相连.

图1 3-RRP并联机构简图Fig.1 Diagram of 3-RRP parallel mechanism
如图1所示,建立局部坐标系Bi-xiyi, △B1B2B3为正三角形,建立动坐标系p-xy,动坐标系固接在动平台上,随着动平台的运动而运动,中心点p处坐标值为(xp,yp,αp),其中,xp和yp分别为动坐标系在定坐标系中沿x轴和y轴方向上的位置坐标,αp为动坐标系在定坐标系的转动角度.设定转动副的初始转角为α1,α2,α3,3条支链中驱动杆BiCi的长度为H,连接杆CiDi的长度为L,三角形动平台外接圆半径为e,定平台B1B2B3的外接圆半径为R.
1.1 求解3-RRP并联机构位置正解
已知各驱动输入参数(θ1,θ2,θ3)的大小,求解动平台输出位姿参数(xp,yp,αp).建立如式(1)和(2)所示的位移方程:
H[cos(αi+αp)-cosαi]+L[sinαi-sin(θi+
αi)]+esinαi=xp+cisin(αi+αp)
(1)
H[sinαi-sin(αi+αp)]-L[cos(θi+ai)-
cosαi]+ecosαi=yp-cicos(αi+αp)
(2)
消去式中ci(ci为位移变量),整理化简为如式(3)所示的运动方程:
Eixp+Fiyp+Gi=0
(3)
式中:Ei=cos (αi+αp),Fi=sin (ai+αp),Gi=H(cosαp-1)+Lsin (θi-αp)+(L+e)sinαp.
根据机构的几何关系:
E1+E2+E3=0
(4)
F1+F2+F3=0
(5)
G1+G2+G3=0
(6)
将式(4)~(6)代入式(3)得到:
(7)
式中:u=3(L+e)-L(cosθ1+cosθ2+cosθ3),v=3H+L(sinθ1+sinθ2+sinθ3),w=3H.
求得的位置角αp代入式(1)和(2)中,求解得:
xp=sinαp[2Lsin(θ2-αp)+(L+e)sinαp+
H(cosαp-1)-Lsin(θ1-αp)]-
Lsin(θ1-αp)cosαp-(L+e)sinαp-
H(cosαp-1)
(8)
yp=cosαp[-2Lsin(θ2-αp)-3(L+e)sinαp-
3H(cosαp-1)-Lsin(θ1-αp)]-
Lsin(θ1-αp)sinαp-(L+e)sinαp-
H(cosαp-1)
(9)
式(7)~(9)联立就可得出3-RRP平面并联机构的位置正解.
1.2 求解3-RRP并联机构位置反解
求解并联机构的位置逆解,就是已知该机构动平台运动位置参数(xp,yp,αp),求解3个连杆的转动输入角参数(θ1,θ2,θ3).根据式(1)和(2)化简整理后得到运动学反解方程为
Risinθi+Sicosθi-Ti=0
(10)
式中:Ri=Lcosαp,Si=sinαp,Ti=H(1-cosαp)-cos (αp+αi)xp-sin (αp+αi)yp-(L+e)sinαp.
化简可得:
(11)
2 3-RRP并联机构工作空间分析
已知3-RRP平面并联机构参数:L=160 mm,H=80 mm,R=316 mm.本文求解图1所示的3-RRP并联机构工作空间:即在满足杆长尺寸范围的条件下,求解动平台中心点p可达空间点的集合.
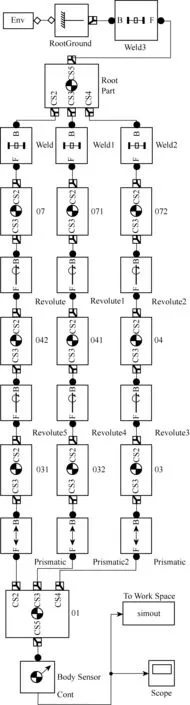
图2 3-RRP并联机构SimMechanics仿真模型Fig.2 SimMechanics simulation model of 3-RRP parallel mechanism
2.1 构建SimMechanics模型
在Matlab/Simulink工具箱建立并联机构模拟框图的步骤:(1) 确定刚体的惯性量、自由度、约束;(2) 建立检测和驱动模块组;(3) 以系统的运动形式和驱动力开始模拟;(4) 在SimMechanics窗口显示模拟结果.
根据3-RRP平面并联机构的参数,结合正反解的方程,建立平面3-RRP并联机构的模拟框图和机构简图,如图2和3所示.
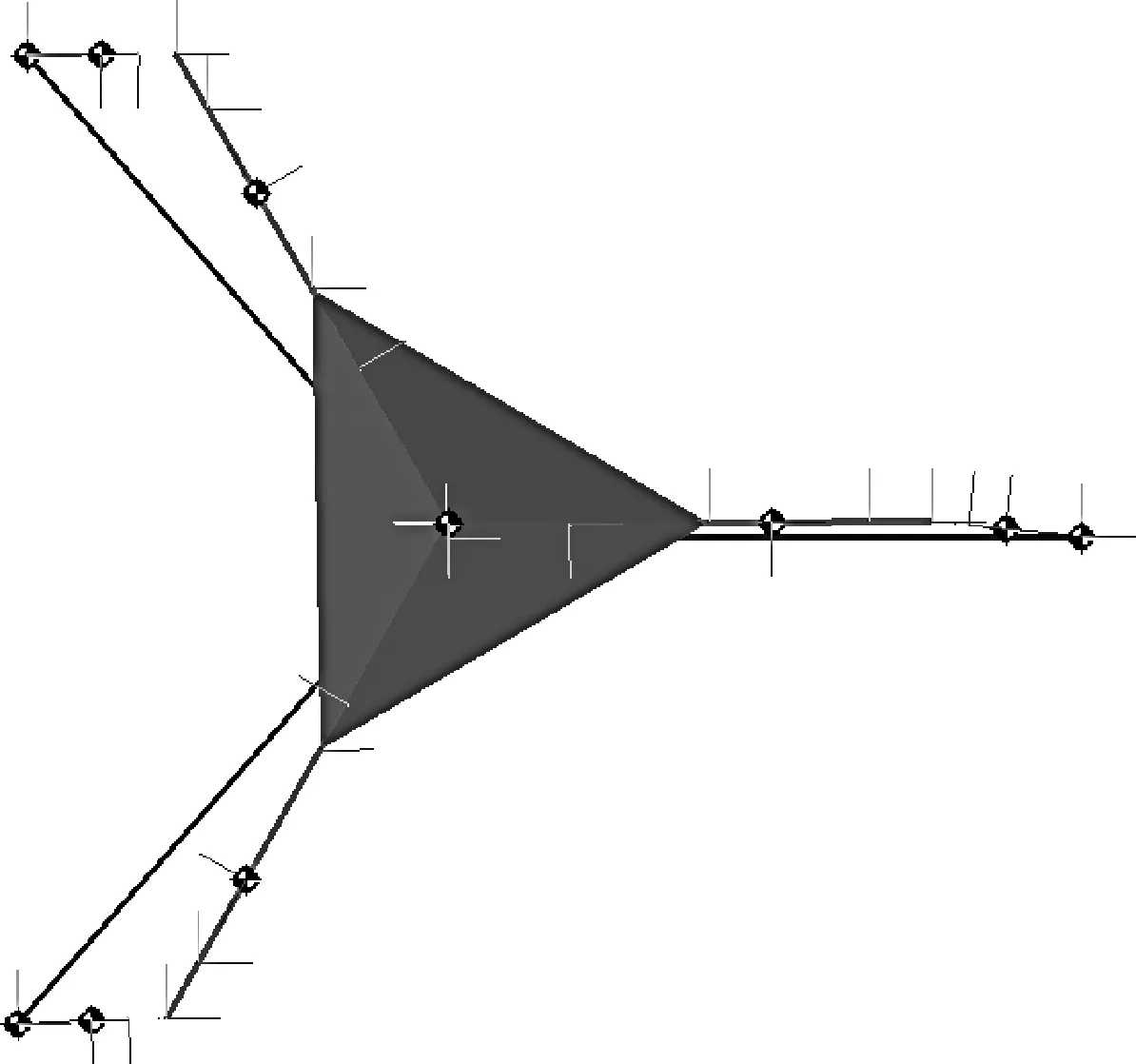
图3 3-RRP并联机构简图Fig.3 Diagram of 3-RRP parallel mechanism
由图2可知,RootPart为静定平台,由无自由度Weld模块连接到RootGround模块;机构的工作环境模块Env设置重力加速度向量和容许误差等;机构的旋转矩阵、刚体位置、速度(或角速度)和加速度(或角加速度)由刚体传感器Body Sensor模块测量. 机构3个轴向上的位置数据由传感器采集,再经过To Work Space模块传递到Matlab工作空间中并为用户查看及使用.
图3中的机构简图与图1中的是一致的,从而验证了用Matlab/Simulink建模的正确性.
2.2 求解3-RRP工作空间
设定滑杆杆长L变化范围为50~70 mm,利用Matlab可求得3-RRP的工作空间,如图4所示.

图4 3-RRP并联机构工作空间Fig.4 Working space of 3-RRP parallel mechanism
由于驱动副支链的惯性矩存在,使得该支链的运动产生偏离,故该3-RRP平面并联机构的工作空间也绕x轴产生了偏差Δx. 但是从图4可看出, 该机构的工作空间仍呈现对称性,在整个工作空间内结构紧凑,无空洞,说明该机构具有良好的工作性能.
3 3-RRP并联机构的灵巧度分析
定义条件数为
(12)
式中:‖*‖为任意矩阵的Euclide(欧几米德)范数.奇异值和条件数之间的相互关系[9]为
k(J)=σmax/σmin
(13)
式中:σmax为最大奇异值;σmin为最小奇异值.矩阵的条件数k取值范围为1~∞,本文根据该机构的雅克比矩阵可求得线速度和角速度的传递矩阵表示为Jv和Jw,求得线速度条件数k(Jv)和角速度条件数k(Jw)分别为
(14)
式中:σmaxv和σminv分别表示线速度传递矩阵Jv的最大奇异值和最小奇异值;σmaxw和σminw分别表示角速度传递矩阵Jw的最大奇异值和最小奇异值;1≤k(Jv)≤∞;1≤k(Jw)≤∞.由于k(Jv)和k(Jw)的变化范围较大,将条件数的倒数作为速度传递评价指标[10],如式(15)所示.
(15)
式中:c为机构的雅克比矩阵条件数的倒数.由此可知,c值越接近1,机构的输出偏差就越小,机构的各项性能也较好,并且此时机构运动学处于各向同性.
3-RRP平面并联机构的c分布如图5所示.由图5可知:c截面的变化值从外到内逐渐减小,c最大值和最小值分别为0.8和0.3;c在整个工作空间较均匀分布且由中心向四周逐渐减小,c值在工作空间的中心处接近1,则该机构的输出偏差较小,此时机构的各项性能也最佳,机构运动学处于各向同性.

图5 3-RRP并联机构的c分布图Fig.5 c distribution of 3-RRP parallel mechanism
4 结 论
(1) 本文建立了3-RRP平面并联机构的正反解方程.
(2) 利用Matlab构建3-RRP平面并联机构的SimMechanics模型与机构模型一致,说明Matlab/ Simulink建模的正确性.结合正反解的方程及特定参数,经Matlab编程求得3-RRP平面并联机构的工作空间,在整个工作空间内该机构结构紧凑且无空洞,说明该机构具有良好的工作性能.用本文方法求解机构工作空间,克服了利用极限理论编程运算的复杂,对高冗余度的机构工作空间求解优势更明显.
(3) 以机构的雅克比矩阵条件数的倒数作为速度传递评价指标,绘制了3-RRP并联机构的c分布图.在工作空间的中心处c的值接近1,此时机构运动学处于各向同性,各项性能最佳,为该机构特性研究及优化设计提供理论基础.
[1] ZEIN M, WENGER P, CHABLAT D. Non-singular assembly-mode changing motions for 3-RPR parallel manipulators [J]. Mechanism and Machine Theory, 2008, 43(4) :480-490.
[2] BINAUD N, CARO S, WENGER P. Sensitivity comparison of planar parallel manipulators [J]. Mechanism and Machine Theory, 2010, 45:1477-1490.
[3] 韩霄,李虹,李瑞琴.基于BP法的3-RRP并联机构位置正解研究[J]. 组合机床与自动化加工技术, 2015(2): 94-97.
[4] 高晓雪,梅瑛,李瑞琴. 3-PPR平面并联机构的工作空间分析[J]. 机械传动, 2014, 38(2): 90-92.
[5] KALOORAZI M H F, MASOULEH M T, CARO S. Deter-mination of the maximal singularity-free workspace of 3-DOF parallel mechanisms with a constructive geometric approach[J]. Mechanism and Machine Theory, 2015, 43(4):25-36.
[6] 杜聿静, 王雷. 3-RRR并联机构灵巧度分析[J]. 机械工程与自动化, 2014,183(2):75-77.
[7] 史革盟,鲁开讲. 并联机构工作空间与奇异位形分析[J]. 机械传动, 2014(11): 54-59.
[8] HUSNG M Z, THEBERT J L. A study of workspace and singularity characteristics for design of 3-DOF planar parallel robot[J]. International Journal of Advanced Manufacturing Technology, 2010, 51(5): 789-797.
[9] 吴孟丽,张大卫,赵兴玉. 一种新型非对称并联机构的运动学分析[J]. 中国机械工程,2008(12):1423-1428.
[10] 贾晓辉,刘今越. 3-PRR柔性并联机构的优化设计[J]. 机械设计,2014(1):26-29.
Workspace and Dexterity Analysis of 3-RRP Planar Parallel Mechanism
LIUXiao-juan,LIHong,LIRui-qin,HAOLiang-liang,WANGHui
(School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, China )
The positive and inverse solution equations of the 3-RRP planar parallel mechanism are established, and the 3-RRP planar parallel mechanism and its structure block diagram are established by using the SimMechanics function module in Matlab/Simulink. The 3-RRP planar parallel mechanism workspace range is obtained by the sliding rod travel constraint programming.The dexterity of the contour line of the 3-RRP parallel mechanism is obtained by the condition number into the countdown to the dexterity analysis, the distribution of the whole workspace is uniform, and the kinematic of the mechanism is isotropic, and a variety of performance are also good. The results of the study for 3-RRP planar parallel mechanism takes as the theoretical basis for optimization design and dynamics research.
Matlab;parallel mechanism;workspaces;dexterity
1671-0444 (2016)04-0523-04
2015-12-02
国家自然科学基金资助项目(51275486)
刘小娟(1989—),女,山西忻州人,硕士研究生,研究方向为机构动态设计与优化. E-mail:994512601@qq.com 李 虹(联系人),女,副教授,E-mail:349824199@qq.com.
TH 124
A

