一种描述主体信息变化的交流图及其逻辑初探*

郭佳宏 张朝霞

一种描述主体信息变化的交流图及其逻辑初探*

郭佳宏 张朝霞

近年来，关于主体间通过交流而改变他们的知识和信念状态的形式化研究受到哲学等领域学者的广泛关注。交流图及其逻辑是其中的一项典型代表。我们考察研究帕奎特和派瑞克关于交流图逻辑的主要思想和技术，涉及拓扑逻辑和基于历史的模型等内容；采用其中的部分结果尝试解释若干有重大历史影响的问题，比如奥巴马如何获取本·拉登下落信息、“水门丑闻”背后的“深喉事件”等。最后还指出了交流图逻辑的几个可能的进一步应用。

信息流动 拓扑逻辑 交流图 基于历史的模型

本文旨在考察展示一种刻画主体的信息状态如何改变的表示方式，即聚焦于对主体间信息交流后的动态变化的描述。这种关于知识和信念的形式化模型中的动态转变的研究近来备受学者关注。相关工作以帕奎特（Eric Pacuit）和派瑞克（Rohit Parikh）的研究为典型，他们在文章《交流图的逻辑》中研究了一种包含交流算子的多主体认知逻辑，其中主要观点是：主体在一开始时拥有各自的私有信息，他们会通过与其他主体的交流获取一些信息后，对自己的原始信息进行提炼加工。根据这样的思路，不妨假设多个主体被一个交流图连接起来，在交流图中，从主体i到j的一个边（edge）的含义是：i能直接从j处获取信息。i通过获取j拥有的信息（可能还包括j从其他主体k处获取的信息）后，会对其原始信息进行提炼、更新。为了深入理解交流图的逻辑及其应用，首先有必要关注交流图的核心内容及其发展背景。

一、从拓扑逻辑到交流图

在文章《拓扑逻辑推理和关于知识的逻辑》（Topological Reasoning and the Logic of Knowledge）[1]中，摩斯（Moss）和派瑞克（Parikh）介绍了一种关于知识和努力的双模态逻辑—拓扑逻辑（Topologic），这种被称作拓扑逻辑的新逻辑也可以被看做包含努力算子的认知逻辑，它可以使关于状态和集合的推理形式化。认知算子和努力算子分别用符号K和◇表示，K的含义是：知道命题；◇的含义是：经过一些努力后为真。例如，公式→◇K就表示：如果是真的，那么经过一些努力，K是真的。换言之，如果是真的，那么经过一些努力主体就能知道。这里所谓“努力”的具体含义要视情况而定，它可以被解释为进行测量、运用计算等等，交流图中则把“努力”视作对其他主体的资料库中信息的咨询、获取等行为的综合。

某些数学结构，例如子空间、拓扑等都可运用语义框架对知识的获取进行详明解释。给出一个集合W，一个子空间是一个二元组〈W，〉，是W的子集作为元素组成的集合。一个状态x∈W是世界的一个完整描述，里面成立的原子信息用来表述基础事实（ground facts），而一个集U∈称作一个观察。二元组（x，U）称为相邻情境（neighborhood situation），可看做是一个真实情境加上基于该情境的观察。拓扑逻辑的公式就是在相邻情境中得到解释的。认知算子K表示在当前观察中的进展，努力算子◇表示对当前观察的提炼。子空间的通俗含义可概述为：W是世界中所有基础事实的集合，即它构成一个完整的可能世界集，其中的元素x是每个基础事实，其中每个子集U是一个观察，即某人某时刻所掌握的事实集。

文章《拓扑逻辑推理和关于知识的逻辑》中，展示了多主体拓扑逻辑，其中，努力算子◇被解释为主体间的交流。要使交流发生，我们必须保证参与主体能理解某种共同语言，因此，假设这个能被所有主体都理解的原子命题集为At，但只有特定主体在一开始时知道At中某部分元素的真值，这里用p，q…表示At中的元素。不过，每个主体在初始时都拥有一些私有信息，这些信息可以通过交流和其他参与主体分享，也可以通过从其他主体处获取一些信息对其原始信息进行提炼。因此，如果限制了主体与其他交流主体的联系，该主体能从其他主体处获取的知识也将被限制。

不妨考虑一个简例：美国总统奥巴马（Barack Obama）和美国中央情报局原局长帕内塔（Leon Panetta）曾经所处的某种情境。如果奥巴马想知道特工鲍勃（Bob）掌握的某个情报信息，他需要通过帕内塔来获取该信息。假设公式表示本·拉登（Osama bin Laden）的下落，鲍勃掌握了该信息（KBob），而那时奥巴马并不知道本·拉登的真实下落（￢KObama），但是他可以通过帕内塔得知本·拉登的下落（◇KObama），而普通人员e和r由于没有安全许可就不可能知道本·拉登的下落（￢◇Ke∧￢◇Kr）。显然，如果奥巴马获取了该信息，帕内塔必然也已经知道。我们可以用下面这个公式来表示两人的当时情境：￢KObama∧□（KObama→KPanetta），其中□是◇的对偶。这是因为奥巴马和鲍勃之间没有直接链接边，除非通过帕内塔来建立一个链接边。

上述例子都假定了主体i能获取j的所有信息，这是一个重要的理想化预设。要使这一理想化情境成为现实至少需要满足以下两个必要条件：首先，所有主体使用某个共同语言；其次，主体拥有的信息都是可用的，并且所有信息都是由主体使用的共同语言可表达的。

二、交流图的逻辑

（一）语言

模态公式Ki解释为“基于主体i的当前信息状态，他知道”或者直接为“主体i知道”；◇解释为“经过主体间的一些交流后为真”。于是，拓扑逻辑中公式→◇K解释为“如果是真的，那么经过一些交流努力后主体能知道”。基于多主体的上述公式交流图版本Kj→◇Ki就可理解为“如果主体j知道，那么经过一些交流后主体i知道”。

令At为命题变元符号组成的有穷集，p∈At是原子命题符号。则交流图的逻辑的语言按照BNF方式表述如下：

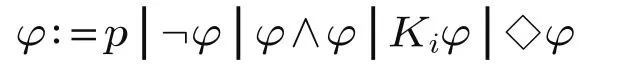
（二）语义

交流图逻辑的语义结合了前面提到的拓扑逻辑涉及的拓扑子模型和基于历史模型的语义。直观的意思是，给定一个交流图情况下，每个主体初始时都被给予一些信息，而后他们会依据交流图进行交流。这里介绍相关形式语义的意义就在于可以把主体初始知道的信息和交流后知道的信息清晰化表述。

主体i在初始时拥有部分命题变元集的真值情况，这部分命题集记作Ati。该知识是公共知识，即所有其他参与主体都知道主体i知道Ati的真值情况，但这些除i之外的主体初始时并不知道Ati的真值。如果Ati和Atj存在交叉部分，就表示主体i和j在初始时共享某部分信息。令V是At上的布尔赋值集，V中的元素υ可以理解成一个状态，用0和1分别表示值的假和真。初始时，每个主体i都被给予一个布尔赋值υi：Ati→｛0, 1｝，这种主体间信息的初始分布可用一个向量=（υ1, …, υn）来表示。这种初始的布尔赋值是可以相容的，比如在主体i和j的共享信息中，二者的布尔赋值可以是相同的，换言之，在Ati∩Atj的部分υi和υj保持一致。如果对每个∈dom(υi)∩dom(υj)，存在υi()= υj()，则称这部分布尔赋值的向量=（υ1, …, υn）是一致的（其中i， j在1，…，n中变化）。我们只把这些一致的向量作为主体的初始信息，所有这些初始信息都是公共知识，但它的真值情况υi是私有的（具有主体i独有的内容）。

根据上述定义，我们还需要考虑两个问题。第一个问题是并非所有的历史都是合法的。如果在一个历史序列中事件（i，j，）跟在历史H后边，则需要满足“H发生后，j知道”。显然i不可能从j处获取j不知道的信息。一个历史是否公正，不仅取决于其初始赋值，还取决于每个交流事件发生前的交流集。第二个问题在于：主体通过公式获取的信息可能比本身的真值内容更多。例如，i从j处得知而主体j和知道的真值的主体之间并没有链接边；在这种情境中，i不仅获取了的真值，也获取了的真值，因为j能得知的真值的唯一前提在于j知道是真的。以下关于语义的综述中将尝试处理上述两个问题。

对于交流图模拟的实际环境，每个主体可能面临的不确定性有两种：首先是主体对世界真实状态的不确定，其次是主体对哪个交流事件会发生的不确定。

假设主体i与j有直接链接边，j与k和m有直接链接边，k和m都与r有直接链接边，并且r知道是真的。则m通过r的网站获知的真值，j通过m获知是真的同时也获知了是稳定公式。尽管i知道是真的，但是他并不知道，因为仅从j的网站上，i并不能排除j是通过k来获知的可能性。这个例子或许可以用来解释“水门丑闻”背后的“深喉事件”：深喉（Deep Throat），是指在水门事件中为记者提供重要资料的人。1972年，美国《华盛顿邮报》记者鲍勃·伍德沃德（Bob Woodward）和卡尔·伯恩斯坦（Carl Bernstein）依据线人“深喉”的消息，捅开“水门事件”的内幕，导致当时的美国总统尼克松辞职下台。上述事件显然至少涉及两位记者和线人的信息交流以及美国民众从记者那里获取信息（通过《华盛顿邮报》）这样的认知活动。在此后长达30多年的时间里，伍德沃德和伯恩斯坦一直保守秘密，拒绝向外界透露“深喉”的身份，直到2005年马克·费尔特（Mark Felt）承认自己就是当年“水门事件”中的神秘线人。我们提这一交流事件的要点在于当年关心政治的美国民众知道两位记者明白“深喉”是谁，但他们并不知道伍德沃德和伯恩斯坦是如何得知的。“水门事件”背后的秘密究竟还有多少？也许人们永远无法知道。

为处理合法或公正历史的概念，帕奎特等引入命题符号L，用来表示它只有在合法历史(, H)下才是可满足的。他们也用L (, H)来表示(, H)的合法性。由于L仅能由知识获得定义，而知识的定义基于量化的合法历史，因此，对L和(, H)的合法性应给予互推定义。由此，他们给出交流图及其对应的模型和有序对(, H), 定义(, H)的合法性和公式在模型上的可满足情况如下：

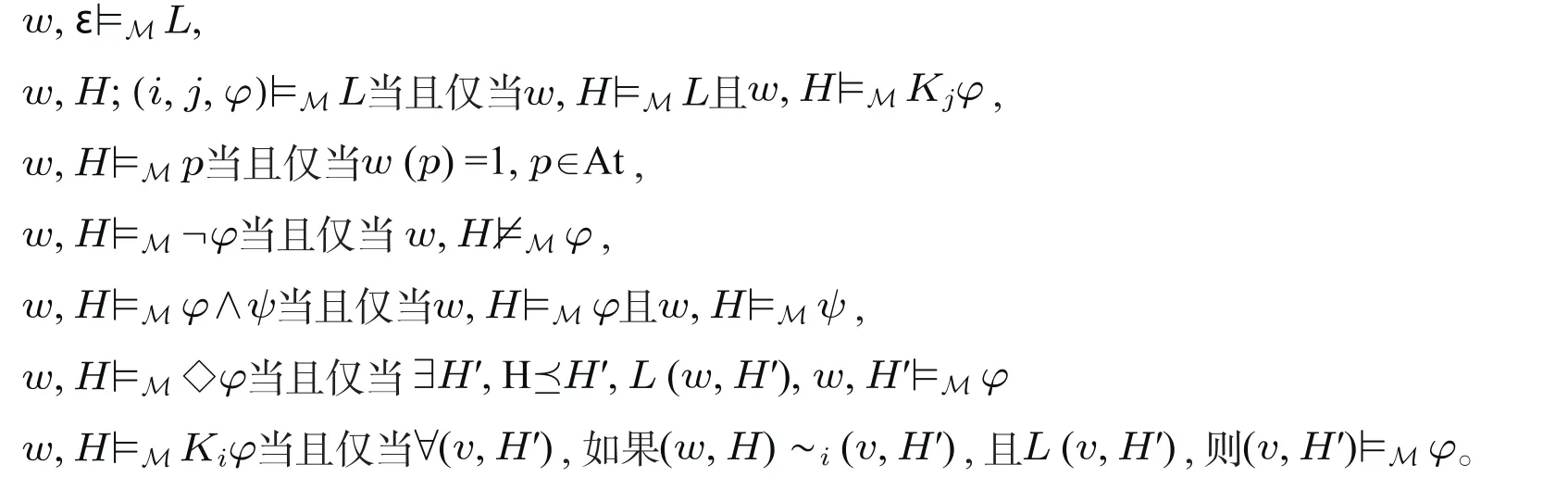
（三）逻辑

以下公理和规则构造而成的逻辑系统，相对于所有的子空间集是可靠和完全的。它们是任意拓扑逻辑的核心公理和规则集。[7][8]1. 所有命题重言式

三、总结与进一步研究

我们研究了帕奎特等学者关于知识和交流的逻辑系统，主体之间的交流受当下情境下所对应的交流图的限制，主体可以在其他主体未察觉的情况下获取他人的知识。一个交流图的性质是由基于该交流图模型所有有效的公式定义的，这样构建的交流图逻辑是可判定的。

在交流过程中有关信息更新和知识获取的逻辑是最近学术研究的热点。现在可以比较一下相关方法的同异。一种有影响的方案是以阿姆斯特丹学派为代表的动态认知逻辑，这些逻辑运用PDL（命题动态逻辑）算子来表达信息更新。[10][11]例如，如果!的含义是“公开宣告”，则的含义是“公开宣告后，主体i知道”。从这个观点看，交流算子◇可被理解为个人认知更新序列的存在量化。这里的语义与动态认知逻辑的语义有一些不同。首先，这里交流受到交流图的限制；其次，他们没有考虑一些文献中对一般的认知更新的研究，而是研究了一种特殊的认知更新及其与交流图的联系。最重要的是，交流的历史在知识的定义中起着关键作用。动态认知语义的一般做法是：通过定义更新算子把一个关系结构映射到另一个关系结构上，以表达第一个关系结构上认知更新的效果。例如，的一个公开宣告所在的关系子模型中，在每个状态都为真。认知更新后知识的定义是常规定义，即在认知更新关系结构中，如果在所有对i而言与可达的状态中都为真，则称i在状态上知道。

用交流图刻画社会软件的工作[12]在未来有很大的延伸空间。例如，找寻一个漂亮的完全性公理、找寻可表达其他不同类型的更新或修正的语言，如谎言、意识到的更新（主体j意识到他的“网站”被其他主体进入）等等、找寻能表达主体在进入其他主体网站时存在偏好的情境语言。这些研究工作目前都有学者在做，并且部分取得了重要的阶段性结果。[13][14]

最后，需要指出的是，交流图的逻辑框架还可被作为加密协议的示范。不过，在研究时需要注意两个重要问题。第一个问题是，主体可能只想让他的“网站”中的一部分知识被其他主体获取，这可通过在框架中把主体j的知识限定成想让其他主体获取的公式而得，通过限制后，如果主体i和j有直接链接边，i也只能通过那部分可获取的信息进行认知更新；第二个问题是，交流图中的主体可能并不知道交流图的真实结构。例如，如果A能通过B的网站获取一些信息，A不知道的是，C能窃听到这些，即交流图中就存在C和B间的链接边，而A和B并不知道这个边的存在。显然，A从B处获取的信息也会被C获取。为避免这一问题，研究加密协议时需要确保交流图中不存在主体不想要的链接边。这也是交流图未来研究的方向之一。

[1][8] L. Moss and R. Parikh，“Topological Reasoning and the Logic of Knowledge”，Y. Moses (Ed.), TARK IV, Morgan Kaufmann, 1992.

[2][3][6][7][9] E. Pacuit and R. Parikh，“The Logic of Communication Graphs”，Proceedings of DALT 2004 (2005), J. Leita, A. Omicini, P. Torroni and P. Yolum (Eds.), no. 3476 in Lecture Notes in AI, Springer, pp. 256 - 269.

[4] E. Pacuit and R. Parikh，“Reasoning About Communication Graphs”，J. van Benthem, D. Gabbay and B. Loewe (eds), Interactive Logic - Proceedings of the 7th Augustus de Morgan Workshop, Texts in Logic and Games, Amsterdam, 2007, pp.135 -157.

[5] P. Blackburn, M. de Rijke and Y. Venema，Modal Logic，Cambridge: Cambridge University Press, 2001.

[10] J. van Benthem, H. van Ditmarsch, J. van Eijck and J. Jaspars，Logic in Action，Open Course Project, http://www. logicinaction.org/（2015/6/4），New Edition February 7, 2014.

[11] H. van Ditmarsch, W. van der Hoek and B. Kooi，Dynamic Epistemic Logic，Springer, 2007.

[12] 郭佳宏、张朝霞：《社会软件及其认知逻辑分析》，《自然辩证法研究》2013年第9期。

[13] 刘奋荣：《动态偏好逻辑》，北京：科学出版社，2010年。

[14] H. van Ditmarsch，“The Ditmarsch Tale of Wonders”，Lecture Notes in Computer Science，vol.8736, 2014.

责任编辑：罗 苹

B815.3

A

1000-7326（2016）12-0030-06

*本文系中央高校基本科研业务费专项资金资助项目、教育部留学回国人员科研启动基金项目“程序性知识的逻辑研究”、国家社科基金重大项目“应用逻辑与逻辑应用研究”（14ZDB014）的阶段性成果。

郭佳宏，北京师范大学哲学学院价值与文化研究所副教授（北京，100875）；张朝霞，郑州市交通运输委员会（河南 郑州，450006）。