基于灰色关联度的PPP项目私营部门的选择模型
任志涛,胡 欣,王滢菡,武继科
(天津城建大学 经济与管理学院,天津 300384)
经济与管理
基于灰色关联度的PPP项目私营部门的选择模型
任志涛,胡 欣,王滢菡,武继科
(天津城建大学 经济与管理学院,天津 300384)
公私合作(PPP)项目中,公共部门选择合适的私营部门“联姻”是项目成功的关键因素之一.运用文献频数分析法甄选出评价私营部门的有效指标,并从财务能力、技术能力、管理能力、过往经验以及声誉水平五方面建立相应的指标体系;运用熵值法来确定各项指标的权重.以灰色加权关联度高低为遴选评价方案的依据,基于灰色关联理论构建PPP项目公共部门选择私营部门的决策模型,并通过实例论证该模型的实用性及有效性,为PPP项目私营部门选择提供一种路径.
公私合作;灰色关联度;私营部门;选择模型
公私合作(public private partnership,简称PPP)是公共部门和私营部门建立在责任与风险共担、资源和利益共享基础上,提供公共服务的一种长期合作伙伴关系.其中私营部门的参与带来丰富的社会资本和先进技术及管理经验,缓解政府财政压力,提高公共服务的供给效率,在项目建设运营中起着至关重要的作用.公共部门作为PPP项目的主导者,对私营部门科学合理地选择是项目成功的关键要素之一.实践中,公共部门对私营部门的选择存在指标粗略、选择方法单一的问题,故公共部门如何甄选评价私营部门指标,合理选择私营部门,是重要的研究课题.
目前,国外学者在选择私营部门的评价方法上对模糊综合打分法、模糊层次分析法、DEA(数据包络法)等做出尝试[1-6];国内学者的研究则大多着力于私营部门评价标准及指标权重的确定[7-9],对私营部门的选择方法,仅陈通等[10]在构建基于技术能力、可持续发展能力和关系型合约管理能力的指标体系基础上,通过建立基于AHP(层次分析法)的多目标决策模型进行研究;此外,运用灰色关联思想构建选择模型的研究也较广泛,如刘琦等[11]利用灰色关联度构建知识伙伴联盟选择模型,王军武等[12]将其应用于建筑供应商的选择研究.但总体来看,已有研究对私营部门指标选取的精细度与PPP项目的匹配度有待深入,私营部门选择方法研究也需从科学实用的角度来丰富,同时目前将灰色关联思想应用于PPP项目私营部门选择的研究文献也很少.基于此,本文将通过文献频数分析的方法甄选评价私营部门的指标、构建系统的指标体系,运用灰色关联度分析的方法对PPP项目私营部门的选择进行研究,以期为PPP项目中公共部门对私营部门的科学合理选择提供借鉴.
1 PPP项目私营部门选择评价指标甄选原则与体系构建
1.1 PPP项目私营部门评价指标的甄选原则
PPP项目不同于普通的工程项目:一方面,其投资规模大、建设运营期长的特性要求私营部门具备雄厚的资金支持能力和先进的技术以及管理经验等刚性条件;另一方面,公私双方利益需求的差异性导致双方产生博弈,要求私营部门具备一定的社会责任感、商业信誉等柔性条件.故政府对私营部门评价指标的甄选应区别于普通工程项目业主对投标方评价指标的选取,需结合PPP项目的特殊性遵循一定的原则,借鉴已有学者的研究[12-13],认为私营部门评价指标甄选应遵循以下原则.
(1)契合私营部门选择的根本目标需求.公共部门对私营部门的选择以整合私营部门资源优势、弥补项目所必需而自身缺失的优势为目标,所以指标的选取应以该目标为导向有的放矢,选择可以衡量私营部门相应能力与优势的指标,从而提高评价私营部门能力的准确性.
(2)指标选择精炼,且具有代表性.评价指标应尽可能精炼,数量过多易造成指标内容间的重复,数量过少则无法描述私营部门的重要信息,这都会干扰评价结果的准确性;同时,选取的各个指标之间应当具有差异性,能代表私营部门在某一方面的特性,确保指标选取的有效性.
(3)具有实用性和可操作性.私营部门评价指标的选取在精炼和具有代表性的基础上,还要考虑其实用性和操作性,脱离实际和缺乏操作的指标对私营部门的选择并无实际意义.
1.2 PPP项目私营部门选择评价指标体系的构建
文献频度分析法是归纳分析现有研究成果中的指标体系,通过统计找出频数较高指标,并构建相应指标体系.依据PPP项目私营部门评价指标甄选的原则,通过文献频度统计分析方法,识别出其中出现频率较高的私营部门评价指标[1-4,7-10,13-19],从财务、技术、管理、过往PPP项目经验及社会声誉五方面出发,将以上指标进行分类整理,从而构建一个由5个二级指标及22个三级指标构成的PPP项目私营部门选择评价指标体系.该体系指标选取较精细,综合考虑了PPP项目中私营部门的各项必备能力、提高指标与PPP项目的匹配度,其具体结构如图1所示.
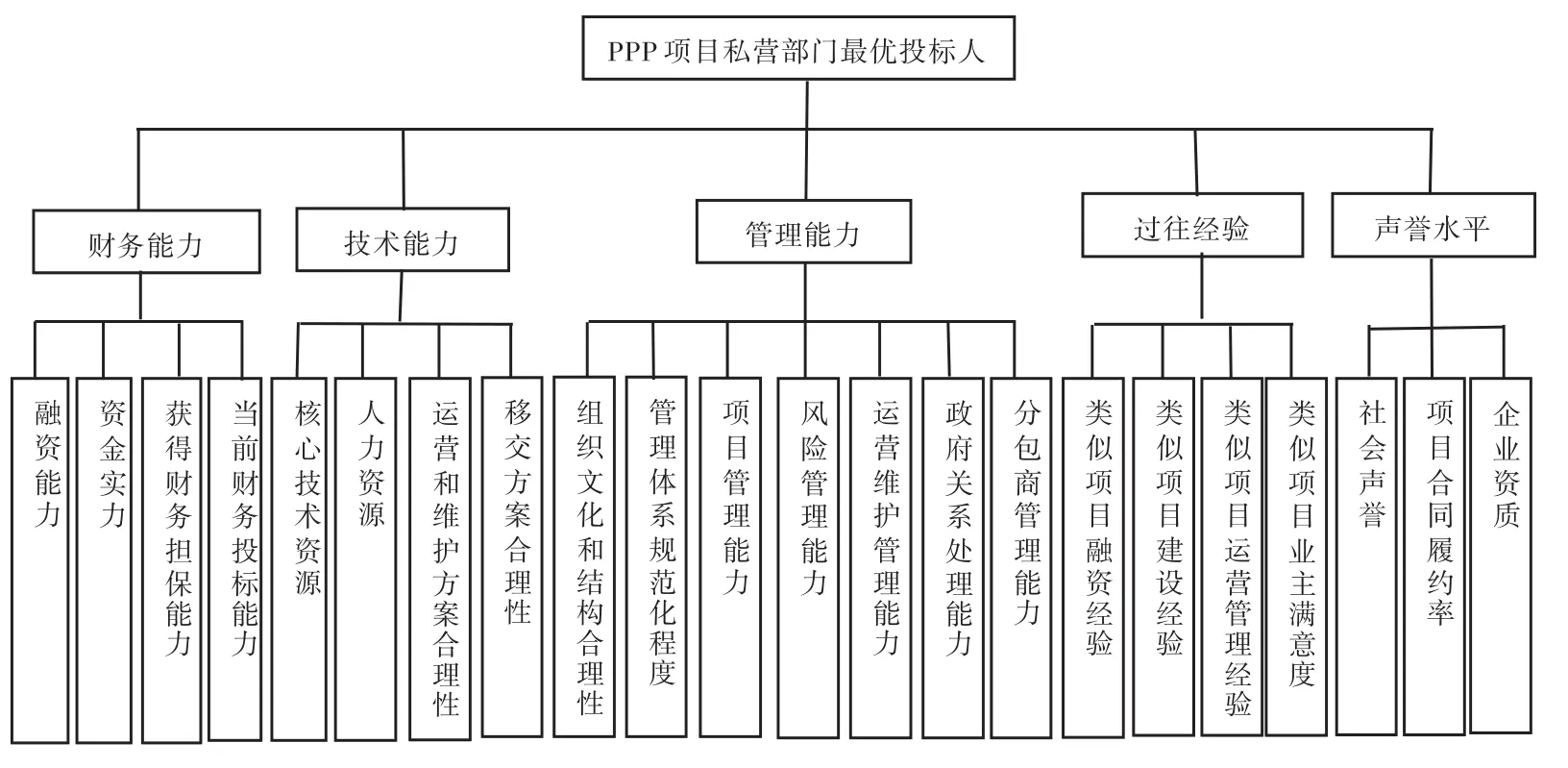
图1 PPP项目私营部门评价指标体系
2 基于灰色关联度的PPP项目私营部门选择评价模型的构建
灰色关联分析(grey relation analysis),其理论思想是根据因素序列曲线几何形状的相似度来判别联系的紧密程度,若序列曲线越接近,则关联程度越高,反之越低[20].故通过被评价方案与最优参考方案之间灰色关联度的高低,可排序参与评价的PPP项目各私营部门方案.相比传统评价方法,灰色关联分析对样本数量及分布规律并无太大要求,且计算工作量小,因此在数据资料较少的情况下更具实用性[21-22].该方法使PPP项目中公共部门评选私营部门的工作量减少,评选结果稳定,且具有科学性.
本文首先设定一个最优方案为参考序列,然后计算各备选方案与最优方案之间的关联程度,并进行排序选出最佳方案.
2.1 问题的条件及假定
假设参与竞争PPP项目的私营部门有n个,即最终待评选的方案有n个,记为X={x1,x2,…,xn};评价指标有m个,记为V={v1,v2,…,vm};方案xi关于第j个指标vj的指标值用xij(i=0,1,2,…,n; j=1,2,…,m)表示,则n个方案的mn个指标值构成矩阵Z=(xij)n×m,记作X={x1,x2,…,xn}对V={v1,v2,…,vm}的评价矩阵,提供公共部门对私营部门的分析评价信息.
通常指标包括效益型、成本型及适中型:效益型指标值大而优,成本型指标值小而优,适中型指标值居中而优.文中所建立的指标体系,22个三级指标均系效益型定性指标.为使评价更具可操作性和实用性,需要将其转化为定量指标,将定性指标的分值限定在固定区间[0,10],专家对私营部门某项评价指标的满意度越高,分值就越高,某一定性指标最后分值由不同专家评价分值的加权平均计算所得.
2.2 最优参考方案的确定
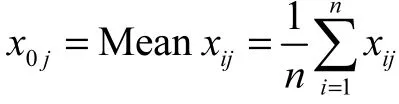
各指标之间量纲和数量级的差异会影响评价结果的科学准确性,故评价决策前须对各项指标进行无量纲处理.用数列x的初始值x(1)除以数列x中的每一个数,得到一个新的序列,可记为:x→x′.
初值化的序列没有量纲,且有公共交点xi(1)=1,公式为[23]:
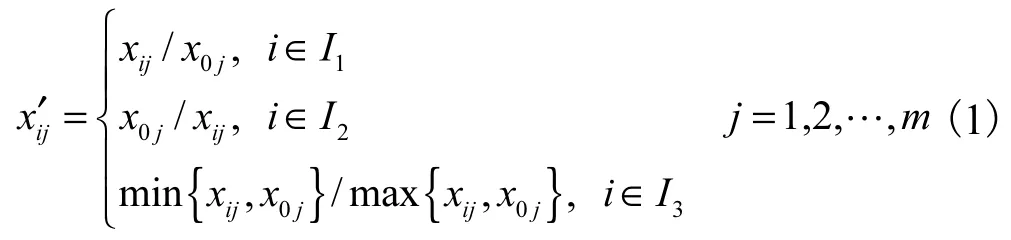
其中,I1、I2、I3分别代表效益型、成本型和适中型的下标集合,由此可得到新矩阵A′=(xi′j)(n+1)×m为A=(xij)(n+1)×m的初始化矩阵.显然,最优参考方案经过初值化后变为x0′j=1(j=1,2,…,m),x0′=(x0′1,x0′2,…,x0′m)=(1,1,…,1 ).
2.3 待评选方案的关联度计算
将最优参考方案x0用向量表示为x0′=(x0′1,x0′2,…,x0′m)=(1,1,…,1),并将其作为参考序列,即母序列,待评价方案xi用向量xi′=(xi′1,xi′2,…,xi′m)表示,其为子序列,x0′与xi′在第j点指标的数分别为x0′j与xi′j,将x0′与xi′在第j点指标的关联系数定义为rj(x′i,x0′),记作rij,计算公式为[24]:
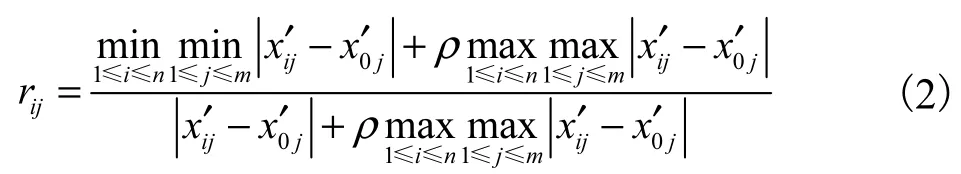
其中,ρ称为分辩率系数,ρ∈(0,1),通常取ρ=0.5.引入ρ来减弱最大绝对差数值过大而产生的失真现象,使关联系数间的差异显著程度得以提高.
定义n×m个灰色关联系数rij( i=1,2,…,n; j=1,2,…,m)构成的矩阵为灰色关联矩阵,记为
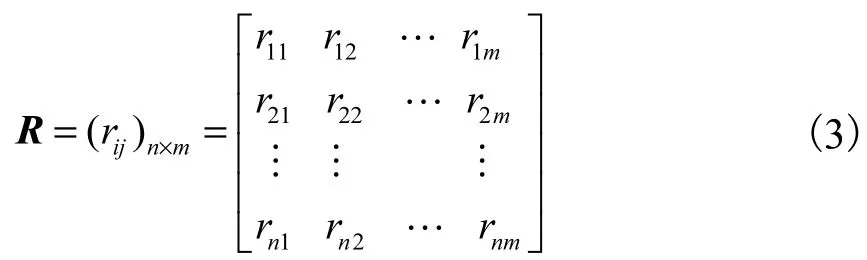
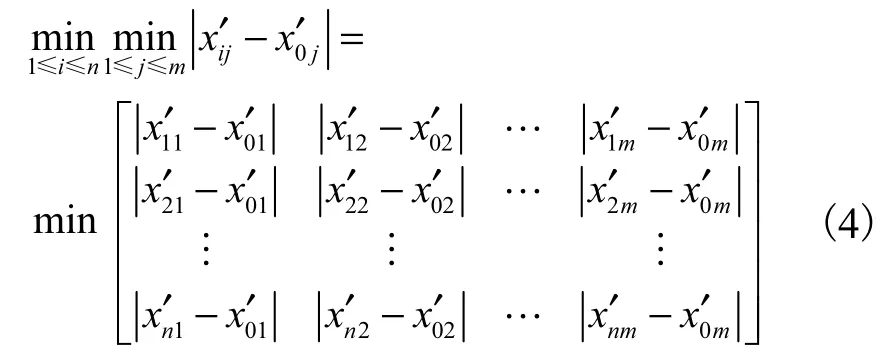
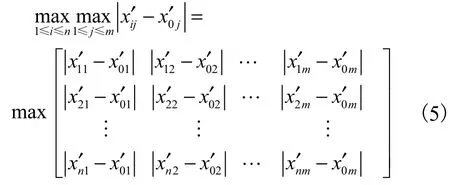
公式(2)计算的灰色关联系数rij只表示子序列中指标xi′j与母序列中对应指标x0′j的关联程度,要表示待评价方案xi与最优参考方案x0的关联程度,可采用加权关联指标ξi表示,其计算公式为

式中:ωj称作指标vj的权系数;ξi实际意义为子序列xi′与母序列x0′中全部指标关联系数rij加权后的平均值,假设方案x0与xi的关联度为ξi,x0与xj的关联度为ξj.当ξi>ξj时,则方案xi优于xj;当ξi=ξj时,则方案xi等价xj;当ξi<ξj时,则方案xi劣于xj.
2.4 利用熵值法确定评价指标权重[25]
指标权重的大小直接关系到最后公共部门对私营部门的选择结果,故科学地确定各指标权重是PPP项目中公共部门选择合适私营部门的关键之一.利用信息论中的熵技术来确定各指标的权重,将权重向量表示为
考虑n个方案、m个指标所构成的矩阵为

设第i个方案中的第j个指标的数据为xij( i=1,2,…,n ;j=1,2,…,m).对于给定的j,若相应xij的差异越大,表明该项指标对私营部门评价系统的比较作用相应越大,也即同一指标不同方案的值差异越大,证明该项指标所包含和传导的信息越多.熵就是用来度量这种信息量的大小,信息的增加意味着熵的减少.用熵值法确定指标权重的步骤如下:
(1)计算第i个方案在第j项指标下,指标值的特征比重Pij


(2)计算第j项指标的熵值,即

式中:k>0,ej>0,且k=1/ln n,当确定参与竞标的私营部门个数时,k将是一个确定的常数.
(3)计算第j项指标的差异性系数.对于给定的j,xij的差异性与ej成反向:xij的差异越小,则ej越大;若xij全部相等,此时ej=emax=1(k=1/lnn)对于系统间的比较,指标xj并无作用;若xij的差异越大,则ej越小,指标xj对私营部门评价系统的作用越大.故定义差异系数为:

其中jg越大,说明该指标越重要.
(4)确定权数jω

则jω就是用熵值法来表示的第j项指标的权重因子.
2.5 综合评价决策模型
通过以上的分析可得到待选方案的灰色关联矩阵为R=(rij)n×m(i=1,2,…,n;j=1,2,…,m),m个评价指标相对于总目标的权值向量为W=(ω1,ω2,…,ωm)T,则各待评价方案xi与最佳参考方案x0的加权灰色关联度组成的灰色关联向量为ξ=(ξ1,ξ2,…,ξn).
依据灰色关联决策相关理论,以被评价方案的加权灰色关联度高低评价PPP项目私营部门方案优劣.首先计算ξi,然后根据ξi的大小排出关联序高低:ξi越大,关联程度越高,表明第i个私营部门提供的方案xi越接近于最优参考方案x0.因此,政府应选择的私营部门为ξi值最大、关联序最高的那个,即ξi=max(ξ1,ξ2,…,ξn).
3 实例分析
3.1 项目概况
某收费高速公路项目采用PPP方式建设运营,其建设运营期为30年,投资总额为62.35亿元.公共部门利用公开招标的方式选取私营合作伙伴,经过前期的比较筛选,最终有A、B、C、D四家私营部门参与到最后的竞标阶段,公共部门组织富有PPP项目经验的相关专家学者进行评标.各专家根据不同私营部门的具体情况,对照事先拟定的评分标准逐项进行打分评标,最后对专家们的打分简单加权平均后,得到四家私营部门各项指标的评价值如表1所示.通过分析PPP项目私营部门各项指标与最优参考方案各指标关联程度的高低,找出最佳的私营部门合作伙伴.
3.2 模型应用
根据基于灰色关联思想构建的PPP项目公共部门决策模型,选择最佳私营部门.

表1 四家私营部门所供方案各指标评价值
根据表1,最优参考方案的因素指标为
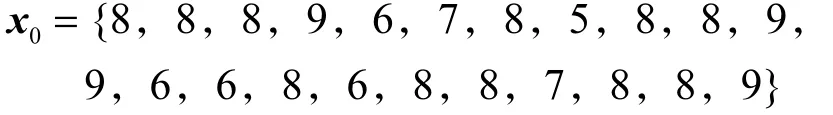
根据式(2)计算灰色关联系数rij,灰色关联矩阵R=(rij)n×m为

根据熵值法计算各指标权重,由式(10)确定各指标权数ωj

最后,将式(3)和式(10)代入式(6),求出各方案与最优参考方案的加权灰色关联度ξi,其构成的向量记为ξ
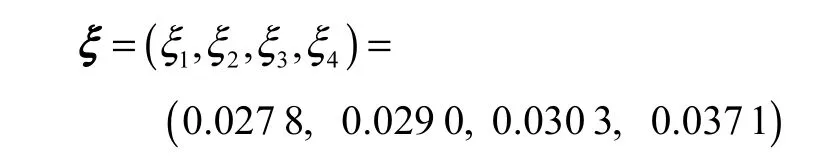
由ξ4>ξ3>ξ2>ξ1,可知4个待评价的私营部门方案由高到低依次为:方案4,方案3,方案2,方案1.根据灰色关联评价的核心思想,显然方案4最优.该结果吻合于表1中数据的实际意义,可以看出本文所提出的PPP项目政府对私营部门的选择决策方法是有效的.
4 结 论
(1)PPP项目私营部门选择决策系统属于灰色系统,运用灰色关联思想解决私营部门选择问题,使得PPP项目私营部门选择更具科学性.
(2)对PPP项目私营部门选择决策模型的构建有规范的步骤:首先确定决策矩阵,并对其初始化;其次计算灰色关联矩阵及指标权重;最后确定各方案与最优参考方案的加权灰色关联度向量.
(3)针对私营部门选择的多目标性,构建基于灰色关联度分析的公共部门决策模型,该模型的有效性及实用性通过实例得到验证.
本文采用文献频度分析法构建指标体系,由于文献搜集可能存在的不完全性等,导致该指标体系具有一定的主观性,更为科学的指标体系的构建还需深入研究.希望通过本文研究,为PPP项目私营部门选择提供一种可行路径.
[1] ZHANG Xueqing. Concessionaire selection:methods and criteria[J]. Journal of Construction Engineering and Management,2004,130(2):235-244.
[2] ZHANG Xueqing,Criteria for selecting the privatesector partner in public private partnerships[J]. Journal of Construction Engineering and Management,2005,131(6):631-644.
[3] ZHANG Xueqing. Best value concessionaire selection through a fuzzy logic system[J]. Expert Systems with Applications,2009,36(4):227-254.
[4] KUMARASWAMY M M,ANVUUR A M. Selecting sustainable teams for PPP projects[J]. Building and Environment,2008,17(43):99-109.
[5] WU Qian,GAO Yanan. Selection model of concessionaire in PPP projects[J]. Applied Mechanics and Materials,2012,180(174):108-130.
[6] El-MASHALEH M S,EDWARD R M. Concessionaire selection model based on data envelopment analysis[J]. Journal of Management in Engineering,2013,131 (5):484-494.
[7] 张 轶. 风险分析下的PPP模式私营合作者选择方式研究[J]. 现代商业,2010,10(17):173-174.
[8] 国翔宇. BOT项目特许经营者选择标准研究[D]. 大连:大连理工大学,2011:8-51.
[9] 黄亚江,张水波. 基于ANP理论的PPP项目私营部门选择研究[J]. 项目管理技术,2012,10(6):46-51.
[10] 陈 通,杜泽超,姚德利. 基于AHP的PPP项目中私人投资部门的选择模型研究[J]. 曲阜师范大学学报(自然科学版),2011,37(3):6-10.
[11] 刘 琦,陈 琼,韦司滢. 基于多层灰色关联度的知识联盟伙伴选择模型[J]. 华中科技大学学报(自然科学版),2004,32(7):54-56.
[12] 王军武,呙淑文. 基于灰色关联度的建筑供应商选择方法研究[J]. 武汉理工大学学报,2007,29(3):153-156.
[13] 赵 阳. BOT项目特许经营者选择研究[D]. 大连:东北财经大学,2013:9-55.
[14] 王 薇,戴大双,王东波. 广西来宾B电厂BOT项目特许经营者选择研究[J]. 科技与管理,2011,13(2):96-99.
[15] 程言家. 基础设施PPP模式中特许权获得者的选择研究[D]. 南京:南京航空航天大学,2008:8-66.
[16] 关 夏. 工程总承包项目招标资格预审研究[D]. 北京:北方工业大学,2010:12-63.
[17] HATUSH Z,SKIMORE M. Criteria for contractor selection[J]. Construction Management and Economics,1997,15(1):19-38.
[18] 徐东明. 基于绩效预测的工程项目施工承包商选择模型[D]. 西安:西安建筑科技大学,2006:12-57.
[19] 杨晓辉. 绿色理念下EPC项目总承包商选择研究[D].哈尔滨:哈尔滨工业大学,2011:15-65.
[20] 刘思峰,党耀国,方志耕,等. 灰色系统理论及其应用[M]. 北京:科学出版社,2010:13-15.
[21] SHEN L Y,TAM W Y V,CHAN C W S,et al. An examination on the waste management practice in the local construction site[J]. Hong Kong Surveyor,2002, 13(1):39-48.
[22] 王家远,袁红平. 基于系统动力学的建筑废料分类分拣管理模型[J]. 科技进步与对策,2008,25(10):74-78.
[23] 罗 党,王洁方. 灰色决策理论与方法[M]. 北京:科学出版社,2012:41-65.
[24] 邓聚龙. 灰理论基础[M]. 武汉:华中科技大学出版社,2003:87-437.
[25] 郭亚军. 综合评价理论、方法及拓展[M]. 北京:科学出版社,2012:31-148.
Study on the Selection Model of Private-sector in PPP Project Based on Gray Relevancy
REN Zhitao,HU Xin,WANG Yinghan,WU Jike
(School of Economics and Management,TCU,Tianjin 300384,China)
In the PPP project,the public-sector choosing an appropriate private-sector establishing “Marriage’’ relationship is one of the key factors for success. First,constructing the index system of private-sector based on the document frequency method,which considered financial ability,technical skills,management ability,past experience and reputation level. The entropy value method is used to determine the weight of indexes,and the grey relation theory is used to measure grey correlation degree of evaluation schemes so as to construct government decision-making model of the selection of private-sector in PPP project. Finally,a case is given to prove that the model is practical and effective,which provides a path for private-sector choosing of PPP project.
PPP;the grey correlation degree;private-sector;selection model
C931.2
A
2095-719X(2016)06-0444-06
2015-11-08;
2016-03-04
教育部人文社会规划基金项目(11YJA630090);天津市教育科学规划“十二五”重点课题(HE2008)
任志涛(1968—),女,河北邯郸人,天津城建大学教授,博士.

