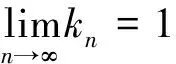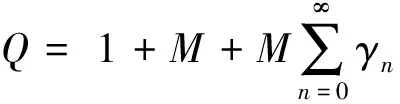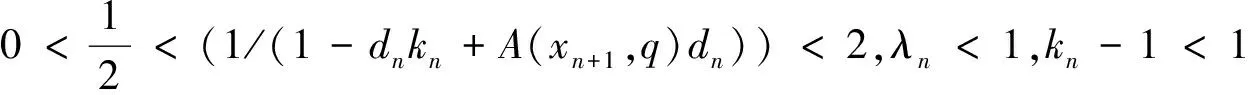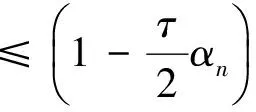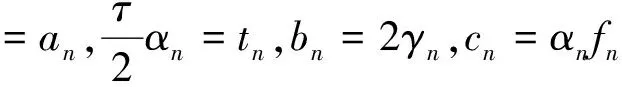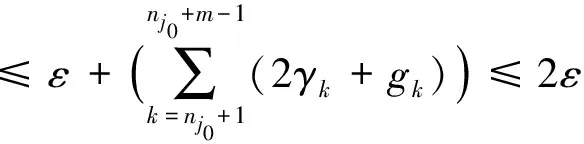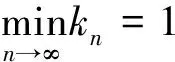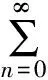渐近伪压缩型映象Noor三步迭代序列的收敛性
张树义,刘冬红,丛培根
(渤海大学 数理学院, 辽宁 锦州 121013)
渐近伪压缩型映象Noor三步迭代序列的收敛性
张树义*,刘冬红,丛培根
(渤海大学 数理学院, 辽宁 锦州 121013)
渐近伪压缩型映象; 渐近非扩张映象; 混合型误差; Noor三步迭代序列
0 引言与预备知识
全文设E是实Banach空间,E*是E的对偶空间.对偶映象Jp:E→2E*(1 T称为一致Lipschitz的,若存在L≥1,使∀x,y∈D(T),∀n≥1,有‖Tnx-Tny‖≤L‖x-y‖. 定义2 设D是E的非空凸子集,T:D→D是一个映象,∀x0∈D,由下式定义的序列,{xn}n≥0⊂D,{yn}n≥0⊂D (1) 其中{αn}n≥0,{βn}n≥0,{γn}n≥0,{μn}n≥0,{δn}n≥0和{ζn}n≥0为[0,1]中六个满足某些条件的实数列,{un}n≥0,{vn}n≥0和{wn}n≥0为D中的有界序列,则称{xn}n≥0为T的带混合型误差的修改的Noor三步迭代序列.特别地,当μn=0,∀n≥0,时,称由(1)所定义的序列{xn}n≥0为带误差的修改的Noor三步迭代序列.当γn=μn=δn=0,∀n≥0,时,称由(1)所定义的序列{xn}n≥0为带误差的修改的Ishikawa迭代序列. 引理1〔1〕设∀x,y∈E,则∀α>0,‖x‖≤‖x+αy‖成立⟺∃f∈Jx, 使〈y,f〉≥0. 由引理1容易推出下面引理2成立. (2) ‖xn+1-q‖≤‖xn+1-q+α[kn(xn+1-q)+A(xn+1,q)q-(Tnxn+1-q+A(xn+1,q)xn+1)]‖, 其中 关于渐近伪压缩映象和渐近非扩张映象不动点的迭代逼近问题的研究,文〔3〕得到了如下结果: (i)αn+γn≤1,δn+βn≤1; 近些年来, 文〔4-23〕研究了一些非线性映象不动点的存在性与迭代逼近. 受上述工作启发, 本文的目的是进一步研究渐近伪压缩映象和渐近非扩张映象不动点的迭代逼近问题, 从以下几方面对定理1进行推广和改进: (ii) 用{Tnyn}n≥0有界取代T的值域T(D)有界. (v) 将带误差修改的Ishikawa迭代序列推广到更一般的具混合误差的修改的Noor三步迭代序列. 需要指出的是在我们去掉定理1的条件时,并没有增加其它条件,因此本文改进和推广了文〔3〕中的主要结果,同时,本文结果也推广和改进了其他人的相关结果. (i)αn+γn+μn≤1,δn+βn≤1; ‖zn-q‖=‖(1-ζn)(xn-q)+ζn(Tnxn-q)‖≤Q(L+1), ‖yn-q‖=‖(1-βn-δn)(xn-q)+βn(Tnzn-q)+δn(vn-q)‖≤Q(1+L(L+1))+M:=B, ‖xn+1-yn‖≤βn(‖xn-q‖+L‖xn-q‖)+δn(‖xn-q‖+‖vn-q‖)+αn(L+1)‖yn-q‖ +γn(‖yn-q‖+‖un-q‖)+μn(‖yn-q‖+‖wn-q‖) ≤(βn+δn)(L+1)Q+αn(1+L)B+(γn+μn)(B+M), 从而‖Tnxn+1-Tnyn‖≤[(δn+βn)+αn+(γn+μn)]R,其中R=max{L(L+1)Q,L(1+L)B,L(B+M)}. 令dn=αn+γn+μn, 由(1)式有下列等式成立 (1-dn)xn=(1-dnkn)xn+1+dn(knxn+1-A(xn+1,q)xn+1)-dnTnxn+1+dnA(xn+1,q)xn+1 +dn(Tnxn+1-Tnyn)+γn(Tnyn-un)+μn(Tnyn-wn), (1-dn)q=(1-dnkn)q+dn(knq-A(xn+1,q)q)+dnA(xn+1,q)q-dnq. 据此可得 (1-dn)(xn-q)=(1-dnkn+A(xn+1,q),dn). +dn(Tnxn+1-Tnyn)+γn(Tnyn-un)+μn(Tnyn-wn). ‖xn+1-q‖≤(1-A(xn+1,q)αn)‖xn-q‖+2γn‖xn-q‖+4αn(kn-1)‖xn-q‖+αnfn+gn. (3) 其中fn=2λn(Rdn+M)+2Rdn,gn=2Rdn(δn+βn)+2γnM+2dnγnR. (4) 1+‖xnj+1-q‖p+Ψ(‖xnj+1-q‖)-Hnj≤1+Qp+Ψ(Q),所以 下面证明m≥1,有‖xnj0+m-q‖<2ε.当m=1时, 显然成立;当m=2时, 若 ‖xnj0+1-q‖<ε,则‖xnj0+2-q‖<ε+gnj0+1+2γnj0+1;若‖xnj0+2-q‖≥ε由Ψ的严格增加性有 由(3)式有 ‖xnj0+2-q‖≤(1-A(xnj0+2,q)αnj0+1+4αnj0+1(knj0+1-1))‖xnj0+1-q‖+2γnj0+1‖xnj0+1-q‖ +αnj0+1fnj0+1+gnj0+1 注1 条件D+D⊂D只用于保证迭代序列{xn}n≥0是有意义的,当ζn=μn≡0时,迭代序列即为文〔1〕中的迭代序列{xn}n≥0,此时当ζn=μn≡0时,条件D+D⊂D可以去掉. 由定理2可得定理3. 注2 在本文定理2的证明中{Tnyn}有界条件起了重要作用,那么按本文证法{Tnyn}有界条件是否可以去掉呢? 这值得我们做进一步研究. 〔1〕KATO.T. Nonlinear semigroups and evolution equation〔J〕. J. Math. Soc. Japan, 1967, 19(4): 501-519. 〔2〕倪仁兴. 一类广义Lipschitz非线性算子的带误差的Ishikawa迭代程序〔J〕. 数学学报,2001,44 (4): 701-712. 〔3〕曾六川. Banach空间中带误差的修改的 Ishikawa迭代程序〔J〕. 数学学报, 2004, 47(2):19-228. 〔4〕张树义, 郭新琪. 增生算子方程带误差的Noor三步迭代解与收敛率的估计〔J〕. 高等学校计算数学学报, 2012, 34(1): 69-77. 〔5〕赵美娜, 张树义, 赵亚莉. 渐近伪压缩型映象不动点的迭代逼近〔J〕. 数学的实践与认识, 2016, 46(15): 264-268. 〔6〕张树义. Φ伪压缩映象带混合型误差的迭代序列的强稳定性〔J〕. 数学的实践与认识, 2005, 35(3): 185-188. 〔7〕张树义, 万美玲, 李丹. 渐近伪压缩型映象迭代序列的强收敛定理〔J〕. 江南大学学报(自然科学版), 2014, 13(6): 726-730. 〔8〕张树义, 赵美娜, 李丹. 渐近半压缩映象具混合型误差的迭代收敛性〔J〕. 北华大学学报(自然科学版), 2015, 16(3): 165-169. 〔9〕万美玲, 张树义, 郑晓迪.赋范线性空间中φ-强增生算子方程解的迭代收敛性〔J〕. 北华大学学报(自然科学版), 2016,17(3): 305-307. 〔10〕谷峰. 两个有限族一致Lipschitz映象的平行迭代算法的强收敛定理〔J〕. 数学学报, 2010, 53(6): 1209-1216. 〔11〕张树义, 林媛.Φ-φ-型压缩映象不动点的存在性〔J〕. 北华大学学报(自然科学版), 2016, 17(1): 1-3. 〔12〕张树义, 赵美娜, 刘冬红. 弱相容映射的几个新的公共不动点定理〔J〕. 江南大学学报(自然科学版), 2015,14(6): 852-856. 〔13〕张树义, 宋晓光, 栾丹. Φ压缩映象的公共不动点定理〔J〕. 北华大学学报(自然科学版), 2014, 15(2): 167-173. 〔14〕刘冬红, 张树义, 郑晓迪. 2-距离空间中一类压缩型映象的不动点定理〔J〕. 南通大学学报(自然科学版), 2016, 15(2): 68-74. 〔15〕赵美娜, 张树义. 关于2-渐近正则映象的一个注记〔J〕. 鲁东大学学报(自然科学版), 2016, 32(3): 193-197. 〔16〕张树义, 赵美娜, 李丹. 关于平方型Altman映象的公共不动点定理〔J〕. 江南大学学报(自然科学版), 2015, 14(4): 472-477. 〔17〕张树义. 赋范线性空间中渐近拟伪压缩型映象不动点的修改的广义Ishikawa迭代逼近〔J〕. 应用数学学报, 2011,34(5): 886-894. 〔18〕张树义. 一致Lipschitz渐近φi型拟伪压缩映象多步平行迭代算法的收敛性〔J〕. 系统科学与数学, 2013, 33(11): 1233-1242. 〔19〕赵美娜, 张树义, 赵亚莉. Banach空间中k-次增生算子方程解的迭代逼近〔J〕. 北华大学学报(自然科学版), 2015, 16(6): 710-714. 〔20〕张树义,李丹. 广义一致Lipschitz渐近伪压缩型映象的迭代逼近〔J〕. 渤海大学学报(自然科学版), 2015, 36(4): 294-297. 〔21〕张树义, 刘冬红, 李丹.k-次增生算子方程的迭代解〔J〕. 北华大学学报(自然科学版), 2015,16(5): 574-578. 〔22〕张树义, 宋晓光, 万美玲. 非Lipschitz渐近伪压缩映象不动点的迭代逼近〔J〕. 北华大学学报(自然科学版), 2014, 15(5): 581-587. 〔23〕张树义, 刘平.Φ-强增生算子方程的迭代解〔J〕. 渤海大学学报(自然科学版), 2008,29(3): 228-233. Convergence of Noor three step iterative sequences for asymptotically pseudocontractive type mappings ZHANG Shu-yi, LIU Dong-hong, CONG Pei-gen (College of Mathematics and Physics,Bohai University,Jinzhou 121013, China) asymptoticallypseudocontractivetypemappings;asymptoticallynonexpansivemappings;mixederrors;Noorthreestepiterativesequences 2016-10-13. 国家自然科学基金项目(No: 11371070). 张树义(1960-), 男,教授, 主要从事非线性算子迭代逼近理论, 变分不等式与优化理论方面的研究. jzzhangshuyi@126.com. O177.91 A 1673-0569(2016)04-0293-06
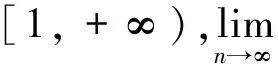
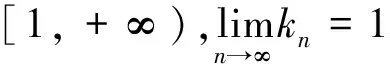
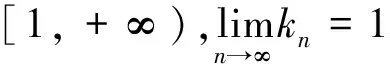
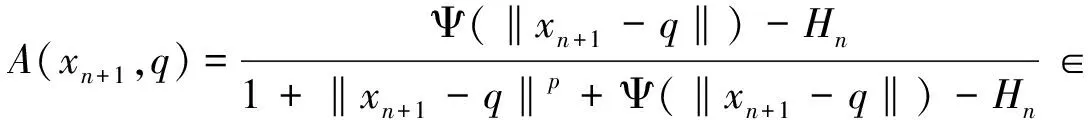
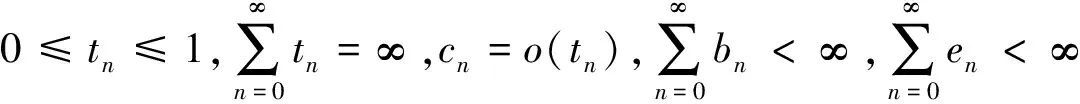
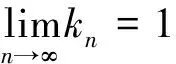
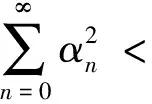
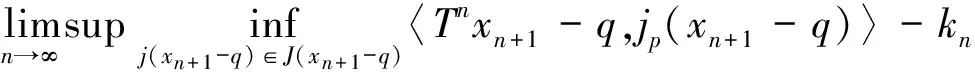
1 主要结果