单摆法测量空气密度实验分析

李明标，陈维石，孙 爽，舒天爽

(渤海大学 数理学院，辽宁 锦州 121013)



单摆法测量空气密度实验分析

李明标*，陈维石，孙 爽，舒天爽

(渤海大学 数理学院，辽宁 锦州 121013)

考虑空气浮力对单摆运动的影响，从单摆运动方程出发，计算得出振动周期与空气密度的关系，通过测量两个不同密度摆球单摆的相关物理量，求出空气密度，并分析了空气浮力对测量重力加速度的影响.

单摆；周期；空气密度；重力加速度

0 引言

空气密度是物理实验中测量的最基本物理量之一，从实验原理上多采用直接测量方法〔1〕.用天平称出某一容器充有空气和抽掉空气后的质量差，除以容量所得的商即为空气的密度.现有的实验中，大多是采用先测量空气的质量，利用水填充容器，通过测量水的质量，计算容器(空气)的体积，再由物质密度的公式计算空气密度.这种方法存在许多问题，如：抽气时容器真空程度对空气质量的影响；抽气后容器真空测量时的密封问题；测量体积时对玻璃容器充水，去水后的干燥程度，都会影响实验准确性；在实验过程上也较为繁琐、费时.本文利用单摆实验方法，在分析单摆的运动过程中，考虑空气对摆球的浮力作用，写出单摆运动方程，求近似解.通过测量两种不同单摆的摆长、周期和摆球的密度，计算出空气密度和重力加速度，回避了对空气质量与体积的直接测量，操作简单易行，结果精确可靠.

1 实验原理：

模型：图(1)中单摆为一质量为m、半径为r、密度为ρ的小球，被质量为μ的不可伸长的均质细线悬挂于定点o，小球质心到悬点的距离为l，细线与铅垂线的夹角为θ.实验在密度为ρ0的空气中进行.

计算：单摆动能：

(1)

单摆势能：

(2)

该系统的Lagrange函数为L=T-V，在不计阻尼的情况下:

拉格朗日方程:

(3)

把L带入(3)化简得：

(4)

小振幅情况下sinθ≈θ方程(4)化为：

(5)

单摆振动周期

(6)

实验选取密度不同摆球的两个单摆，测量密度、摆长和周期：

2 实验测量

表1 摆球密度测量数据表

(2)摆长测量：摆线柔软不可伸长，长度远大于摆球直径.线长由钢卷尺测出悬点至小球下端的示值，用游标卡尺测小球直径D=2r值，摆长L=l-r，摆长L>>r，可选L在 100cm左右测量.

(3)周期测量：单摆的振动周期由多功能数字测定仪测出：将单摆自然悬于两光电感应器中间，当单摆作周期摆动时，摆锤遮挡感应器，记录时间及遮挡次数，选择50个周期为一组数据进行测量，然后取平均值.

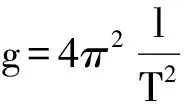
表2 单摆实验数据表

3 数据分析

表(3)中gij、ρ0ij的数据分别是考虑空气浮力通过12、23、31不同单摆组合利用(7)(8)式计算得到的空气密度和重力加速度.

表3 考虑空气浮力计算数据表

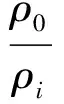
4 结论

单摆实验是大学物理实验中的最基本的实验项目，在单摆法测空气密度实验项目中，摆球密度的选取至关重要，应选取两种密度相对较小的摆球进行测量，以便能够充分反映空气浮力对单摆周期的影响，保证测量空气密度的准确性.摆球密度较大的单摆，其近似于理想单摆，空气浮力对测量结果影响不大，可较精确测量重力加速度.该实验方法原理深入浅出，设备简单耐用，实验测量方便，可作为开放实验项目，让学生分析实验原理，自主完成实验过程，提高学生学习的主动性和创造性.

〔1〕姚久民，王丽丽.空气密度与气体普适常量测量实验的改进〔J〕. 物理实验, 2011, 31(12): 24-26.

〔2〕黄兆梁.单摆周期公式的综合修正〔J〕.常州工学院学报, 2014, 27(3): 43-47.

〔3〕盛虹.单摆测重力加速度的研究〔J〕. 延安大学学报, 2014, 33(2): 28-30.

〔4〕黄焱，何松林.用单摆测空气密度〔J〕.实验室研究与探索, 2010, 29(2): 35-36.

〔5〕薛德胜,周钊,高美珍. 单摆近似周期的新形成式及构造分析〔J〕. 大学物理, 2010, 29(8): 25-27.

Theexperimentalanalysisofairdensityusingsimplependulum

LI Ming-biao, CHEN Wei-shi, SUN Shuang, SHU Tian-shuang

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

According to the motion equation of simple pendulum, considering the air buoyancy impacting simple pendulum motion, we calculate the relationship between vibration period and air density. By measuring the relevant physical quantities of two different density pendulum balls, we derive air density, and analyze the air buoyancy impacting measuring acceleration of gravity.

single pendulum；period；air density；acceleration of gravity

2016-08-13.

辽宁省教育厅教学改革项目(辽教发[2015]206号).

李明标(1965-)，男，副教授，主要从事物理实验教学与研究．

li_mingbiao@163.com.

O313

A

1673-0569(2016)04-0322-04