借动量守恒之道,破碰撞问题谜团
许志刚●
江苏省如皋市第一中学(226500)
借动量守恒之道,破碰撞问题谜团
许志刚●
江苏省如皋市第一中学(226500)
动量守恒定律是自然界中最普遍的定律,虽说其源于牛顿定律,但是其适用性比牛顿定律还要广泛,在高考中也是必不可少的内容.碰撞问题由于其涉及到动量与能量等多方面的相关知识,对于学生的综合解题能力存在有效的检验,故成为高考的热点题型.
弹性;非弹性;完全非弹性;动量守恒
在高中的学习中遇到的问题,由于碰撞过程中相互作用时间极短相互作用力又极大,故可忽略系统所受的外力,进而认为只有内力相互作用,满足动量守恒的条件.本文中针对三种不同的碰撞情况分别举例分析作答,让学生更好的体会动量守恒定律的应用.
一、弹性碰撞
又被称为完全弹性碰撞,即物体之间发生碰撞时,不存在机械能的损失,只是通过弹力做功使机械能在两物体间转移,碰撞前后物体的动量以及系统的机械能均守恒.列式关系为碰撞前后动量守恒,动能不变.
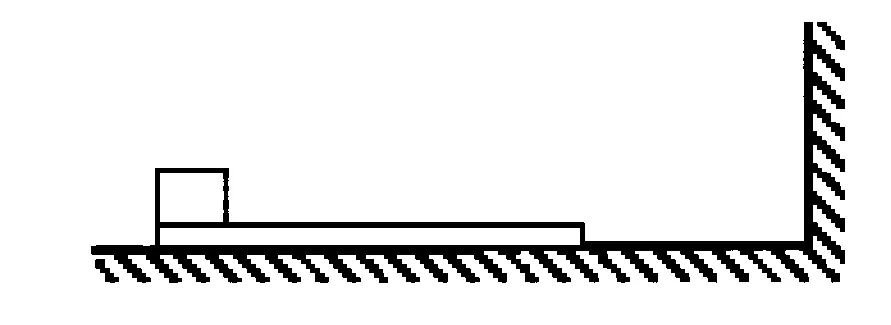
图1
例 如图1所示,有一木板左端放有一重物在光滑的水平地面上,其右方有一竖直的墙.木板质量为重物质量的1/2,重物与木板间的动摩擦因数为μ,若木板与重物速度v0共同向右运动,某时刻木板与墙发生碰撞时间极短的弹性碰撞.求木板从第一次与墙碰撞到再次碰撞所经历的时间.(设木板足够长,重力加速度为g)
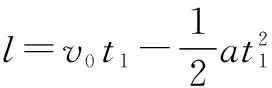
本题中的技巧性在于应用动量守恒定律求出两者达到的共同速度的大小及方向,省略了复杂的中间过程,若是运用运动学中的式子进行计算会极大地增加计算量.充分利用弹性碰撞中速度大小不变这一规律可以帮助我们快速解题.
二、完全非弹性碰撞
从能量的角度进行分析是机械能不守恒,且机械能损失最大,但动量守恒.对应此种情况的就是碰撞后碰撞物体粘在一起具有共同速度,将此过程中损失的机械能转化为物体内能.我们要借助动量守恒这一点求得碰撞后的共同速度,进而解题.
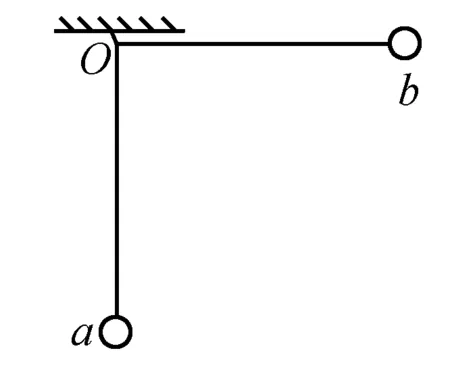
图2
例 如图2所示,点O处用等长的细线悬挂小球a、b.现让球a静止下垂,将球b向右拉至细线水平.后静止释放球b且两球碰后粘在一起向左摆动至细线与竖直方向为60°的最大偏角处.此过程忽略空气阻力,求(1)a、b两球的质量之比(2)两球在碰撞过程中损失的机械能与碰前b的最大动能之比.(设重力加速度为g)
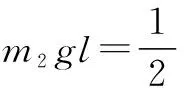
本题中对于能量的考察是创新之处,通过动量问题与能量问题的综合检验使本题更具逻辑性以及趣味性,在此类碰撞问题中必然存在能量的转换,学生必须全面掌握物理学知识才能更好的应对多变的题型,形成更为完善的解题思路.
三、非弹性碰撞
把这种情况放在最后说明,原因是从能量的角度来看其处在上述介绍的两种情况之间,即在碰撞过程中使部分机械能装化为内能,但系统的动量仍然守恒,针对此种情况,常出现要求对碰撞物的质量、碰撞后的速度等值进行范围的计算.
例 质量为1kg的小球以4m/s的速度与质量为2kg的静止小球发生非弹性碰撞,则关于碰后两球的速度v1′与v2′的取值范围是____.
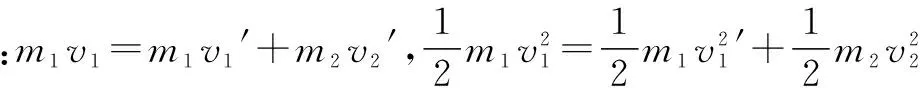
任何一种碰撞,必介于弹性碰撞与完全非弹性碰撞之间,我们只要牢记这一点,对于此类问题的求解就很简便了,本题就是借此进行对问题的分析求解.
碰撞的情况只有这三种,对于不同情况下动量守恒的运用需要选对物体以及碰撞后的运动状态,选取的对象不同必然导致所列的方程不同.灵活的运用动量守恒可以使我们的解题思路更为清晰,计算量大为减小,在碰撞问题的海洋中任意遨游.
G632
B
1008-0333(2016)34-0068-01
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

