两个解析几何新题的命题立意及教学导向分析

杨苍洲●

福建省泉州第五中学(362000)

两个解析几何新题的命题立意及教学导向分析

杨苍洲●

福建省泉州第五中学(362000)

一、试题再现

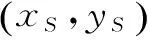
(Ⅰ)拖动点S，发现当xS=4时，yS=4，试求抛物线E的方程；

(Ⅱ)设抛物线E的顶点为A，焦点为F，构造直线SF交抛物线E于不同两点S、T，构造直线AS、AT分别交准线于M、N两点，构造直线MT、NS．经观察得：沿着抛物线E，无论怎样拖动点S，恒有MT∥NS.请你证明这一结论．

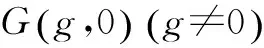
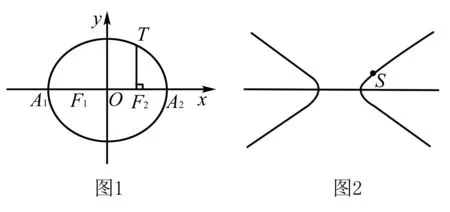
(Ⅰ)求椭圆E的方程；

(Ⅱ)给出命题：“已知P是椭圆E上异于A1,A2的一点，直线A1P，A2P分别交直线l：x=t(t为常数)于不同两点M，N，点Q在直线l上. 若直线PQ与椭圆E有且只有一个公共点P，则Q为线段MN的中点”，写出此命题的逆命题，判断你所写出的命题的真假，并加以证明;

(Ⅲ)试研究(Ⅱ)的结论，根据你的研究心得，在图2中作出与该双曲线有且只有一个公共点S的直线m，并写出作图步骤.

(注意：所作的直线不能与双曲线的渐近线平行.)

二、命题立意

1.题1(2013年福建省质检文科22)的命题立意

题1(2013年福建省质检文科22)主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、数形结合思想等．满分14分．

第(Ⅰ)步以《几何画板》探究抛物线性质为载体，考查抛物线的方程等基础知识，考查运算求解能力，考查函数与方程思想.学生只要能掌握抛物线的方程，便能根据题设中的数量关系应用待定系数法求出抛物线的标准方程.考生可能存在的错误有：由于计算的错误导致抛物线的方程解错等.

第(Ⅱ)步以应用《几何画板》探究抛物线性质——过抛物线焦点弦的性质为载体，考查直线方程、直线与抛物线的位置关系等基础知识，考查推理论证能力、运算求解能力；考查化归与转化思想、数形结合思想、函数与方程思想.学生只要掌握直线与抛物线位置关系的一般解题方法，如“设而不解”，并借助向量等工具进行合理的转化化归，便能根据题设中的关系去证明待证的结论.考生可能存在的错误有：由于计算能力较差导致解题失败，部分学生在陌生的情景下对问题产生恐惧感，导致解题信心不足，也有部分学生由于数学阅读能力较差，出现题意理解困难，导致解题受挫.

第(Ⅲ)步以《几何画板》探究推广抛物线性质——过x轴上定点的抛物线弦的性质为载体，考查学生的合情推理能力，考查抽象概括能力、推理论证能力、应用意识和创新意识；考查特殊与一般思想、必然与或然思想.学生只要掌握合情推理的一般方法进行大胆的猜测推广，便能写出相应的推广命题.考生可能存在的错误有：由于缺少必要的知识储备，或经验不足，或缺少数学直觉思维，导致解题方向缺失，无法正确寻找解题的突破口.

2.题2(2013年福建省质检理科19)的命题立意

题2(2013年福建省质检理科19)主要考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想、特殊与一般思想等.

第(Ⅰ)步主要以椭圆为载体，考查椭圆的定义、椭圆的方程等基础知识，考查运算求解能力，考查函数与方程思想.学生只要掌握椭圆的定义、椭圆的方程，便能根据题设中数量关系采用待定系数法求出椭圆的标准方程，或者应用“定义法求轨迹”求出椭圆的方程.考生可能存在的错误有：没掌握定义法求轨迹，或椭圆的基本量a,b,c间的关系记错，或由于计算的错误等导致把椭圆的方程解错.

第(Ⅱ)步以探究椭圆的一个优美性质为载体，考查直线与椭圆的位置关系、四种命题等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想、函数与方程思想、特殊与一般思想.学生只要掌握四种命题的改写、直线与椭圆位置关系的一般解题方法，直译条件即可顺利解题.解题程序为：假设P点的坐标→写出直线lA1P，lA2P的方程→写出M,N两点坐标→再写出Q点坐标→得到lPQ的方程→联立lPQ与椭圆的方程→证明Δ=0.处理好此解题程序中的每一步，即可实现命题的证明.考生可能存在的错误有：主要由于计算能力较差，或者解题信心、解题经验不足等导致解题失败.

第(Ⅲ)步以“类比探究、作图”为载体，考查学生的合情推理、作图等数学应用能力，考查抽象概括能力、推理论证能力、应用意识、创新意识，考查数形结合思想、特殊与一般思想.学生只要掌握合情推理的一般方法进行合理的类比，即可把“性质”从椭圆类比迁移到双曲线，得到相应的正确命题，并应用于作图.考生可能存在的错误有：由于知识储备不足，或经验不足，或缺少数学直觉思维，无法进行正确的类比迁移，也有部分在模式化试题下得心应手的学生，在较为新颖的试题的面前显得手足无措.

从上述两个试题的命题立意，我们可以看出，两个试题的命制均严格遵循《考试大纲》、《考试说明》的命题要求，并基于本省的教学实际.试题充分体现了 “关注交汇，注重探究，规避模式，强调应用，体现理念”的命题指导思想.同时，引导高中数学教学树立“立足基础，关注过程，突出探究，强调应用，追求‘开放’与‘多样’”的教学指导思想.

三、教学导向

上述两个试题很好地阐释了《数学课程标准》的基本理念.试题导向高中数学教学必须遵循新课程的基本理念：强调本质，注意适度形式化；倡导积极主动、用于探索的学习方式；注重提高学生的数学思维能力；发展学生的数学应用意识；体现数学的文化价值；注重信息技术与数学课程的整合.

1.强调本质，注意适度形式化

如题1(2013年福建省质检文科22)中，试题虽然以新情境“应用《几何画板》探究抛物线性质”的形式呈现，其本质依然是研究求抛物线的轨迹方程，直线与抛物线位置关系等问题.因此在下一阶段的复习中，我们要深化对圆锥曲线方程的理解，进一步熟练掌握待定系数法、定义法等求轨迹的常规方法，进一步掌握直线与抛物线位置关系的一般解题方法，要注意总结试题的规律，如：直线与圆锥曲线位置关系中的相交弦问题在高考中经常被设计成考题，在解决此类问题时，我们常联立方程组，利用韦达定理，进行“设而不解”来解题.

2.倡导积极主动、用于探索的学习方式

如题1(2013年福建省质检文科22)“几何画板”的问题情境，第(Ⅱ)问的通过观察发现，并尝试证明；第(Ⅲ)问为进一步研究抛物线性质而进行推广尝试；题2(2013年福建省质检理科19)第(Ⅱ)问探究命题是否可逆；第(Ⅲ)问通过类比推理推广命题并实际操作等.这些新颖的探究情境、设问方式，都在倡导着积极主动、用于探索的学习方式.

3.注重提高学生的数学思维能力

题1 (2013年福建省质检文科22)第(Ⅲ)步要求学生经历观察、猜测、推理、验证等思辨过程；题2(2013年福建省质检理科19)第(Ⅲ)步要求学生经历逆向思维、类比推理、操作确认的心路历程.上述两个试题都导向高中数学教学应注重提高学生的数学思维能力.数学是思维的体操，高考命题也强调以“能力立意”，因此在平时的教学时，应教给学生分析问题、解决问题的策略与方法.

4.发展学生的数学应用意识

数学是一理论性较强的基础学科.我们说，理论来源于实践，反之，理论也将指导实践.但是，在平时的教学实践中，我们却常常过分强调数学知识的理论性，而忽视了数学知识的应用性.题1(2013年福建省质检文科22)通过几何画板探究得抛物线的性质，揭示了理论来源于实践；题2(2013年福建省质检理科19)通过探究抛物线切线的作法并应用于作图，实现了用理论指导实践.两个试题完美阐释了数学知识间“理论与实践”的辩证关系.

5.体现数学的文化价值

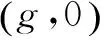
6.注重信息技术与数学课程的整合

题1 (2013年福建省质检文科22)以“几何画板探究抛物线性质”为载体进行试题的命制.题目让人眼前一亮，不得不说这是首开先河的一种试题背景，但是，究其题源，却可以说题根在课本.因为课本的阅读材料、探究发现等栏目，多次地为我们呈现了几何画板这一作图工具，并作了利用几何画板探究圆锥曲线性质的示例.通过几何画板等作图工具，必将有利于数学探究活动走向深入，有利于学生认识数学的本质.因此，通过本题，将导向高中数学教学进一步地加强数学与信息技术的结合.

G632

B

1008-0333(2016)34-0011-02