基于最短时间的车辆应急疏散模型

王 丹, 李佳洋, 李菲菲

(1. 沈阳大学 a 装备制造综合自动化重点实验室, b 信息工程学院, 辽宁 沈阳 110044; 2. 吉林城市职业技术学院, 吉林 长春 130014)



基于最短时间的车辆应急疏散模型

王 丹1a, 李佳洋1b, 李菲菲2

(1. 沈阳大学 a 装备制造综合自动化重点实验室, b 信息工程学院, 辽宁 沈阳 110044; 2. 吉林城市职业技术学院, 吉林 长春 130014)

为了应对城市大型活动中产生大量的车流在短时内迅速有效的疏散问题,提出一种合理且有效的车辆应急疏散模型.在分析应急疏散条件下车流量及其特征的基础上,对大型活动举办地相邻区域的路网进行规划,通过实地数据调查,利用遗传和蚁群混合算法,构建疏散路网选择模型.最后以沈阳市奥体中心为例对文中算法进行仿真及分析,验证该算法的有效性和可行性.

大型活动; 应急疏散; 交通模型; 遗传算法; 蚁群算法

随着人们的物质生活水平和人文素养的日益改善,对运动会、音乐会等大型活动的举办有了更多的需求.大型活动是有较高的社会认可度和群众参与度的公共活动,因其时间和地点的固定性,可以让不同城市甚至不同国家之间的人员和物质进行交流.大型活动的成功举办不仅可以丰富当地人民的生活,宣传和体现城市形象,还可以促进地方经济的快速发展,创造有利的经济效益.但与此同时,大型活动的举行也会为城市带来一些问题,尤为显著的是大型活动造成的交通问题.由于该类活动易造成短时间内的交通流的产生和吸引,引发举办地周边地区的交通拥挤.若是无法及时进行交通疏散,甚至会引起城市交通的瘫痪,不仅会给活动地周围居民的生活和出行带来不便,也会给本来已经紧张的城市交通带来更大的负担[1].

目前,国内外对于应急疏散问题的研究内容主要有交通应急疏散的交通组织管理、应急疏散方案的研究、路径选择、交通的分配等,针对具体活动制定相应的交通组织方案、应急预案,并在此基础上提出了一系列大型活动突发事件情况下的交通管理方案和措施,这些研究都取得了一定的成果[2-5].

从20世纪70年代起,国外就已经开始针对应急疏散问题进行了研究,后来伴随着越来越多突发事件的发生及其带来的严重影响,更多的研究者加入深入研究应急疏散问题的队伍.尤其在美国“9·11”恐怖袭击事件以后,应急疏散问题研究的重要意义被越来越多的国家所认识.随着经济高速发展,车辆应急疏散在应急疏散交通组织中的地位日益上升,疏散路径的选择作为车辆应急疏散的核心问题,成为首要的研究对象.如何合理地进行路径选择和优化,使交通流能够迅速被疏散到安全区域,对应急疏散问题有着重要意义.目前国内外关于应急疏散路径规划模型和交通流量的研究有很多.陈岳明等运用Pontryagin最小值定理来获得模型最优解,采用动态交通分配方法进行应急疏散路径规划[6].Mahmassani运用动态交通分配模型选择疏散路径,并给出了不同的信息供应策略在不同的用户行为下的响应规则[7].Lu等人提出一个启发式算法,即具有能力约束的路径规划算法,并给出了疏散规划问题的次优解[8].Grange等建立一个宏观的模型,利用链路密度代替链路流来估计道路的拥塞情况[9].

本文以沈阳奥体中心为例,首先对奥体中心周围路网进行规划,根据大型活动下应急疏散交通的特点,在确定应急疏散安全点的基础上,建立了基于时间最短的疏散区域各个道路到达安全点的车辆应急疏散的优化路径模型.在求解模型时,主要是在遗传算法的基础上,加入了蚁群算法的研究,规避了遗传算法的局限性,可以明显减少车辆疏散时间、提高车辆的疏散效率.通过对适应度函数进行优化、信息素的转换、选择和变异等操作,采用动态交通分配法对车辆应急疏散的路径进行优化选择.最后通过MATLAB软件进行代码编写将输出结果进行对比、分析,验证算法的可行性和优化效果.

1 车辆应急疏散模型

如果所有疏散对象都选择最短路径到达目的地,也会造成某些道路的拥堵,使交通流在疏散时出现时空分布不均.因此,为了避免上述基于路径最短的车辆应急疏散模型的弊端,为实际疏散过程寻找更优的疏散方案.选择运用基于最短时间的车辆应急疏散模型.

1.1 模型介绍

基于最短时间的车辆应急模型适用于大规模或者超大规模应急疏散,该模型不会单一地对疏散对象进行疏散,而是结合各方面的因素通过达到整体疏散过程的优化,更加具有实际研究意义.基于最短时间应急疏散模型是以疏散时间作为总体优化目标,通过疏散路径的优化,降低车辆在疏散道路上的滞留,以最快的速度使疏散对象离开疏散区域,以此实现总体疏散时间最短的目的.该模型通过考虑疏散者的撤离速度会随着道路网络的负荷不断改变的情形,制定动态的疏散方案,有助于提高疏散方案的可行性与有效性.

1.2 模型的建立

基于最短时间的应急疏散模型兼顾了疏散路径和疏散速度,该模型通过对路网中各时刻的疏散对象数量进行优化控制而达到缩短疏散时间的目的.疏散时间的指标有很多,本文所提到的疏散时间是指从第一个疏散对象进入疏散路网,直到最后一个疏散对象到达疏散目的地的整个疏散过程的全部时间.

以整个疏散过程总疏散时间最小作为目标函数的基于最短时间的车辆应急疏散模型如下:

(1)

满足

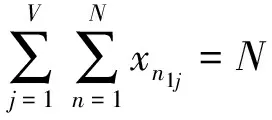
(2)

(3)

(4)

(5)

式中,vnij为对象n通过道路(Vi,Vj)时的速度,N为所有疏散道路总数,Nj为可到达第j个目的地的道路总数,V为总节点数,q为目的地的个数,kj为第j个目的地.式(1)为目标函数公式,意味着该应急疏散目标是所有疏散对象完全从疏散区被疏散的整个过程用时最短;式(2)为约束条件;式(3)意味着每个应急疏散对象最终都会到达安全目的地;式(4)、式(5)为交通流量守恒公式,即每进入疏散路径一辆车就会有一辆车从该路径驶离.式(6)为决策变量.另外,针对疏散对象在道路上的行驶速度,通常有两种方法确定,即线性拥堵模型和指数拥堵模型,如式(7)、式(8)[3].本文并未针对用度系数做详细的研究.

① 当采用线性拥堵模型时:

(7)

② 当采用指数拥堵模型时:

(8)

式中,voij为车辆在道路(Vi,Vj)的最大时速,即车辆在该条道路的限速;Cij为道路(Vi,Vj)最大的车容量;mnij为疏散对象n通过道路(Vi,Vj)时,道路(Vi,Vj)中已有车辆数;β和γ为指数拥堵模型中用来描述出行规律分布的规模和形态参数,其具体计算公式为:

(9)

(10)

其中a和b分别表示该路段上的车辆密度.

2 蚁群遗传混合算法

2.1 蚁群遗传混合算法的设计

由于车辆应急疏散模型本身需要考虑多方面因素,约束条件多、复杂度大,寻求路径最优解的过程繁琐.所以在设计算法时,基于遗传算法适用性广泛的特点,首先考虑采用遗传算法.但是,由于传统的遗传算法容易过早地收敛从而导致局部最优,影响全局最优的求解,且在疏散问题规模较大时,搜索的时间也会被延长.因此本文针对上述原因,考虑在传统遗传算法的操作上,加入蚁群算法,将两种算法进行结合以期望提高求解的质量和效率.

(1) 适应度函数的确立.在算法设计的早期阶段,为了避免算法过早收敛,需要根据适应度的大小对个体进行选择,为了增加求解的准确性,需要对适应度函数进行定义,使种群中的个体在被下一代选择时的概率能够相似,使优秀个体被选中的概率逐渐增大[10-11].因此,可采取如下动态控制的适应度函数.

(11)

(2) 信息素的迭代.当利用遗传算法求出最优解后,需要对得到的优化路径做信息素的转化,该操作相当于蚁群算法中对全局信息素进行更新.当疏散方向较多时,利用遗传算法得出的优化路径集相对集中时,使得信息素在路径上分到的浓度不够,进而影响后期蚁群算法的求解速度.针对上述问题,考虑引入相当于局部信息素更新的更新策略:在遗传算法每次迭代后,针对种群中的优化路径进行信息素转化,达到加速较好路径上信息素分布的效果.假设遗传算法每次迭代产生K组路径,更新机制.

(15)

式中:ρGA为残留因子0≤ρGA<1,1-ρGA为信息素的挥发程度;ω为自定义系数;NCGA为遗传算法计算过程中迭代次数.

(3) 选择操作.本文的选择操作由适应度值和信息素含量共同确定,即个体被选择的概率Pi如下所示:

(16)

式中,n为路径的条数,k为信息素的重要因子,λ为适应度的重要因子,Fi为第i条路径的适应度值.

(4) 交叉变异点的选择.在遗传算法中进行交叉、变异等操作时,所参与的基因一般是随机选择的.这样做虽然可以加强全局搜索能力,但也增加了算法的无效操作次数.所以需要对进行交叉变异的基因进行选择,增加了较长边及信息素含量较少的边作为交叉变异位置的概率.为此,本文利用节点i和节点 j之间的信息素含量及其形成的边s的长度建立如下的选择机制:

(17)

其中,ds为边s的长度;θ 、δ为两个参数,分别反映边 s上的信息素和长度在交叉变异点选择中的相对重要性.

2.2 遗传蚁群算法流程

遗传蚁群算法的基本流程的步骤如下:

步骤1 定义问题的目标函数和适应度函数;

步骤2 利用遗传算法产生优化解;

步骤3 将遗传算法产生的优化解,通过信息素转化策略转化为初始信息素;

步骤4 将蚁群算法各参数初始化,把M只蚂蚁随机地置于N个结点;

步骤5 依次选择节点进行遍历直至将N个节点全部遍历,形成一条路径;

步骤6 计算各路径的适应度及信息素含量,并进行选择操作;判断是否满足终止条件,若不满足则继续执行步骤 7,若满足则跳过剩余步骤直接执行步骤10;

步骤7 对M路径依次进行交叉、变异操作;

步骤8 此时共有M+U(U≤M)条路径,根据适应度及信息素对M+U条路径进行排序,选出前M条路径;

步骤9 对信息素进行更新,转步骤5;

步骤10 得到全局最优路径,停止循环.

3 仿真数据及分析

3.1 仿真数据及背景

沈阳奥林匹克体育中心分为“一场三馆”,其中“一场”是指五里河体育场;“三馆”分别为体育馆、游泳馆和网球馆.体育场周边共设立了15处停车场,分别可供社会车辆、公交车、体育赛事工作车辆、出租车、摩托车及非机动车辆停靠,共能提供8 150个停车位.体育场内设置了450个停车位,其中,体育场1层环廊停车场可停放机动车238台;体育场西北侧、东北侧停车场可停放机动车212台.由于五里河体育场周边路网完整,常态下的交通流较小.因此,在大型活动举行期间,需要对周边附近路网进行交通管制可以消除背景交通对疏散的影响.本文的疏散主要针对五里河体育场的内部停车场的450辆车进行疏散.图1为奥体中心疏散路网图.

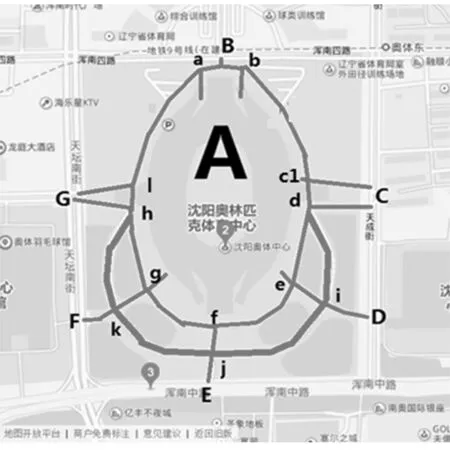
图1 沈阳奥体中心疏散图

如图1所示,以奥体中心内部停车场区域作为发生源,设为A点,共有6个疏散方向即6个疏散出口,分别为图中的B、C、D、E、F、G.

根据本次研究需要,从这6个出口中选取3个作为疏散安全点.由于B出口附近聚集各种体育馆,考虑人流量较大所以疏散点不考虑B出口.C和D出口可以使车辆到达同一条道路,所以考虑从中选取一个作为疏散安全点,由于C出口附近连接道路较多,便于车辆的后续疏散,所以选取C出口作为安全疏散点之一;E出口作为直接与浑南中路主干道相连的唯一出口,便于车辆疏散也是安全疏散点的备选之一;F和G出口链接同一条主干道,由于F出口距离浑南中路较近,容易对E出口的车辆造成滞留,所以选择G出口为安全疏散点.基于以上原因,确定安全疏散点为C、E、G.

基于相关资料关于奥体中心道路情况的实际数据,利用上述算法进行MATLAB编码,求得能够使车辆在疏散路网中的最优路径,使所有车辆尽力在最短时间内疏散至安全目的地.从事发区域A到各安全点的安全点的疏散网络如图2所示.

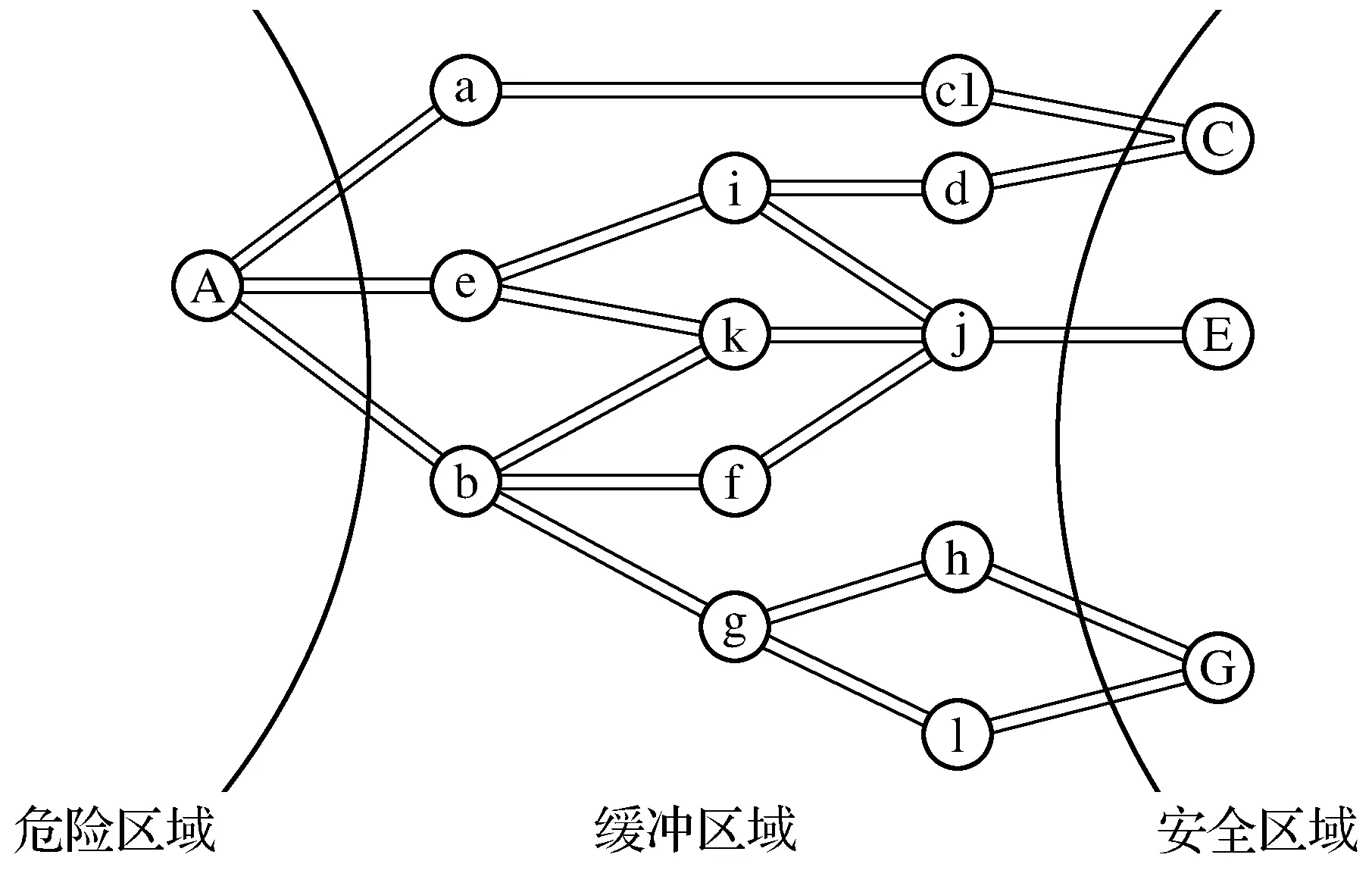
图2 疏散路网示意图

从图2可知,本次疏散共有12个节点,3个安全疏散点.根据相关资料和实际数据调查,各路段基本信息如表1.

表1 路段基本信息

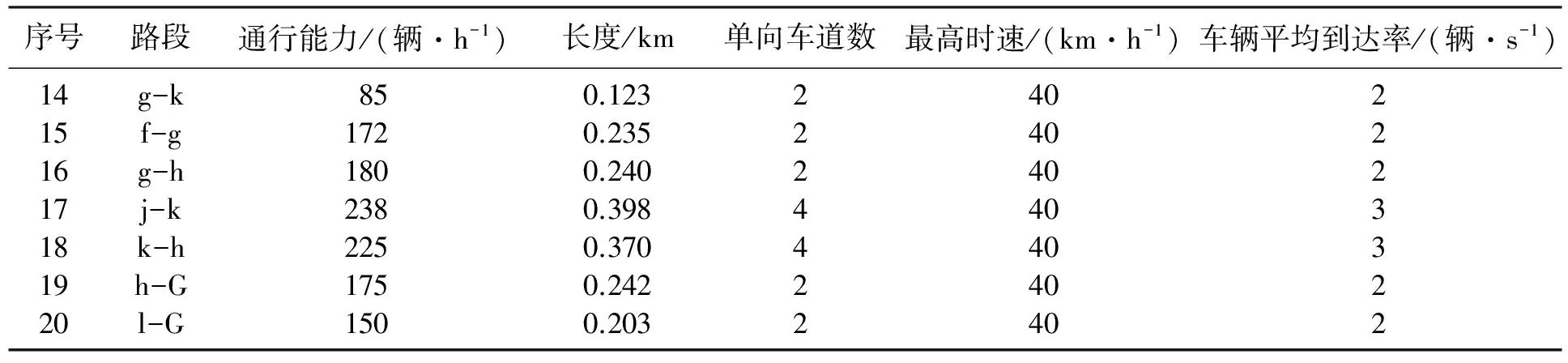
续表1

3.2 仿真结果与分析

利用各路径的基本信息,分别运用单独遗传算法和蚁群遗传混合算法进行运算,得到的优化路径及其疏散时间如表2和表3所示.

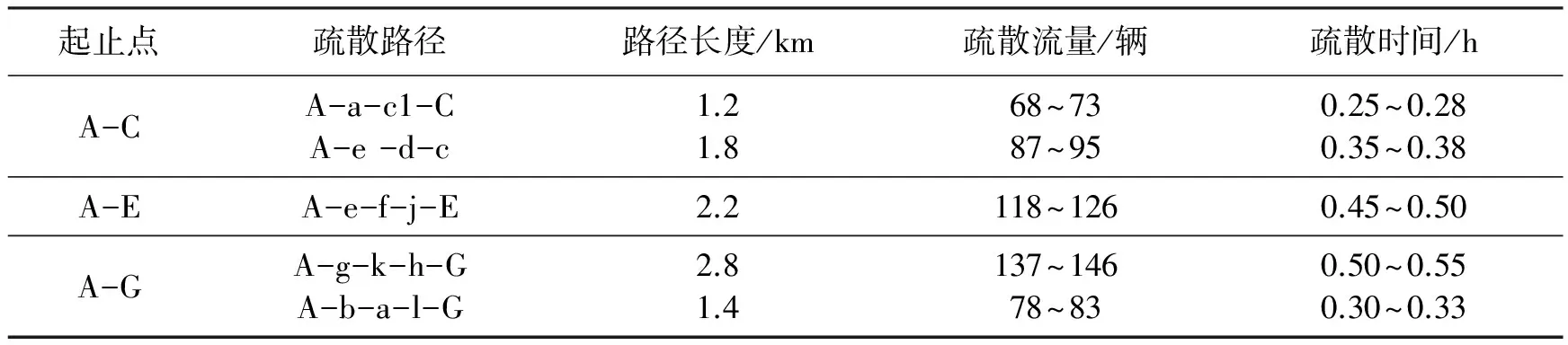
表2 遗传算法的最优疏散路径

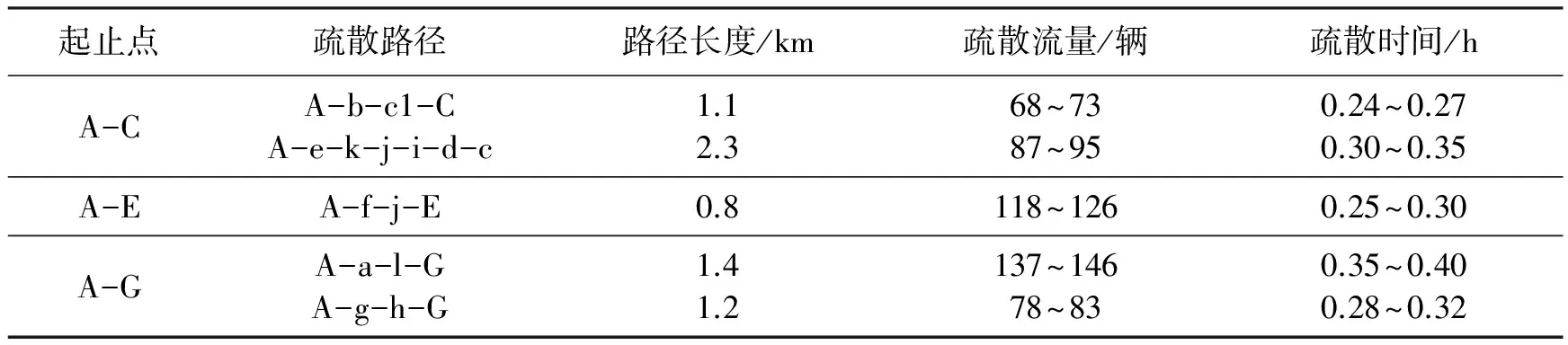
表3 蚁群遗传算法的最优疏散路径

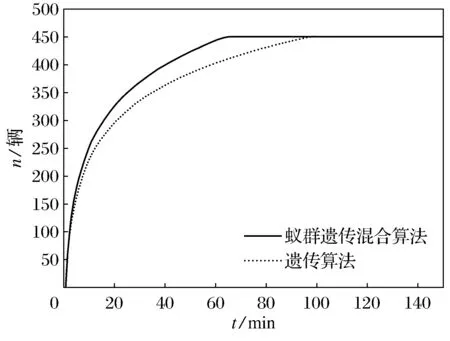
图3 疏散结果对比图

根据2.2节中的遗传蚁群算法流程,利用现有数据,运用MATLAB软件对上述两种算法进行车辆疏散仿真模拟,得到的疏散结果如图3所示.通过对比可以发现,单独运用遗传算法进行路径选择时,通过三个疏散口的车辆疏散时间明显高于蚁群遗传算法的时间.当运用遗传算法求解时,车辆完全疏散时的总疏散时间约为100 min,当运用蚁群遗传混合算法进行求解时,450辆车完全疏散的总疏散时间仅为63 min,明显优于单独的遗传算法,验证了本文中,车辆应急疏散优化算法的可行性.

4 结 论

应急疏散是意图在最短时间内将疏散对象转移至安全目的地,不但要确保人的生命安全,还要保障人的财产安全.尤其在大型活动举办时,车流和人流的短时间内集聚,车辆应急疏散对缓解交通情况发挥着重大的积极作用.本文只是基于最短时间内车辆疏散模型进行研究,并假设大型活动举办时的所有道路都是可通行的.本文未考虑司机的主观因素,而是假设他们都是愿意服从安排的,也没有考虑到道路选择时的风险评估以及车辆拥挤程度对车辆应急疏散时路径选择的影响.

[ 1 ] 杨晶. 城市大型活动应急交通疏散对策研究[D]. 大连:大连理工大学, 2011. (YANG J. Study on emergency traffic coping strategies during urban large-scaleevents[D]. Dalian: Dalian University of Technology, 2011.)

[ 2 ] 李海鹏. 城市重大突发事件下应急疏散交通流仿真研究[D].成都:西南交通大学, 2015. (LI H P. Simulationstudy on traffic flow evacuation under the urban major emergency incidents[D]. Chengdu: Southwest Jiaotong University, 2015.)

[ 3 ] 黄有波,吕淑然,杨凯. 大型办公场所火灾与应急疏散研究[J]. 消防科学与技术, 2015,14(8):24-27. (HUANG Y B, LYU S R, YANG K. Research on fire and emergency evacuation of large office building[J]. Fire Science and Technology, 2015,14(8):24-27.)

[ 4 ] 周继彪,陈红,闫彬,等. 综合交通枢纽安全应急疏散路径选择研究[J]. 中国安全科学学报, 2014,23(2):147-153. (ZHOU J B, CHEN H, YAN B, et al. Research on emergency evacuation route choice in integrated transport hub[J].China Safety Science Journal, 2014,23(2):147-153.)

[ 5 ] 王丹,李蓓蕾. 城市复杂动态交通自适应局部路由策略[J]. 沈阳大学学报(自然科学版), 2016,28(3):219-222. (WANG D, LI B L. Adaptive local routing strategy in complex urban dynamical traffic networks[J]. Journal of Shenyang University(Natural Science), 2016,28(3):219-222.)

[ 6 ] 陈岳明,萧德云. 基于动态交通分配的路网应急疏散模型[J]. 清华大学学报(自然科学版), 2009,49(8):1102-1105. (CHEN Y M, XIAO D Y. Dynamic traffic assignment-based method for real-time traffic management during emergency evacuation[J]. Journal of Tsinghua University (Natural Science), 2009,49(8):1102-1105.)

[ 7 ] MAHMASSANI H S. Dynamic network traffic assignment and simulation methodology for advanced system management applications[J]. Networks & Spatial Economics, 2001,1(3):267-292.

[ 8 ] LU Q, GEORGE B, SHEKHAR S. Capacity constrained routing algorithms for evacuation planning: a summary of results[J]. Lecture Notes in Computer Science, 2005,3633(8):291-307.

[ 9 ] GRANGE L D, GONZLEZ F, BEKHOR S. Path flow and trip matrix estimation using link flow density[J]. Networks & Spatial Economics, 2016:1-23.

[10] 杨建芳,高岩,王宏杰. 多层建筑物应急疏散模型和算法[J]. 系统仿真学报, 2014,26(2):145-149. (YANG J F, GAO Y, WANG H J. Multi-storied building emergency evacuation model and algorithm[J]. Journal of System Simulation, 2014,26(2):145-149.)

[11] 马超,郭健,阚映红,等. 基于遗传算法的应急疏散方案研究[J]. 测绘科学技术学报, 2014,29(6):78-83. (MA C, GUO J, KANG Y H, et al. The emergency evacuation schedule problem based on genetic algorithms[J]. Journal of Geomatics Science and Technology, 2014,29(6):78-83.)

【责任编辑: 李 艳】

Model of Vehicle Emergency Evacuation Based on the Shortest Time

WangDan1a,LiJiayang1b,LiFeifei2

(1. a. Key Laboratory of Manufacturing Industrial Integrated Automation, b. School of Information Engineering, Shenyang University, Shenyang 110004, China; 2. Jilin Vocational and Institute of Technology, Changchun 130014, China)

In order to solve the evacuation problem of a large amount of vehicles in a short period of time during the large-scale activities, a reasonable and effective vehicle emergency evacuation model is proposed in this paper. On the basis of analyzing the traffic flow and its characteristics under the condition of emergency evacuation, the evacuation network planning is established in the large-scale activities adjacent areas. Then using genetic and ant colony algorithm, the evacuation route choice model is constructed through the field survey data. Finally, the Shenyang Olympic Sports Center as an example, the proposed algorithm is simulated and analyzed to verify the effectiveness and feasibility of the algorithm.

large-scale activities; emergency evacuation; traffic models; genetic algorithm; ant colony algorithm

2016-06-27

国家自然科学基金青年基金资助项目(61203152); 辽宁省自然科学基金资助项目(2015020037); 辽宁省教育厅杰出青年学者成长计划资助项目(LJQ2014131); 辽宁省教育厅资助项目(L2014473).

王 丹(1979-),女,辽宁沈阳人,沈阳大学副教授,博士.

2095-5456(2016)06-0482-06

U 491

A