“管理运筹学”指派问题解法探析*
黄 毅 ,邓志英
(湖南工程学院a.管理学院;b.经济学院,湖南 湘潭 411104)
“管理运筹学”指派问题解法探析*
黄 毅a,邓志英b
(湖南工程学院a.管理学院;b.经济学院,湖南 湘潭 411104)
指派问题是管理运筹学教学过程中重要章节,匈牙利法是解决此类问题的基本方法,在教学过程中有学生提出了自己的看法和解题思路,严格按照匈牙利法基本步骤和调整之后的步骤进行了对比,结果显示学生的解法有一定的优势但也有缺陷;严格按照匈牙利法则过程复杂但不会面临选择困难,结果准确但明显速度慢于学生的方法。
管理运筹学;指派问题;匈牙利法;最优解
“管理运筹学”是一门管理科学和现代化管理方法相结合的、注重实践应用的课程。在教学实践中,一些教师习惯于教条主义,过分严谨,授课内容都是千篇一律,从定义到定理,再到证明,最后是例题讲解,这样不仅课堂缺乏生气,学生上课也除了记录就无需理解和思考,很难真正理解所学知识点,更不能灵活运用。[1]因此锻炼学生解决问题能力,开发他们创新思考解决问题的方法,将使我们的教学手段和方法得到提升,在“管理运筹学”指派问题的教学过程中我们就充分发挥学生的主观能动性,让他们主动解决问题,主动发现新的方法,以下讨论的就是在教学过程中学生发现的解题方法。
生活中经常会遇到这样的问题:有m个人恰好可以完成m项任务,一项任务由一个人完成,一个人只完成一项任务,由于对象特点与能力不尽相同,完成任务的效率和收益也不相同。[2]因此,安排适当的人完成适当的任务,获取最佳经济效益成为此类问题的关键,这类问题我们称为指派问题或分派问题。指派问题是教材“管理运筹学”一个章节,是现实世界经常遇到的问题,解决指派问题的方法是由匈牙利数学家考尼格提出的,因此称为匈牙利法。
一 匈牙利法基本思想
匈牙利法的理论根据是考尼格提出并证明了的两个定理:[3]
定理1:设一个指派问题的效益矩阵(Cij)的行(或列)的各元素中分别减去该行(或列)的最小元素后得到一个新矩阵(Bij),则以(Bij)为效益矩阵的指派问题与原问题有相同的最优解。
定理2:若一方阵中的一部分元素为0,一部分元素为非0,则覆盖方阵内所有0元的最少直线数恰好等于那些位于不同行、不同列的0元的最多个数。
二 匈牙利法基本步骤
第一,效益矩阵的初始变换——0元素获取;
第二,最优性检验;
第三,找出能覆盖非最优矩阵中所有0元素的最少直线集合;
第四,非最优矩阵变换——0元素移动。
匈牙利法针对的是标准的指派问题,即必须满足以下三个条件:
1.目标要求为min;
2.效益矩阵(Cij)为n阶方阵;
3.阵中所有元素Cij≥0,且为常数。
如果没满足以上三个条件,则必须把效益矩阵化成标准指派问题。但在本科教学过程中,我们发现解题过程中出现一系列问题在此探讨。
例如:我们安排甲、乙、丙、丁四人完成三项任务A、B、C,一个人只能做一项任务,他们完成任务的利润情况如表一所示,其中“-”表示不能胜任该项工作。

表一 四人完成任务利润
在解决此类指派问题时很多同学提出自己的看法,我们在此通过比较来回答一些同学提出的疑问,即我们首先按照匈牙利法进行求解,然后再按照一些同学提出的思路进行解答。
三 按照匈牙利法基本步骤求解
用表一中的最大元素去减表中每一个元素,然后增加一列使得原矩阵变成标准型指派问题如下:

每行每列减去每行每列中最小元素得到:

画0元素得到:

⊗表示画圈的0元素,由此可知我们没有得到最优解,必须通过画直线来寻找最优解,通过画三条直线覆盖所有0元素,然后得知没有被直线覆盖的最小元素是1,没有被直线覆盖的元素减去1,被直线十字交叉覆盖的元素加1得到新的矩阵如下:

再画0元素得到最优解:

则最优解为甲做B任务,乙做A任务,丙做C任务,总的利润是6个单位。但在给本科生教学过程中,有的学生提出如果先每行每列减去每行每列最小元素,再化标准指派问题求解,过程简单,一步就可以求到最优解,不用再画直线进行调整,可直接得到最优解。
四 匈牙利法调整之后步骤求解
用原矩阵中最大元素减矩阵中每一个元素得到如下矩阵:

每行每列减去每行每列中最小元素得到:
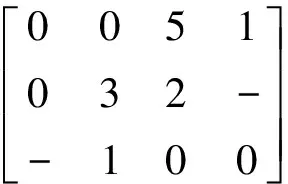
再补充一行0元素得到标准指派问题矩阵:

画0元素得到矩阵:

这时第三行和第四行都剩下两个0元素,第三列和第四列也是两个0元素,不同的选择会有不同的结果,这时我们必须回头看一下原始矩阵才能做出正确选择,原始矩阵中丙做C任务的利润是1个单位,而丁做C任务的利润是0单位,因此我们选择丙做C任务,这样我们就得到了最优矩阵如下:

五 结 语
这个最优矩阵的结果与我们完全按照匈牙利法基本步骤结果是一样的,但解题过程相对简单,不一样的地方是他必须面临选择,这种选择是必须回头看原始矩阵才能正确做出。这种方法在教学过程中被很多学生使用,且结果正确,只是在使用时都必须面临选择。如果严格按照匈牙利法的基本步骤则不会面临选择,只是可能一次性得不到最优解,要进行调整再寻找最优解。两种方法的差别在于严格按照匈牙利法是先补充一行0元素,再每行每列减每行每列最小元素;而调整之后的方法是先每行每列减每行每列最小元素,再补充一行0元素。两种方法都能得到最优解,只不过前一种方法不会面临选择,但过程复杂;后一种方法过程简单,但面临选择。我们再用两种方法分别对“管理运筹学”教材173页课后第六题进行计算,结论相同。通过在教学过程中积极引导学生思考、培养学生创新解决问题的能力,减少了学生对“管理运筹学”恐惧感和厌学情绪,调动了学生的积极性和学习热情,提升了教学效率[4]。同时,通过建立教师和学生的双向联动与引导机制进而取得了更为优良的教学效果,最终使学生准确、有效地掌握“管理运筹学”这门知识。
[1] 郭建华.高校转型发展时期经管类专业《管理运筹学》课程教学改革探索[J].教育教学论坛,2015(7):113-114.
[2] 董银红,付丽丽. 管理运筹学[M].大连:东北财经大学出版社,2014:128-141.
[3] 韩大卫. 管理运筹学[M].大连:大连理工大学出版社,2006:164-170.
[4] 李 颖. 财经类院校《管理运筹学》课程教学的改革与实践[J].教育教学论坛,2015(12):281-282.
Analysis of Assignment Problem in Managerial Operations Research
HUANG Yia,DENG Zhiyingb
(a. School of Management, b. School of Economics, Hunan Institute of Engineering, Xiangtan 411104, China)
Assignment problem is an important chapter in the teaching process of Managerial Operations Research. The Hungarian Method is the basic method to solve problems. In the process of teaching, students put forward their views and problem-solving ideas. This paper compares with the two ways between Hungarian Method and the adjusted Hungarian Method. The results show that the students' solution has certain advantages, but also has flaws. Hungary Method turns out to be a complicated proless, easy to select, but wth slow speed and exact result.
Managerial Operations Research; assignment problem; Hungarian Method; optimal solution
2016-02-26
2016年湖南省高校教学改革研究立项项目(湘教通[2016]400号,序号602);2014年湖南省教育科学规划项目(XJK014BGD016)。
黄毅(1973-),男,博士,副教授,硕士生导师,研究方向:高等教育。
G642.0
A
1671-1181(2016)04-0080-03

