基于刚柔耦合模型的变速器敲击特性*

丁 康， 陈志强， 杨志坚

(1.华南理工大学机械与汽车工程学院 广州，510641)(2.重庆理工大学汽车零部件先进制造技术教育部重点实验室 重庆，400054)



基于刚柔耦合模型的变速器敲击特性*

丁 康1,2， 陈志强1,2， 杨志坚1,2

(1.华南理工大学机械与汽车工程学院 广州，510641)(2.重庆理工大学汽车零部件先进制造技术教育部重点实验室 重庆，400054)

为研究变速器齿轮传动系统的敲击振动特性，专门设计了一台只包含两个档位的试验变速器。以该试验变速器为研究对象，综合考虑各零部件连接关系、齿轮内部动态激励、发动机转速波动和负载激励、轴承刚度阻尼特性以及箱体的柔性化特性，运用LMS virtual lab软件建立变速器的刚柔耦合多体动力学模型，分析了变速器齿轮系统敲击的产生条件并给出敲击时间历程与各影响因素的理论表达式，最后基于刚柔耦合模型对敲击各影响因素进行系统的分析研究。研究结果表明,通过合理地设计齿轮系统参数可以把敲击控制在理想范围内。

变速器； 敲击； 刚柔耦合模型； 敲击时间历程

1 问题的引出

随着汽车日益向着安全和舒适的方向发展，振动、噪声问题也随之愈发凸显，相应的法规对振动、噪声问题限制也越来越苛刻[1]。变速器齿轮系统是汽车主要的噪声源之一，掌握变速器齿轮系统的振动噪声特性，特别是变速器齿轮系统敲击振动特性，不仅可以使降噪措施有的放矢，而且可以有效地减少变速器开发的周期和成本，因此对变速器齿轮系统敲击振动特性的研究具有重大的工程实用价值。目前国内外学者对齿轮系统敲击特性的研究已经取得了众多成果，在模型建立方面，提出了考虑自由度比较少、求解快速的集中参数模型[2-3]，或者是充分考虑了每部件的局部特性以及连接特性的有限元模型[4]。集中参数模型忽略因素比较多，求解粗略；有限元模型自由度巨大，耗费大量的计算资源；而刚柔耦合模型[5-6]集合了前两种模型的优点，每个刚体包含6个自由度，同时对一些重要的部件柔性化，不仅满足了求解精度的要求，而且节省大量计算资源。笔者基于LMS virtual lab刚柔耦合建模平台对变速器的敲击振动特性进行研究。在敲击特性分析方面，目前研究较多的是离合器特性参数对齿轮敲击的影响[7]，或者只单独分析几个齿轮参数[8]、变速器运行状态等对敲击的影响[9]，很少有对敲击产生的条件、影响因素进行系统深入分析。笔者通过分析敲击产生的条件以及敲击时间历程与各影响因素的理论表达式，研究各因素对齿轮系统敲击的影响。

实际变速器的振动噪声问题主要分为啸叫和敲击两类，笔者设计一台两档位三轴式变速器，一个档位传递动力模拟变速器啸叫特性，另一档位不传递动力模拟变速器敲击特性，同时为了在研究过程中更加方便提取所需信号，两档位变速器在设计过程中忽略了一些实际变速器机构，例如换挡机构。以图1所示的两档位三轴式试验变速器为研究对象，综合考虑齿轮系统的内部激励、外部激励以及轴承的刚度阻尼特性，运用刚柔耦合方法建立变速器振动预测模型，并分析变速器齿轮系统敲击的产生条件以及敲击时间历程与各影响因素的理论表达式，最后对各影响因素进行全面研究。

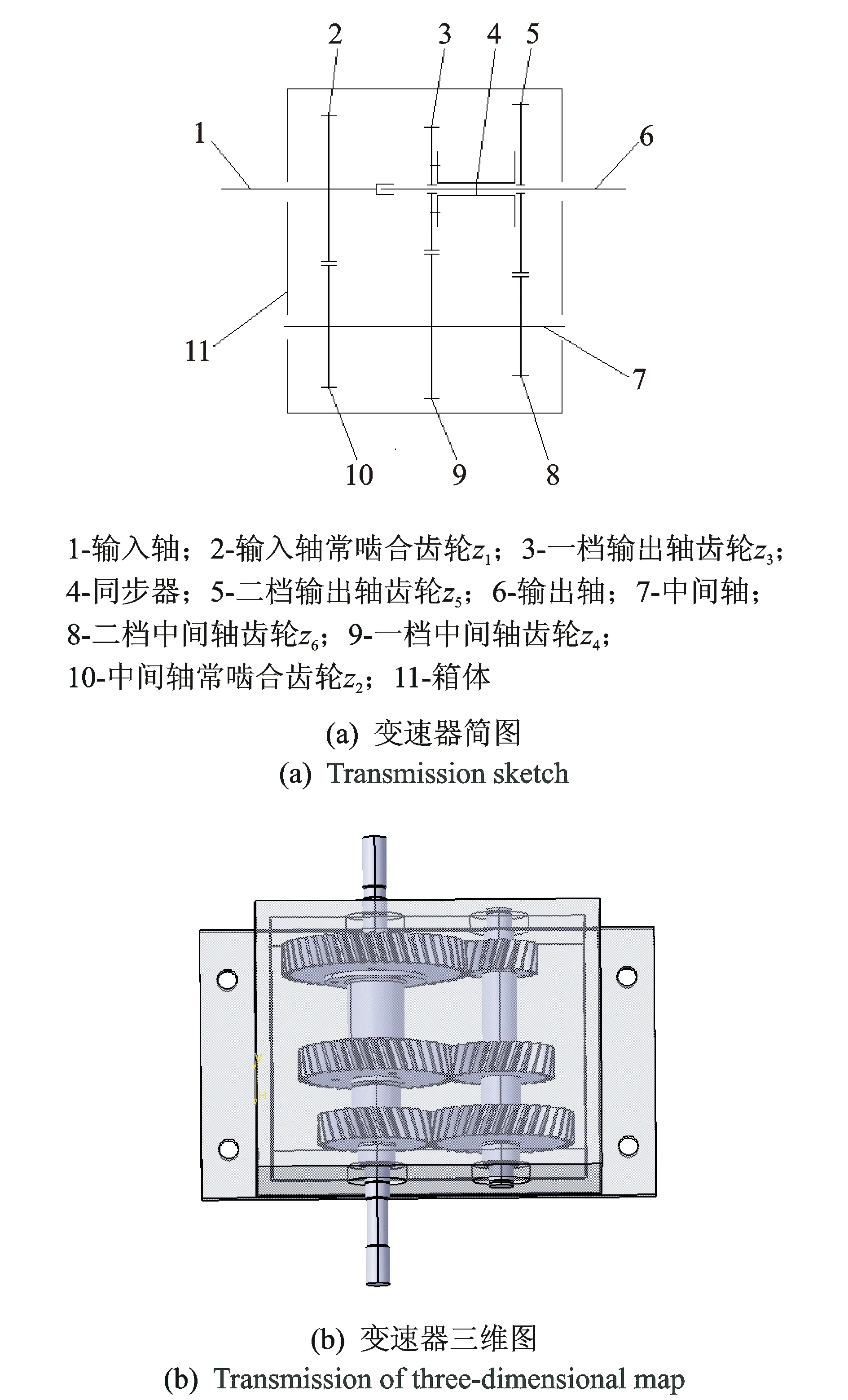
图1 试验变速器Fig.1 Test transmission

2 变速器刚柔耦合多体动力学模型

2.1 变速器多体动力学模型

利用LMS virtual lab软件根据齿轮、轴、轴承、箱体之间的实际连接关系以及材料属性建立整个变速器的多体动力学模型，例如齿轮对之间添加齿轮接触副模拟齿轮之间啮合力、传动轴与箱体之间添加bush衬套模拟轴承特性、输入轴与输出轴之间添加圆柱副(即可绕轴向相互转动又可相互平动)等，各零件之间的连接副如表1所示。

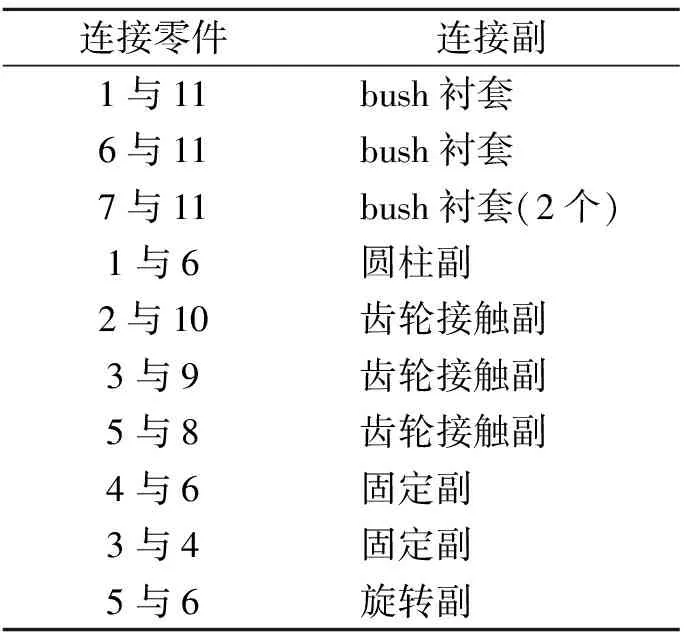
表1 各零件间连接关系

2.2 箱体柔性化

为准确获得箱体表面的振动信号，在建立变速器的多体动力学模型后，有必要对变速器箱体进行柔性化处理。利用Hypermesh软件对箱体进行网格划分，为了验证所建立的有限元模型的准确性，分别对箱体进行了有限元自由模态分析和试验自由模态分析，对比前10阶结果如表2所示。结果表明，理论值与试验值误差在3%以内，基本吻合。接着采用Nastran求解器获取Craig Bampton[10]模态结果，在LMS virtual lab中将箱体刚体模型柔性化，箱体柔性化的变速器模型如图2所示。

表2 变速箱箱体前10阶模态频率

图2 变速器刚柔耦合多体动力学模型Fig.2 Transmission rigid-flexible coupling multi-body dynamics model

2.3 动态激励模拟

2.3.1 齿轮啮合力

综合考虑齿轮时变刚度、阻尼、动态传递误差和齿侧间隙的影响，齿轮的啮合力[11]为

(1)

其中：x(t)=r1θ1-r2θ2为啮合齿轮对动态传递误差；r1,r2,θ1,θ2分别为啮合齿轮对齿轮1和齿轮2的基圆半径和扭转振动位移；v12为两齿轮扭转振动相对速度；km(t)为齿轮啮合时变刚度；cm为齿轮啮合阻尼，它是随负载和速度变化的时变参数。

km(t)计算公式由参考文献[12]给出,其核心思想是采用傅里叶级数展开式近似表示齿轮啮合刚度的时变性。

对cm进行简化，将按CAI方法[12]计算得到的平均啮合刚度代入啮合阻尼的计算公式中，取其结果作为啮合阻尼的值，计算公式[13]为

(2)

其中：I1,I2分别为齿轮1和齿轮2的转动惯量；ζg为齿轮的啮合阻尼比。

根据R. Kasuba[14]分析计算结果，啮合阻尼比一般取值为0.03～0.17，本研究取0.1。

f(x(t))为齿轮间隙非线性函数，如式(3)所示，间隙b取0.02 mm，图3为主动齿轮位于齿轮间隙中间位置的示意图。齿轮相对位移0.01 mm与-0.01 mm都代表了主动齿轮位于齿轮间隙的中间位置，正负号只是说明了两齿轮的相对运动方向不同。当主动齿轮由图示位置从B侧向被动齿轮A侧运动时，相对位移由-0.01 mm向+0 mm(+0表示主动齿轮B侧与被动齿轮A侧刚好接触)变化，当B与A接触后，继续相对A往图示左侧运动，则此时发生接触变形，相对位移为正值；当主动齿轮由图示位置从C侧向被动齿轮D侧运动时，相对位移由0.01 mm向-0 mm(-0表示主动齿轮C侧与被动齿轮D侧刚好接触)变化，当C与D接触后，继续相对D往图示右侧运动，则此时发生接触变形，相对位移为负值。

(3)

图3 齿侧间隙图Fig.3 Gear backlash

2.3.2 发动机转速波动模拟

为了模拟实际发动机转速的波动对变速器的影响，试验变速器的输入转速激励可按式(4)控制

(4)

2.4 轴承刚度阻尼特性

齿轮啮合产生的振动通过轴承传递到变速器箱体，轴承的刚度阻尼特性对预测齿轮系统的振动噪声极其重要。模型中轴承通过添加bush衬套模拟，刚度阻尼值参考文献[15]的方法基于Hertz接触理论和EHL弹流润滑理论推导得到，该方法得到的刚度阻尼值充分考虑了轴承内部几何结构、润滑特性以及轴承刚度阻尼随转速和负载变化的特性。

3 变速器敲击特性

3.1 敲击产生条件

一般来说，在汽车变速器中，空套齿轮比承载齿轮更容易产生敲击，同时空套齿轮也是最主要的敲击噪声源，因此本研究只针对空套齿轮z5z6的敲击现象进行研究。由传动关系分析可知，z6为主动齿轮，z5为被动齿轮，对齿轮z5受力分析，如图4所示。规定逆时针方向为正值，根据牛顿第二定律，被动齿轮z5的平衡条件为

(5)

图4 齿轮z5受力分析Fig.4 Gear z5 stress analysis

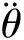
为了更直观表达敲击历程和定量表述敲击条件，定义敲击时间历程β(t)[11]为

(6)

因此敲击产生的条件可以表示为

(7)

3.2 敲击影响因素分析

对被动齿轮z5进一步受力分析可知，被动齿轮z5所受的阻滞力矩主要是由齿轮与传动轴之间的阻尼产生，即阻滞力矩为

(8)

由式(4)和齿轮运动传递关系可得

(9)

式(6)敲击时间历程可以进一步表示为

(10)

图5 转速波动20 r/min时的敲击情况图Fig.5 Rattle case of the speed fluctuation is equal to 20 r/min

当转速波动为20 r/min时，从图5(a)中可看出，齿轮z5与z6始终在AB侧(如图3所示)啮合(齿轮相对位移一直大于0 mm)，齿轮啮合力主要由齿轮之间相对位移即齿轮之间的微小变形产生，在此微小变形情况下齿轮啮合力与相对位移几乎成比例关系，齿轮z5与z6啮合正常。图5(b)齿轮敲击时间历程一直处于-1与1之间，也说明了齿轮对z5z6之间没敲击现象发生。由于空套齿轮处于正常的啮合状态，所以图5(c)变速器箱体测点1处的振动信号频率成分比较简单，图中标出了负载齿轮对z1z2与z3z4的第1阶啮合频率(540 Hz和387.5Hz)，负载齿轮对z1z2第5阶啮合频率(2 700Hz)由于与箱体的固有频率接近因而幅值比第1阶增大很多。此外，由于输入轴转速波动，在啮合频率附近也出现了传动轴的调制频率成分。

当转速波动为25r/min时，从图6(a)中可看出，齿轮z5与z6在AB侧发生了单侧敲击(齿轮相对位移由-1.5×10-3mm向+0mm变化)，开始时齿轮z6由A侧向z5的B侧运动，这段时间内齿轮之间没接触，齿轮啮合力为0。当两齿轮相对位移大于0，则两齿轮在AB侧发生了敲击，齿轮啮合力瞬间增大，但两齿轮此时没有立即分离，而是在啮合处发生微小变形并伴随着轻微的敲击，最后两齿轮分离进入下一次单侧敲击。图6(b)中齿轮敲击时间历程开始时等于-1，说明了两齿轮处于分离状态，之后突然出现大于1的情况，说明两齿轮在AB侧发生了敲击。随着两齿轮在啮合处的变形以及轻微敲击，敲击时间历程也出现了大于1的情况，最后两齿轮逐渐分离，敲击时间历程重新等于-1。对比图6(c)和图5(c)变速器箱体测点1处的振动频谱图可知，由于空套齿轮发生了单侧敲击，敲击激起了箱体更多频率成分，图6(c)频率成分比图5(c)复杂很多，啮合频率附近的传动轴调制频率更加密集，负载齿轮对z1z2第5阶啮合频率幅值(0.108m/s2)比空套齿轮正常啮合常态下(0.08m/s2)也增大了。

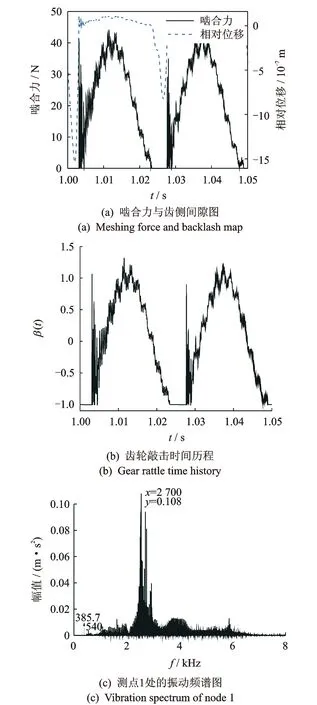
图6 转速波动25 r/min时的敲击情况图Fig.6 Rattle case of the speed fluctuation is equal to 25 r/min

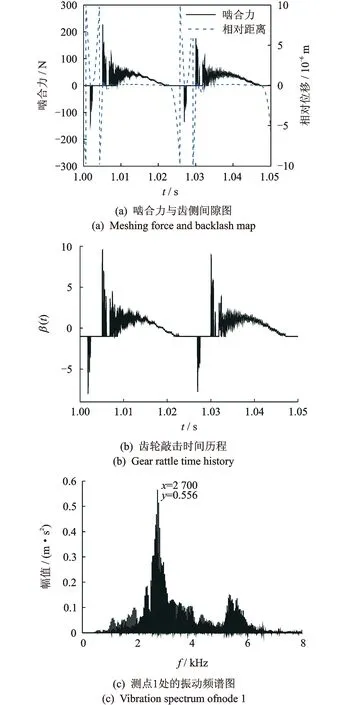
图7 转速波动30 r/min时的敲击情况图Fig.7 Rattle case of the speed fluctuation is equal to 30 r/min

当转速波动为30 r/min时，从图7(a)中可看出，齿轮z5与z6在AB侧与CD侧(见图3)都发生了敲击,即发生了双侧敲击(齿轮相对位移由0.01 mm向-0 mm变化之后又由-0.01 mm向+0 mm变化)。开始时齿轮z6由C侧向z5的D侧运动，齿轮之间没有接触，啮合力为0。当齿轮相对位移大于0，则两齿轮在CD侧发生敲击，齿轮之间随即出现了很大的负啮合力。之后两齿轮分离，齿轮z6经过间隙中间位置并由A侧向z5的B侧运动。此后情况与上面分析的单侧敲击情况相似，只是此时敲击的能量更加大，并且在AB侧首次敲击后由于齿轮变形大而发生了多次震荡敲击，最后两齿轮分离进入下一个敲击周期。图7(b)中的齿轮敲击时间历程出现了两个明显小于-1和大于1的峰值，说明了空套齿轮对z5z6发生了双侧敲击，并且在AB侧敲击时由于还伴随着多次震荡敲击，敲击时间历程在很长时间内都保持大于1。对比图7(c)和图6(c)变速器箱体测点1处的振动频谱图可知，由于空套齿轮发生了双侧敲击，敲击能量比单侧敲击更大。图7(c)中响应幅值比单侧敲击时更大，图中只标出了负载齿轮对z1z2第5阶啮合频率和幅值，其他阶啮合频率几乎被这阶啮合频率的边频带掩盖了，双侧敲击下负载齿轮对z1z2第5阶啮合频率幅值(0.556 m/s2)比单侧敲击下(0.108 m/s2)增大了4倍多。

(11)

图8 各影响因素与敲击强度关系Fig.8 Relations between each factor and percussion strength

4 结 论

1) 运用刚柔耦合方法，综合考虑试验变速器各零部件连接关系、齿轮时变刚度、啮合阻尼、齿侧间隙、发动机转速波动和负载激励、轴承刚度阻尼随运行状态变化特性以及箱体的柔性化特性等因素，建立了可以预测变速器振动噪声特性的刚柔耦合多体动力学模型。

2) 分析了空套齿轮对产生敲击现象的条件以及给出敲击时间历程与各影响因素理论表达式，系统研究了空套齿轮对从正常啮合到单侧敲击和双侧敲击的转变过程以及敲击的各影响因素与敲击强度的关系。研究结果表明，敲击强度除了随空套齿轮与传动轴之间的阻尼系数增大而减小外，几乎都与输入转速波动、齿比z6/z5、空套齿轮转动惯量及输入转速成正比例关系直线上升，但是负载扭矩的变化对空套齿轮敲击影响不大。因此，可以通过合理设计使空套齿轮对保持良好的啮合状态，避免敲击发生。

[1] 韩国胜, 杨为, 李武靖. 微车变速器的轴承-齿轮轴系非线性三维接触动态特性研究[J]. 振动与冲击, 2008, 26(11): 9-12.

Han Guosheng, Yang Wei, Li Wujing. Investigation on 3-d contact nonlinear dynamic characteristic in mini-car gearbox of bearing-gear system[J]. Journal of Vibration and Shock, 2008, 26(11): 9-12.(in Chinese)

[2] Rocca E, Russo R. Theoretical and experimental investigation into the influence of the periodic backlash fluctuations on the gear rattle[J]. Journal of Sound and Vibration, 2011, 330(20): 4738-4752.

[3] Brancati R, Rocca E, Russo R. An analysis of the automotive driveline dynamic behaviour focusing on the influence of the oil squeeze effect on the idle rattle phenomenon[J]. Journal of Sound and Vibration, 2007, 303(3): 858-872.

[4] 陈小安, 缪莹赞, 杨为, 等. 基于有限单元法的多间隙耦合齿轮传动系统非线性动态特性分析[J]. 振动与冲击, 2010, 29(2): 46-49.

Chen Xiaoan, Miao Yingyun,Yang Wei, et al. Nonlinear dynam ic characteristics analysis of a gear transmission system with multiple clearances based on finite element method[J]. Journal of Vibration and Shock, 2010, 29(2): 46-49. (in Chinese)

[5] 符升平, 项昌乐, 姚寿文, 等. 基于刚柔耦合动力学的齿轮传动系统动态特性[J]. 吉林大学学报: 工学版, 2011, 41(2): 382-386.

Fu Shengping, Xiang Changle,Yao Shouwen, et al. Dynamic characteristic of gear transmission system based on rigid and flexible coupled dynamics[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(2): 382-386. (in Chinese)

[6] Fietkau P, Bertsche B. Influence of tribological and geometrical parameters on lubrication conditions and noise of gear transmissions[J]. Mechanism and Machine Theory, 2013, 69: 303-320.

[7] 郭荣, 裘剡, 章桐, 等. 手动变速箱空挡齿轮敲击问题的影响因素分析[J]. 江苏大学学报: 自然科学版, 2013, 34(4): 378-383.

Guo Rong, Qiu Shan, Zhang Tong, et al. Multifactor analysis of neutral gear rattle in automobile manual transmission[J]. Journal of Jiangsu University: Natural Science Edition, 2013, 34(4): 378-383. (in Chinese)

[8] Barthod M, Hayne B, Tébec J L, et al. Experimental study of gear rattle excited by a multi-harmonic excitation[J]. Applied Acoustics, 2007, 68(9): 1003-1025.

[9] 郭磊, 郝志勇, 蔡军, 等. 汽车变速箱齿轮传动系动力学振动特性的研究[J]. 振动与冲击, 2010 (1): 103-107.

Guo Lei, Hao Zhiyong, Cai Jun, et al. Vibration characteristics of transmission gear-train for a car[J]. Journal of Vibration and Shock, 2010 (1): 103-107. (in Chinese)

[10]Craig R R. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7): 1313-1319.

[11]李润方，王建军. 齿轮系统动力学-振动、冲击、噪声[M]. 北京：科学出版社，1997：345-349.

[12]Maatar M, Velex P. An analytical expression for the time-varying contact length in perfect cylindrical gears: some possible applications in gear dynamics[J]. Journal of Mechanical Design, 1996, 118(4): 586-589.

[13]胡鹏, 张义民, 王倩倩. 含侧隙及时变刚度的多级齿轮非线性响应分析[J]. 振动、测试与诊断, 2013, 33(S1):115-119.

Hu Peng,Zhang Yimin,Wang Qianqian. Nonlinear dynamic analysis of spur gear pairs with gear backlash and time-varying stiffness[J]. Journal of Vibration, Measurement & Diagnosis. 2013, 33(S1):115-119. (in Chinese)

[14]Kasuba R, Evans J W. An extended model for determining dynamic loads in spur gearing[J]. Journal of Mechanical Design, 1981, 103(2): 398-409.

[15]吴昊. 滚动轴承动特性及轴承—转子系统动力学模型研究[D]. 上海：华东理工大学, 2011.

10.16450/j.cnki.issn.1004-6801.2016.06.015

*汽车零部件先进制造技术教育部重点实验室2010年度开放基金资助项目(2010KLMT04)

2014-12-09；

2015-04-17

TH132.46； U463.212

丁康，男，1957年8月生，博士、教授。主要研究方向为车辆性能检测与故障诊断技术。曾发表《齿轮及齿轮箱故障诊断实用技术》(北京：机械工业出版社，2005年)等论著。 E-mail: kding@scut.edu.cn