电力变压器缩尺模型振动试验及其声学模型*

黄国兴， 阮学云,2， 李志远， 魏浩征

(1.合肥工业大学噪声与振动工程研究所 合肥，230009)(2.安徽理工大学机械学院 淮南，232001)



电力变压器缩尺模型振动试验及其声学模型*

黄国兴1， 阮学云1,2， 李志远1， 魏浩征1

(1.合肥工业大学噪声与振动工程研究所 合肥，230009)(2.安徽理工大学机械学院 淮南，232001)

首先，根据某电力变压器的缩尺比例模型在不同激振频率下箱壁振动相位和振幅的测试结果，得出当激振频率超过7阶模态频率时，其相位和振幅呈随机分布的结论，确定了电力变压器简化为点声源的划分形式；其次，建立了户外半开空间内电力变压器相干虚源模型，该模型考虑了声线多次反射形成的无限个虚源之间的干涉效应；最后，应用该相干虚源模型对存在相位关系的电力变压器组辐射声场进行计算，通过与边界元模型、ISO9613模型计算结果与实测值进行对比。结果表明，该相干虚源预测模型因考虑了相位信息，能反映出声波在不同位置处的传播趋势，比原有的ISO9613模型更为准确，验证了所提理论模型的可行性。

电力变压器； 振动试验； 缩尺比例模型； 噪声预测； 相干虚源法； 半开空间

引 言

变压器是连续工作的，它产生的噪声是人耳较为敏感的低频噪声。随着城市用电需求的不断增加，电力变压器运行造成的环境影响与人民群众逐步增长的环保意识间的矛盾日益突出[1]。目前，变压器的研究主要包括变压器振动和噪声的产生机理、声学特性、降噪措施以及相关的环保标准等[2]，但是对变压器户外噪声的研究却不多。变压器户外辐射噪声水平是进行变电站设计和改造的重要参数，因此对其研究具有重要意义。文献[3]将变压器简化为一个点声源并对其噪声辐射进行了计算。文献[4]根据变压器箱壁表面法向加速度数据利用Helmholtz积分公式来预测变压器声场声压。文献[5]指出当考虑地面变电站内其他变压器、围墙、本体尺寸及其他建筑对变压器声辐射的影响时，仍使用点声源模型将会产生较大的误差。此外，若获取足够多的变压器箱壁表面法向加速度数据进行计算，可以较好的预测变压器噪声，但该方法计算量大，且现场变压器表面振动数据获取往往不太容易，因此该方法工程应用性不强。

为解决上述问题，笔者在建立电力变压器户外声传播模型时，将其简化为多个点声源。马宏彬等[6]对500 kV单相电力变压器进行了振动与噪声的同步检测，发现噪声频谱与振动频谱主要集中在100～500 Hz的频率范围内，幅值有明显的对应，并由此确定了电力变压器振动与噪声之间的关联性。程锦等[7]利用振动法在线检测变压器绕组及铁心状况时也得到类似结论。因此对某电力变压器进行缩尺比例模型振动试验，通过测量表面测点振动相位和振幅来对应研究该点噪声的幅值和相位是可行的。由于户外电力变压器大多处于两个防火墙和地面组成的半开空间内，声线在传播时存在大量反射且不同反射波存在干涉现象，笔者提出了电力变压器相干虚源模型，该模型考虑了各面反射声波间的干涉现象，同时该模型还可根据不同的边界阻抗率进行计算，应用范围广。

1 电力变压器噪声辐射机理与噪声频谱分析

电力变压器的噪声主要由两部分组成:电力变压器本体噪声和冷却系统产生的连续性噪声。电力变压器本体噪声主要由铁心振动噪声磁致伸缩引起[8-9]。因铁心磁致伸缩的非线性，以及沿铁心内框和外框的磁通路径长短不同等原因,故铁心振动与绕组振动有所不同，其噪声频谱中除了基频外,还包含有高次谐频噪声[10-11]。

图1为某220 kV变电站电力变压器实测的噪声频谱图。从该图可以看出，电力变压器的噪声主要集中在100，200和300 Hz频段处，其中100 Hz的噪声为主要噪声成分，整个频谱以中低频为主。因低频噪声波长较长，有很强的绕射和透射能力，在空气中随距离衰减较慢，噪声传递距离远，影响范围广[12]。

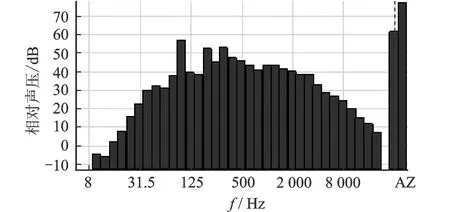
图1 220 kV电力变压器噪声频谱图Fig.1 Noise spectrum of 220 kV power transformer

2 电力变压器箱壁缩尺模型表面相位试验

对于受声点距实际声源较远的情况，可以简化为一个点声源，而对于像电力变压器尺寸较大的声源，且又受防火墙的反射和衍射影响，就不能简单地简化为一个点声源，因此得到各点声源的振幅和相位尤为重要。以往噪声预测时，其简化声源的声压振幅一般采取等效源法，相位在能量法中则不予考虑。笔者研究的是声线经多次反射后形成的相干声场，点声源相位大小对声场预测结果影响较大，为准确得到点声源的相位信息，则需要得到电力变压器箱壁的实际相位分布信息。考虑到安全和测试条件受限制等原因，对现场变压器布置大量的测点并进行振动噪声测试十分困难，因此笔者基于相似理论，设计某电力变压器本体箱壁的缩尺模型，通过测试变压器箱壁模型表面测点的振型来研究对应的噪声幅值和相位。

2.1 缩尺比例模型的理论基础

缩尺模型的理论基础来源于缩尺模型的相似性原理,包括几何相似性原理和物理相似性原理，具体为模型与真型的尺寸关系、波长关系、频率关系及声场关系。当缩尺模型与真型几何相似比为1∶n时，即有以下关系[13]

(1)

其中：Lm，fm，λm分别为缩尺模型的尺寸、频率和波长；L，f，λ分别为实际真型的尺寸、频率和波长。

2.2 缩尺模型几何尺寸与试验

本缩尺模型为变压器主要辐射面中最大面积的一个箱壁的1∶10缩尺模型，该模型只有竖向瓦楞结构，即只有竖向加强筋。箱壁模型几何尺寸为840 mm×450 mm×0.5 mm(长×宽×厚)，材料为Q235，共有8个加强筋均布在箱壁表面,四周金属压板有通孔，用于连接固定在一较大质量刚性试验箱体上，形成固支架结构。其几何示意图见图2。

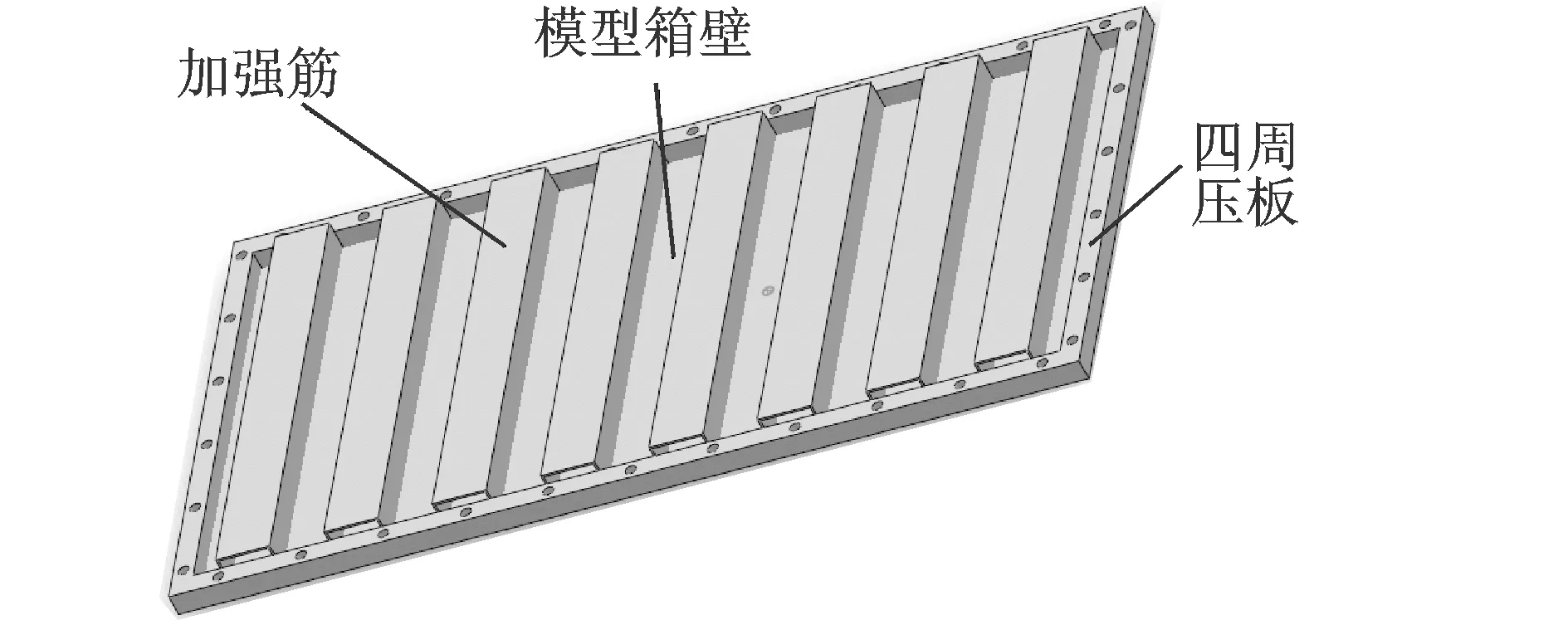
图2 变压器箱壁的缩尺模型几何示意图Fig.2 Scale model of transformer tank wall geometry diagram

电力变压器主要优势频率在100～500 Hz之间，根据缩尺比例n=10，这里考察正弦激励信号频率为1 000～5 000 Hz下表面各测点的振动幅值和相位分布情况。激振频率由低到高分别选择100，200，400，600，800，1000，2 000，3 000，4 000和5 000 Hz共10个频率。在试验测试过程中，激振器位于缩尺模型下侧面的下方，模型受其激励进行振动。为了客观地反映箱壁表面振动相位、振幅的分布，测点按每隔0.05 m进行划分，共计120个测点。因声音在金属中传播速度较快，达到5 200 m/s，即使对考察频率为5 000 Hz的纯音，其波长也有1.04 m，而本次试验的测点间隔为0.05 m,仅为其波长的1/20，精度足够满足要求。另外，本次试验得到的振幅和相位均为相对值，因此选择了模型中部位置的一固定参考点。相位测点与测试参考点分布见图3，实际试验时的测试系统示意图如图4所示。

图3 电力变压器箱壁模型表面测点分布(单位：mm)Fig.3 The measuring point distribution of model surface about power transformer (unit：mm)

图4 电力变压器缩尺模型测试系统示意图Fig.4 Scale model test system schematic diagram of power transformer

2.3 测试结果与分析

本次试验在对各测点的振型测试之前，对缩尺模型进行了模态试验，得到了该模型的各阶频率和相应的振型图。前10阶模态频率见表1。

表1 电力变压器箱壁缩尺模型前10阶模态频率

Tab.1 The first 10 order modal frequency of power transformer surface scale model

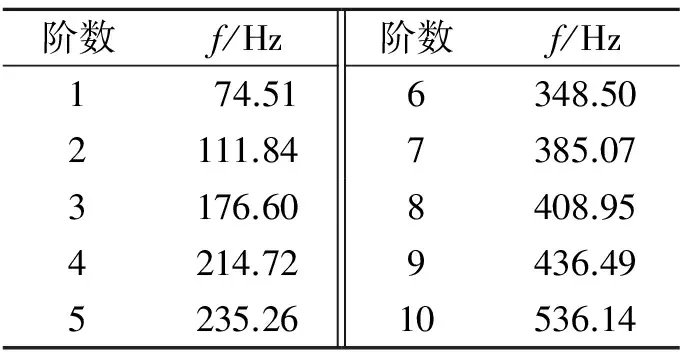
阶数f/Hz阶数f/Hz1 74．516348．502111．847385．073176．608408．954214．729436．495235．2610536．14

由表1可知，前10阶频率从74.51 Hz变化到536.14 Hz，根据缩尺比例模型原理，实际变压器的前10阶频率在7.45～53.61 Hz之间，小于其噪声的主要优势频率100～500 Hz。

模型表面振型测试时激振频率较多，根据测试结果，这里选择100,200,400和1 000 Hz激振频率下的数值，并绘制了模型表面三维相位网格分布图，如图5～图8所示。

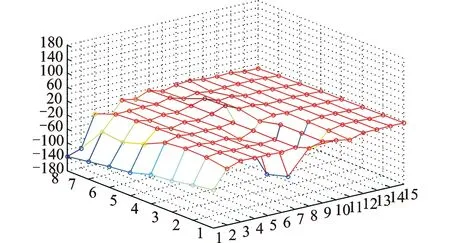
图5 模型表面测点相位三维网格分布(100 Hz)Fig.5 Three-dimensional grid distribution about phase of measuring points on the surface of model (100 Hz)

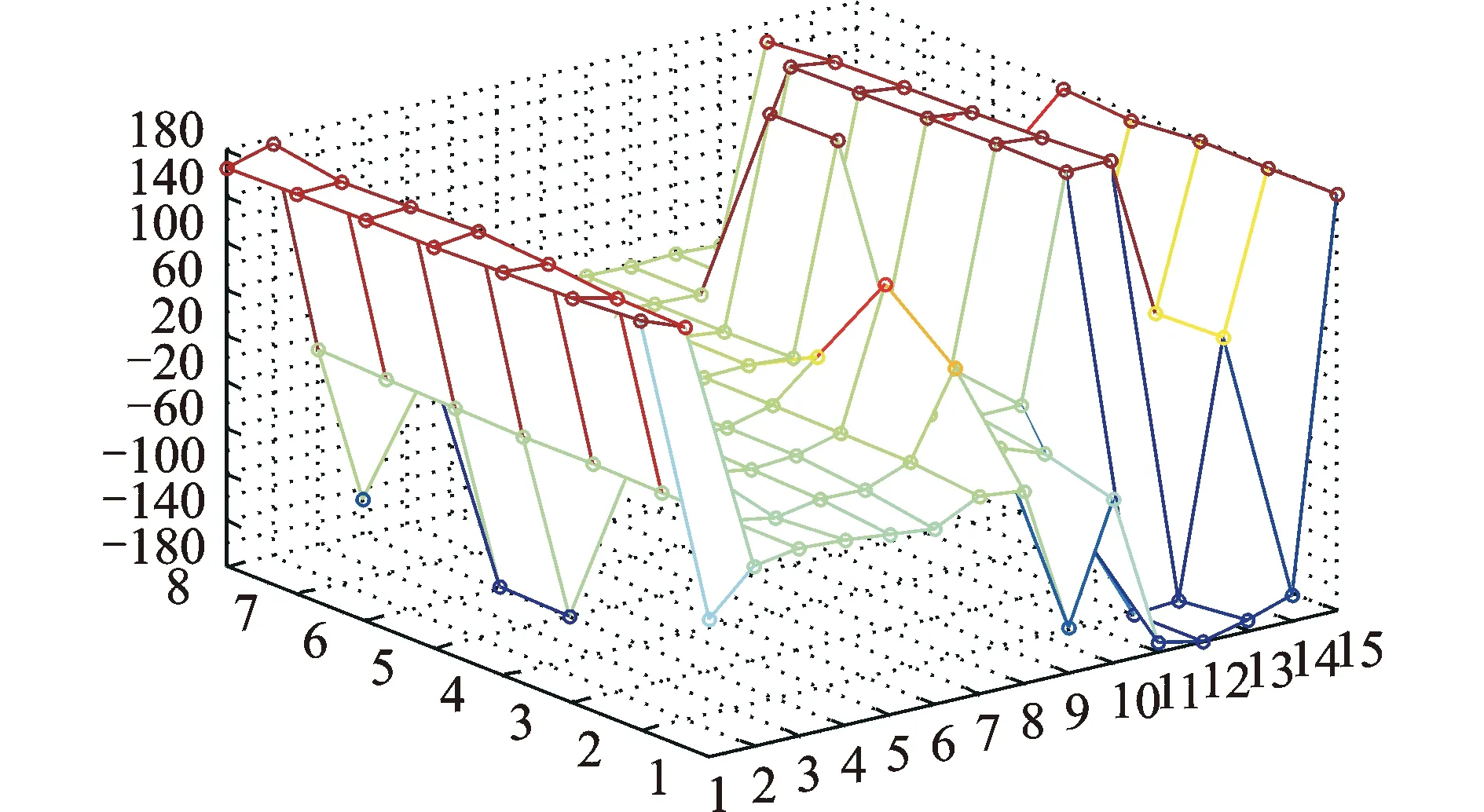
图6 模型表面测点相位三维网格分布(200 Hz)Fig.6 Three-dimensional grid distribution about phase of measuring points on the surface of model (200 Hz)

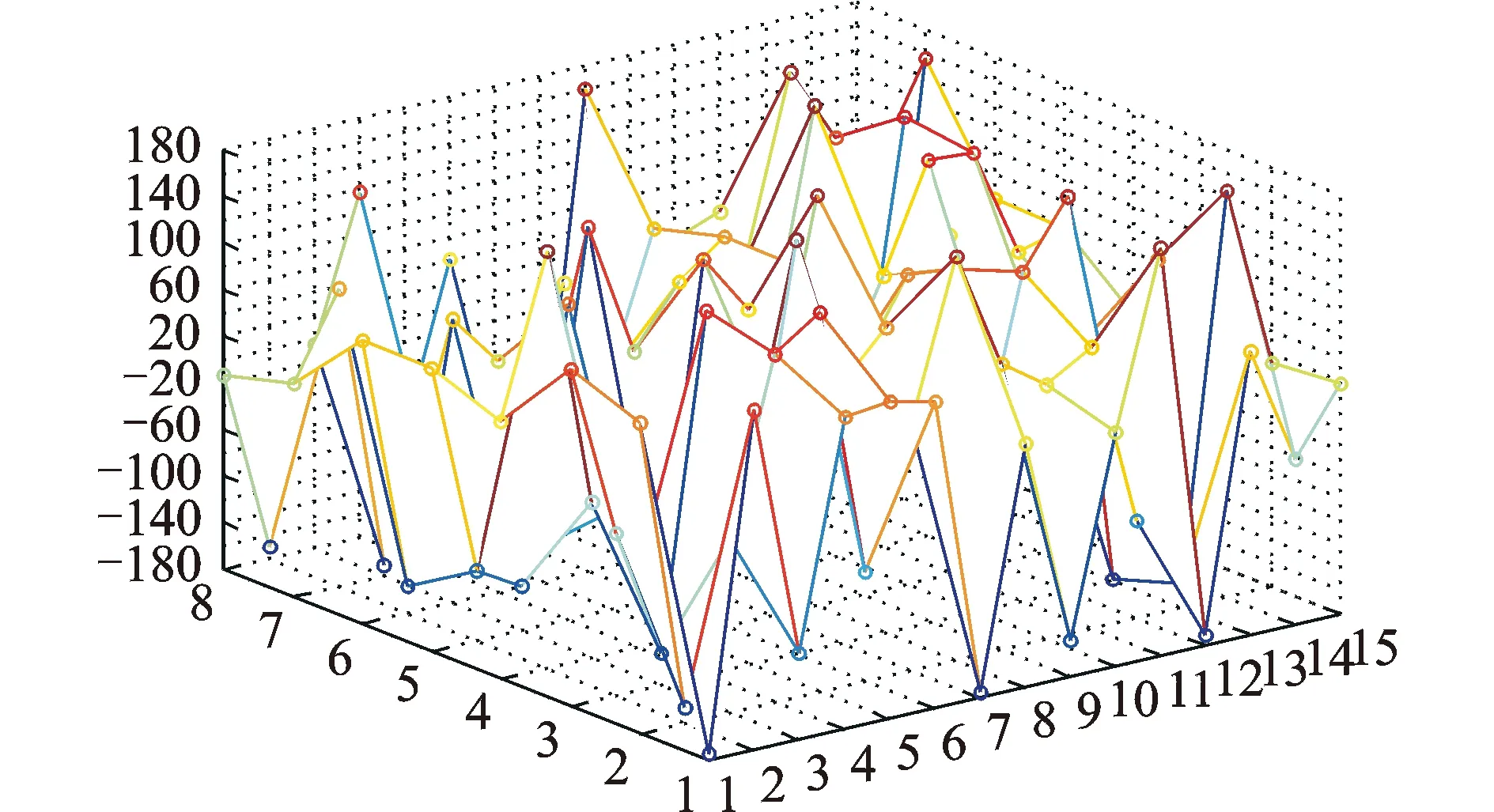
图7 模型表面测点相位三维网格分布(400 Hz)Fig.7 Three-dimensional grid distribution about phase of measuring points on the surface of model (400 Hz)

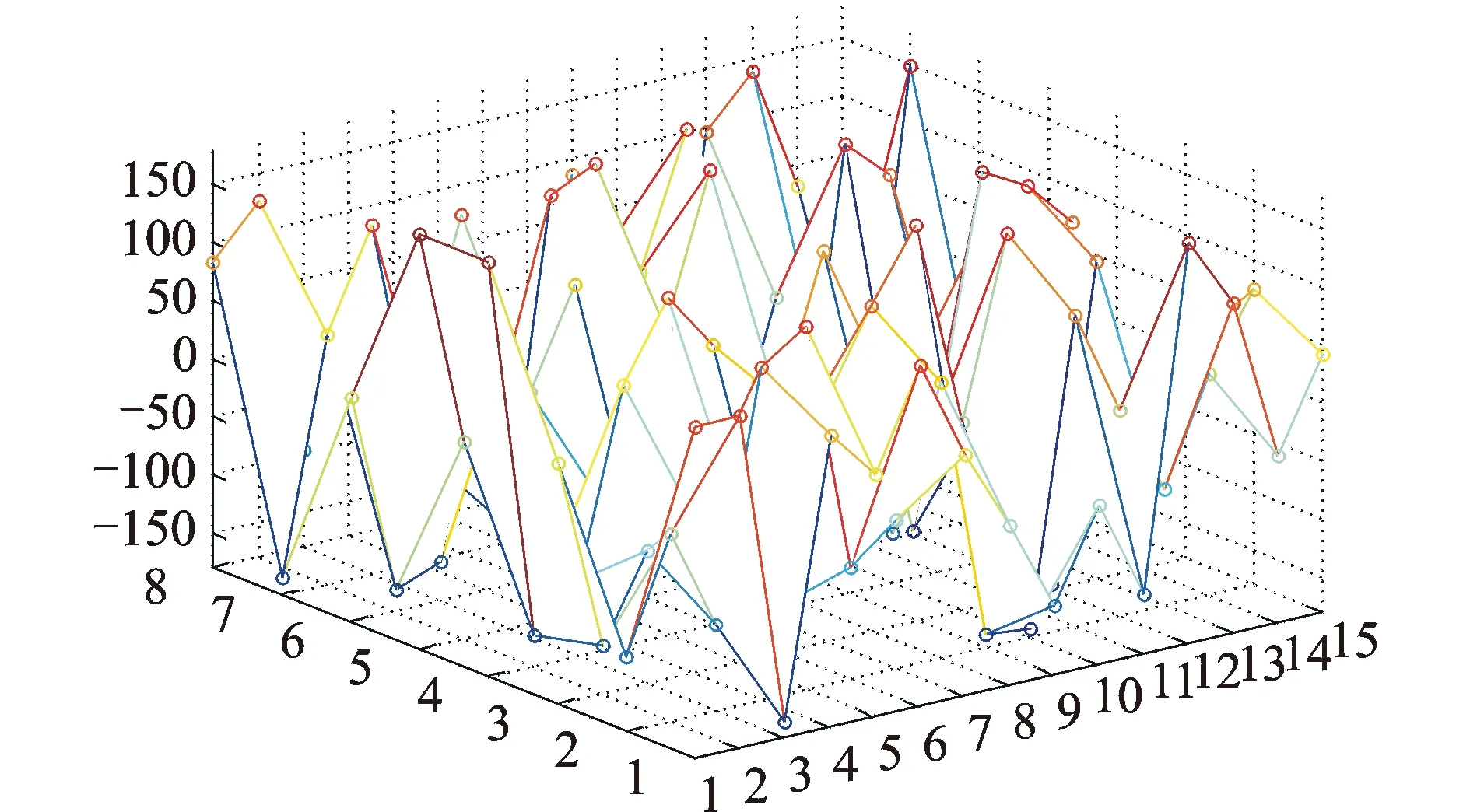
图8 模型表面测点相位三维网格分布(1kHz)Fig.8 Three-dimensional grid distribution about phase of measuring points on the surface of model (1kHz)

由图5～图8可知，在f=100 Hz时，接近其1阶频率的情况下，测点相位主要集中在-20°～20°，其测点个数占所有测点的75%，相位比较集中；当f=200 Hz时，相位主要集中在-20°～20°，其测点个数占所有测点的51%；当f=400 Hz时，相位分布开始呈随机变化，相位在-20°～20°测点个数占所有测点的15%；当f=1 kHz时，相位分布更为分散，在-20°～20°的测点个数占所有测点的10%，这个比例几乎和此区域的相位范围占总相位360°的比例(40/360)相当。因此随着频率的提高，电力变压器缩尺模型的箱壁的相位分布范围更广，呈随机分布状态，即认为各测点相位落在-180°～180°之间的概率都是等同的。

同样的，对各测点的振幅也进行了相同的比较，得到和相位基本一致的结论。在激振频率达到400Hz时随机特性表现也开始明显，考虑是因为电力变压器箱壁模型表面布置有多个加强筋，不同的测点位置对测试结果影响很大，这与变压器表面自身结构复杂有关。在对电力变压器现场振动监测，也得到类似的结论[11]。

通过对电力变压器箱壁缩尺模型表面相位和振幅进行测试，并根据缩尺比例模型理论进行分析可知，电力变压器的表面振动由于自身结构特点，表面振型复杂。振动频率越高时，筋板结构高频特性逐渐体现，会出现许多的局部模态。本研究对象结构简单，为大面积钣金结构，且由于考虑的优势频率上限低，高频局部模态不在其范围内，故对此不予考虑。实际上，在笔者考虑的优势频率范围内，缩尺模型表面振动的随机特性随着振动频率的提高表现越为明显。当实际真型变压器的振动频率为40 Hz，即超过其7阶频率(38.51 Hz)时，各离散测点的幅值和相位的随机特性表现明显。根据变压器噪声优势频率为100～500 Hz可知，电力变压器表面噪声相位和振幅在以上频率范围内均呈随机分布。根据声场干涉理论，具有无规相位的声波叠加时，认为不发生干涉，即按照能量法进行叠加[14]。因此，对于单个的单向变压器，可按划分的等效点声源法进行，各点声源对受声点的声场影响按照能量法进行叠加，即不考虑相位的影响。

3 考虑相位的电力变压器噪声

由缩尺比例模型的振动试验得到电力变压器表面划分的各等效点声源按照能量法叠加，但针对某个具体简化的点声源，考虑到户外电力变压器大多处于两个防火墙之间，各点声源在辐射时产生大量的多重反射声构成相干声源，其周围声场为相干声场，而户外噪声预测算法不考虑相位，无法进行相干声场计算。针对以上情况，笔者提出了考虑相位的电力变压器相干虚源模型，主要用于计算半开空间内声源激发的外部相干声场。如图9所示，侧面1和侧面2代表两侧防火墙。W为两个侧面之间距离，H为侧面1和侧面2的高度。R，E1R和E2R分别表示受声点和左右两个侧面上方绕射点。侧面1、侧面2及地面的归一化导纳为βi(i=1,2,3)。

图9 虚源构造示意图Fig.9 Structure diagram of image source

根据虚声源产生原理，当受声点在半开空间外部右侧时，左侧虚声源(m≤0)起作用，此时声线在两个屏障之间多次反射后，经过E2R衍射到达受声点R。反之，当受声点在半开空间外部左侧时，声线最后经过E1R衍射到达受声点R。另外，本研究半开空间地面为无限大刚性平面，因此在EiR(i=1,2)点的绕射声经地面反射后到达受声点R，这里给出了虚受声点R′。

半开空间的整个声场是由声源和所有虚源共同决定的，虚源是由声源在各反射面不停反射生成的，无穷多次的反射产生了无穷多个虚源。于是，总声场可看成是由所有虚源的影响综合决定的，可得受声点的总声压为

(2)

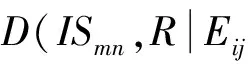
对于反射面的单次反射系数Qi，Lemire认为可以使用一个无限大界面上球面波反射场的近似解来求取[16]，即

(3)

其中：Rpi为第i个反射面上的平面波反射系数。

(4)

其中:θmn为从虚源ISmn到受声点的声波传输路径在该反射面上的正入射角；βi为第i个界面的法向比声纳。

式(3)中F(w)为界面损耗系数[17-19]，可表示为

(5)

其中:erfc为余补误差函数;w为数值距离参数。

w与虚源的阶数m，n入射角θmn以及相应的边界有关，定义为

(6)

笔者提出的半开空间相干虚源模型给出了声源在反射或衍射时的相位信息，因此可以进行矢量叠加，可用于计算户外相干声场。

4 某电力变压器组辐射声场数值仿真

前面给出了点声源在半开空间内激发的声场预测公式，实际计算电力变压器组户外辐射噪声前，须将单个变压器表面划分成若干个单元，每个单元相当于一个点声源，根据其表面单元点声源相位和振幅的随机分布特点，单个电力变压器本身的各点声源按不相干声源进行计算。对于由A相、B相和C相组成的电力变压器组，各相电力变压器总相位相差120°，因此在各个变压器相同位置处的各点声源相位差需设置为120°，此时应按相干声源进行计算。其中等效点声源的源强根据划分点声源的个数，按电力变压器声功率级的能量平均进行计算。电力变压器组布局如图10所示。

图10 电力变压器组布局图Fig.10 Power transformer group layout

4.1 计算模型

以某一电力变压器组作为研究对象，根据笔者提出的相干虚源模型计算其对户外噪声的影响。该模型由3个变压器组成，按照A相、B相和C相间隔分布，反射面由4个平行的防火墙与刚性地面组成。各个变压器尺寸相同，其本体高度为4.6 m，长为4.0 m，宽为8.9 m。防火墙高度为6.8 m，长为15 m，防火墙之间距离为7.5 m。电力变压器中的防火墙与地面均为刚性反射面，相邻变压器总声源相位相差120°。考虑变压器模型区域对称性，计算场点网格区域大小设置为100 m×100 m，网格间距为2 m×2 m，高度设为1.5 m，覆盖模型区域的1/4。为与各方法的模型中单点计算结果对比，在计算场点网格的45°对角方向距电力变压器组中心由近至远设置了25个受声点，每个受声点高度为1.5 m，各受声点横坐标间距为2 m。

根据声源的相位分布特点，将各个变压器分别离散成35个均匀分布的点声源，各个变压器声源的总声功率设为95 dBA，根据电力变压器现场噪声频谱中优势频率为100 Hz，笔者选择点声源的计算频率亦为100 Hz。电力变压器各表面单元划分的点声源分布与几何尺寸见图11。

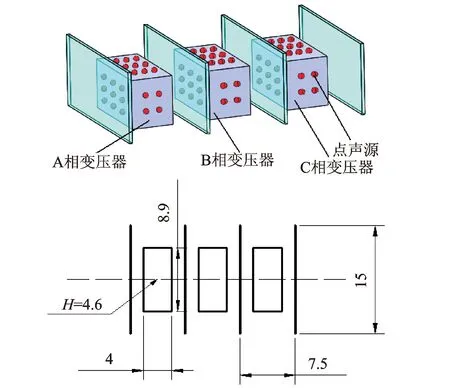
图11 电力变压器组点声源分布与几何尺寸图(单位：m)Fig.11 Noise source distribution and dimensional drawing of power transformer group (unit：m)

4.2 计算结果

分别利用边界元算法、基于ISO9613的Cadna/A预测软件和笔者提出的户外相干虚源计算模型进行噪声网格地图数值仿真。

通过边界元法160 h的计算后，得到电力变压器组100Hz的噪声网格分布图如图12所示。

应用基于ISO9613标准的Cadna/A预测软件对电力变压器组进行噪声地图绘制，结果见图13。

应用笔者提出的相干虚源模型，对电力变压器组进行数值仿真，耗时36.8 min，得到100 Hz下的噪声网格分布图如图14所示。

图12 基于边界元计算的噪声网格分布Fig.12 Noise distribution grid based on boundary element method

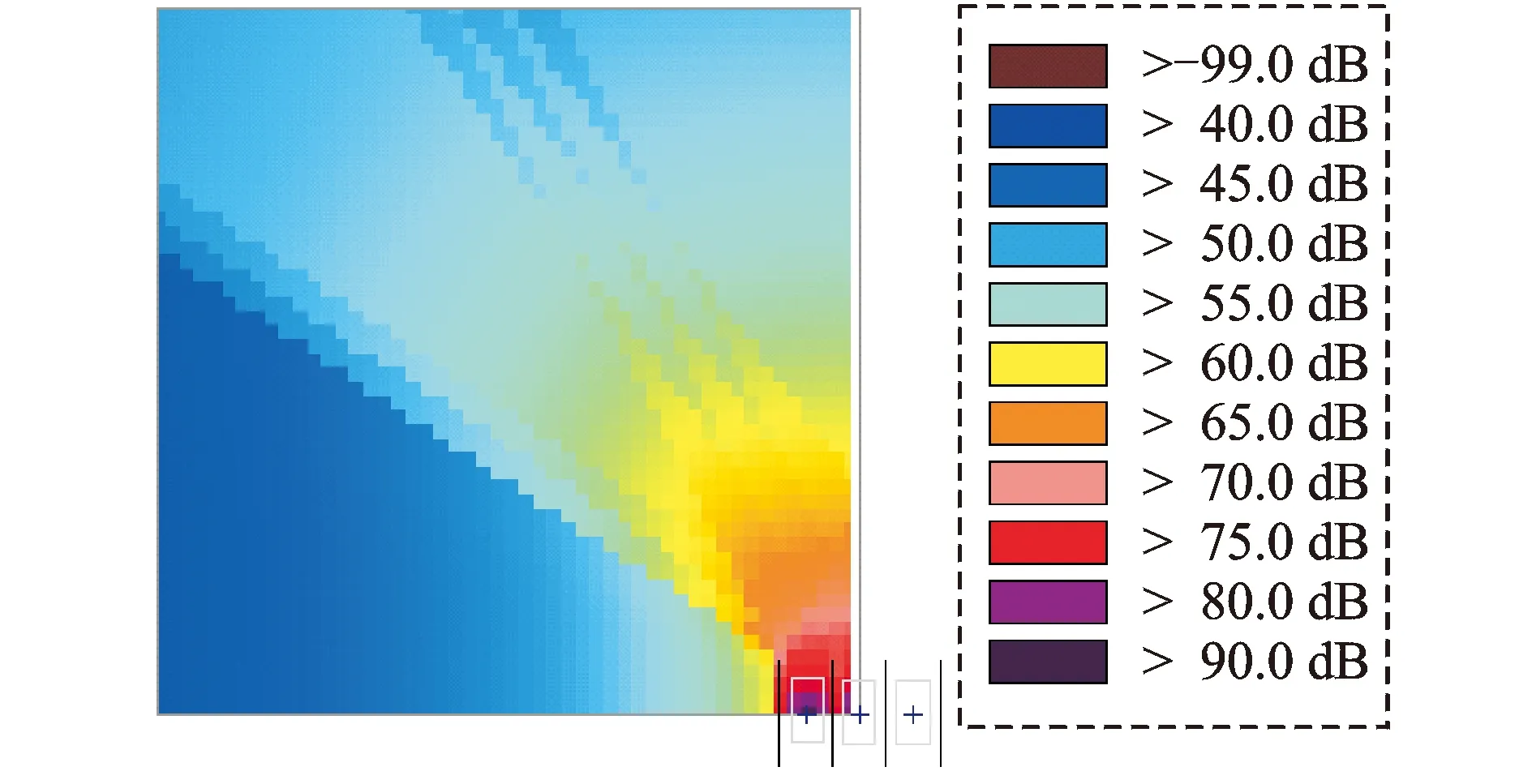
图13 基于ISO9613的噪声网格分布(Cadna/A)Fig.13 Noise distribution grid based on ISO9613 (Cadna/A)

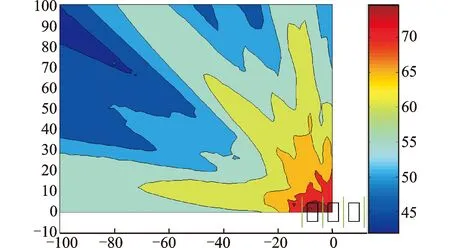
图14 本计算模型的噪声网格分布Fig.14 Noise distribution grid calculation model of the proposed calculation model

利用本相干虚源模型、边界元法及基于ISO9613标准的Cadna/A预测软件对场点网格的对角方向的25个受声点进行计算，并将其计算结果与实测值进行对比，如图15所示。

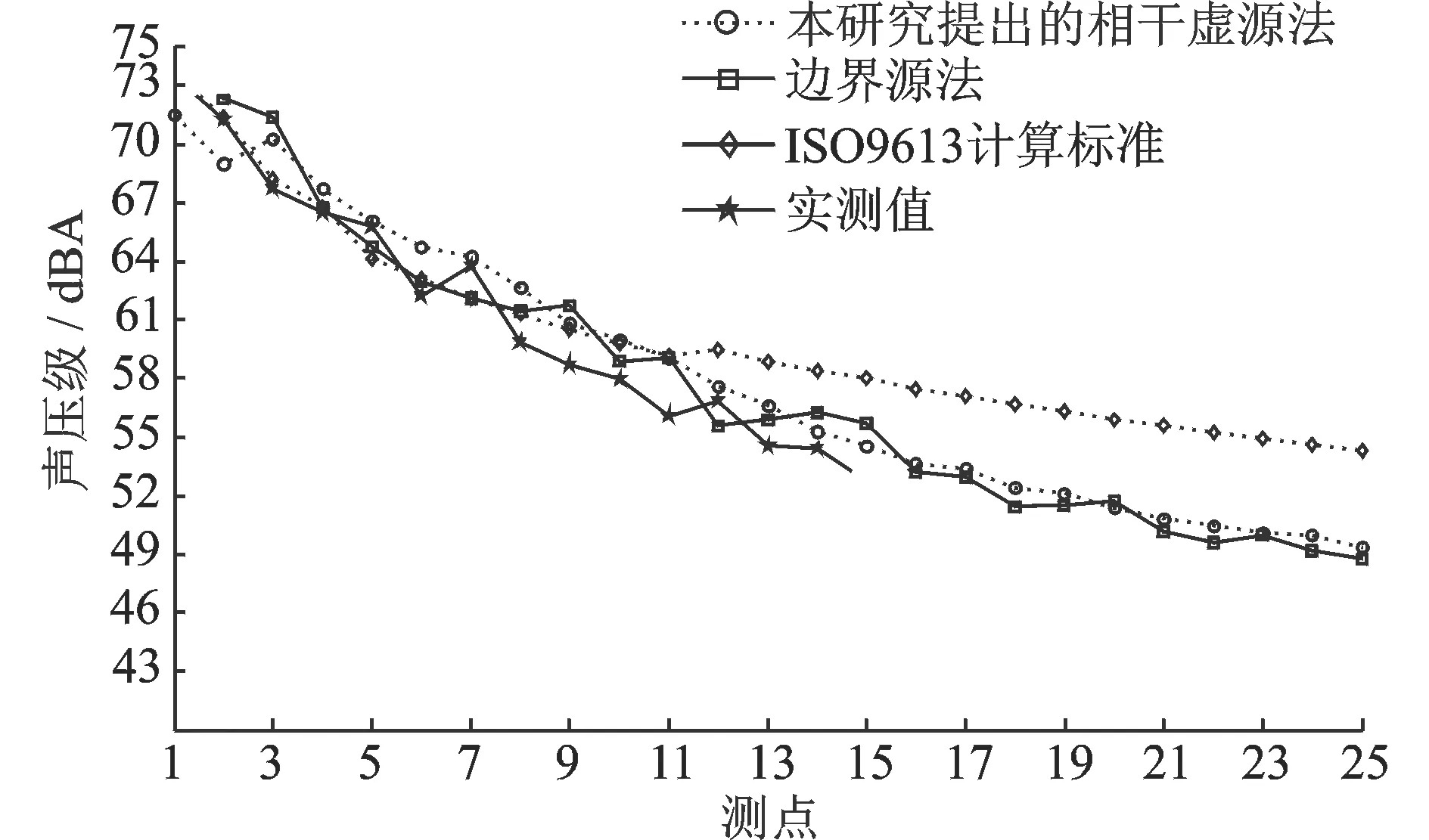
图15 3种方法计算受声点的声压值与实测值的对比Fig.15 The contrast of pressure value of the receiver between three kinds of method and the measured values

由图12～图14可知:边界元法与本算法因为考虑了相位，反映了相干声场的波动性，可以看出有明显的干涉条纹；利用ISO9613标准的Cadna/A预测软件则无明显的干涉条纹，这是因为其算法中没有考虑相位，只是能量的叠加；对比边界元法和本算法绘制的噪声地图，声压级对应的颜色分布趋势相同，吻合度较高，而本算法的计算时间则大大缩短。

由图15可知，IS09613标准计算的声压级值能反映出随着受声点不断远离声源，其声压级不断降低的趋势。当受声点距离声源较近时，IS09613标准计算结果要低于其他方法计算的声压值，这是由于没有考虑相干虚源叠加效果所致；而当受声点距离声源较远时，IS09613标准计算相比其他两种方法结果又偏大，这是因为该算法中的镜像虚源法未考虑多次反射时，声线与边界面入射角度的变化引起反射损失逐渐增大的实际情形，因此造成ISO9613计算值偏高。由图15还可知，本相干虚源模型计算受声点的噪声值与边界元法、实测值相比，误差较小，除了个别点达到3 dB，其他各点误差基本上都在2 dB以内。尤其受声点处于远场时，其声压级误差更小，能反映在不同位置处的传播趋势，比原有的ISO9613模型更接近测试结果，证明了所提理论模型的有效性。

5 结束语

笔者进行了电力变压器的缩尺比例模型试验，在确定其划分为点声源的基础上，通过依次计算点声源在半开空间内产生的每个虚源到达接收点遇到的所有边界的声波反射系数，推导出了电力变压器户外声场传播相干虚源模型。对某实际电力变压器组噪声预测声学模型进行了计算，通过与边界元法建立的模型计算结果和实测值进行对比可以看出，所推导的电力变压器相干虚源模型由于考虑了声波的相位，将球面声波的反射引入不同边界的相干虚源模型，提高了预测精度，比传统的ISO9613模型能更好地预测电力变压器户外声场传播的衰减规律，有助于提高电力变压器的户外噪声预测水平。

[1] 谭闻，张小武．电力变压器噪声研究与控制[J]．高压电器，2009，45(2)：70-76．

Tan Wen，Zhang Xiaowu．Investigation and control of power transformer noise[J]．High Voltage Apparatus，2009，45(2)：70-76．(in Chinese)

[2] IEEE Committee Report.Bibliography on transformer noise[J]. IEEE Transactions on Power Apparatus & Systems,1968,87(2):372-387.

[3] Gordon C G. A method for prediction the audible noise emissions from large outdoors power transformers[J]. IEEE Transactions on Power Apparatus & systems,1979,98(3):1109-1112.

[4] Usry G O, Saha P.Prediction of far field sound radiation from transformers[J]. IEEE Transactions on Power Apparatus & systems,1980,99(1):358-364.

[5] 顾晓安，沈荣瀛，徐基泰.国外变压器噪声研究的动向[J].变压器，2002，399(6)：33-37.

Gu Xiaoan,Shen Rongying,Xu Jitai.Trend of transformer noise research abroad[J].Transformer,2002,399(6):33-37.(in Chinese)

[6] 马宏彬，何金良，陈青恒.500kV单相电力变压器的振动与噪声波形分析[J].高电压技术，2008,34(8):1599-1604.

Ma Hongbin,He Jinliang,Chen Qingheng.Vibration and sound waveform analysis of 500 kV single phase power transformer [J].High Voltage Engineering, 2008,34(8):1599-1604.(in Chinese)

[7] 程锦, 李延沐,汲胜昌，等. 振动法在线监测变压器绕组及铁心状况[J].高电压技术，2005，31(4)：43-45，48.

Cheng Jin,Li Yanmu,Ji Shengchang,et al.Application of vibration method on monitoring the winding and core condition of transformer [J].High Voltage Engineering,2005,31(4):43-45,48.(in Chinese)

[8] 余尤好, 陈宝志. 大型电力变压器的噪声分析与控制[J].变压器，2007,44(6)：23-26，44.

Yu Youhao,Chen Baozhi.Noise analysis and control of large power transformer[J].Transformer,2007,44(6)：23-26,44.(in Chinese)

[9] 虞兴邦，姜在秀，韩涛.变压器的噪声及其降低[J].噪声与振动控制，2001(5)：35-38.

Yu Xingbang,Jiang Zaixiu,Han Tao. Noise of transformer and its reduction[J].Noise and Vibration Control ,2001(5)：35-38.(in Chinese)

[10]柳泽荣. 变压器安装与运行[J].变压器 ,2008,45(6): 48-52.

Liu Zerong. Installation and operation of transformer [J].Transformer,2008,45(6):48-52.(in Chinese)

[11] 顾晓安，沈密群，朱振江，等. 变压器铁心振动和噪声特性的试验研究[ J ]. 变压器, 2003,40(4):1-4.

Gu Xiaoan,Shen Miqun,Zhu Zhenjiang,et al.Test research on vibrations and noise level in transformer core[J].Transformer,2003,40 (4):1-4.(in Chinese)

[12]李文毅，孙竹森，肖安全，等.三沪直流工程换流站噪声治理[J].中国电力，2008，41(1)：32-35.

Li Wenyi,Sun Zhusen,Xiao Anquan,et al.Noise treatment in three gorges-Shanghai±500kV DC transmission converter stations[J].Electric Power,2008,41(1):32-35.(in Chinese)

[13]吴硕贤，张三明，葛坚.建筑声学设计原理[M].北京:中国建筑工业出版社，2000：192-194.

[14]杜功焕，朱哲民，龚秀芬.声学基础[M].南京:南京大学出版社,2001：230-233.

[15]闵鹤群.开放式办公室内的声场预测方法研究[D].南京：南京大学，2010.

[16]Attenborough K.,Hayek S I,Lawther J M.Propagation of sound above a porous half space[J].Journal of the Acoustical Society of America,1980,68(5),1493-1501.

[17]Kuttruff H.Room acoustics[M]. 2nd. London:Applied Science Publishers Limited,1991：67-83.

[18]Briquet M, Filippi P. Diffraction of a spherical wave by an absorbing plane[J]. Journal of the Acoustical Society of America, 1977,61(2):640-646.

[19]Embleton T F W.Tutorial on sound propagation outdoors[J]. Journal of the Acoustical Society of America, 1996,100(4): 31-48.

10.16450/j.cnki.issn.1004-6801.2016.06.013

*国家“十一五”科技支撑计划资助项目(2006BAA02A21)

2014-10-09；

2014-12-31

TH113.1； TB532； TM721.2

黄国兴,男，1980年8月生，博士、讲师。主要研究方向为机电产品低噪声设计、振动测试与分析等。曾发表《Research on the whole condition loaded noise measurement circuit of power capacitor》(《Applied Mechanics and Materials》2014，Vol.490-491)等论文。 E-mail：guoxinghfut@163.com 通信作者简介：阮学云，男，1978年10月生。博士、副教授。主要研究方向为机械系统动力学。 E-mail：ruanxueyun@163.com