尾门系统约束力对解锁条件的影响研究

李超帅 林森 于波 李瑞生

（华晨汽车工程研究院，沈阳 110000）

尾门系统约束力对解锁条件的影响研究

李超帅 林森 于波 李瑞生

（华晨汽车工程研究院，沈阳 110000）

为解决新车型开发过程中因闭合件系统条件改变导致的锁机构失效问题，对尾门系统建立了数学模型，通过公式推导，将尾门密封条、气弹簧以及缓冲块等系统影响因素统一转换为尾门系统约束力，结合尾门锁内部机构的工作原理，分析了尾门系统约束力对解锁条件的影响，提出了一种精细化的尾门系统约束力与解锁条件的匹配计算方法。同时，提出了计算过程中需要充分考虑的外界影响因素，对计算参数进行了修正，以满足各种工况下尾门锁的功能稳定性。

1 前言

目前，在国内新车型的开发中，锁机构通常借用量产车型中已经成熟应用的产品，往往忽略了不同车型闭合件系统的条件改变对锁机构的影响，难以设计出最优方案，甚至会出现锁机构失效问题。所以，从基本原理上探寻锁机构与闭合件系统条件的匹配方法，解决系统因素导致的锁机构解锁失效问题是很有必要的。本文以两厢车尾门锁与尾门系统的匹配为例进行了解锁可靠性的匹配计算方法分析。

2 尾门系统约束力模型

在不同车型中，尾门的质量、其密封条的布置、气弹簧的力和缓冲块的布置都不相同，这些系统因素的差异形成了不同车型尾门锁机构工作环境的差异，因此，新开发车型中尾门锁机构的匹配应用就需要综合考虑整个尾门系统条件的影响[1～2]。

如图1所示，尾门在关闭状态下处于以尾门铰链为旋转轴，尾门锁、缓冲块、气弹簧以及密封条等尾门附件约束下的平衡状态。其中尾门自身重力以及尾门锁与锁扣之间的拉力提供了尾门在图1所示视图下顺时针方向的旋转力矩，尾门缓冲块、气弹簧以及密封条提供了尾门在图1所示视图下逆时针方向的旋转力矩。在两个方向旋转力矩的约束下，尾门处于平衡状态，即：

式中，M1为尾门自身的重力力矩；M2为尾门锁与锁扣之间的约束力矩；M3为尾门缓冲块提供的支撑力矩；M4为尾门限位块提供的支撑力矩（限位块在设计状态无压缩量，通常预留1 mm间隙进行容差，仅在极限公差情况下M4＞0）；M5为尾门气弹簧提供的支撑力矩；M6为尾门密封条提供的支撑力矩。

图1 尾门关闭状态下力矩平衡示意

在不同车型中，M1及各支撑力矩的大小均不相同，因此，同一尾门锁应用在不同的尾门系统中，其与锁扣之间的约束力矩M2也不相同。尾门锁与尾门锁扣之间的约束力可表示为：

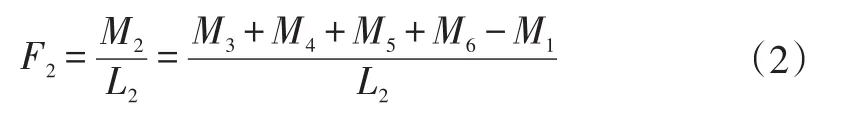
式中，L2为F2以铰链为旋转轴线的力臂。

式（2）将尾门密封条、缓冲块以及气弹簧等所有条件的作用效果集中体现在系统约束力F2上，它是影响尾门解锁可靠性的重要因素。

3 尾门系统约束力对解锁条件的影响

某车型尾门锁结构如图2所示，其工作原理为：车辆发出解锁信号后，尾门锁驱动电机通过蜗轮蜗杆传动装置驱动解锁推动杆向外运动，解锁推动杆推动棘爪旋转，从而使棘轮与棘爪脱离啮合状态，棘轮旋转释放锁扣从而使尾门解锁[3～4]。由于棘爪回位弹簧、棘轮回位弹簧以及棘轮与棘爪之间滑动摩擦力的存在，当电机解锁力不足以推动棘爪旋转并与棘轮脱离啮合时，则会出现解锁失效的情况。棘爪回位弹簧与棘轮回位弹簧的力为尾门锁机构的固有属性，不受尾门系统条件的影响，而棘轮与棘爪之间的滑动摩擦力大小则主要由尾门系统约束力F2决定。

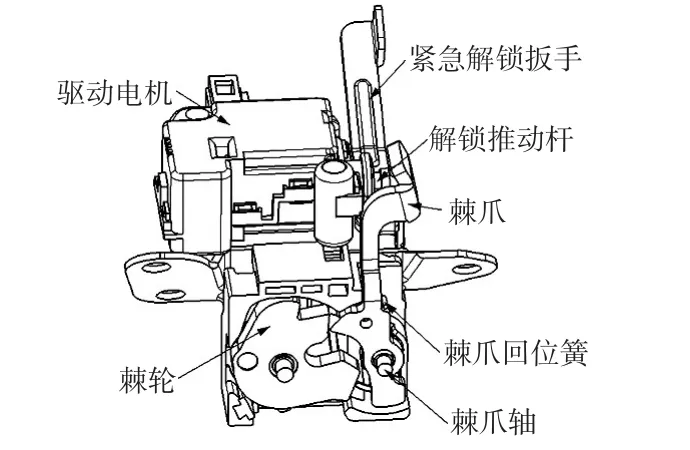
图2 某车型尾门锁结构示意

3.1 系统约束力对棘轮棘爪摩擦力的影响

对棘轮与棘爪的相对运动进行分析，如图3所示，在棘轮与棘爪的啮合状态下，棘轮处于以棘轮旋转轴为轴线的力矩平衡状态：

式中，Fn为棘轮与棘爪间的正压力；Ln1为Fn以棘轮旋转轴为轴线的力臂；Ln2为F2以棘轮旋转轴为轴线的力臂；ML为棘轮回位弹簧以棘轮旋转轴为轴线的回位力矩，属于尾门锁固有属性。

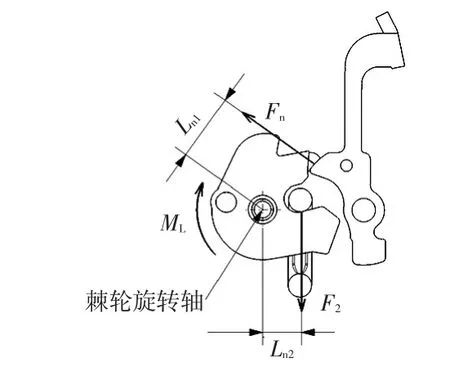
图3 棘轮受力分析

根据滑动摩擦力公式计算可得棘轮与棘爪之间滑动摩擦力为：

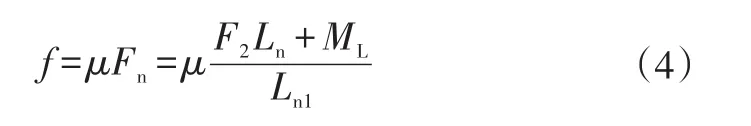
式中，μ为棘轮与棘爪之间的滑动摩擦因数。

在锁体结构保持不变的情况下，Ln1、Ln2、μ及ML均为锁机构的固有属性，系统条件约束力F2是影响锁机构内部棘轮与棘爪之间滑动摩擦力f的外部因素，F2越大，则f越大。

3.2 系统约束力对解锁条件的影响

在解锁推动杆推动棘爪旋转的过程中，需克服棘爪回位弹簧的阻力以及棘爪与棘轮啮合面的滑动摩擦力f才能顺利解锁，如图4所示，因此，可解锁的条件为：

式中，F7为电机推动杆输出力；L7为F7以棘爪旋转轴为轴线的力臂；Lf为滑动摩擦力f以棘爪旋转轴为轴线的力臂；MZ为棘爪回位弹簧以棘爪旋转轴为轴线的回位力矩，属于尾门锁的固有属性。

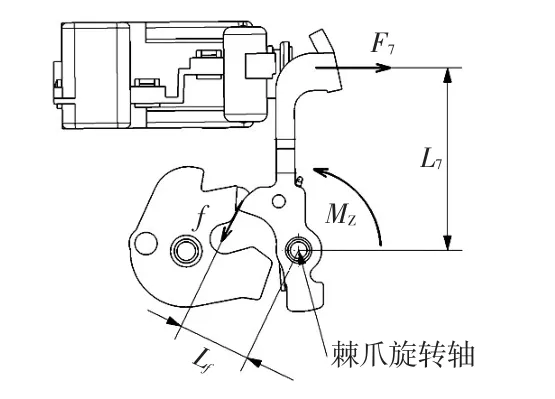
图4 棘爪受力分析

将式（4）带入式（5）可得可解锁条件为：

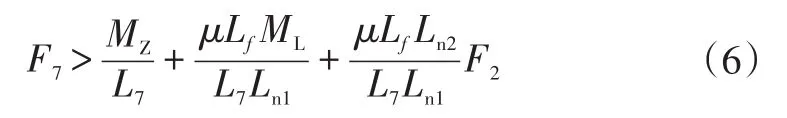
当锁结构一定时，MZ、L7、μ、Lf、ML、Ln1及Ln2均为定值，令，则式（6）可表示为：

系数A与系数k均为与锁结构相关的常数，因此，系统约束力F2是决定解锁能否实现的系统参数，将式（2）带入式（7）可将解锁条件转换为：

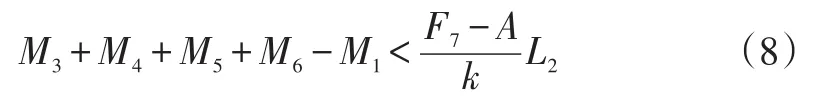
当系统约束力矩M3+M4+M5+M6-M1足够大时，电机推动杆推力F7不足以克服棘爪回位簧的阻力以及棘爪与棘轮啮合面的滑动摩擦力f，解锁条件无法满足，则电机驱动解锁失效。

4 尾门电动解锁后开启可行性计算

在可解锁条件式（8）满足的情况下，锁机构的棘爪释放棘轮解锁，若此时尾门系统支撑力矩与棘轮回位弹簧对尾门的支撑力矩之和不足以克服尾门的重力力矩将尾门弹起，则在棘爪回位弹簧的作用下，尾门锁棘轮与棘爪会重新啮合，导致尾门无法打开，其受力分析如图5所示。

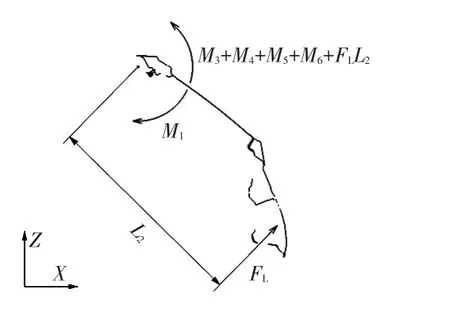
图5 尾门开启可行性受力分析

则尾门锁电动解锁后尾门可开启的条件为：

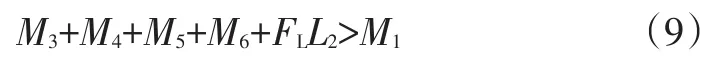
式中，FL为尾门锁棘轮释放后，棘轮回位弹簧作用于锁扣的弹力；FLL2为棘轮回位弹簧以尾门铰链为旋转轴线对尾门的支撑力矩。

将式（8）与式（9）进行组合可得：

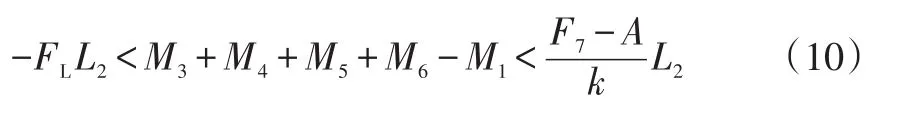
则式（10）为尾门锁可顺利解锁使棘轮棘爪脱离啮合状态并将尾门弹离关闭位置的充分必要条件。

5 系统约束力的修正

考虑车辆的制造公差因素以及环境影响因素，计算过程中需对系统约束力进行修正。

5.1 尾门重力力矩M1的修正

5.1.1 尾门重力变化的修正

在冬季，尾门积雪结冰后会导致尾门质量的增加，从而导致重力力矩M1增大；此外，低配置车型因尾门内饰板简化以及无后风窗玻璃刮水器等因素会导致尾门质量较高配车型小。综合这两方面因素，计算可得尾门重力最小值Gmin与最大值Gmax。

5.1.2 尾门重力力臂变化的修正

图6所示为车辆在驻坡情况下尾门重力力臂变化情况，在下坡驻坡情况下，重力力臂，此时L′1＞L1，在上坡驻坡情况下，重力力臂，此时L″1＜L1。

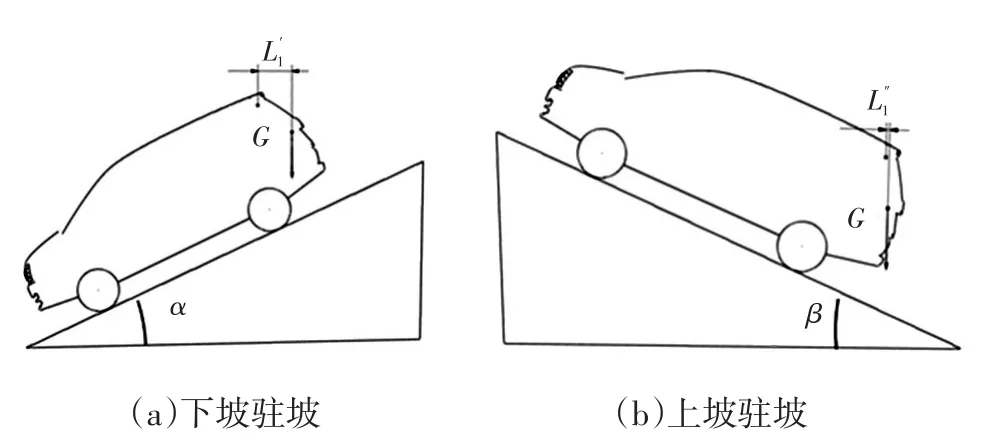
图6 驻坡情况下尾门重力力臂变化情况

综合重力及其力臂两方面的修正，可得尾门重力力矩的最小值为M1min=GminL″，最大值为M1max=GmaxL′。带入式（10）分析可知：重力力矩M1较大有利于尾门实现电动解锁，但是不利于解锁后尾门的开启；M1较小有利于尾门解锁后的开启，但是不利于实现电动解锁。

5.2 尾门缓冲块支撑力矩M3的修正

在尾门关闭状态下，缓冲块处于压缩状态，此时温度对其力学性能的影响效果是在一定压缩变形量条件下的。模拟实车状态，对某车型尾门缓冲块在不同环境温度与不同压缩量下的压缩力进行测试，考虑车辆实际使用过程中的温度情况，选取-20℃模拟冬季低温工况，选取60℃模拟夏季高温日晒工况。

在环境温度箱内不同的设定温度下，采用电子压缩试验机对尾门缓冲块进行不同程度的压缩，保持设定温度以及压缩量30 min后读取压缩力值如表1所示。

由表1可知，在相同温度下，缓冲块压缩力随压缩量的增大而增大，在相同压缩量条件下，该缓冲块在0℃时的压缩反力最大，这是缓冲块材质的回弹性变化与硬度变化共同导致的，在-20℃低温条件下橡胶的回弹性变差导致缓冲块压缩变形后压缩反力减小，在60℃高温条件下橡胶的硬度变小导致缓冲块的压缩反力减小。新车型开发过程中应对具体应用的缓冲块进行实际测量后再取值计算。

在车辆的装配过程中，为了保证尾门与侧围的间隙与面差，需对铰链安装位置、尾门锁扣安装位置以及缓冲块的干涉量进行调整，使得尾门缓冲块的实际压缩量偏离设计状态。例如，某车型缓冲块设计状态压缩量为3 mm，按照制造装配的工艺水平，实际车辆装配状态下缓冲块的压缩量控制在2～4 mm之间，因此，表1中2 mm压缩量、60℃温度条件下的压缩力37.1 N为该缓冲块在实车状态下支撑力可能达到的最小值，4 mm压缩量、0℃温度条件下的压缩力140.5 N为该缓冲块在实车状态下支撑力可能达到的最大值。根据压缩力最小值与最大值计算可得尾门缓冲块以铰链为轴线对尾门的最小支撑力矩M3min与最大支撑力矩M3max。

5.3 尾门限位块支撑力矩M4的修正

尾门限位块在设计状态无压缩量，通常设计预留1 mm间隙进行容差。但是，加入M4的计算会扩大解锁条件的适用范围，有利于满足更严苛工况下的解锁可靠性要求，因此，计算极限装配公差条件下限位块0.5 mm压缩量的支撑力矩M4作为尾门限位块的最大支撑力矩。

在环境温度箱内不同的设定温度下，模拟实车装配状态，对某车型尾门限位块在不同温度下保持0.5 mm压缩量30 min后读取压缩力值如表2所示。

表2 不同温度下限位块0.5 mm压缩量的压缩力

由表2可知，尾门限位块在极限公差0.5 mm压缩量条件下最大压缩力为0℃时的55.1 N。尾门限位块压缩状态如图7所示，则尾门单侧限位块对尾门支撑力矩的最大有效作用力为：

因此可得尾门限位块对尾门的最小支撑力矩M4min=0与最大支撑力矩M4max。

5.4 尾门气弹簧支撑力矩M5的修正

由于尾门的装配公差通常在尾门过关2 mm至欠关1 mm之间，而该公差尺寸对尾门气弹簧在尾门关闭位置的作用力及其力臂影响很小，只需考虑温度对气弹簧的力学性能影响即可。某车型尾门气弹簧支撑力在不同温度下的变化如图8所示，高温条件下气弹簧缸体内气体膨胀导致支撑力增大，低温条件下缸体内气体收缩导致支撑力减小[5～6]。分别以高、低温条件下的气弹簧力计算得到尾门关闭状态气弹簧对尾门的最大支撑力矩M5max与最小支撑力矩M5min。

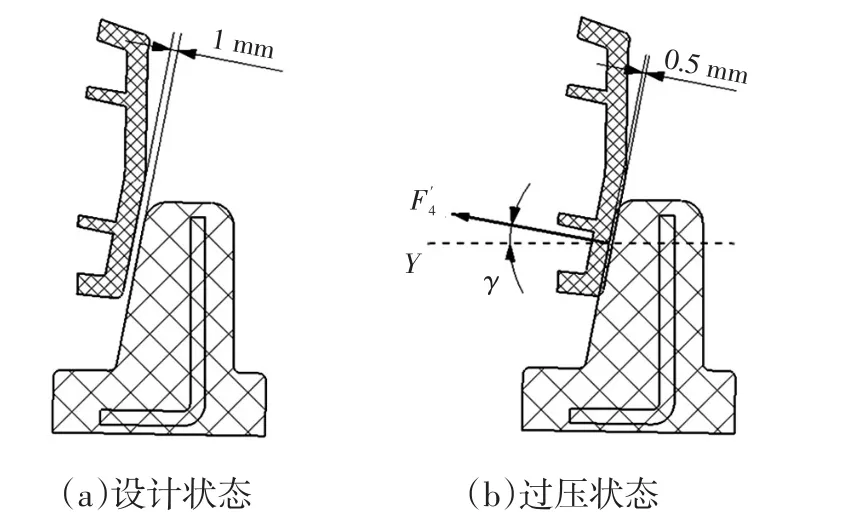
图7 某尾门限位块压缩状态示意

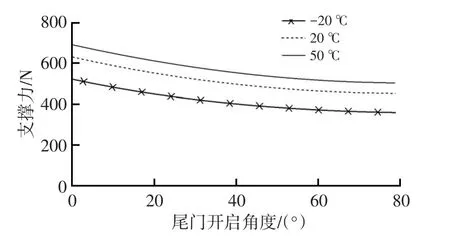
图8 不同温度下某尾门气弹簧支撑力曲线

5.5 尾门密封条支撑力矩M6的修正

模拟实车状态，将尾门密封条制作成100 mm长的样件进行压缩测试。在环境温度箱内不同的设定温度下，采用电子压缩试验机对密封条进行不同程度的压缩，保持设定温度以及压缩量30 min后读取压缩力值。

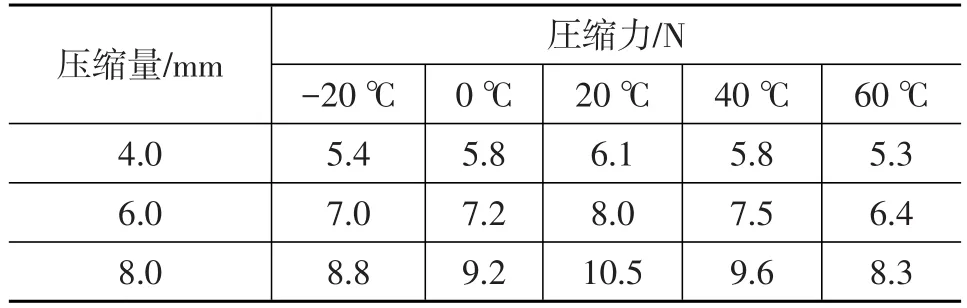
表3 不同温度与压缩量条件下的密封条压缩力

由表3可知，在相同的测试温度下，尾门密封条的压缩力随压缩量的增大而增大，在相同的压缩量条件下，受密封条回弹性与硬度变化的影响，在20℃时密封条的压缩反力最大，其机理与缓冲块相似。

同样，尾门密封条受尾门装配间隙与面差的影响，实际装配状态可能会出现±2 mm的公差，即设计状态下压缩量为6 mm，实际装车时可能会出现4～8 mm之间的压缩量。因此，4 mm压缩量、60℃温度条件下的压缩力5.3 N为该密封条在实车状态下压缩力可能出现的最小值，8 mm压缩量、20℃温度条件下的压缩力10.5 N为该密封条在实车状态下压缩力可能出现的最大值，根据压缩力最小值与最大值计算可得尾门密封条以铰链为轴线对尾门的最小支撑力矩M6min与最大支撑力矩M6max。

5.6 系统约束力的极限修正

由式（10）可知：系统约束力矩F2L2越小，越有利于尾门电动解锁的实现，但不利于电动解锁后尾门开启的实现；F2L2越大，越有利于尾门解锁后开启条件的实现，但不利于尾门电动解锁条件的实现。因此，设计时以F2L2的最大值来验证尾门的可解锁条件式（8），以F2L2的最小值来验证尾门的可开启条件式（9），有利于尾门满足在各种工况下的解锁与开启可行性。

但各零件的极限支撑力矩并非出现在同一环境条件下，由式（10）可知，计算时取F2L2=M3+M4+M5+M6-M1的极限值进行匹配的算法是对解锁条件以及开启条件安全系数的放大，因此，系统约束力的最终修正状态以各种组合工况下极限值进行计算。

因此，解锁条件式（8）的极限修正为：

Research on the Effect of the Tail Gate Binding Force on the Unlocking Condition

Li Chaoshuai,Lin Sen,Yu Bo,Li Ruisheng
（Brilliance Automotive Engineering Research Institute,Shenyang 110000）

In order to solve the problem of the lock mechanism failure caused by the change of the closure system during the development process of a new vehicle,a mathematical model for the tail gate system was established.The influence factors of the system such as the seal of the tail gate,the gas spring and the buffer block were converted to the binding force.The influence of the binding force of the tail gate system on the unlocking condition was analyzed in combination of the operating principle of tail gate lock internal structure,and a refined matching calculation method for the binding force and the unlocking condition of the tail gate system was presented.At the same time,the external factors, which need to be considered in the calculation process were put forward,and the calculation parameters were modified to meet the functional stability of the tail gate under various conditions.

Tail gate system,Binding force,Unlocking condition,Matching calculation

尾门系统 约束力 解锁条件 匹配计算

U463.85+4

A

1000-3703（2016）12-0037-05