页岩储层裂缝渗透率动态变化研究

孙同英 陈永昌 厉亚明 刘运霞 刘银山

(1. 中原油田采油二厂， 河南 濮阳 457006； 2. 中国地质大学(北京)能源学院， 北京 100083；

页岩储层裂缝渗透率动态变化研究

孙同英1，2陈永昌1厉亚明1刘运霞1刘银山3

(1. 中原油田采油二厂， 河南 濮阳 457006； 2. 中国地质大学(北京)能源学院， 北京 100083；

3. 陕西延长石油集团研究院， 西安 710075)

在页岩气藏开采过程中，页岩储层的渗透性随孔隙压力的降低而发生变化。分析有效应力效应、基质收缩效应和克林肯伯格效应对页岩渗透率的影响，在此基础上建立页岩裂缝渗透率动态变化模型，综合研究页岩储层裂缝渗透率的动态变化规律。研究结果表明：开采初期，页岩储层压力降低，有效应力的影响显著；开采中期，当页岩储层压力降低到气体临界解吸压力后，页岩吸附气不断解吸，基质收缩效应开始影响裂缝的渗透性；开采后期，在低压环境下克林肯伯格效应成为主导影响因素。

页岩； 裂缝渗透率； 有效应力； 基质收缩效应； 克林肯伯格效应

页岩渗透性是研究页岩内部气体运移的基本参数之一。在页岩气排采过程中，页岩渗透性除了受页岩自身原始孔隙发育程度和埋深的影响外，同时还受到有效应力效应、基质收缩效应和克林肯伯格效应的综合影响。页岩内部发育大量微裂缝，裂缝的渗透性严重影响着页岩气的产能。国内外学者就页岩渗透性变化影响因素作了很多研究。本次研究是在其他相关研究的基础上，建立裂缝渗透率动态变化模型，综合分析有效应力效应、基质收缩效应和克林肯伯格效应对页岩裂缝渗透性的影响规律。

1 有效应力效应对页岩裂缝渗透率的影响

随着页岩气的持续开采，页岩储层中的流体不断排出，储层压力随之减小，而上覆压力则近似不变，页岩储层受到的有效应力逐渐增大，储层受压导致物性降低。这种效应就是有效应力效应。

裂缝与基质岩块刚度差距较大，裂缝受到应力的作用时易发生变形，裂缝包裹的基质岩块不易变形。图1所示为页岩表征体积单元示意图，裂缝宽度为d，基质长度为s。

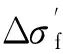
(1)

(2)

图1 页岩表征体积单元示意图

在有效应力的作用下，表征体积单元中裂缝和基质岩块的变化量分别通过式(3)、(4)来计算：

(3)

(4)

假设表征体积单元的边界条件不变，表征体积单元大小不发生变化，则有式(5)：

Δuf+Δum=0

(5)

联立式(3)、(4)和(5)得到式(6)：

(6)

假设表征体积单元内气体压力均匀扩散，即基质岩块和裂缝中的压力变化相同。如式(7)所示：

Δpf=Δpm=Δp

(7)

压力变化造成的裂缝变化量为：

(8)

在此忽略湍流，假设气体仅在裂缝中流动，计算图1模型中裂缝的初始渗透率[1-4]：

(9)

那么裂缝变化后的渗透率公式为：

(10)

将式(8)代入式(10)，得到有效应力效应影响下的页岩裂缝渗透率变化公式：

(11)

毕奥系数可用于表征孔隙压力变化所致的岩石变形数量级，它与骨架的相对刚度及固体成分的刚度相关[5]。毕奥系数可通过式(12)计算：

α=1-K/Ks

(12)

其中裂缝刚度与其所受有效应力之间呈正相关[6-8]，有效应力越大，裂缝刚度增大。这是因为在有效应力作用下，裂缝趋于闭合，裂缝空间缩小。裂缝的刚性系数与有效应力的线性关系如式(13)所示：

(13)

裂缝的有效刚度远小于固体部分的刚度，所以裂缝的毕奥系数约等于1，根据定义可知基质的毕奥系数小于1。从式(13)可以看出，随着表征体积单元内压力降低，有效应力效应导致裂缝渗透率下降。

2 基质收缩效应对页岩裂缝渗透率的影响

基质收缩效应是指当页岩储层压力降低到气体临界解吸压力后，页岩内的吸附气不断解吸，脱离吸附介质表面，孔隙空间得到扩展，即基质产生收缩，使得气体流动性变好。

假设页岩内吸附气解吸过程服从Langmuir等温吸附方程，对吸附气解吸导致的表征体积单元应变进行均一化处理，得到式(14)：

(14)

通过式(15)，计算表征体积单元中基质岩块体积：

Vm=s3

(15)

在三维空间体系中，吸附气解吸导致的基质体积收缩等于裂缝体积的增加，则有式(16)：

ΔVf=s2Δds=Vmεs

(16)

那么，由式(10)得出式(17)，即气体解吸引起裂缝渗透率变化的计算公式：

(17)

联立式(13)、(14)、(15)，整理得到吸附气解吸导致的裂缝渗透率变化公式：

(18)

对于本次建立的裂缝模型，裂缝孔隙度可由式(19)计算：

(19)

如果裂缝的孔隙度和裂缝空间大小已知，那么式(17)可变换为式(20)：

(20)

从式(20)中看出，随着压力降低，气体解吸导致基质收缩，对页岩裂缝渗透性的影响是正向的，裂缝渗透性变好。

3 克林肯伯格效应对页岩裂缝渗透率的影响

克林肯伯格效应(也称滑脱效应)，是指在低压环境时低渗储层内的气体分子与流通通道的壁面发生碰撞，而使气体流速加大的现象。页岩中的气体流通通道为微小孔隙，多为微米级，甚至纳米级[9-12]，气体流速很低，气体分子容易产生滑脱。为了增加气体流速，我们需要考虑微孔隙中的气体滑脱现象对页岩渗透性的影响。

Klinkenberg在考虑气体滑脱效应的基础上，定义式(21)所示气测渗透率公式[13]：

(21)

(22)

从式(22)中可看出，压力越小，滑脱效应对渗透率变化的影响越大。对于致密页岩储层而言，在低压环境下，滑脱效应的影响更大，在一定程度上改善了页岩裂缝的渗透性。

4 渗透率综合模型分析

4.1 模型的建立

在研究页岩裂缝渗透率变化特征时，必须同时考虑上述效应的综合影响，避免造成大的误差。此次所建渗透率动态变化数学模型耦合了有效应力效应、基质收缩效应和克林肯伯格效应：

(23)

式中，A、B、C分别表示有效应力效应、基质收缩效应和克林肯伯格效应对页岩渗透率的影响因子。各影响因子计算如下：

图2所示为不同效应下的页岩裂缝渗透率动态变化示意图。

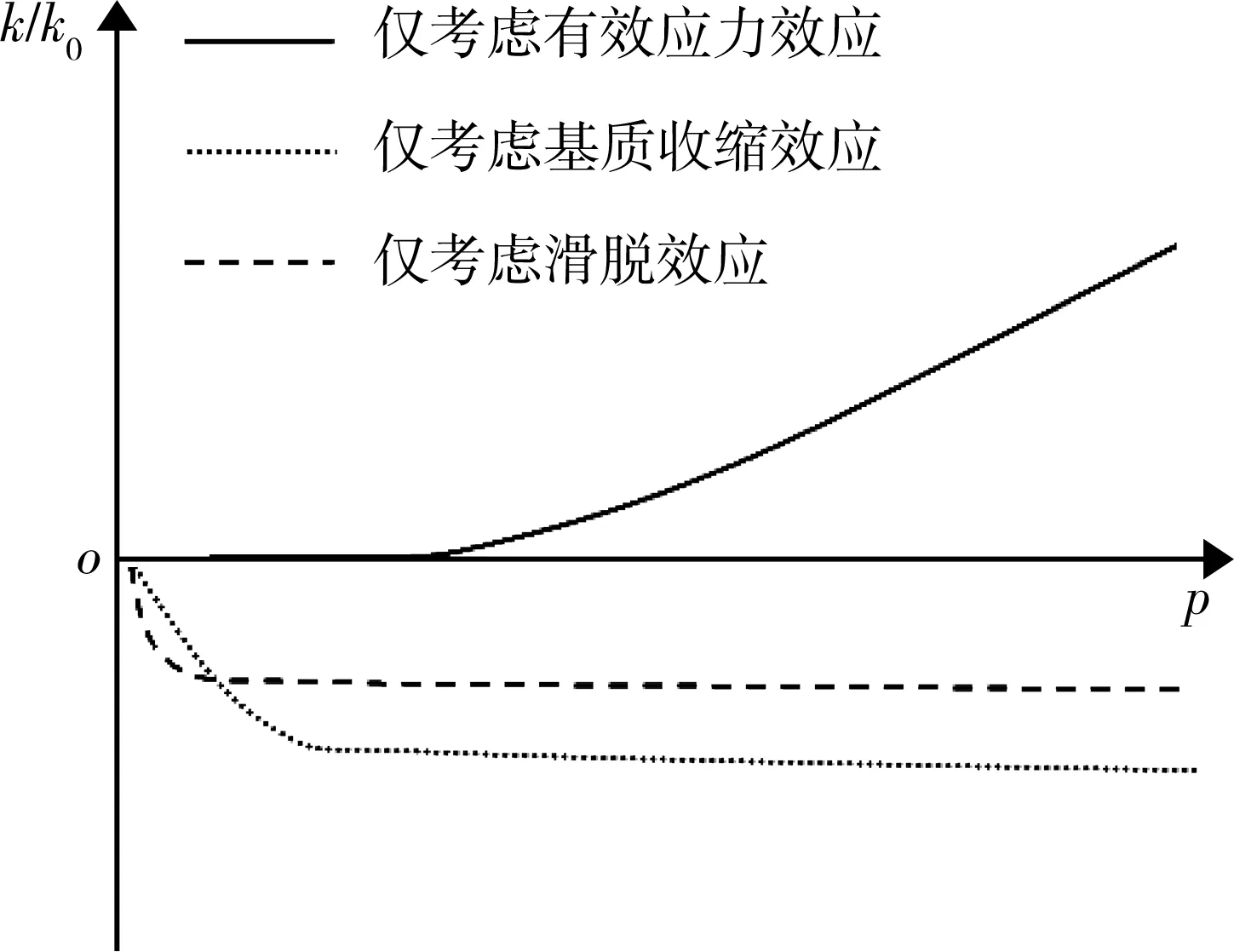
图2 不同效应下的页岩裂缝渗透率动态变化示意图

在页岩储层孔隙压力变化初期，有效应力效应明显；当孔隙压力低于吸附气临界解吸压力后，吸附气开始解吸，页岩基质收缩效应产生影响；在低压环境下，页岩微孔隙中的滑脱效应的影响突显出来。对中后期页岩裂缝渗透性的研究应综合考察3种效应的整体影响，才能得到接近真实变化规律的研究结果。

4.2 算例分析

对模型计算结果与实验结果进行拟合，对比模型的准确适用性，分析页岩储层裂缝渗透率变化规律。模型参数赋值见表1。模型计算结果与实验数据[14]对比结果见图3。

表1 模型参数赋值

图3显示，模型的计算结果和实验数据动态变化的拟合度较高，说明模型的适用具有可行性。根据模拟结果及实验数据结果来看，孔隙压力的降低会造成页岩裂缝渗透性的极大损害。尤其是在孔隙压力变化前期(80～120 MPa)，裂缝渗透率快速下降，反映出有效应力效应的较强影响。在低压条件下，由于基质收缩效应和滑脱效应的影响，气体解吸导致裂缝空间增大和裂缝中气体流速增大，相对改善了裂缝渗透性。

图3 模型计算结果与实验数据对比

在页岩气藏的开发过程中，需要建立合理的工作制度，控制页岩气藏的压力变化幅度，延长气藏压力衰减时间，尽量减小页岩裂缝的渗透率降低幅度，维持页岩储层有效裂缝导流能力，实现气藏最大程度的开发。

5 结 语

全球页岩气资源量巨大，我国页岩气资源也比较可观，研究页岩储层渗透性的变化规律有助于实现页岩气藏的有效开发。

页岩储层渗透性受有效应力效应、基质收缩效应和克林肯伯格效应3种效应的影响。在储层孔隙压力变化初期，有效应力的影响显著；当孔隙压力低于气体临界解吸压力时，基质收缩效应开始产生影响；在后期低压环境下，气体滑脱效应的影响突显。本次研究所建综合模型能反映3种效应下的页岩储层裂缝渗透率变化特征。

页岩储层裂缝渗透性制约页岩气藏的开发效果，合理控制页岩储层压力变化，减少页岩储层裂缝渗透率降低幅度至关重要。

文中符号说明：

k—— 页岩裂缝渗透率，μm2；

k0—— 裂缝初始渗透率， μm2；

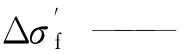
αf—— 裂缝有效应力系数，无量纲；

αm—— 基质Biot有效应力系数,无量纲；

Δp—— 表征体积单元的压力变化，MPa；

δij—— 克罗内克张量，取1；

Kf—— 裂缝刚度系数，GPa/m；

Em—— 基质矩阵模量，GPa；

Δuf—— 裂缝在应力方向上的矢量变化，μm；

Δum—— 基质在应力方向上的矢量变化，μm；

d—— 裂缝缝宽，μm；

s—— 表征体积单元边长，μm；

ΔVf—— 裂缝体积变化，μm3；

ΔVm——基质体积变化，μm3；

εs—— 基质收缩应变；

εL—— Langmuir应变；

φ—— 裂缝孔隙度，%；

pL—— Langmuir压力，MPa；

p0—— 初始压力，MPa；

c—— 比例系数，等于1；

λ—— 气体分子平均自由程，μm；

b—— 滑脱因子。

[1] BAI M, ELSWORTH D.Modeling of Subsidence and Stress-dependent Hydraulic Conductivity for Intact and Fractured Porous Media [J].Rock Mechanics and Rock Engineering,1994,27(4):209-234.

[2] OUYANG Z,ELSWORTH D.Evaluation of Groundwater Flow into Mined Panels [J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1993,30(2):71-79.

[3] WANG S G,ELSWORTH D,LIU J S.A Mechanistic Model for Permeability Evolution in Fractured Sorbing Media [J].Journal of Geophysical Research,2012,117:6205.

[4] LIU J,ELSWORTH D.Three-Dimensional Effects of Hydraulic Conductivity Enhancement and Desaturation Around Mined Panels[J].International Journal of Rock Mechanics & Mining Sciences,1997,34(8):1139-1152.

[5] NUR A ,BYERLEE J D.Exact Effective StressLaw for Elastic Deformation of Rock with Fluids[J].Journal of Geophysical Research,1971,76 (26):6414-6419.

[6] WALSH J B ,GROSENBAUGH M A.A New Model for Analyzing the Effect of Fractures on Compressibility[J].Journal of Geophysical Research,1979,84 (B7):3532-3536.

[7] TAO Q F,AHMAD G,CHRISTINE A.A Fully Coupled Method to Model Fracture Permeability Change in Naturally Fractured Reservoirs[J].International Journal of Rock Mechanics & Mining Sciences,2011,48:259-268.

[8] ALIREZA B ,JING L R.Stress Effects on Permeability in a Fractured Rock Mass With Correlated Fracture Length and Aperture[J].International Journal of Rock Mechanics & Mining Sciences,2008,45:1320-1334.

[9] CLARKSON C R ,SOLANO N,BUSTIN R M,et al.Pore Structure Characterization of North American Shale Gas Reservoirs Using USANS/SANS,Gas Adsorption,and Mercury Intrusion[J].Fule,2013,103:606-616.

[10] DANIEL J K,ROSS,BUSTIN R M.The Importance of Shale Composition and Pore Structure Upon Gas Storage Potential of Shale Gas Reservoirs[J].Marine and Petroleum Geology,2009,26:916-927.

[11] 杨峰,宁正福,胡昌蓬,等.页岩储层微观孔隙结构特征[J].石油学报,2013,34(2):301-311.

[12] 陈尚斌,夏筱红,泰勇,等.川南富集区龙马溪组页岩气储层孔隙结构分类[J].煤炭学报，2013,38 (5):760-765.

[13] KLINKENBERG L J.The Permeability of Porous Media to Liquids and Gases[J].Socar Proceedings,1941,2(2):200-213.

[14] DONG J J,HSU J Y,WU W J,et al.Stress-Dependence of Permeability and Porosity of Sandstone and Shale From TCDP Hole-A[J].International Journal of Rock Mechanics & Mining Sciences,2010,47:1141-1157.

A Dynamic Model of Shale Fracture Permeability

SUNTongying1,2CHENYongchang1LIYaming1LIUYunxia1LIUYinshan3

(1. 2nd Oil Factory of Zhongyuan Oil Field, Puyang Henan 457006, China;2. Energy Institute of China University of Geosciences, Beijing 100083, China;3. Research Institute of Yanchang Petroleum (GROUP) Co., Xi′an 710075, China)

In the process of exploiting shale gas reservoirs, the permeability of shale decreases with the decrease of pore pressure. On the basis of considering the effects of effective stress, matrix shrinkage and klinkenberg effect, we propose a new dynamic change model of fracture permeability to comprehensively study the dynamic variation law of fracture permeability of shale reservoir. The results suggest that the impact of effective stress is obvious at the early time, when the pressure reduces to the critical desorption pressure; with the desorption of adsorbed gas, the matrix shrinkage effect affects the permeability; and at the late stage, the klinkenberg effect becomes the dominant factor.

shale rock; fracture permeability; effective stress; matrix shrinkage; klinkenberg effect

2016-03-07

国家科技重大专项“泥岩内油气储集状态及渗流机理研究”(2011ZX05009-006);中央高校基本科研业务基金项目“非常规油气储层特征及开采机理研究”(35832015034)

孙同英(1987 — )，男，硕士，助理工程师，研究方向为低渗储层渗流动态、资源储量评价。

TE311

A

1673-1980(2016)06-0005-04