农用车辆悬架的干扰解耦H∞观测器设计

王 刚

（贵州理工学院 机械工程学院，贵州 贵阳 550003）

0 引言

农用车辆经常工作在路面环境恶劣的工况下，由于长时间的振动会造成驾驶人员的疲劳和疼痛，对车辆进行主动减振是有意义的研究工作[1]。由于H∞控制易于处理该类型的振动控制问题，已经取得了大量的研究成果，该方法能在保证时域约束的同时，最大化的提高悬架的舒适性[2-5]。

从关于H∞控制的文献中可看出，所设计的控制器几乎都依赖于全部或部分状态量的测量[6，7]。然而在实际应用中，由于传感器类型及安装位置的限制，状态变量仅部分可测或全不可测，以文献[8]的松本汽车为例，仅簧载与非簧载质量处的加速度可测。导致在实际应用中，即使配备了主动悬架的汽车也难以构成相应的闭环系统。考虑到目前针对农用车辆主动悬架的观测器设计研究较为少见，因此有必要研究在状态量不可测时，如何实现车辆主动悬架的闭环控制策略。本文提出了一种基于干扰解耦的H∞观测器设计方法，最后通过一个数值实例验证了所提方法的有效性。

1 模型建模与问题描述

考虑到大多数文献均以1/4悬架模型为研究对象，为了便于说明该方法的有效性，这里亦采用如图1所示的基于状态观测器的1/4车悬架模型。图中ms，mu分别代表簧载与非簧载质量，ks，cs为主动悬架的刚度与阻尼系数，ku为轮胎的可压缩刚度系数，xs，xu分别为簧载与非簧载质量的垂直位移，q为路面不平度激励为观测器估计的状态变量，u为主动控制力，x¨s，分别为加速度计测量的加速度信息。

在大多数文献中，均取系统的状态变量为：

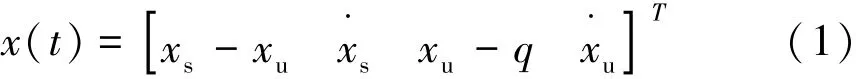
并假定全部或部分状态量可测。而在实际应用当中，限于传感器类型及安装位置的限制，仅簧载与非簧载质量的加速度方便测量。故本文的思路为仅以加速度为已知量，通过设计的状态观测器去估计系统的全部状态变量，并将其应用于悬架的主动控制当中，故定义可测量为

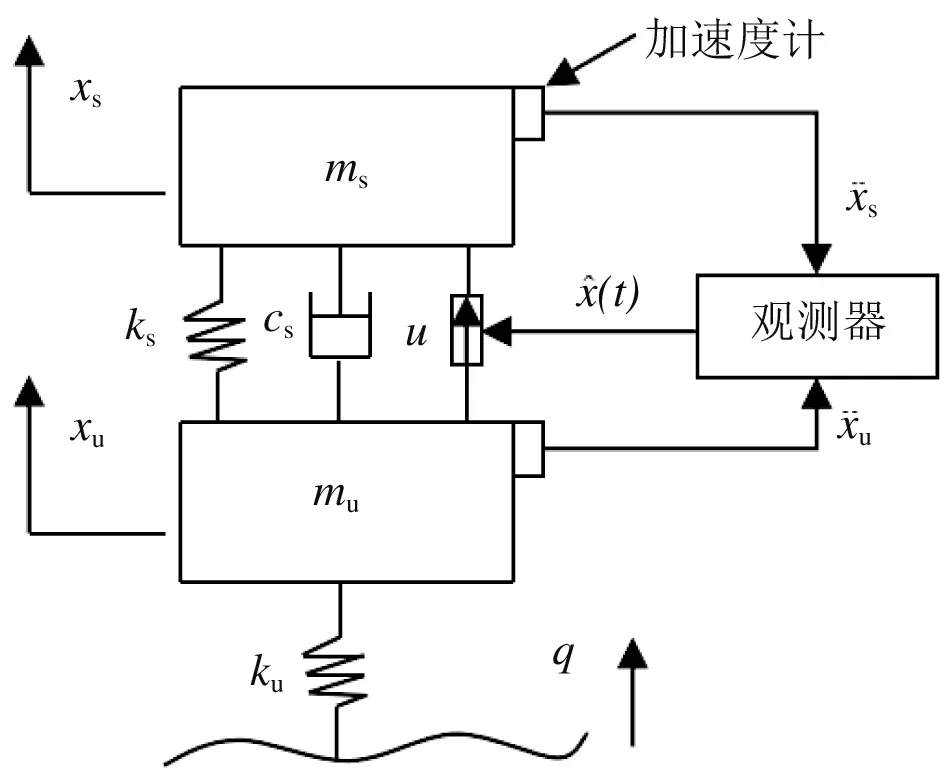
图1 基于状态观测器的1/4车悬架模型

根据状态变量（1），可得系统的状态空间方程：

2 干扰解耦观测器设计

在求出所需的控制器增益矩阵后，便可按如下步骤设计系统的状态观测器。这里取理想情况下的状态反馈作为控制输入，即u（t）=Kx（t），这样不仅可以便于之后的干扰解耦，还可以避免系统的误差积累。将其代入（2）中可得如下的闭环系统：

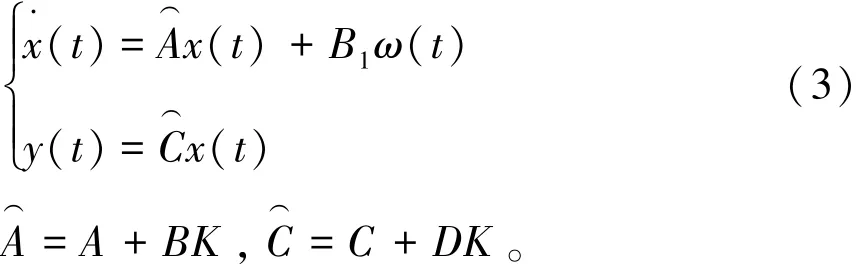
定义所设计的全阶状态观测器形式如下：

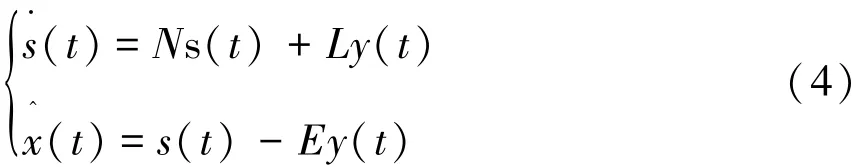
N，L，E为待求的观测器矩阵。观测系统的误差方程为

P B1=0。

由文献[9]可知，虽然可根据条件（1）（2）求解出精确的观测器矩阵，但由于极点配置等问题在实际中难以实现，且当某些矩阵轶条件不满足时，并不存在精确的可行解。故本文考虑采用H∞的方法在保证系统收敛稳定的基础上，最小化干扰对估计量的影响。

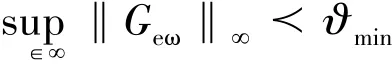
为了求得满足命题1的观测器矩阵，首先对方程（5）进行如下的未知矩阵变换。

根据未知矩阵Λ，上式等价于方程Λ·Θ=Γ，其中

由广义逆性质可知，上式有解的充分必要条件为：

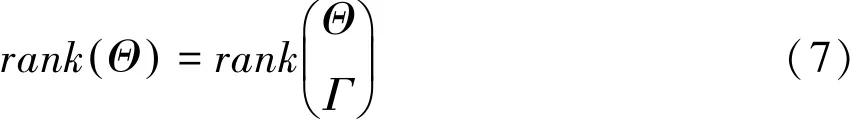
若条件（7）不满足，则命题1中的H∞-观测器不存在。若条件（7）满足，则可解得满足系统收敛稳定的未知矩阵（Λ=Γ Θ＋＋Φ I12-Θ Θ＋），其中Φ为合适维数的任意矩阵，Θ＋为矩阵Θ的广义逆矩阵，由满轶分解可得：

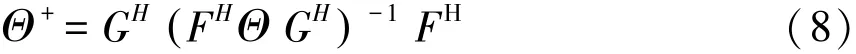
其 中FG=Θ，rank（F）=rank（G）=rank（ Θ）。

从（9）式中可看出，为了满足命题1中的条件，需要设计一个观测器矩阵Φ，使得干扰ω（t）对e（t）的能量增益降低到ϑmin以下。由有界实引理[10]可得如下的推论。

推论1：给定正标量ϑ，对于系统（3）及误差方程（5），若存在对称正定矩阵X及一般矩阵满足如下LMI，则命题1成立。

若推论1有可行解，则相应的观测器矩阵为：

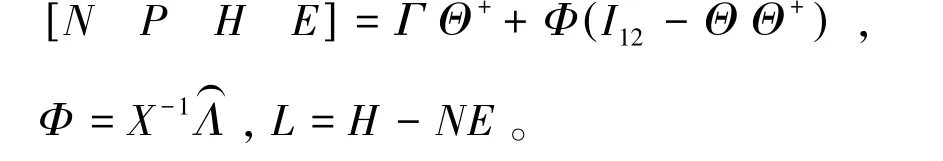
在实际应用中，由于量测噪声的影响，若观测器的极点具有较高的虚部，则会引起系统的振荡与失稳现象。因此这里应用LMI域方法[9]将观测系统的极点配置在如下的梯形区域D内。

应用推论2可将观测系统的极点配置在如图2所示区域内，从而保证系统的鲁棒性。

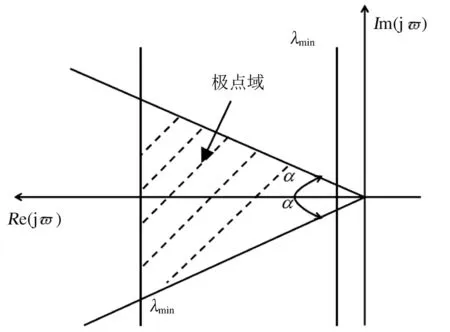
图2 LMI极点域

推论2 ：给定正标量ϑ，对于系统（3）及误差方程（5），若存在对称正定矩阵X及一般矩阵满足如下LMIs，则命题1成立，且观测系统的极点可配置在区域D内。

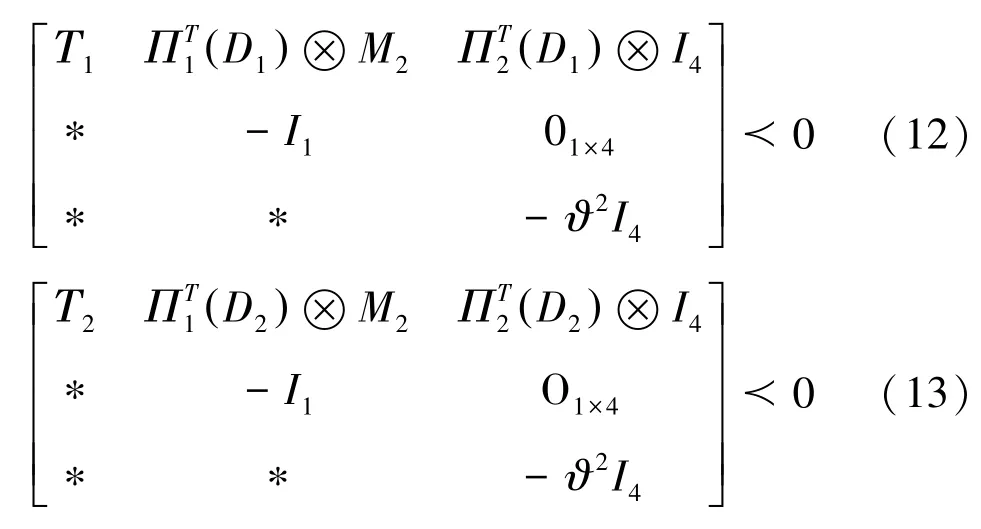
相应的证明过程可参考文献[9]中的LMI域极点配置方法。。

3 数值验证

为了验证所提设计方法的有效性，这里以图1所示的1/4悬架模型为例给出数值验证。悬架模型参数如表1所示。极点配置参数选为α=π/4，λmin=10，λmax=100。

表1 悬架模型参数

根据上述参数，可求出满足系统性能要求的控制器增益矩阵及观测器矩阵。具体步骤如下：

第一步：首先求解有限频域控制器增益矩阵为[3]。

第二步：若参数矩阵轶满足条件（7），表示使系统收敛稳定的未知矩阵存在，进一步可求得广义逆矩阵Θ＋。

应用求出的观测器矩阵，可得干扰对各误差分量的奇异值响应曲线（图3）。从图中可看出干扰对各误差分量的影响情况，其中在0.01-100 Hz范围内的最大能量增益值均小于2.5×10-6，可见该方法具有较小的保守性。

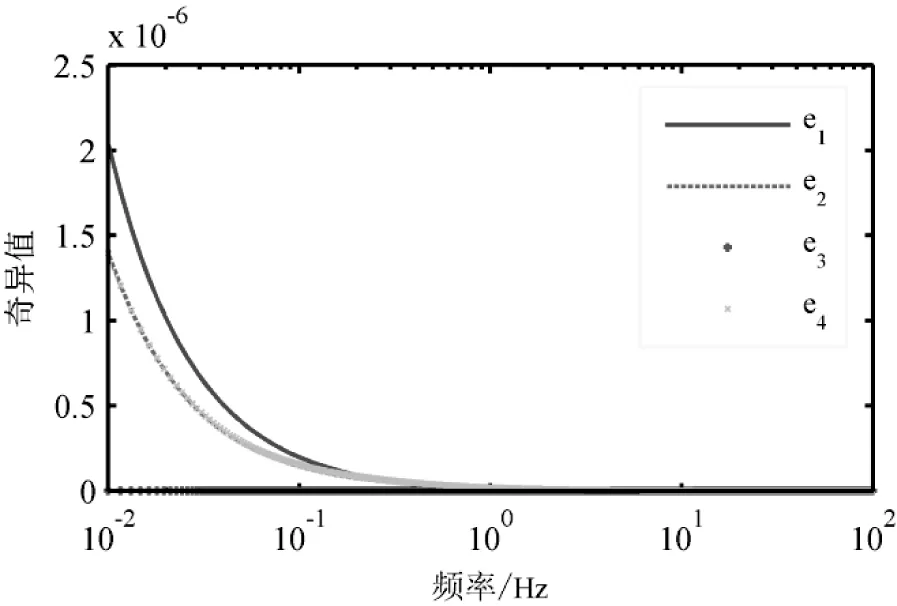
图3 误差e的奇异值响应曲线

为了验证该方法的时域观测情况及控制效果，应用求出的观测器矩阵及控制器增益矩阵进行时域仿真分析。选择如下函数作为路面不平度干扰：

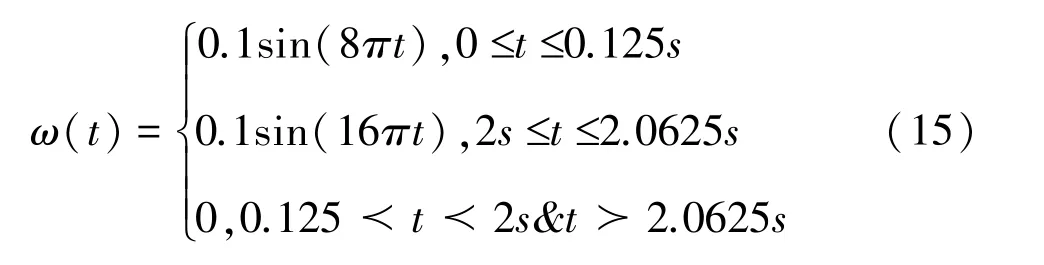
图4 状态观测值

图4为该包块激励下的状态观测量与悬架系统实际状态量的对比曲线，从图中可看出所设计的观测器可以很好的估计实际的状态变量，且误差e的量级均小于10-4。

4 结论

由于在实际的农用车辆悬架主动控制当中，限于传感器的类型及安装位置的不便，状态变量仅部分可测或全不可测，而大多数主动控制方法均依赖于系统的状态变量的测量。针对上述问题，本文提出了一类基于干扰解耦的H∞观测器设计方法，并将其应用于车辆悬架的有限频域多目标控制当中。最后通过数值实例给出了观测器的设计过程，并验证了所提方法的有效性，在包块激励及随机路面激励下，均能将观测误差的量级降低到10-4以下。