一种扩展染色模糊故障Petri网的故障分析方法
凌益琴,苏 艳
(南京航空航天大学 民航学院,南京 210016)
【机械制造与检测技术】
一种扩展染色模糊故障Petri网的故障分析方法
凌益琴,苏 艳
(南京航空航天大学 民航学院,南京 210016)
针对传统故障诊断方法在模拟故障传播及诊断推理过程中存在不确定性等问题,提出一种基于扩展染色模糊故障Petri网的故障诊断分析方法;首先,在采用传统的Petri网模型描述系统故障状态的基础上,引入令牌、库所染色规则,并进一步结合模糊产生式规则与矩阵运算进行故障正反推理,提高模型的容错性;该模型正向推理采用变迁点火判别矩阵实现故障状态的智能评价,反映故障传播特性;逆向推理采用最小割集理论方法进行优先诊断,提供诊断次序,避免诊断的盲目性;最后以气源系统为典型应用对象,验证上述方法的有效性。
扩展染色模糊故障Petri网;染色规则;最小割集;故障诊断;气源系统
随着航空技术的快速发展,民用飞机系统的结构和故障机理越来越复杂,诊断模型很难建立。在实际工程应用中,故障通常体现出模糊性、不确定性、随机性、动态性以及非定量性等特点[1]。针对这些特点,国内外已经建立起多种故障诊断模型描述复杂系统的失效过程,如贝叶斯网络模型[2]、神经网络模型[3]、符号有向图模型(Signed Directed Graph,SDG)[4-5]等。然而,上述诊断模型大都采用传统的数学方法求解,常出现诊断结果准确率不高或者故障遗漏且无法模拟故障传播路径等,无法适应目前的诊断发展趋势。
Petri网具有严格的数学表述方式和直观的图形表达方式以及丰富的系统描述手段和系统行为分析技术,被国内外研究学者应用到故障诊断领域,但传统的Petri网模型不能充分表达故障信息的不确定性和模糊性。为此,杨健维等[6]将Petri网与模糊技术相结合,提出了模糊Petri网(Fuzzy Petri Net,FPN)的建模方法,有效解决了上述问题,但未给出动态推理算法。程学珍等人[7-8]又将模糊Petri网和故障Petri网结合,提出了FFPN(Fuzzy Fault Petri Net,FFPN)的概念,并应用矩阵推理算法对电动机进行故障诊断。这些Petri网模型庞大且复杂,缺乏描述传播特性和传播状态,限制了Petri网直接模拟复杂过程的能力,马良荔等人[9-10]提出了有色Petri网(Color Petri Net,CPN)模型,利用Petri网属性表示系统状态及行为的变化关系,准确地描述系统的产生和传播特性。本文考虑民用飞机系统故障传播的复杂性、动态性特点,将现有的模糊故障Petri网理论和有色Petri网有效地结合起来,提出一种故障信息表达更加完备的扩展染色模糊故障Petri网模型(Color Fuzzy Fault Petri Net,CFFPN)。
1 染色模糊故障Petri网模型
Petri网的基本元素是“库所”和“变迁”,两者用有向弧连接。“库所”描述系统的故障模式,在Petri图中用圆圈表示;“变迁”描述故障模式的变化,在Petri图中用矩形表示;“令牌”(Token)描述故障事件置信度等级,在Petri图中用小黑点表示。扩展染色模糊故障Petri网的基本定义是在传统模糊故障Petri网基础上扩展的,加入了染色规则。
定义1染色模糊故障Petri网定义为一个十二元组:SCFFPN=(P,T,I,O,K,C,M,Ω,α,f,H,U),其中,P={p1,p2,…,pn}(n>0)为有限非空库所结点集合;T={t1,t2,…,tm}(m>0)为有限非空变迁结点集合,t为库所结点;I=P×T为Petri网输入矩阵,反映库所到变迁的映射;O=T×P为Petri网输出矩阵,反映变迁到库所的映射;K={k1,k2,…,kn}为令牌(Token)的有限集合;C为颜色集合;M=(m1,m2,…,mn)T为库所标识分布n维向量;Ω=(ω1,ω2,…,ωn)T为库所权值n维向量,表示输入库所p对变迁规则t的影响;α=(α1,α2,…,αn)T为故障事件置信度n维向量;f={f1,f2, …,fn}为库所底事件模糊故障率的集合;H=(λ1,λ2,…,λm)T为变迁规则阈值m维向量,元素λj为变迁规则tj点火的阈值;U=diag(μ1,μ2,…,μm)为变迁规则置信度矩阵,元素μj为变迁规则tj的阈值[10]。CFFPN模型的图形化表示见图1,染色规则如下:
1) 令牌(Token)具体染色规则见表1。
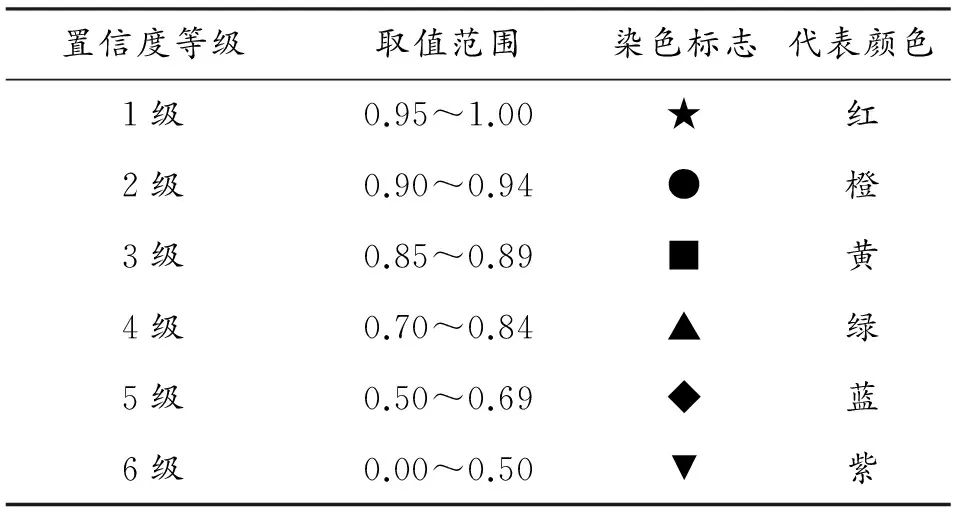
表1 Token染色规则
2) 库所染色规则。故障根本原因(故障征兆),用“◎”表示该库所的状态。例如是否含有Token,即是否发现故障征兆,由在线监测设备或专业人员知识获得,如图1的p1,p2。
故障中间原因,用“○”表示该库所的状态,如图1的p3。
故障最终状态,表示系统分析中所关心的结果状态,用“●”表示该库所的状态,如图1的p4。
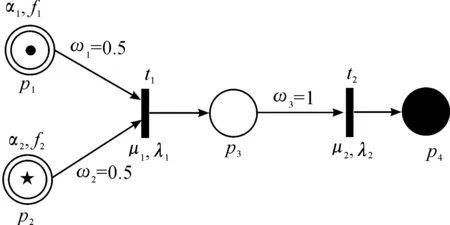
图1 CFFPN模型的图形化表示
2 基于CFFPN模型的故障推理算法实现
本文充分利用Petri网的并行计算和矩阵运算能力,并根据Petri网的可达性进行正反推理。其中正向推理主要是根据测试或专家知识预测可能出现的故障征兆信息,用于监测故障信息比较完备的在线故障诊断问题;反向推理则是根据已经发生的故障现象寻找导致此故障的根本原因,需进行模糊推理,用于监测故障信息不太充分的离线故障诊断。基于CFFPN模型的故障推理算法如图2所示。
在故障模型推理算法前,为了更好地表示各矩阵推理运算,鉴于文献[11],引入算法中要用到的算子,定义如下:
1) 取大算子⊕:C=A⊕B,A、B和C均为m×n矩阵,则cij=max(aij,bij),其中i=1,2,…,m,j=1,2,…,n。
2) 取小算子∧:C=A∧B,A、B和C均为m×n矩阵,则cij=max(aij,bij),其中i=1,2,…,m,j=1,2,…,n。

4) 直乘算子*:C=A*b,A和C分别为m×n、n×m矩阵,b为n维向量,则cji=aij·bj,其中i=1,2,…,m,j=1,2,…,n。

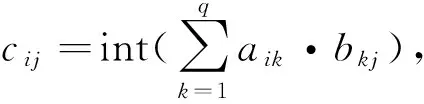

图2 CFFPN模型正反推理算法流程
2.1 正向推理
事件pi置信度公式如下:

(1)
若αk+1=αk,推理结束,否则继续由αk求得αk+1。
1) 变迁点火判别矢量。根据变迁点火规则,当变迁tj为预使能的,U(tj)为变迁预使能矢量值,公式如下:
(2)
若变迁达到点火条件,U(tj)=1,否则U(tj)=0。由上式可得变迁预使能点火序列为
U(t)=(U(t1),U(t2),…,U(tm))T
(3)
根据CFFPN点火规则,得到含有Token的库所变迁使能点火推导公式:
(4)
式(4)中:Mk-1-Mk-2表示第k-1次新点火标识矢量,Ik表示第k次点火的输入矩阵,Uk表示第k次点火的变迁序列。
2) 故障状态标识矢量推理。本文引用文献[8]的推导公式:
k= 1,2,3,…
(5)
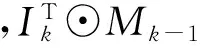
2.2 反向推理
CFFPN的逆向推理模型的输入、输出库所分别是CFFPN正向推理模型的输出、输入库所,即I-=O,O-=I。
在文献[9]的矩阵推理上进行改进,提出反向推理矩阵:
(6)
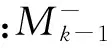
本文为了快速有效得检修故障源,引用最小割集的理论,其支路与结点的关联性质用n×m阶关联矩阵A表示,其中的元素aij定义如下:
(7)
式(7)中:i=1,2,…,n;j=1,2,…,m。
CFFPN模型中,使用已发故障关联矩阵来描述导致这一故障现象发生的Petri网拓扑结构,已发故障关联矩阵A*为


(8)
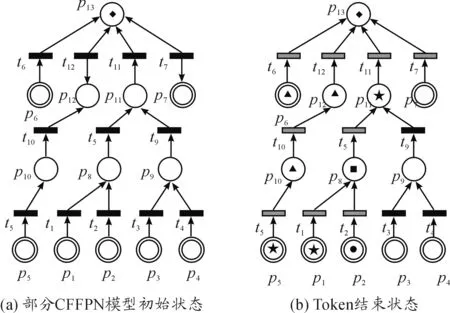
本文反向推理通过关联矩阵寻找任意故障现象的可能故障源,得到导致这一故障现象的k个最小割集G1,G2,…,Gk,k (9) 其中G={p1,p2,…,pi},i 本文以飞机气源系统为例说明CFFPN的应用,民机气源系统主要由APU引气分系统、发动机引气分系统、地面高压气源分系统和交输引气活门(CBV)等多个独立的子系统组成,通过飞机制造商提供的数据及手册信息,可以获得各个元器件及气源系统的故障模式、故障现象等故障信息。由于气源系统比较大,为了更好地进行诊断推理,本文选择APU引气子系统进行故障分析,其部分CFFPN模型如图3所示。库所集P={p1,p2,…,p13},其中,p1为APULCV开度偏小,p2为APULCV关位失效,p3为APU下游AMS引气管路焊缝破裂,p4为HPGCV开位失效,p5为APULCV开度偏大,p6为APU引气超温,p7为APU引气低温,p8为APUCKV卡在关位,p9为引气泄漏,p10为APUCKV卡在开位,p11为APU引气低压,p12为APU引气超压,p13为APU引气子系统故障。 本文初始值的确定主要根据专家知识库以及历史数据等,设定初值如下:库所初始置信度a0=(0.95,0.9,0.7,0.86.0.95,0.82,0.8,0,0,0,0,0,0)T;库所事件的权值Ω=(1,1,1,1,1,1,1,1,1,1,1,1,0)T;变迁阈值H=(0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5)T;变迁规则可信度U=diag(0.9,0.8,0.75,0.8,0.85,0.7,0.85,0.9,0.95,0.9,0.8,0.9);将α0、O、U、I代入式(1),推理得a3=a2=(0.95,0.9,0.7,0.86,0.95,0.82,0.8,0.855 0, 0.688 0, 0.807 5, 0.769 5, 0.726 8, 0.68)T,从而获得各库所事件的置信度,以此作为正反推理依据。 气源系统的APU引气系统工作时,未发生故障,但通过对测试槽进行检测时,预测有以下故障征兆,“APU引气超温”、“APULCV开度偏小”、“APULCV关位失效”和“HPGCV开位失效”。根据Token染色规则,在CFFPN模型中生成库所初始标志,如图3(a)所示,其系统初始状态标识向量M0=(0,1,0,1,1,1,0,0,0,0,0,0,0)T。按照2.1节的算法和公式对图3(a)模型计算推理得到U5=U4推理结束,模型库所最终标识向量为M4=(0,1,0,1,1,1,0,1,1,1,2,1,4)T,可知正向推理Token结束状态如图3(b)所示。从该模型中可以清晰看出p8、p9、p10、p11、p12、p13为故障征兆可能引发的故障。故障严重程度、引发路径及置信度等级如表2所示。工作人员可以根据故障预测信息,检查APU引气子系统相应部件,进而提高气源系统的可靠性。 图3 正向推理模型 表2 正向推理故障传播状态信息 图4 反向推理模型 对于CFFPN模型而言,考虑到符合实际系统的需求,尽量摆脱参数对于经验和专家知识的依赖,本文参照文献[12]的实例给出的学习和训练步骤对算法进行性能评估,使得CFFPN模型具有较强的自适应和泛化能力,推理结果更加准确无误。本文选取80个训练样本进行学习和训练,采用Matlab工具实现,将库所的实际输出与其期望值输出进行比较,结果如图5所示。由此可见,本文提出的模型输出值与期望值基本重合,表明该算法具有很好的适应性,保证故障推理的准确性。 图5 CFFPN参数期望值与实际值 本文提出了基于CFFPN模型故障诊断分析方法,建立了模拟气源系统故障的CFFPN仿真模型,预测气源系统在使用阶段的故障发生情况,给出了气源系统的故障发生严重程度及故障传播路径。该模型在模糊产生式规则基础上引入染色规则能够很好地表达故障传播特性,有效提高故障诊断效率。利用变迁点火矩阵进行正向推理,使工作人员能够对系统故障进行快速判断;结合最小割集理论进行逆向推理,在故障已经发生的情况下得到优先诊断次序,避免故障诊断的盲目性。另外,该方法具有一定的通用性,适用于民用飞机其他系统的故障诊断。 [1] 周虹,左洪福,苏艳,白芳.多工况过程动态SDG故障诊断[J].航空动力学报,2012(11):2539-2546. [2] TZACHI R,SOLOMON E S,Eugene S J.Reasoning with BKBs-algorithms and complexity [J].Annals of Mathematics and Artificial Intelligence,2004,40(3/4):403-425. [3] 祝加雄,贺元骅.基于并行禁忌神经网络和DS证据的飞机燃油系统故障诊断[J].计算机测量与控制,2014(6):1687-1689. [4] SU Y,LIU P.Multi-hierarchical Functional Directed Graph Modeling Method for Aircraft System Fault Diagnosis [J].Applied Mechanics and Materials,2014(541/542):1467-1472. [5] SU Y,ZHANG R.Test Strategy Optimization Method for Aircraft System Fault Diagnosis [J].WIT Transactions on Modelling and Simulation,2014(11):741-748. [6] 杨健维.基于模糊Petri网的电网故障诊断方法研究[D].成都:西南交通大学,2011. [7] 梁光夏.基于改进模糊故障Petri网的复杂机电系统故障状态评价与诊断技术研究[D].南京:南京理工大学,2014. [8] 程学珍,王程,于永进,伊利峰,陈强.一种基于模糊故障Petri网的三相异步电动机故障分析方法[J].电工技术学报,2015(17):132-139. [9] 马良荔,刘永葆,汪丽华.基于库所有色Petri网的故障诊断算法研究[J].计算机应用研究,2012(3):941-943,949. [10]曾庆锋,何正友,杨健维.基于有色Petri网的电力系统故障诊断模型研究[J].电力系统保护与控制,2010(14):5-11,127. [11]袁崇义.Petri 网应用[M].北京:科学出版社,2013. [12]李洋,乐晓波.基于模糊Petri网学习能力问题的最优化算法[J].计算机应用与软件,2010,27(11):127-130. [13]熊盛.模糊Petri网在某型武器载车系统故障诊断中的应用 [J].四川兵工学报,2014(4):84-87. (责任编辑唐定国) A Fault Diagnosis Analysis Method Based on Extended Color Fuzzy Fault Petri Net LING Yi-qin,SU Yan (College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China) Aiming at the uncertainty of traditional fault diagnosis method in analog fault propagation and diagnosis reasoning, a fault diagnosis analysis method based on extended color fuzzy fault Petri net (CFFPN) was proposed. Firstly, based on the traditional Petri net model, we introduced the the color rule of token, place and transition. The forward and backward reasoning were carried by further combining with the fuzzy generative rule and matrix operation, which enhanced the fault tolerance ability. The model of forward reasoning achieved intelligent evaluation of fault state with changing ignition discrimination matrix and reflected the fault propagation characteristics; The backward inference had preferred diagnosis by using the minimal cut sets theory methods and provided diagnostic order to avoid the blindness of the diagnosis. Finally, the pneumatic system was taken as a typical application object, which verified the effectiveness of the above methods. color fuzzy fault Petri net; color rule; minimal cut sets; fault diagnosis; pneumatic system 2016-07-11; 国家自然科学基金项目(U1233114) 凌益琴(1990—),女,硕士研究生,主要从事飞机系统故障诊断和智能系统开发研究。 10.11809/scbgxb2016.12.030 凌益琴,苏艳.一种扩展染色模糊故障Petri网的故障分析方法[J].兵器装备工程学报,2016(12):130-134. format:LING Yi-qin,SU Yan.A Fault Diagnosis Analysis Method Based on Extended Color Fuzzy Fault Petri Net[J].Journal of Ordnance Equipment Engineering,2016(12):130-134. V231 A 2096-2304(2016)12-0130-05 修回日期:2016-08-153 实例分析



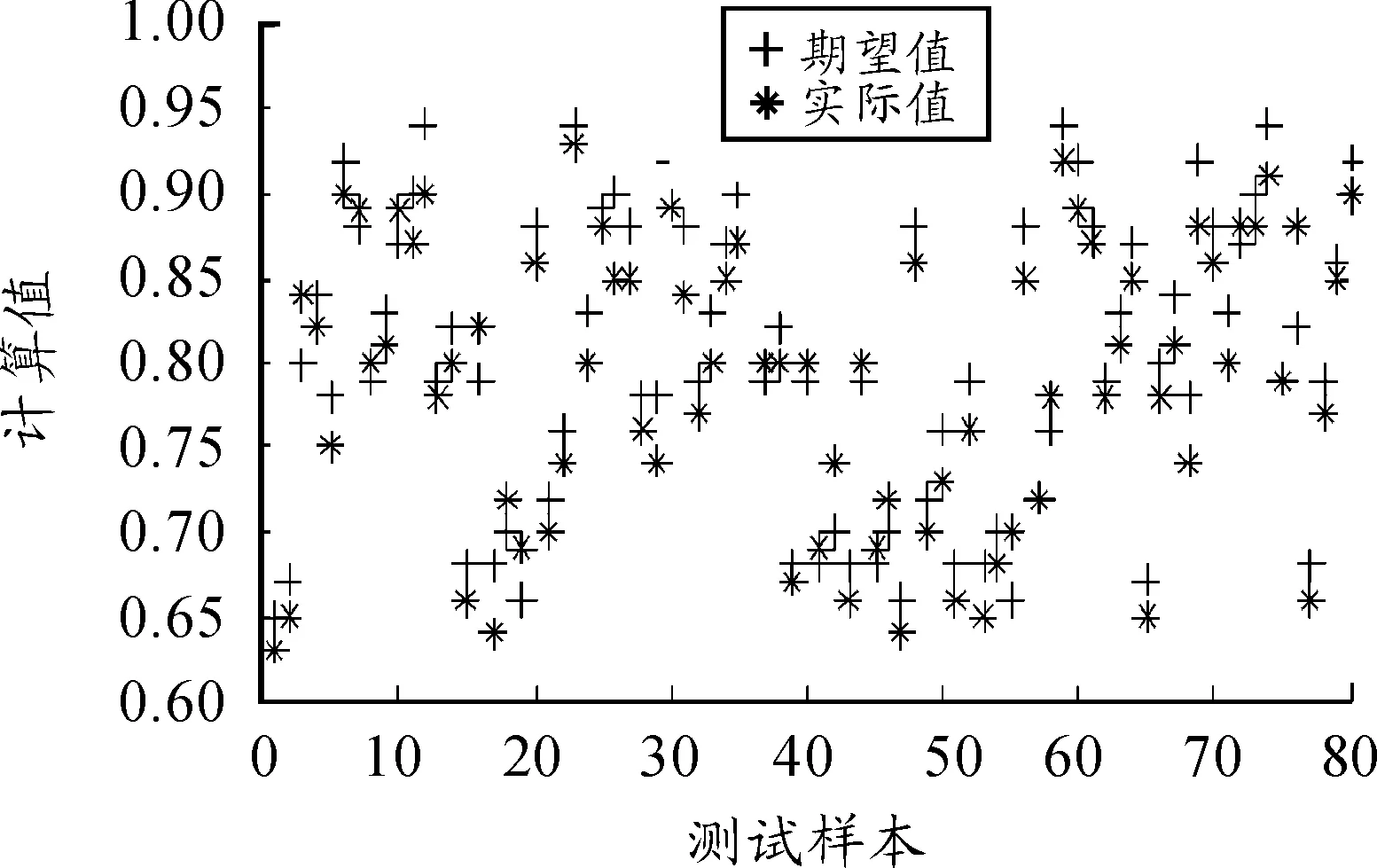
4 结论

