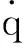基于滑模变结构的导弹制导律设计
陈昌旭,李 洋,祁 琪,孙 胜
(北京航天自动控制研究所,北京 100854)
【装备理论与装备技术】
基于滑模变结构的导弹制导律设计
陈昌旭,李 洋,祁 琪,孙 胜
(北京航天自动控制研究所,北京 100854)
为了实现导弹的精确打击,增强导弹的机动性,提出基于滑模变结构的导弹制导律。在设计趋近律时考虑到弹目距离的变化,使得系统状态轨迹快速且收敛到滑模面,并通过饱和函数替代符号函数抑制状态轨迹在达到滑模面时的抖动。仿真结果表明,滑模变结构方法相比于经典的比例导引方法,更能发挥导弹机动性并改善弹道,使导弹运动更加平滑。
非线性系统;滑模变结构控制;制导与控制
精确打击已成为现代战争的主要作战形式,是加速战争进程,决定战争胜负的关键要素。导弹的制导系统是导弹的大脑和中枢神经,它直接决定着制导性能和制导精度。制导律应对系统中存在的不确定因素具有一定的鲁棒性,为使系统性能达到某种指标下最优,常常采用非线性控制。变结构控制方法与常规控制方法的根本区别在于控制的不连续性,滑模变结构控制是变结构控制系统的一种最有价值的控制,它具有使系统结构随时间变化的开关特性,对于参数摄动和外部扰动具有很好的鲁棒性[1-2],因此得到了广泛的研究和应用,本文针对导弹末制导过程,设计了基于滑模变结构的制导律,并通过仿真验证了其在导弹制导系统中的高效性。
1 制导问题数学模型的建立
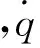
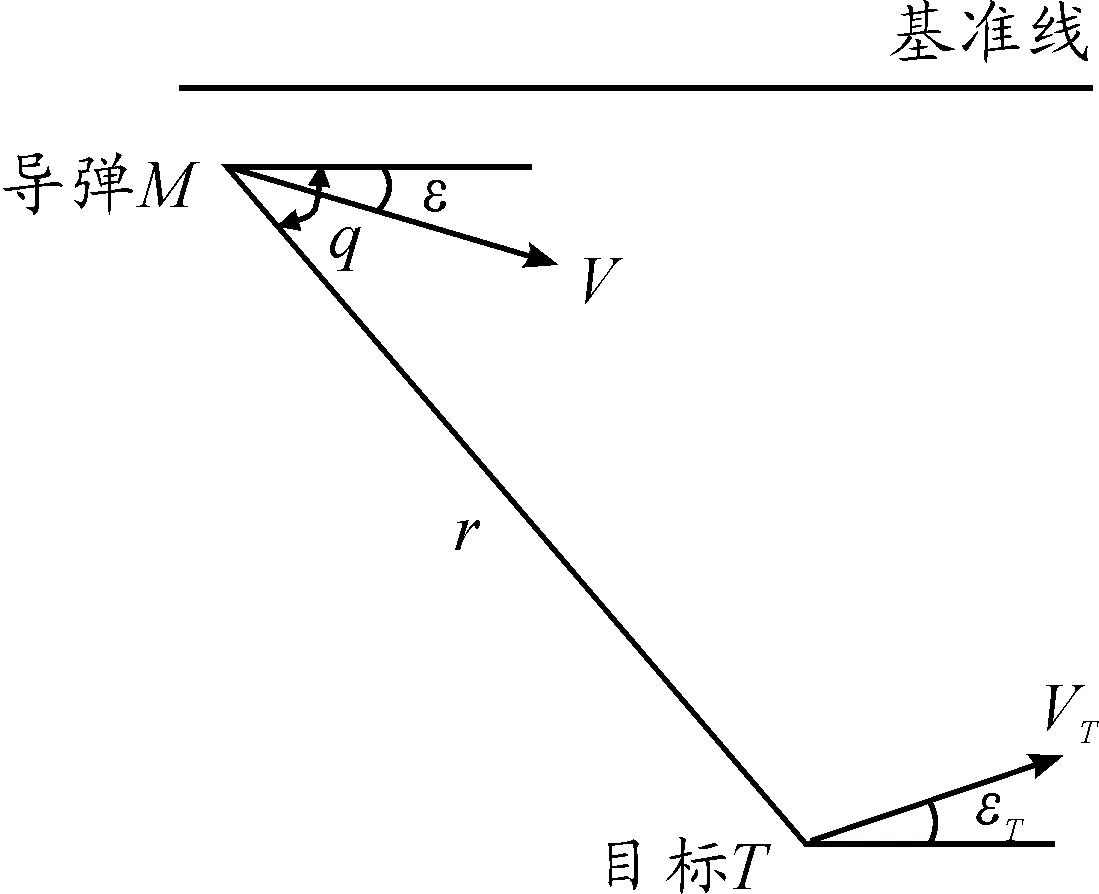
图1 导弹目标几何关系
(1)
弹体和目标的运动都与相对运动状态r和q非线性耦合在一起,不便于解析分析;与目标机动直接相关的目标加速度、与导弹控制直接相关的导弹加速度均未在模型中出现。考虑到实际制导过程中,沿视线方向不做控制,只需对导弹进行与视线垂直方向控制。将方程组的2式求对时间的一阶导数,可得:
(2)
做如下变换:
(3)
其中,ωq和uq分别为目标加速度和导弹加速度在视线法向上的分量。将式(3)代入式(2),得到视线角加速度:
(4)
(5)
根据状态方程,采用双通道过载控制方式,即对俯仰、偏航两个通道进行控制,滚动通道仅进行稳定控制,并在发射坐标系中设计制导律。由于发射坐标系中ox轴在过o点的水平面内,指向发射瞄准方向,oy轴垂直于过o点的水平面指向上方,oz轴与xoy平面相垂直并构成右手坐标系,在发射坐标系中进行纵侧向分离,分别对其进行制导律设计。
2 滑模变结构制导律设计
变结构控制系统,其控制器由若干个不同的连续子系统组成。各子系统的参数不同或结构不同,系统在工作过程中根据某种函数规则在这些子系统中切换。改善系统的动态性能,即使各子系统是线性的,整体系统也不是线性的,本质上是非线性系统。滑模变结构控制系统是结构随时间变化的不连续系统,此种开关控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动,即所谓的“滑动模态”或“滑模”运动。此种滑动模态是可以设计的,且与系统的参数及扰动无关。因此,处于滑模运动的系统具有很好的鲁棒性。
2.1 滑动模态趋近律设计
滑模变结构控制方法是通过控制作用,使系统的状态轨线运动到选取的适当切换流行,然后沿此流行渐近运动到平衡点。系统一旦进入设计好的滑动模态,在一定条件下对外界干扰及参数摄动具有不变性。根据准平行接近原理,希望在制导过程中趋于零,即导弹和目标之间保持恒定的视线角。因此,选取滑模面为
(6)
为了保证运动在趋近滑模面的过程中具有良好的品质,因此采用趋近律的概念和公式来保证正常运动品质,在指数趋近律[2]的基础上进行设计。
(7)
其中,ρ,k为设计参数,sgn(s)为符号函数,将式(7)微分方程求解,得:
各组大鼠给药42 d后,大鼠血清TGF-β1浓度依次为Nif+CsA组>CsA 组>Nif 组>对照组。与对照组相比,CsA 组、Nif+CsA组的血清TGF-β1水平均明显升高(P<0.05);Nif组虽略有升高,但差异无统计学意义(P>0.05)。与Nif 组相比,Nif+CsA组的血清TGF-β1水平明显升高(P<0.05),CsA 组虽略有升高,但差异无统计学意义(P>0.05)(表2)。
(8)
由式(7)可知,在滑模面s=0处的趋近速率为ρ,由式(8)可知,s>0时,当ρ>0、k>0、t>0、r>0时,在固定的时刻,增大k和ρ均能实现提高趋近速率。
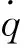
通过选取适当的参数保证系统在上述趋近律下能保证在期望的时间内到达滑模超平面,实现滑动模态。
将状态方程(5)代入趋近律式(7)可得导弹控制量:
(9)
对于式(9)得到的制导律,实际上就是导弹在栏截目标过程中制导平面的加速度指令。在实际应用中,目标的加速度ωq无法得到,因此常将其当作干扰项处理。整个制导律,类似于在传统的比例制导律中加入了变结构项。
进行纵侧向分离,分别求出纵向平面控制量uy和侧向平面控制量uz,得到的制导律如下:
(10)
2.2 抖振的抑制
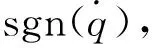

(11)
其中,d>0,它为小正数,表示边界层厚度。即存在一个小的区间,在此区间以外,饱和函数的形式与符号函数完全相同,而在区间(-d,d)内,用连续的函数把切换项连接起来。
上述方法实际上就是引入连续函数使系统变成连续系统。如果边界层厚度d选的足够小,仍可保持较高的鲁棒性。
2.3 可达性分析
引入饱和函数后的趋近律如下:
(12)
下面对可达性进行证明。
证明:根据Lyapunov第二法,取:
(13)
对式(13)求导并考虑状态方程(5)可得:
(14)
对于上式可做如下分析:



(5)当x2≡0时,视线角的变化率为零,即目标非机动运动,根据传统制导方法,能够完成制导。
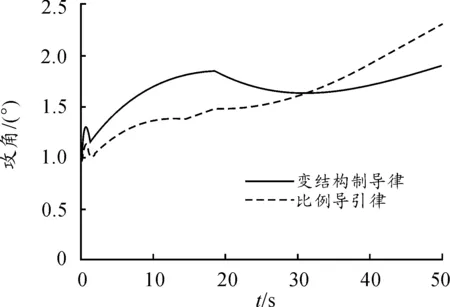
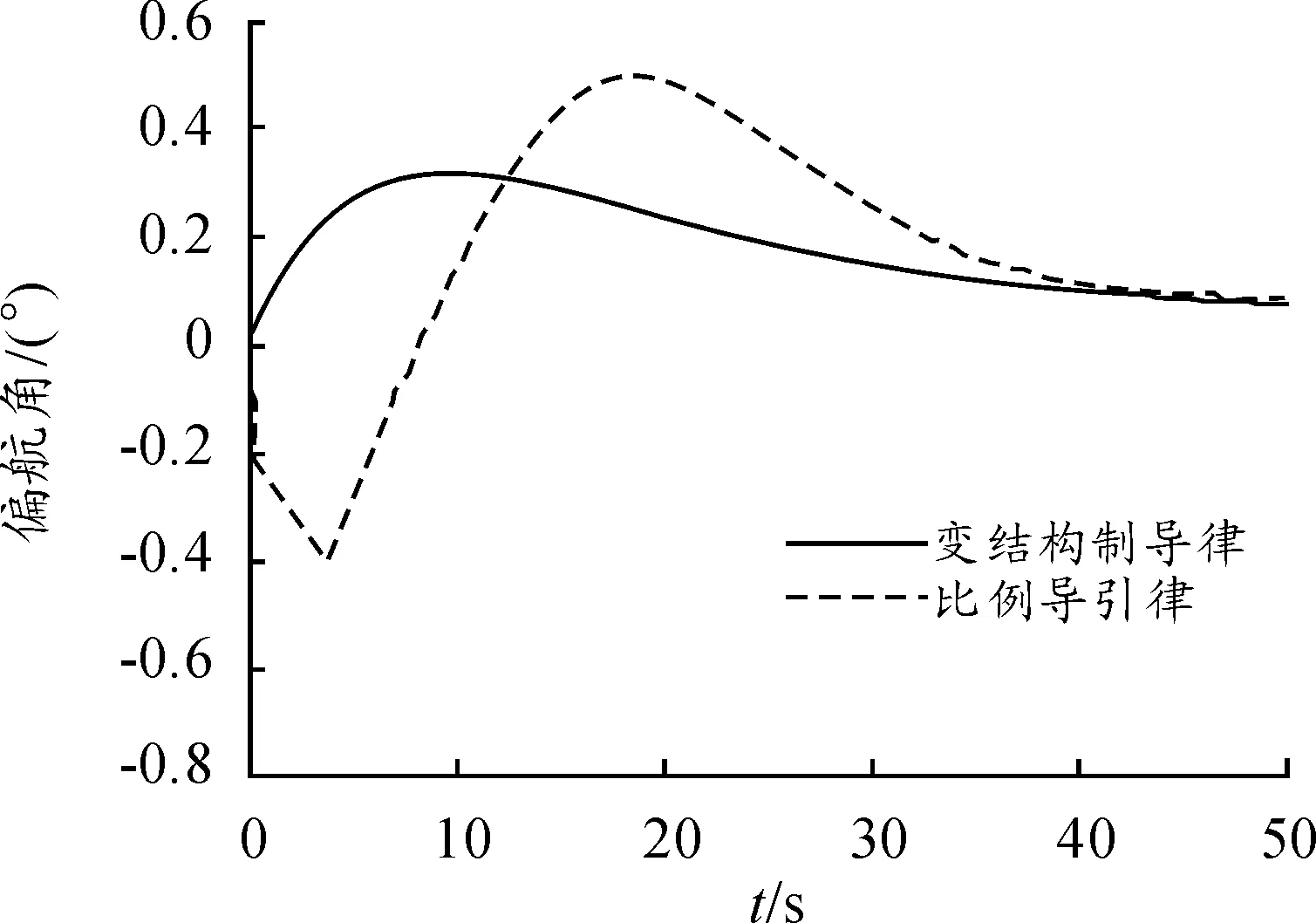
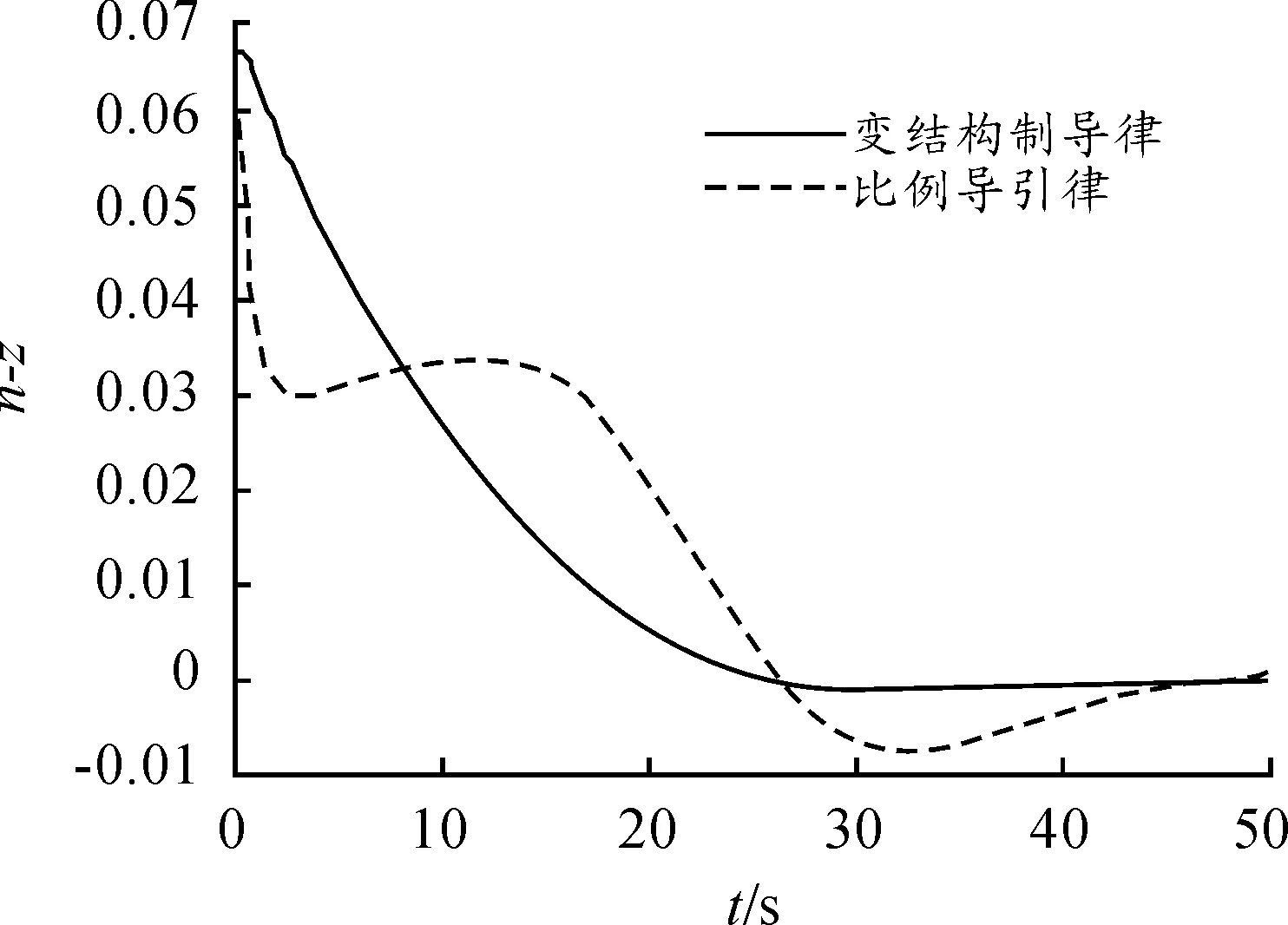
由于-d 为了进一步说明滑模变结构制导律的性能,采用比例系数K=3的经典广义比例导引制导律 (15) 进行对比仿真验证。导弹投放高度10 000 m,目标为海面匀速运动目标。仿真结果如下: 图2 导弹攻角 图3 导弹侧滑角 图4 导弹偏航角 图5 导弹横向过载 在控制回路参数基本不变的情况,经典比例导引和滑模变结构制导律随着时间增大,均可以使过载以及视线角趋于零,达到预期效果。就性能而言,变结构制导律的收敛速率明显快于经典比例导引法;经典比例导引法产生了较为强烈的弹体抖动,滑模变结构法能很好地抑制弹体姿态的抖动,弹体实际受到的过载更加平滑。 [1] GAO W B,WANG Y F,HOMAIFA A.Discrete-time variable structure control systems[J].IEEE Trans.on Ind.Electron,1995,42(2):117-122. [2] 高为炳.变结构控制理论基础[M].北京:中国科学技术出版,1990. [3] 孙胜,张华明,周荻.末端导引律综述[J].航天控制,2012,30(1):86-89. [4] 姚怀瑾,林德福,减路尧,王武刚.变结构经典比例导引制导性能对比研究[J].计算机仿真,2014,31(7):31-35. [5] 颜博.基于滑模变结构的防空导弹制导律研究[D].沈阳:东北大学.2011. [6] 尹永鑫.空地导弹滑模制导方法研究[J].飞行力学,2010,28(1):44-46. [7] 谢道成.带末端角度和速度约束的再入飞行器滑模变结构导引律[J].电光与控制,2014,21(11):46-50. [8] RAVINDRA K,BABU,SARMA I G,et al.Switched Bias Proportional Navigation for Homing Guidance Against Highly Maneuvering Targets[J].Journal of Guidance,Control and Dynamics,1994,17(6). [9] 曲萍萍,周荻.考虑自动驾驶仪动特性的终端角度约束滑模导引律[J].宇航学报,2013,34(1):2096-2105. [10]YANG Y N,WU J,ZHENG W.Variable Structure Attitude Control for an UAV with Parameter Uncertainty and External Disturbance[C].International Conference on Advanced in Control Engineering and Information Science. 2011:18-19. [11]谷志勇,沈明辉,韩彦东.最优滑膜变结构末制导律设计[J].弹箭与制导学报,2013,34(1):69-72. [12]王辚,高原,范文涛.基于反演变结构方法的变外形导弹控制系统[J].探测与控制学报,2014(3):46-51. (责任编辑周江川) Missile Guidance Law Design Based on Sliding Mode CHEN Chang-xu, LI Yang, QI Qi, SUN Sheng (Beijing Aerospace Automatic Control Institute, Beijing 100854, China) In order to achieve missile’s precision strike with more mobility. A guidance law design based on sliding mode was proposed. The reaching law considered change of distance between missile and target to insure state trajectory convergence to equilibrium rapidly, and to suppress the tremor state trajectory, alternative sign function by saturation function when reaching sliding surface. The simulation results show that compared to the classical method of proportional navigation law, the sliding mode can bring the flexibility and improve ballistic missiles, and make the missile movement smoother. nonlinear systems; sliding mode control; guidance and control 2016-09-15; 国家自然科学基金青年科学基金项目“高超声速飞行器攻击角度约束下有限时间收敛制导控制方法”(61403355) 陈昌旭(1991—),男,硕士研究生,助理工程师,主要从事导航制导与控制研究。 10.11809/scbgxb2016.12.014 陈昌旭,李洋,祁琪,等.基于滑模变结构的导弹制导律设计[J].兵器装备工程学报,2016(12):56-59. format:CHEN Chang-xu, LI Yang, QI Qi, et al.Missile Guidance Law Design Based on Sliding Mode [J].Journal of Ordnance Equipment Engineering,2016(12):56-59. TJ765.3 A 2096-2304(2016)12-0056-04 修回日期:2016-10-15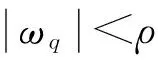
3 弹道仿真与结果分析
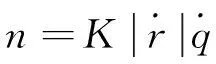

4 结论