改进的粒子群优化算法在物流配送中的应用
李 君,梁昔明,张 克
(北京建筑大学 理学院,北京 100044)
改进的粒子群优化算法在物流配送中的应用
李 君,梁昔明,张 克
(北京建筑大学 理学院,北京 100044)
选址问题的优化模型一般是多目标约束优化模型,综合考虑物流成本和物流服务能力,以物流成本最小化和物流服务能力最大化为目标,构建一个多目标优化选址模型,通过添加参数和运用约束处理方法,将选址问题化为单目标约束优化问题,并利用嵌入最速下降法的改进粒子群优化算法ZK_PSO_SD算法进行求解,所得数值分析和对比的结果表明,所建立的选址模型具有很好的实用性.
粒子群优化算法; 最速下降法; 物流服务能力; 成本最小化
随着全球经济的发展,以及信息技术的更新变革,物流行业得到了极大地发展,加之电子商务的推动,我国的物流业一直保持高速增长. 配送系统在物流系统中的地位重中之重,选择一个好的物流配送中心,对于整个物流配送系统至关重要. 在选择物流配送中心时,我们要选择一种优良的方案,使节俭花销、降低成本且保证质量的基础上服务水平最高. 近些年以来,选址优化问题已经成为科学研究的一个重要分支.
经典配送中心选址问题一般有以下3种类型:连续模型选址问题、离散模型选址问题和德尔菲专家咨询法选址方法[1]. 对于选点无约束、不考虑实际情况的选址问题,一般采用连续模型选址方法来求解,常见的几种连续模型选址方法是重心法、改进遗传算法、粒子群优化算法等. 离散模型选址问题[2]是备选的地点是有限的几个场地,而最佳的地址只能从这几个中选取,这类问题的求解主要借助库恩- 汉姆布里尔法、鲍摩- 瓦尔福法、反町氏法、整数或混合整数规划法等算法. 国内诸多学者也就相关问题进行了深入研究,取得了较大进展. 王战权[3]提出了采用遗传算法对混合整数规划模型进行分析求解,可以有效地提高算法的效率,提高选址问题的精确度. 刘海燕等[4]通过分析物流系统各要素间的逻辑关联,以物流配送中心选址作为对象构建了混合整数规划模型. 德尔菲专家咨询法选址的思路是将定性分析和定量计算相结合,将专家的判断以数值形式表现出来的方法.
随着研究的深入,针对经典配送中心选址问题的求解已经无法满足时代的发展. 除了经典配送中心选址问题以外,近年来国内外学者主要对带有距离限制的配送中心选址问题[5]、带容量限制的配送中心选址问题[6]、带道路容量限制的配送中心选址问题[7]等进行研究. 还有一些应急设施选址问题[8]、竞争设施选址问题[9]等也得到了很多专家和学者的关注. 上述的选址问题的情况比较复杂,因此需要对模型进行必要的简化,并且提出一些假设条件,才满足算法的需要. 因此,这些年专家和学者研究的重点主要在对各种经典问题的扩展研究上,即在考虑各种现实条件的前提下,提出的带有限制条件的路径优化问题,如最短时限运输问题[10]、带时间窗的路径优化问题[11]、带车容量限制的路径优化问题等. 虽然经典的物流配送选址问题相关的研究成果已经很丰富,但是与复杂多变的实际情况相比,这些研究还是不够,这就需要相关领域的学者和专家共同努力. 本文综合考虑物流成本和物流服务能力,以物流成本最小化和物流服务能力最大化为目标,构建一个多目标优化选址模型,通过添加参数和运用约束处理方法,将问题化为单目标约束选址优化问题来解决,利用嵌入最速下降法的改进的粒子群优化算法来进行求解,这样就为多目标选址优化模型的求解提供了一个新的思路.
1 嵌入最速下降法的基于增广Lagrange乘子法的改进粒子群优化算法
1.1 增广Lagrange乘子法
非线性约束优化问题的形式如下:
minf(x)x∈Rn
s.t.hi(x)=0,i=1,2,…,l
cj(x)≥0,j=1,2,…,m
l≤x≤u
(1)
增广Lagrange乘子法是一种较为常见的约束问题处理方法,其基本思想是在Lagrange乘子法中加一个能反映等式约束hi(x)和不等式约束cj(x)是否满足约束的惩罚项,在求解上述形式约束优化问题中,如果没有限制条件l≤x≤u,则将约束优化问题(1)就转化为了一系列如下无约束优化问题:
minP(x,λk,σk)
(2)
其中是P(x,λk,σk)代表的是在给定的λk和σk下,增广Lagrange乘子法第k步所求的无约束优化子问题. 而P(x,λ,σ)是增广Lagrange罚函数:
(3)
(4)
对于形如式(1)所示的约束优化问题,保留界约束条件l≤x≤u,在使用增广Lagrange乘子法的基础上得到如下形式的界约束优化问题:
minP(x,λk,σk)
s.t.l≤x≤u
(5)
其中P(x,λk,σk)表达式和式(2)中表述一致.
我们需要借助增广Lagrange乘子法的思想来求解式(1)的约束优化问题,然后将其化为一系列如式(5)所示的式子来求解. 求解过程分为两个步骤,并且是以内外两层结构的形式,在内层结构中主要是对问题(5)进行求解,得到一组最优解;外层迭代主要是修改λk和σk以及检查算法何时终止.
乘子向量λ和σ初始化时,为了方便计算,取λ0=(1,1,…,1),σ0=(10,10,…,10),在迭代过程中,Lagrange乘子向量λ的修正方法为:
(6)
(7)
σk+1=γσk
(8)
(9)

1.2 嵌入最速下降法的改进粒子群优化算法
在基本粒子群优化算法中,每个粒子j的位置和速度更新如下:
vj(t+1)=wvj(t)+c1r1(pj(t)-
xj(t))+c2r2(pg(t)-xj(t))
(10)
xj(t+1)=vj(t+1)+xj(t)
(11)
其中vj(t)为粒子j在第t代的速度,w表示惯性权重,是调整算法全局搜索能力和局部搜索能力的平衡因子,较大的惯性权重能增强算法的全局搜索能力,而较小的惯性权重则可以增强算法的局部搜索能力;c1为认知系数,c2为社会系数;r1,r2为服从均匀分布在区间(0,1)上的随机数,Pj为粒子j的个体历史最优位置,Pg为群体的历史最优位置. 最速下降法的最大特点就是沿着目标函数的负梯度方向获得下一个点,这样寻找的点必然比原来的点更加接近最优点. 因此可将最速下降法引入到基本粒子群优化算法中.
(12)
为搜索方向,根据:
xk+1=αdk+xk
(13)
(14)

1.3 改进粒子群优化算法的具体流程
(a) 初始化Lagrange乘子法中乘子向量λ0和罚参数向量σ0;
(b) 借助Lagrange函数,将约束优化问题(1)转化为界约束优化子问题(5);
(c) 初始化粒子群优化算法各参数,随机产生初始粒子及速度,并设定速度和位置的范围为[vmin,vmax],[Ld,Ud],令当前迭代次数t=0;


(f) 根据式(10)计算微粒下一代的速度vj(t+1),如果新计算出的速度值超出[vmin,vmax],则取边界值;
(g) 根据式(11)计算微粒下一代的位置xj(t+1),如果新计算出的位置值超出[Ld,Ud],则取边界值;

(j) 如果‖dk‖≤eps或k>4则转(o);否则,转(k);
(k) 令α=1;
(l) xk+1=xk+αdk;





(p) 根据式(6)~式(8)修正Lagrange乘子法参数λk和σk,转(b).
2 配送中心选址问题
配送中心选址和配送路径优化问题在物流配送关系链中起着至关重要的作用,一个合理的配送中心选址方案不仅要考虑成本的因素,而且要考虑客户的满意度水平,只有兼顾这两种因素,这样的配送中心才是我们需要的,才能满足现代物流配送中心的要求.
2.1 配送中心的成本组成及假设
优化计算离不开数学模型,但建模过程是极为复杂的,为了简化过程,需要做一些假设:
1) 每个需求点的需求量是已知的年需求量;
2) 不同单位的产品的运输费用一样;
3) 在配送过程中的速度是已知的,为一常数值,不考虑不同路段的差异问题;
4) 一个需求点仅由一个配送中心供应;
5) 运输费用与运量和距离成正比;
6) 系统总费用只考虑运输过程中的固定费用、运输费用以及流通配送中心产品的流通加工费用;
7) 配送中心没有囤货现象.
以方便建模和计算为目的,我们需要引用以下参数:
n: 需求点个数;
m: 配送中心备选地个数;
t: 拟建配送中心个数;
Dj: 第j个需求点的年需求量;
Fi: 在第i个候选作为配送中心的每年固定花销;
Ci: 每件物品在第i个配送中心的存放花销;
xij: 配送中心i为需求点j供应的货物量;
hij: 从配送中心i到需求点j供应的单位运费(包括装卸、运输花销);
物流配送中心的选址成本优化模型如下所示:
(15)
2.2 物流配送中心服务能力模型
物流配送中点的服务水平和能力与很多因素有关,为了使其得到提升,首要的任务是定性到定量因素的转变. 一般的处理方法是用时间来量度,并且考虑货物的受损程度等因素. 一般用“时间满意度函数”来表示顾客对产品或者服务的时间满意度与顾客等待时长的对应关系. 接下来分析连续条件下的线性的“时间满意度函数”. 如图1所示.
设Tij是需求点i接受配送中心j等候的最短时长,Li为需求点i的顾客评价级别达到“非常满意”时最长等待货物时间,Ui是需求点i的顾客评价级别为“非常不满意”时等候的最短时长,其中Li≤Ui;Tij为需求点i的顾客对配送中心j的反应时间的满意度水平.
(16)
则配送中心系统的时间满意度可以按照以下计算:
(17)
2.3 配送中心选址模型
本文研究的配送中心选址问题是一个多目标优化问题,目标是在保障高服务水平的同时力求运输成本最小. 该问题将路面信息抽象为方形的区域,每个地点的信息都是一个二维的点,坐标信息即表示其具体位置,本文问题的研究是在给定顾客需求量和具体位置的基础上展开的.
配送中心连续性选址的物流成本模型可表示为:
(18)
配送中心选址问题的目标函数是在二维空间中选取一个或多个点作为配送中心,在保障高服务水平的同时力求运输成本最小. 配送中心选址的多目标优化模型如下:
(19)
其中,F1,F2均为目标函数,分别代表运输成本和配送中心系统的服务能力. 模型中的符号说明如下:(xi,yi)表示用户i的位置信息;(Xj,Yj)表示j的位置信息;Dij表示j到i的距离;H表示单位运费率;M表示需求点顾客数;N表示j的个数;Wi表示i的物品需求量;(xQ0,yQ0)、(xQ1,yQ1)分别代表方形配送区域的起始点、终止点坐标.
3 举例分析
本文采取的思路就是将多目标约束优化问题转变为单目标约束优化问题,就可以得到形如式(1)的约束优化问题,其形式如下:
(20)
其中0<α<1,K1,K2分别代表F1和F2的最大值. 这样处理的目的是让F1和F2处在对等的位置上,因为F1的数值相对于F2比较大,因此需要引进K1,K2来平衡两个数的大小. 如此就得到一个单目标约束优化问题式(20),针对式(20)的求解,可利用ZK_PSO_SD算法来求解. 现给定物流配送区域,范围是(0,0)到(100,100). 40个需求点[12]在此区域内随机分布,如图2所示. 要求在上述区域的需求点中找到四个地址作为配送中心j,分别标记为P1,P2,P3,P4. 已知运费率H和需求点的需求量均为一个单位. 所有配送中心运输派件的速度是50,需求点i的Li=2,Ui=3. 约定算法中终止迭代次数为200,种群数量为30,取K1=1 000,K2=160.
因此该物流配送中心选址的多目标优化模型如下:
(21)
接下来采取的措施就是将如式(21)所示的有两个目标函数的有约束问题转变为只有单个目标函数的约束优化问题,对于不同的α值,会有不同的结果. 公司根据自己的实际情况确定α值,若公司较看中成本,则选取较小的α值;否则,反之. 就本章而言,选择α=0.7. 这就将多目标约束优化问题转变为单目标约束优化问题,就可以得到形如式(1)的约束优化问题,其形式如下:
(22)
针对式(22)的求解,可以借助嵌入最速下降法的改进粒子群优化算法的ZK_PSO_SD算法,利用MATLAB2014b实验平台,借助ZK_PSO_SD算法对问题(22)进行30次独立试验得到的配送中心的位置坐标为P1(73.62,64.8)、P2(21.54,33.87)、P3(44.39,62.04)、P4(47.59,0.54),如图3所示.
在同等条件下,Nash均衡求解算法[13]得到的4个优化物流配送中心的地址,它们分别是P1(73.74,65.2),P2(21.23,34.92),P3(44.61,61.72),P4(47.64,0.00). 如图4所示.
Nash算法和ZK_PSO_SD算法的改进结果如下表1所示,通过Nash算法和ZK_PSO_SD算法结果对比,可以看到在服务水平差距不大的情况下,ZK_PSO_SD算法相比于Nash算法可以更好地降低运输成本,因此,ZK_PSO_SD算法在选址问题上的运用是有效果的,是一种实用的算法.
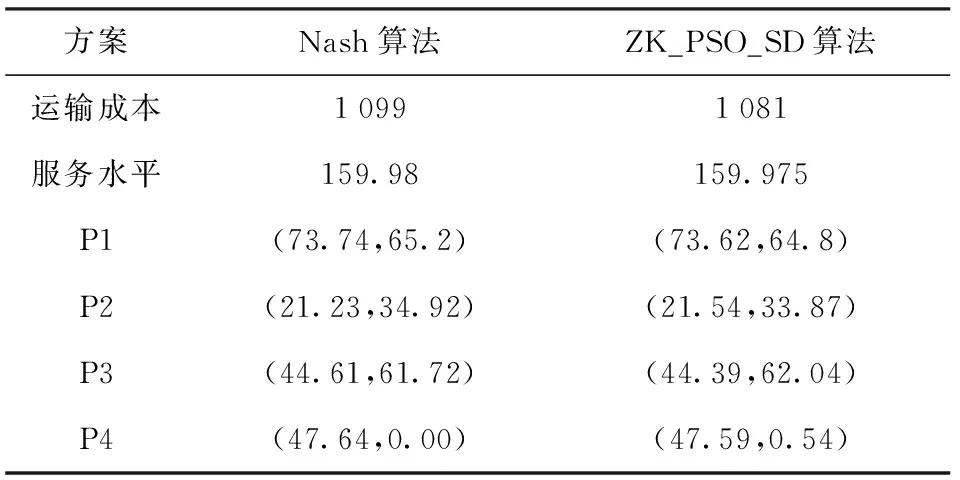
表1 Nash算法与ZK_PSO_SD优化算法计算结果对比
接下来可以思考,能否得到需求点对应的配送中心?一般来说,一个需求点对应一个配送中心,可以参考其中的一个量度作为衡量的标准得到每个需求点对应的配送中心. 如选择利用距离的大小作为衡量的标准,可以很清晰地得到每个需求点对应的配送中心. 如表2所示,X值对应的是每一个需求点的横坐标,Y值对应的是每一个需求点的纵坐标. 例如(1,0)而言,它到配送中心P1的距离为97.683 916 79,到配送中心P2的距离为40.356 651 25,到配送中心P3的距离为75.572 418 91,到配送中心P4的距离为46.64,故而可得需求点(1,0)到配送中心P2的距离最短,因而由配送中心P2向需求点(1,0)运货. 每一个需求点对应的配送中心均可得到,表2中已标出,这样就达到了我们处理问题的目的.
4 结论
通过介绍多目标优化模型,然后简单的描述了选址问题的背景、物流成本模型和物流配送中心服务能力模型. 将连续的有约束条件的具有多个目标函数的选址问题转变为只有单个目标函数的连续约束优化问题,之后再使用基于增广拉格朗日乘子法的改进粒子群优化算法ZK_PSO_SD算法,对一个不仅要考虑成本的因素,而且要考虑客户的满意度水平的配送中心选址方案进行试验. 在给定α值的前提下,相比于Nash优化算法,在客户满意度水平相差不多的情况下,ZK_PSO_SD算法选取的配送中心的物流成本最低,这就说明ZK_PSO_SD算法在处理选址问题上是行之有效的.
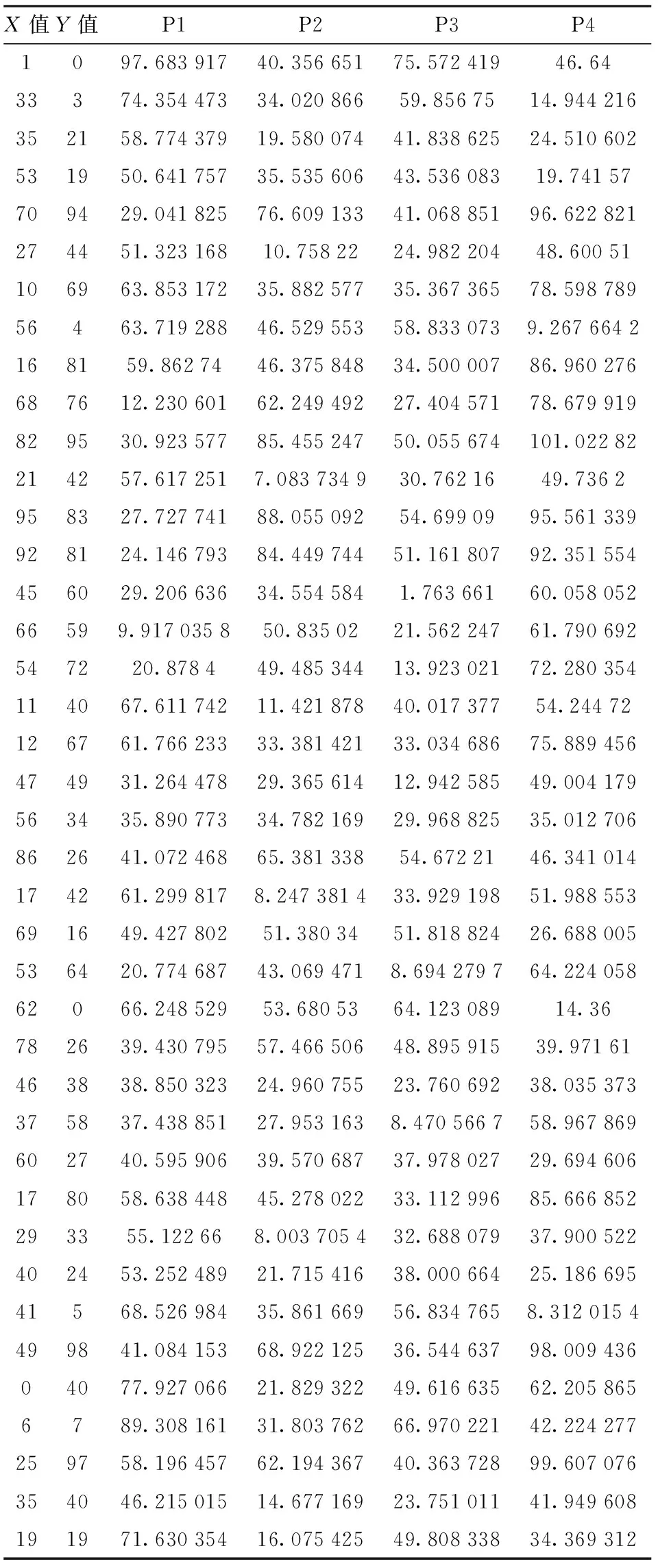
表2 需求点与配送中心对应关系图
[1] 蔡林宁.物流系统规划——及实例分析[M].北京:机械工业出版社,2008:1-58, 182-229
[2] 王非,徐渝,李毅学.离散设施选址问题研究综述[J].运筹与管理,2006(10):64-69
[3] 王占权,杨东援.配送中心选址的遗传算法研究[J].实用物流技术,2001(3):11-14
[4] 刘海燕,李宗平,叶怀珍.物流配送中心选址模型[J].西南交通大学学报,2000,35(3):311-314
[5] 赵斌,王媛,李珍萍.带距离限制的双配送中心选址模型[J].物流技术,2011,30(1):69-71
[6] 鲁晓雪,李珍萍.带容量限制的多配送中心选址问题[J].物流技术,2011,30(1):67-70
[7] 李珍萍,李婷婷,梁志新.带道路容量限制的多配送中心选址问题的数学模型与算法[J].统计与决策,2013,378:37-40
[8] Jaramillo J H, Bhadury J, Batta R. On the use of genetic algorithems to solve location problems[J]. Location Analysis,2002,29(6):761-779
[9] 杨丰梅,华国伟,黎建强.一个竞争选址问题的新模型及其算法[J].系统工程理论与实践,2006(7):18-24
[10] 李珍萍.最短时限运输问题及解法[J].中国管理科学,2001,9(1):50-56
[11] 马华伟,左春荣,杨善林.多时间窗车辆调度问题的建模与求解[J].系统工程学报,2009(5):607-613
[12] 龚延成.物流配送点选址模型及其算法研究[J].中国公路学报,2003,16(2):123-126
[13] 李艳,谢能刚,王付宇,等.物流配送中心多目标优化选址的仿真设计[J].计算机仿真,2012,29(7):234-237
[责任编辑:佟启巾]
Appliction of Improved Particle Swarm Optimization Algorithm in Logistics Distribution
Li Jun, Liang Ximing, Zhang Ke
(School of Science, Beijing University of Civil Engineering and Architecture, Beijing 100044)
Location problem of the optimization model is generally a multi-objective constrained optimization model, which is considered of the goal that has the logistics cost minimization and logistics service capability maximization, and then building a multi-objective optimal location model. By adding parameters and using the constraint handling method, the location problem is changed into a single objective constrained optimization problem, and the improved particle optimization algorithm based on the steepest method is used to solve the problem of ZK-PSO-SD algorithm. The results of numerical analysis and comparison show that the established location model has good practicability.
particle swarm optimization (PSO); steepest descent method; logistics service capability; cost minimization
2016-07-09
国家自然科学基金项目(61463009); 北京市自然科学基金项目(4122022); 中央支持地方科研创新团队(PXM2013_014210_000173)
李 君(1989—), 男, 硕士研究生, 研究方向: 最优化智能算法及其应用.
1004-6011(2016)04-0058-07
TP301.6
A

