基于零空间追踪和SWT的柴油机信号降噪研究

吴春志， 贾继德， 张玲玲， 贾翔宇， 张帅

(1. 军事交通学院军用车辆系， 天津 300161； 2. 96274部队， 河南 洛阳 471002)

·测试与诊断·

基于零空间追踪和SWT的柴油机信号降噪研究

吴春志1， 贾继德1， 张玲玲2， 贾翔宇1， 张帅1

(1. 军事交通学院军用车辆系， 天津 300161； 2. 96274部队， 河南 洛阳 471002)

为减少柴油机振动信号的噪声干扰，提取有用的信息，提出了一种基于零空间追踪算法和同步压缩小波变换相结合的组合降噪方法，利用压缩小波对主频信号精细重构的优点与零空间追踪算法的自适应分解的特点对信号进行降噪处理。该方法相比EMD更加适应柴油机振动信号特点，仿真和实例信号表明，该方法取得了较好的降噪效果。

零空间追踪； 信号处理； 压缩小波

柴油机机械结构复杂，激励源较多而且运行条件十分恶劣，从缸体采集振动信号进行故障分析时会有较强的噪声干扰，严重制约了对故障信号的处理及对故障类型的判断。为了有效提取故障信息，提高故障特征分析的准确性，研究人员提出了很多种降噪的方法。传统的小波分析因其良好的时频特性以及多分辨率的特点，在信号降噪方面得到较为广泛的应用[1-3]，但是处理信号时需要选取相应的小波基，小波基对降噪效果有较大影响[4]，这限制了小波分析在降噪方面的应用。Huang提出的经验模态分解(EMD)方法能够自适应地分解信号，不再受小波基选取的困扰，受小波分解阈值降噪的启发，研究人员利用EMD自适应地进行阈值降噪,取得了一定的成果[5-7]，但是EMD缺乏理论支持，而且对于具有调幅调频以及冲击信号的柴油机振动信号来说，EMD的降噪效果不是很明显。零空间追踪算法(null space pursuit，NSP)也是一种自适应分解算法，对于此类信号分解降噪效果要好于EMD[8]。

同步压缩小波变换(SWT)是由Daubechie提出的一种时频重排方法，该算法以小波变换为基础，是小波变换的进一步发展。通过对小波变换的复数谱沿着频率轴方向进行重排，可显著提高时频分辨率，而且对信号重构不失真[9]。该方法已经在信号分析、特征提取等方面取得良好的应用效果[10-12]。

为了进一步提高零空间追踪算法的分解降噪能力，本研究提出一种组合降噪方法。利用同步压缩小波对信号的主要分量进行精细重构，再用NSP对每个分量信号进行分解，去除残余分量后合成，达到降噪的目的。

1 零空间追踪算法

1.1 算法介绍

零空间追踪算法是由Silong Peng提出的一种新的基于算子的信号分解算法。区别于经验模态分解算法(EMD)，EMD得到本征模态函数(IMF)根据的是信号原始的局部极值，而零空间追踪算法利用局部奇异线性算子分解信号的过程是一个最优化问题的正则化方法，主要目的在于将信号分解为一系列局部窄带信号以及一个残余分量。对于含噪信号来说，噪声部分集中在残余分量中，因此NSP也可以对信号进行降噪处理。

1.1.1 局部奇异线性算子

局部奇异线性算子是零空间非零且具有紧支特性的一种线性算子[13]。该算子作用于信号时会去掉属于局部奇异线性算子零空间的部分，从而实现对信号的过滤，通过运算，信号会被分为属于和不属于算子零空间的两部分，有利于时域的局部化。

1.1.2 局部窄带信号

窄带信号可以描述为A(t)=cos(ωt+φ(t))，其中A(t)为调制幅值的带限信号，最大频率远小于ω，φ(t)为相位函数。如果某一信号在时间轴任意处存在一个邻域，且该邻域内的信号可被近似看成是窄带信号，那么这个信号称为局部窄带信号[14]。

1.1.3 算法过程

基于算子的分解算法主要是对式(1)求解，

S(t)=S1(t)+U(t)。

(1)

式中：S(t)为原信号；S1(t)为第一级或第二级局部窄带信号；U(t)为残余分量。

由于S1(t)是局部窄带信号，所以存在一个局部奇异线性算子T，使得T(S1)(t)=0。零空间追踪算法优化解出U(t)，

(2)

1.2 与EMD方法的对比

NSP和EMD都可以对非平稳信号进行自适应分解，EMD的分量IMF按照频率由高到低排列，而NSP分解出的窄带信号按照能量排列，而且NSP在对调幅调频的机械冲击信号分解方面优于EMD。用两种方法对同一个仿真信号进行分析对比验证。

1.2.1 建立仿真信号

仿真信号是在文献[15]的基础上进行了一些修改。

(3)

(4)

X=X1+X2。

(5)

式中：时间t=mod(kT,1/fm)；指数频率α1=300 Hz，α2=400 Hz；信号X1的调制频率fm1=100 Hz，载波频率f1=2 000 Hz；信号X2的调制频率fm2=100 Hz，载波频率f2=4 000 Hz。仿真信号的时域及频域见图1。

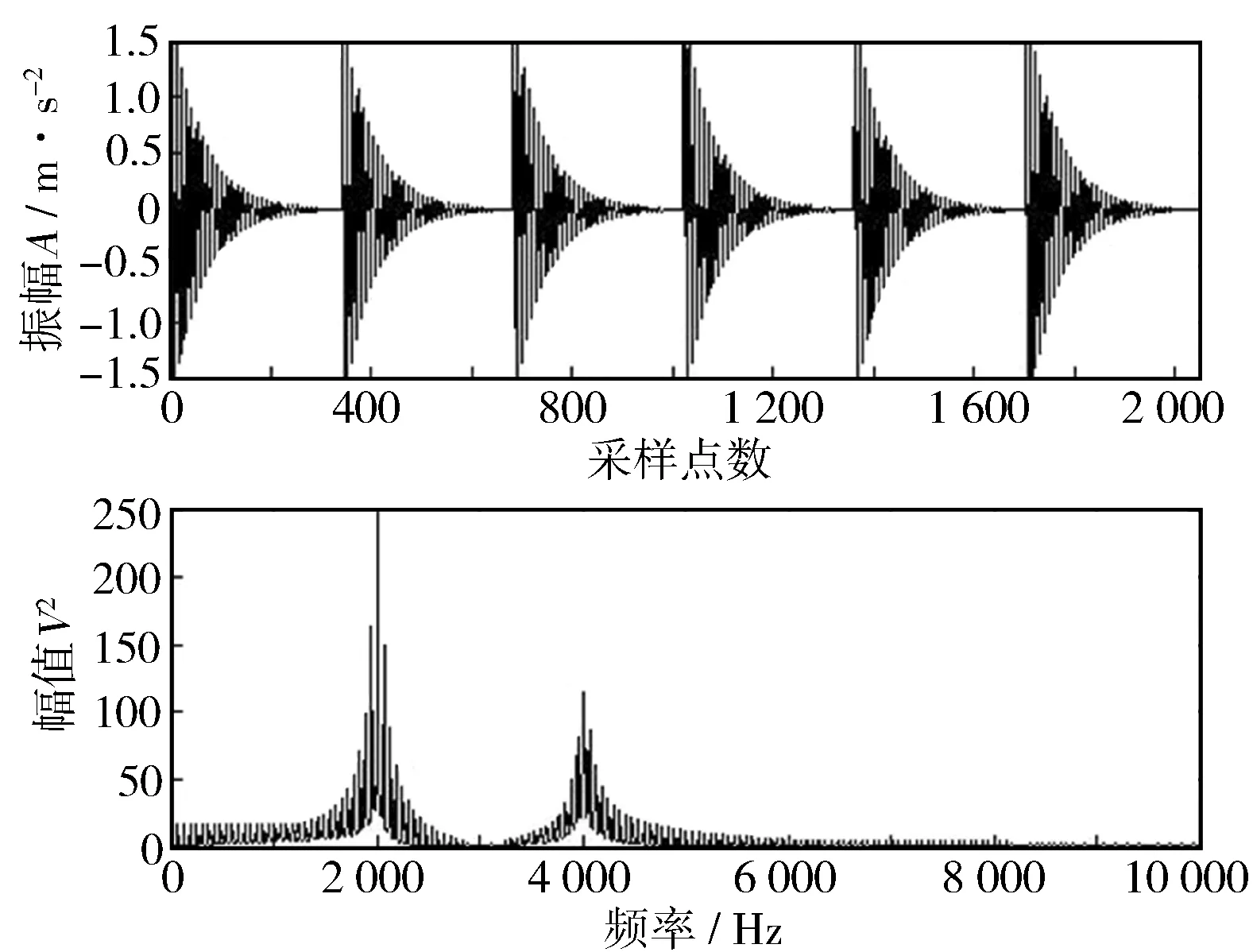
图1 仿真信号时域及频域图

1.2.2 对比分析

分别用NSP和EMD算法对信号进行分解，由于前4个分量能量占比达到了95%以上，所以对前4个分量进行分析对比。如图2所示，NSP算法的前2个分量便将X1和X2解调出来，而EMD的几个IMF分量没有将调频的冲击信号解调出来。因此对于带有调频、冲击信号的往复机械信号，NSP解调效果更好。

2 同步压缩小波变换

2.1 算法介绍

压缩小波算法以小波变换为基础，时频域有很高的分辨率。

(6)

(7)

(8)

SWT是一种时频重排算法，但是与以往的重排算法不同，SWT在提高时频分辨率的同时，还可以针对时频图中的特征段信号进行重构，可表述为

(9)

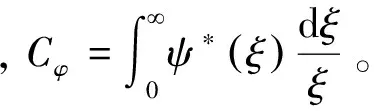
2.2 信号重构

对仿真信号进行压缩小波变换得到时频图(见图3)，从图中可以看到，两段特征区域对应信号的两个分量，利用压缩小波对其精细重构可以得到分量信号。

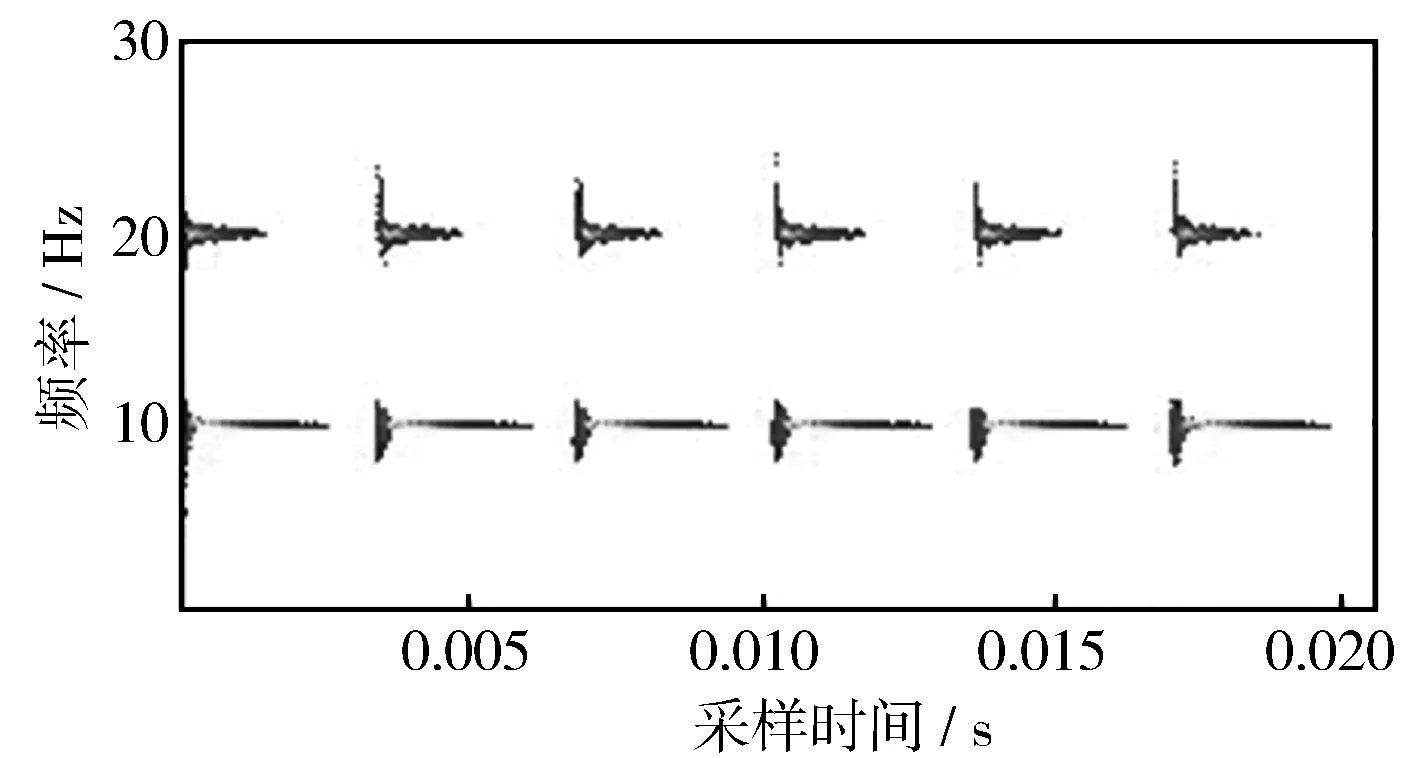
图3 仿真信号时频图

3 组合降噪分析

零空间追踪算法处理含噪信号时，剔除残余分量即可达到一定的降噪效果，通过上述分析可知，解调效果优于EMD算法。运用同步压缩小波对信号主分量区域进行重构，再利用零空间追踪算法对重构信号进行消噪处理，经仿真信号验证，降噪效果要好于仅使用NSP算法。图4示出NSP结合SWT信号处理方法的流程。

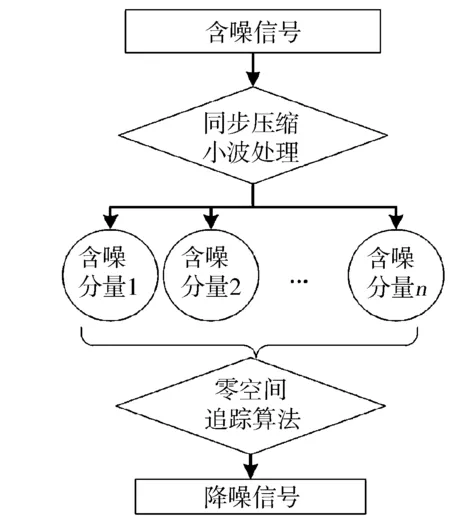
图4 NSP结合SWT信号处理流程

对仿真信号x依次加入随机噪声，得到不同信噪比的含噪信号xn, 分别用小波包、Morlet小波、EMD和SWT&NSP组合方法对含噪信号进行降噪处理。图5示出信噪比为10 dB的含噪信号降噪后的时域图，可以发现，组合降噪方法的降噪效果明显好于其他方法。图6示出采用4种降噪方法降噪后的信号和原信号的均方误差(MSE)值，MSE越低，信号的还原度越高。由图可知，组合降噪的方法要优于其他降噪方法，且随着信噪比降低，该方法有着较强的鲁棒性。

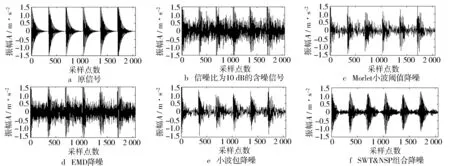
图5 原信号及各方法降噪后时域图

图6 不同信噪比下4种降噪方法对比

4 应用实例

4.1 信号采集

试验测取东风EQ2012汽车柴油发动机的曲轴振动信号，将振动加速度传感器放置在油底壳与缸体结合部，正对第四道主轴承左侧(面向发动机前进方向，测点见图7)，测取振动信号。采样频率20 000 Hz，取采样点数4 096点。

图7 振动传感器布置

4.2 信号解调与降噪

图8示出发动机实测的振动信号时域曲线及频谱，可见信号中有较强的噪声干扰。利用组合降噪的方法对实测信号进行处理，得到去噪后的时域及频域信号(见图9)。从图中可以看出该方法降噪效果明显，而且能解调出信号能量集中的主要分量(见图10)。

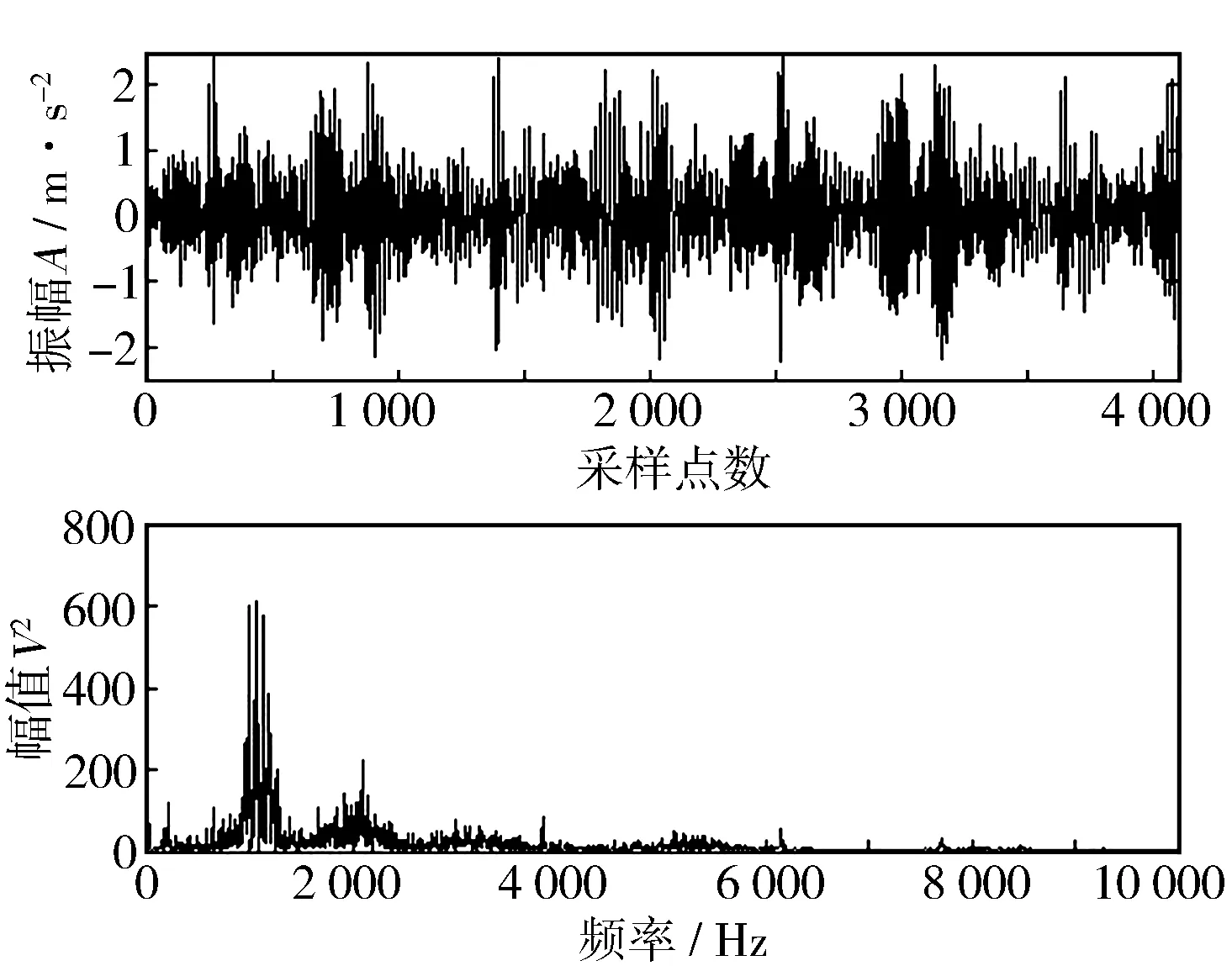
图8 柴油机信号及频谱

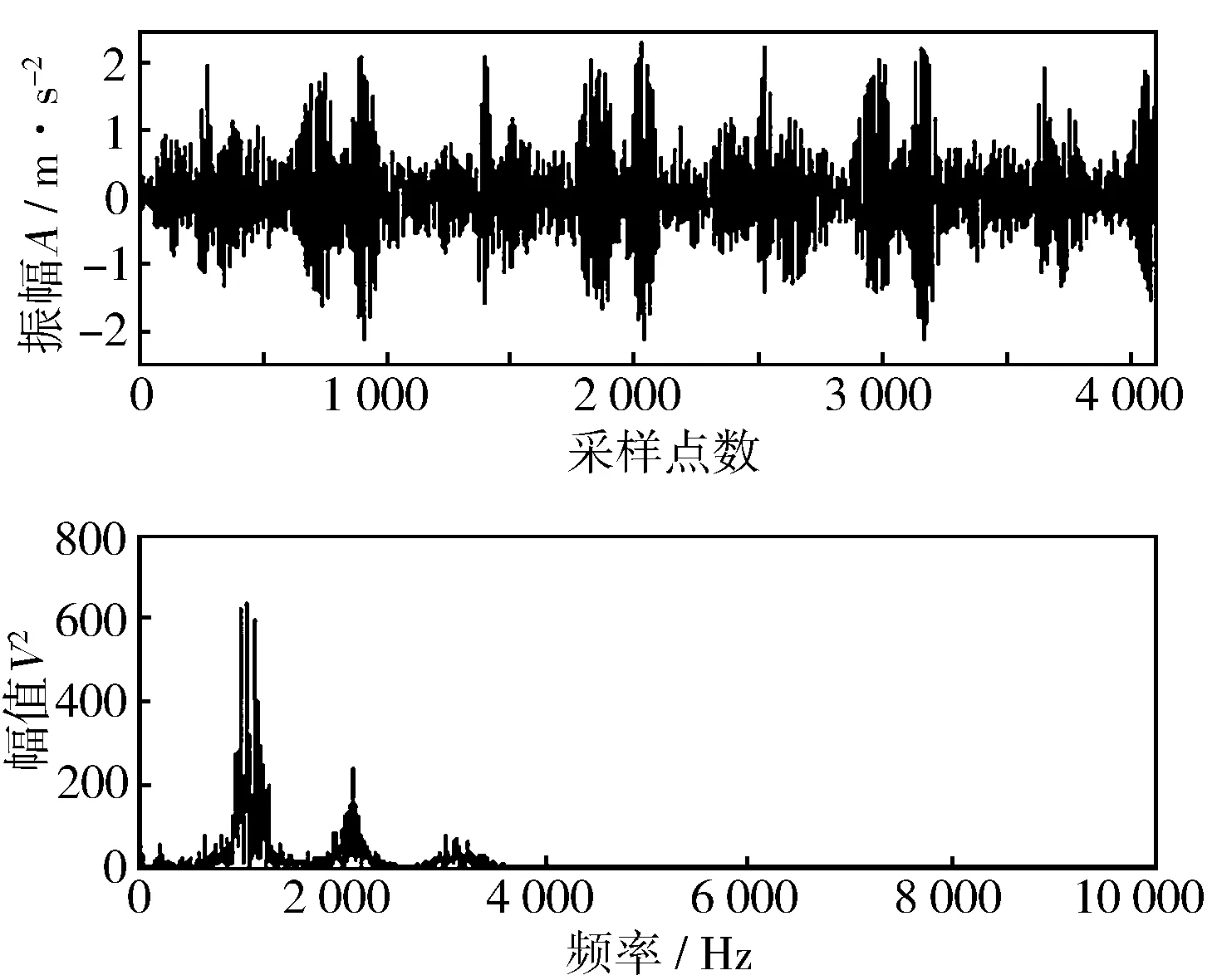
图9 组合降噪后信号及频谱

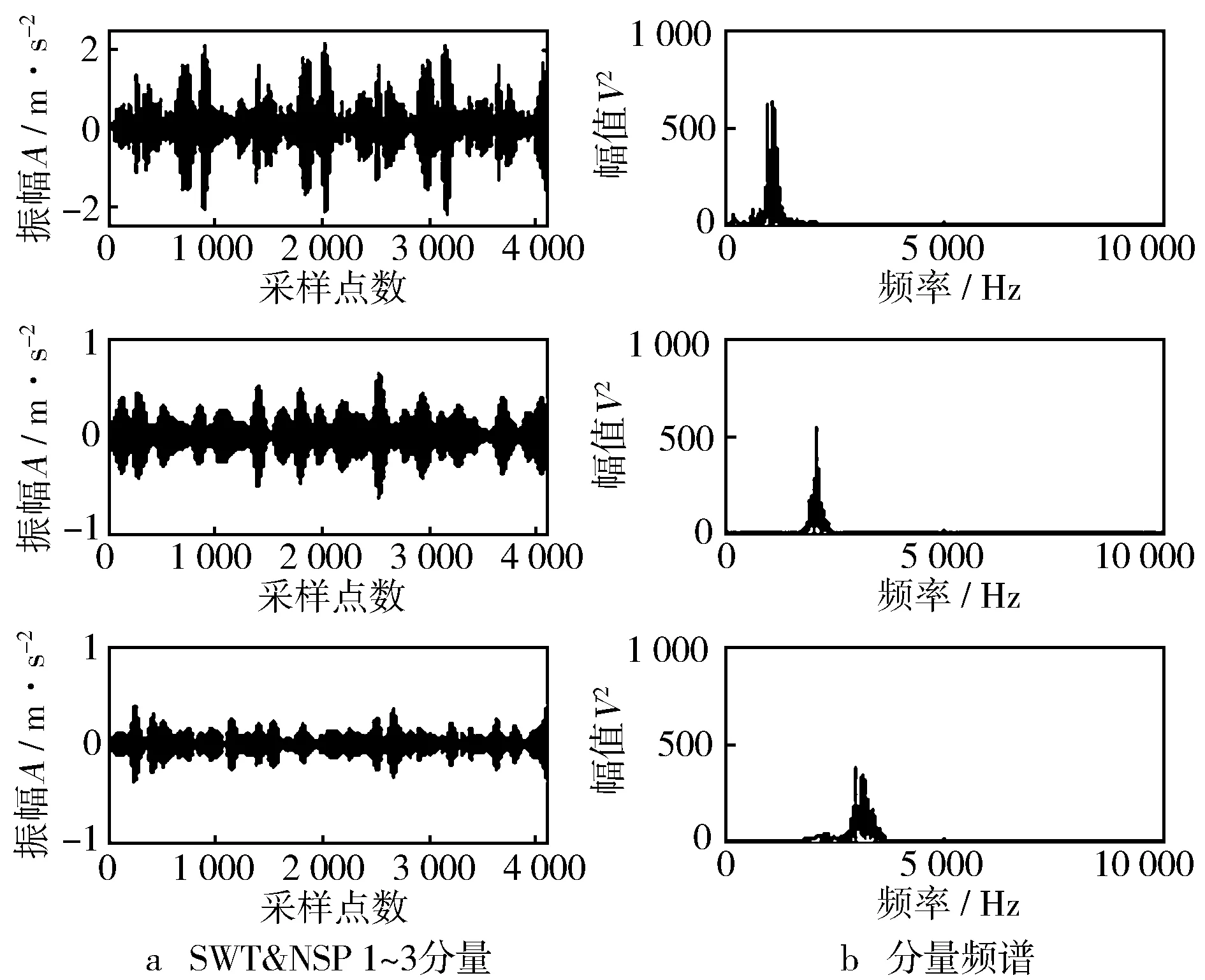
图10 解调的主要分量及频谱

5 结束语

根据柴油发动机振动信号特点提出了一种由零空间追踪算法和同步压缩小波相结合的组合解调与降噪的方法，通过仿真以及实例信号进行分析验证。NSP算法对于调幅调频的机械冲击信号的解调效果优于EMD，同步压缩小波变换可以根据时频图像对信号进行区域重构，利用二者算法的特点进行组合处理柴油发动机振动信号，取得了较好的降噪与解调的效果。

[1] Pizurica A,Philips W.Estimating the probability of the presence of a signal of interest in multiresolution single and multiband image denoising[J]．IEEE Transaction on Image Processing,2006,15(3):654-665.

[2] Portilla J,Strela V，Wainwright M J,et al.Image denoising using scale mixtures of gaussians in the wavelet domain[J]．IEEE Transaction on Image Processing,2003,12(11):1338-1351.

[3] Atoniadis A，Bigot J．Wavelet estimators in nonparametric regression：a comparative simulation study[J]．Journal of Statistical Software，2001，6(6)：1-83．

[4] Lei Zhang,Bao P,Xiaolin Wu， et al.Multiscale LM-MSE-based image denoising with optimal wavelet selection[J].IEEE Transactions on Circuits and Systems for Video Technology,2005,15(4):469-481.

[5] Mao Y，Que P．Noise suppression and flaw detection of ultrasonic signals via empirical mode decomposition[J]．Russian Journal of Nondestructive Testing，2007，43(3)：196-203．

[6] 邹清，汤井田，唐艳．Hilbert-Huang变换应用于心电信号消噪[J]．中国医学物理学杂志，2007，24(4)：309-312．

[7] Kopsinis Y，McLaughlin S．Empirical mode decomposition based softthresholding[C]//Proceedings of the 16th European Signal Processing Conference.[S.l.]：EURASIP，2008．

[8] 肖维维,栾卫军,彭思龙，等.基于三阶线性微分算子的零空间追踪算法[J].系统工程理论与实践,2013,33(5):1283-1288.DOI:10.3969/j.issn.1000-6788.2013.05.025.

[9] Daubechies I,Lu J,Wu H T.Synchrosqueezed wavelet transforms: An empirical mode decomposetion-like tool[J].Applied and Computational Harmonic Analysis，2011,30(2):243-261.

[10] Eugene Brevdo,Neven S Fuckar,Gaurav Thakur,et al.The Synchrosqueezing algorithm: a robust analysis tool for signals with time-varying spectrum[J].Signal Processing,2011,93(5):1079-1094.

[11] Songtao Xi,Hongrui Cao,Xuefeng Chen,et al.A Frequency-Shift Synchrosqueezing Method for Instantaneous Speed Estimation of Rotating Machinery[J].Journal of Manufacturing Science and Engineering,2015,137:031012-11.

[12] Zuo-Cai Wang,Wei-Xin Ren ,Jing-Liang Liu,et al.A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J].Journal of Sound and Vibration，2013，332：6016-6028.

[13] Peng S,Hwang W L.Adaptive Signal Decomposition Based on Local Narrow Band Signals[J].IEEE Transactions on Signal Processing,2008,56(7):2669-2676.

[14] Silong Peng，Wen Hang Hwang．Null Space Pursuit：An Operator-based Approach to Adaptive Signal Separation[J].IEEE Transactions on Signal Processing，2010,58(5):2475-2483.

[15] Sheen Y T．A complex filter for vibration signal demodulation in bearing defect diagnosis[J]．Journal of Sound and Vibration，2004，276(1)：105-119．

[16] Daubechies I,Maes S.A nonlinear squeezing of the continuous wavelet transform based onauditory nerve models[J].Wavelets in Medicine and Biology,1996:527-546.

[编辑： 潘丽丽]

Denoising of Diesel Engine Signal Based on Null Space Pursuit and Synchrosqueezed Wavelet Transform

WU Chunzhi1, JIA Jide1, ZHANG Lingling2, JIA Xiangyu1, ZHANG Shuai1

(1. Department of Automobile Engineering, College of Military Transportation, Tianjin 300161, China;2. Unit 96274 of PLA, Luoyang 471002, China)

In order to reduce the noise of diesel engine signal and extract the useful information, a method consisted of null space pursuit (NSP) and synchrosqueezed wavelet transform (SWT) was proposed. The denoising of signal was conducted according to the characteristics of SWT accurate reconstruction of signal main frequency and NSP adaptive decomposition. Compared with EMD method, the proposed method was more suitable for the vibration signal of diesel engine. The simulation and testing results show that the method has a good denoising effect.

null space pursuit; signal processing; synchrosqueezed wavelet transform

2016-04-23；

2016-07-07

后勤保障部重点项目(BS311C011)

吴春志(1991—)，男，硕士，主要研究方向为信号分析、特征提取及故障诊断；523649763@qq.com。

贾继德(1962—)，男，教授，博士，主要研究方向为信号分析、特征提取及故障诊断；jide@ustc.edu。

10.3969/j.issn.1001-2222.2016.06.015

TH212； TH213.3

B

1001-2222(2016)06-0078-05