基于小波检测信号间断点的应用分析

张祥字+岳亚军

【摘要】 局域变换及分辨率高的特性是小波变换具有的很显著应用很广泛的特征，文中针对信号突变检测的基本原理和方法做了详细的探讨。通过研究小波在信号处理中的应用，提出了小波变换检测信号间断点的技术。通过信号的多尺度分析，相对有效的检测出故障信号的起始位置，从而解决傅里叶变换不能解决的一些问题，对故障信号的诊断提供了有益的方法。

【关键字】 小波变换 突变检测 多尺度

一、引言

小波分析已经在20世纪90年代进入了全面应用阶段，小波分析的自适应性和数学显微镜性质使其在各个领域方方面面中都得到了广泛的应用，尤其是在信号处理、图形图像处理、故障检测、特征提取等方面。小波变换是一种新的时频分析方法，同时具有表征信号时域和频域局部信息的能力，可依据信号的具体形态动态调整时间窗和频率窗，在低频部分用较低的时间分辨率提高频率分辨率，在高频部分用较低的频率分辨率对时间进行精准定为。正是因为这些特征，使得小波分析可以探测信号的瞬态并展示相应的频率成分，从而克服了傅里叶变换在单分辨率上的缺陷。文中针对间断信号讨论了信号突变点的检测方法。

二、连续小波变换

2.1连续小波变换的定义

小波变换中“小”表明基函数为有限的区域；“波”表明基函数是震荡的；其他窗函数都有母小波推导出。变换的概念与短时傅里叶变换一样，但不是得出信号的频率参数，而是尺度参数，即频率的倒数。

式中和是和的傅里叶变换。

对（2）式分析，频域上小波变换的傅里叶变换是频谱与小波函数共轭的乘积，则可以发现：如果是幅频相对集中的带通函数，小波变换具有表征待分析信号局部特征的能力；a越大，小波的区域限越大，在频域上小波基的宽度越大。采用不同尺度的a处理时，Ψ（aΩ）的中心频率和带宽不同，但“中心频率/带宽”是个常数。

三、信号的突变检测

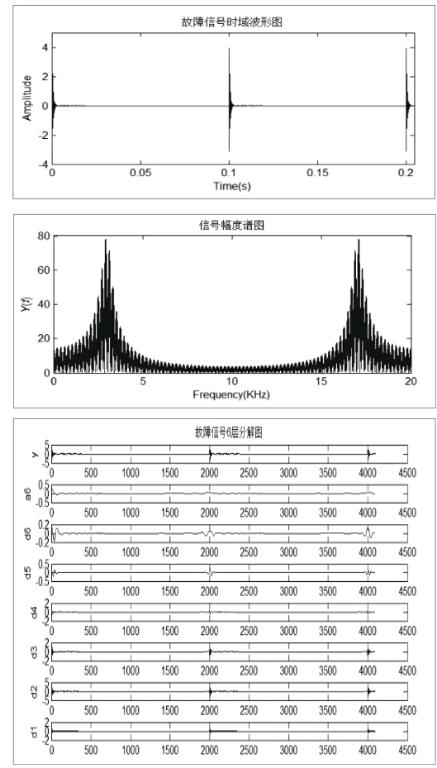
定义1 设n是非负整数n

|f（x|0+h）-Pn（h）|≤A|h|α

则说f（x）在x0处为Lipschitz a。如果上式对所有x0∈（a，b）均成立，且x0+h∈（a，b），称f（x）在（a，b）上是一致Lipschitz a。Lipschitz a指数越大，函数越平滑；函数在一点连续可导，Lipschitz a指数为1。在一点导数有界可导但不连续Lipschitz a指数也为1。若f（x）在x0处Lipschitz a<1，函数此时在该点是奇异的。若在x0处有界但不连续的函数，该点的Lipschitz a指数为0。若检测信号的突变点，必须选择正则小波。

通过对一故障信号的分析，可以发现故障信号在傅里叶变换下的频谱图中并不能准确的发现突变点的位置，此表明了傅里叶变换不具有时间分辨的能力。故障信号经小波变换进行6层分解图中，高频部分的第二层、第三层尤为清晰的反映出信号发生突变的断点位置，可以看到断点部分包含的高频分量在小波分析中具有很明显的呈现能力。从中也可以发现信号的有用信息主要在小波系数上得以呈现，小波变换更能刻画信号的细节对信号区分故障检测有很好的能力。同时值得注意的是，为了避免小波变换中的交叠干扰，在进行处理分析时，多尺度综合起来进行观察会有更精准的检测结果。

四、结论

小波变换对信号的突变检测因其具有的奇异性和多分辨率性使其具有很精准的定位功能。利用多尺度小波变换的方法，能有效的检测出突变位置，对一些系统的实时故障检测提供了有利的探索方法，有着极其广泛深远的应用前景。

参 考 文 献

[1]汤红诚，著信.小波变换在故障诊断中应用.仪器仪表学报，2003，24（zl）

[2]张常年，赵红怡.基于小波变换的故障信号分析与检测.红外与激光工程，2002年4月，第31卷第2期

[3]丁玉美，阔永红，高新波.数字信号处理—时域离散随机信号处理.西安：西安电子科技大学出版社.1997年

[4]胡昌华，张军波，夏军，张伟著.基于matlab的系统分析与设计—小波分析.西安：西安电子科技大学出版社.1999年

[5]刘贵忠，邱双亮.小波分析及其应用[M].西安：西安电子科技大学出版社.1992年