等温条件下可压缩理想气体的伯努利方程

俞锦涛 陶宗明

(1解放军陆军军官学院学员三旅，安徽 合肥 230031；2解放军陆军军官学院基础部物理教研室，安徽 合肥 230031)



等温条件下可压缩理想气体的伯努利方程

俞锦涛1陶宗明2

(1解放军陆军军官学院学员三旅，安徽 合肥 230031；2解放军陆军军官学院基础部物理教研室，安徽 合肥 230031)

不可压缩流体的伯努利方程在解释飞机机翼升力时出现了矛盾.从这个矛盾出发，本文建立理想气体的等温过程模型，运用能量守恒推导出了等温条件下可压缩理想气体的伯努利方程.通过比较分析可知:不可压缩理想气体的伯努利方程在等温条件下形式上可变成等温可压缩理想气体的伯努利方程,但本质上是有区别的；与等熵条件下的伯努利方程比较，两者成立条件不同,方程的形式也不一样;等温条件与等焓条件在本质上是一致的, 伯努利方程形式和本质都不变.

伯努利方程；理想气体；等温条件；可压缩条件

一般大学基础物理教材中的伯努利方程是在不可压缩条件下推导出来的，它描述了流体沿着一条稳定、非粘滞、不可压缩的流线移动行为，该方程是流体力学的一个重要规律.对于液体而言，不可压缩的条件很容易满足，但是对于气体而言，不可压缩的条件就有点苛刻了.

图1是分子之间作用力与距离的关系[1]，液体的分子间距在r0(r0为平衡距离)附近，气体的分子间距一般在10r0以内，根据图1可以看出当分子间距小于r0时，斥力急剧增大，因而液体不易被压缩；而气体的分子间距约在r0～10r0之间，相互作用力表现为吸力，因而易被压缩.在运用不可压缩流体的伯努利方程解释与气体相关的一些问题时，可能就遇到了一些矛盾.图2是飞机机翼升力的示意图，一般的解释是机翼的升力来自于上下两部分的压强不同，由不可压缩流体的伯努利方程可知，上方流速大压强小，下方流速小压强大，由压强差产生了升力.但由理想气体压强公式p=nkT可知,若大气温度相同，机翼上下方的压强不同只能是由气体分子数密度n不同引起的.气体分子数密度不同，也就是气体密度不同，这就与不可压缩的条件矛盾！也就是说，用不可压缩条件下伯努利方程，得出了结果气体是可压缩的？李复教授提出了在等熵条件下可压缩流体的伯努利方程[2]，等熵条件是指流体和外界没有热量交换，这一过程进行比较快，气体来不及与外界交换能量.低速可压缩条件下气体的伯努利方程形式如何呢？等温条件下可压缩理想气体的伯努利方程，它适用于低速情况，本文对这一方程进行了推导，并对该方程进行了分析和讨论.

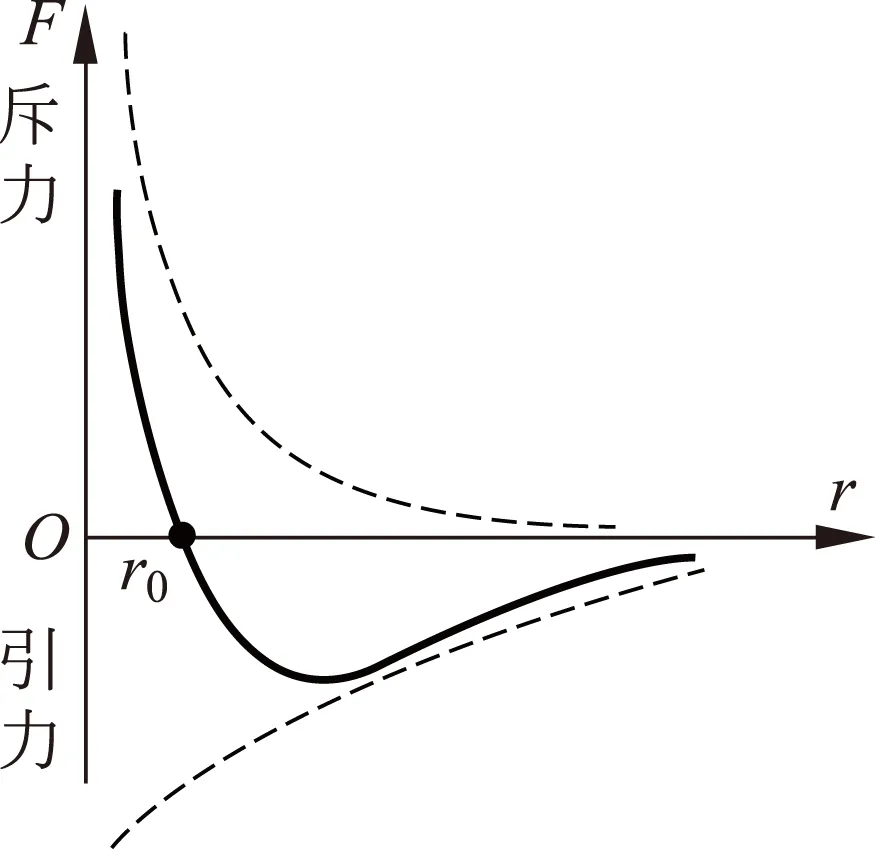
图1 分子之间的作用力与距离关系

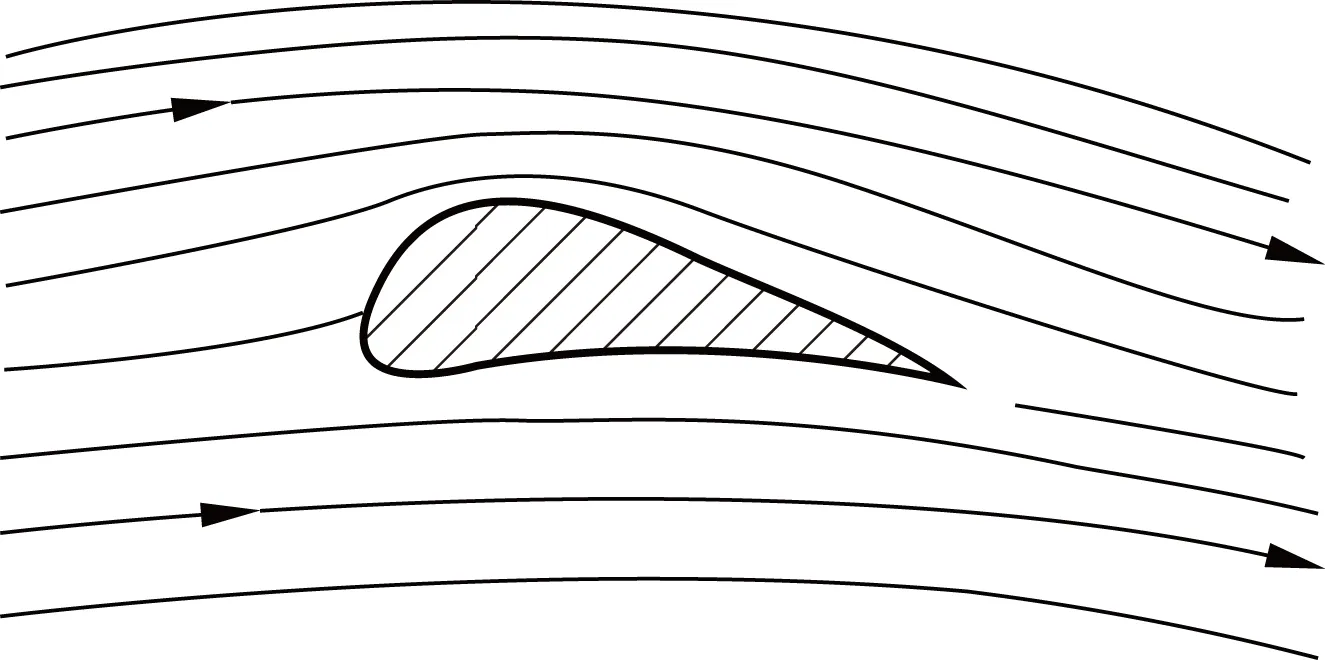
图2 飞机机翼升力原理示意图

1 理论推导

等温过程是实际过程的一个很好近似，在这一过程当中，理想气体的内能保持不变.

可压缩的理想气体，是指不考虑气体内部的粘滞力的可压缩气体. 图3是可压缩理想气体的示意图，气体沿着一横截面变化的流管流动，且流管各处的高度不同.流管内气体是稳流体，气体在空间上不均匀，但在时间上均匀即不随时间变化而变化，就是说对于流管的某处点Ai，压强为pi、密度为ρi，当经过任意Δt时间后，Ai处密度和压强不变.

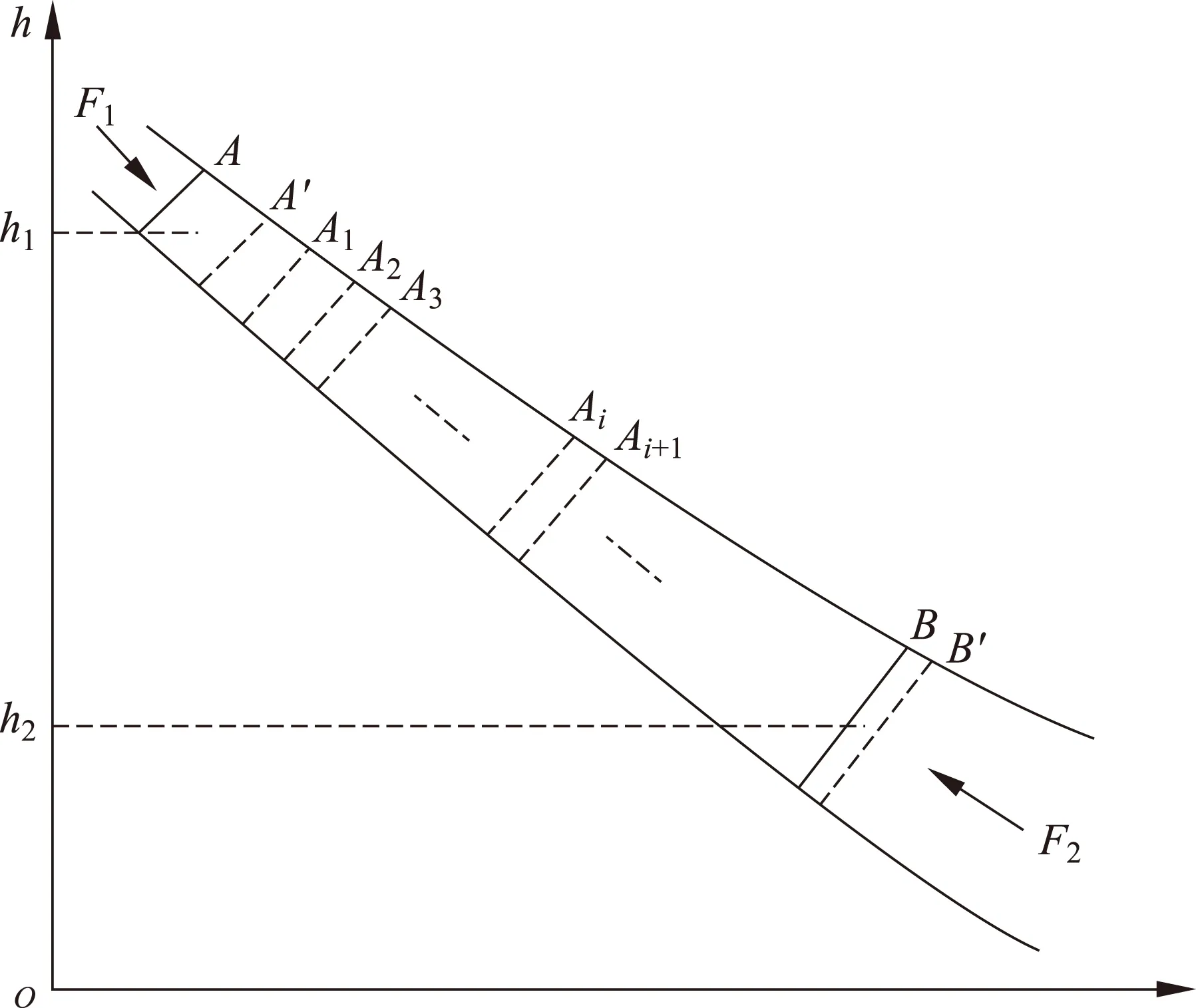
图3 可压缩理想气体的示意图

把图3中A到B之间的理想气体作为一个系统，将A、B之间的气体分割成质量相等的N等份，每一份的质量设为Δm.再设经过Δt的时间后，系统移动到A′、B′ 处(图中虚线表示)，且A、A′之间的质量为Δm.由于考虑的系统是稳流体，则A′、B之间的气体状态不变，系统的移动过程可以认为是A、A′之间的质量为Δm的气体直接转移到了B、B′处.在图3中，A、A′之间的体积元的高度是h1,压强为p1,气体所受的力F1，同样的在B、B′之间的体积元分别为h2、p2、F2.设A、A′之间密度为ρ1和B、B′之间密度为ρ2，并且(A、A′)、(B、B′)两微元气体体积分别为ΔV1和ΔV2，内能分别为E1、E2.那么两个外力对系统做的功ΔW为

ΔW=p1ΔV1-p2ΔV2

系统机械能和内能的增量为

由能量守恒可得

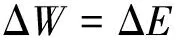
移项得

(1)

由焓的定义H=E+pΔV，上式可变为

令E1=ε1Δm，E2=ε2Δm，其中ε为单位质量气体内能，将上述条件代入式(1)可得

两边同除以Δm，有

即

(2)

式(2)是推导出的可压缩理想气体的伯努利方程[3].

(3)

式(3)就是推导出的等温条件下可压缩理想气体的伯努利方程.

2 比较分析

2.1 与不可压缩理想气体的伯努利方程比较

对于不可压缩理想气体(包括液体)，伯努利方程可表达为[4，5]

(4)

式(4)与式(3)从形式上看是不相同的.对于不可压缩的理想气体, 气体的质量密度ρ是一个常数,式(4)两边同除ρ,可得

(5)

在等温条件下，上式左边的第一项是常数，则式(5)就可变成式(3).也就是说，不可压缩理想气体在等温条件下的伯努利方程与等温条件下可压缩理想气体的伯努利方程在形式上是一致的.但两者在本质上是有区别的,不可压缩理想气体在等温条件下的压强和密度都是常数，而可压缩理想气体在等温条件下的压强和密度都可以变化，只是两者的比值为常数.

2.2 与等熵可压缩理想气体的伯努利方程比较

等熵过程是指流体与外界没有热量传递.一般认为，等熵过程适用于高速流动的可压缩理想气体，在高速流动过程中，流体来不及与外界进行热量交换.由泊松式以及pV=nRT，得

再结合欧拉方程，推导出[2,6]

(6)

其中，γ是定压摩尔热容和定体摩尔热容之比，又称为比热比.

比较式(6)和式(3)可知，等熵过程的伯努利方程比等温过程的伯努利方程左边多了一项.这两个过程的成立条件是不相同的，一个成立条件是等熵，另一个成立条件是等温，等熵过程中系统与外界没有能量交换，而等温过程可以有能量交换，故这两个方程在形式上不一样是合理的.

2.3 与等焓可压缩理想气体的伯努利方程比较

焓的定义式为H=E+pΔV，其中内能E是温度的函数，pΔV也是温度的函数.如果系统的温度不变，那么系统的焓也就不变，故等温条件也就是等焓条件，等温条件下可压缩理想气体的伯努利方程也就是等焓条件下可压缩理想气体的伯努利方程.

3 结论

本文从不可压缩的伯努利方程解释飞机升力模型出现的矛盾出发，通过理论分析，得出以下结果：

(1) 建立了可压缩理想气体的伯努利方程，并导出了等温条件下的简洁形式.

(2) 不可压缩理想气体在等温条件下的伯努利方程与等温条件下可压缩的伯努利方程方程在形式上是一致的,但本质上是有区别的.

(3) 等温条件与等焓条件是一致的，等温条件下可压缩理想气体的伯努利方程就是等焓条件下可压缩理想气体的伯努利方程.

[1] 李洪芳.热学[M].2版.北京：高等教育出版社，2001.

[2] 李复.可压缩条件下的伯努利方程[J].大学物理，2008，27(8)：15-18,27.

[3] Van Wylen G J, Sonntag R E. Fundamentals of classical thermodynamics[M]. New York： John Wiley and Sons Inc.， 1965.

[4] 张三慧.大学基础物理学上[M].2版.北京：清华大学出版社,2010.

[5] 严导淦.流体力学中的总流伯努利方程[J].物理与工程，2014,24(4)：47-53. Yan D G. The total flow Bernoulli equation in fluid mechanics[J]. Physics and Engineering. 2014, 24(4): 47-53.

[6] 庄礼贤,等.流体力学[M].2版.合肥:中国科学技术大学出版社，2009.

■

THE BERNOULLI’S EQUATION OF COMPRESSIBLE IDEAL GAS UNDER THE ISOTHERMAL CONDITION

Yu Jintao1Tao Zongming2

(1Third Brigade, Army Officer Academy, Hefei, Anhui 230031;2Department of Basic Sciences, Army Officer Academy, Hefei, Anhui 230031)

Bernoulli’s equation of incompressible fluid appeared to be a contradiction when explaining the lift force on wing of airplane. From this point of contradiction, the model of isothermal process of ideal gas was established in this paper, and the Bernoulli’s equation of compressible ideal gas under the isothermal condition was derived by using the law of conservation of energy. Through comparison and analysis, we knew that the Bernoulli’s equation of incompressible ideal gas had the same form as the Bernoulli’s equation of compressible ideal gas under the isothermal condition, but they were different in substance. Compared with Bernoulli’s equation under the isentropic condition, the two had different forms and were suitable for different situations. The isothermal condition was the same as the isenthalpic condition, so the form and substance of the Bernoulli’s equation were same in two conditions.

Bernoulli’s equation; the ideal gas; isothermal conditions; compressible condition

2015-10-04

俞锦涛，男，军校学员；陶宗明，男，教授，主要从事大学物理教学研究、激光雷达研制和激光雷达大气探测研究等.zmtao@aiofm.ac.cn

俞锦涛，陶宗明. 等温条件下可压缩理想气体的伯努利方程[J]. 物理与工程，2016，26(6)：72-74.