与圆锥曲线有关的几个最值问题的解决方法
江西省高安市灰埠中学 金锦花
与圆锥曲线有关的几个最值问题的解决方法
江西省高安市灰埠中学 金锦花
平面解析几何是一门研究点的运动变化规律的学科,圆锥曲线中的范围问题或最值问题较为常见,所涉及的知识面也较为广泛,是教师和学生都感觉较为棘手的一个难点。下面就几个常见的最值问题谈几个常见的解决方法。
一、圆锥曲线上的任一点与圆锥曲线对称轴上某一定点的距离的最值问题
求圆锥曲线上任一点到某一定点的距离的最值问题,可借助“点在曲线上”实现变量统一,将横纵坐标两个变量中的一个用另一个表示,构造关于其中一个坐标的二次函数求最值。
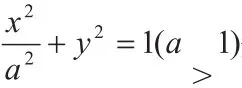
解:由题意,B点坐标为B(0,b)。设P(x0,y0),
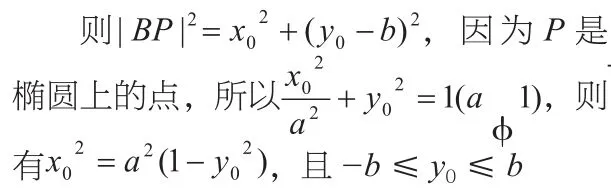

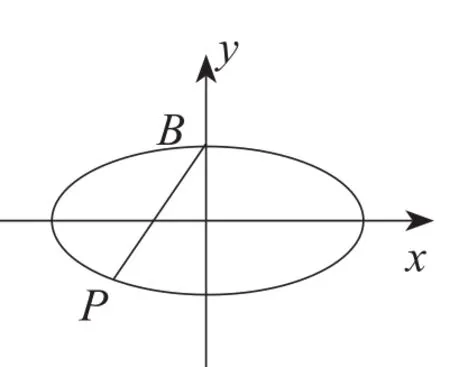
综上:略。
说明:在圆锥曲线上任一点到某一定点的距离的最值问题中,所给定点一般是圆锥曲线的对称轴上的点,否则变量统一往往比较困难。

该学生的解答是否正确?若正确,请写出他的解题依据;若不正确,请写出正确结果。
二、圆锥曲线上的任意点到某一定直线的距离的最值问题
求圆锥曲线上任一点到某一定直线的距离的最值,借助“点在曲线上”实现变量统一往往比较困难,这时可借助“切线平移法”实现变量统一或“三角代换”求最值。
例3 求抛物线y=-x2上的点到直线l:4x+3y-8=0距离的最小值。


解法二:(切线平移法)
设与直线l平行的直线l′的方程为:4x+3y+b=0,
则直线l平移到与抛物线相切时的切点Q即抛物线上到直线l最近的点,直线l与l′的距离即所求最小距离。


说明:在求椭圆或双曲线一支上的一点到一条定直线的距离的最值问题中,“变量统一”很难做到,在这种情况下,“切线平移法”就显得较为方便。
解法一:(切线平移法)设与直线l平行的直线的方程为:x-y+b=0,

解法二:(三角代换法)

说明:与圆、椭圆或双曲线有关的最值问题中,利用三角比中的平方关系实现变量统一也是平面解析几何中一种较为常见的方法。
通过前面几种常见最值问题的赘述可以看到,解析几何中的最值问题和以前所学过的知识是存在着一种紧密的内在联系的,只要我们能够深刻理解圆锥曲线的定义及方程所揭示的内涵,灵活运用数形结合的数学思想,就可以将问题转化为我们所熟悉的一些数学模型,将问题解决。

