基于仿射跳扩散模型的利率衍生品定价
汪嘉骎
(广西师范大学数学与统计学院,广西桂林541004)
基于仿射跳扩散模型的利率衍生品定价
汪嘉骎
,邓国和
(广西师范大学数学与统计学院,广西桂林541004)
本文考虑短期利率满足一类仿射跳扩散期限结构模型的利率衍生品定价。应用Fourier变换方法和远期测度技术,获到了零息票债券及基于零息票债券为标的资产的欧式债券期权价格的显示解,并将此结果应用于付息债券期权和利率期权的定价。最后,利用数值实例分别分析了债券和零息票债券期权价格受利率模型中各主要参数的影响,以及期权的隐含波动率问题。数值结果表明,跳跃风险参数对利率衍生品价格和隐含波动率有显著作用,这也验证了仿射跳扩散的利率期限结构模型具有较好拟合实际的能力。
仿射跳扩散模型;利率期限结构;债券期权;Fourier变换;隐含波动率
0 引言
利率是金融市场中最基本和最重要的经济变量之一,许多金融衍生工具(例如股票型期权、信用衍生品等)的定价和设计从根本上来说都依赖于利率的变化过程,金融理论与实际应用研究也离不开利率。利率模型(也称利率期限结构模型)是利率衍生品定价和风险管理的重要工具,没有利率理论模型,我们很难对许多实务问题做出合理的定价及寻找出理想的利率风险对冲策略,更无法进行利率产品的金融创新设计。因此,对它的研究一直是金融数学与计量金融理论的热点和难点。近年来,学者和业界投资者观察到利率市场上债券的收益率曲线(yield curve)和隐含波动率曲面(implied volatility surface)出现了比以往更复杂的变化特征。这表明需要引入更复杂、弹性更好的数学模型以描述和研究利率的运动及其衍生产品价格的波动。
现有的许多经典利率期限结构模型,例如Vasicek[1]模型、CIR[2]模型、Brennan和Schwartz[3]模型以及其他扩展的模型[4-8]均假设状态变量(例如短期利率、长期利率水平、波动率或其他)连续运动,且服从各种框架的连续形式扩散过程。尽管扩散过程在统计上有着良好的特性,并且计算方便,但越来越多的实证研究表明纯扩散过程并不完全适合描述金融状态变量(因为金融数据往往表现出尖峰厚尾特点,正态分布很难描述这类实际现象)。例如Hamilton[9],Das[10],Johannes[11],Piazzesi[12],Andersen、Benzoni和Lund[13],Jarrow、Li和Zhao[14]等的研究发现利率动态过程具有明显的跳跃特征存在。Lin和Yeh[15]研究了债券市场,发现跳跃扩散过程更加适合于描述利率过程。在定价和对冲金融衍生品时,跳跃扩散模型尤为重要,若忽视跳跃风险部分,将会引起金融产品的定价和对冲风险。因此,在描述利率的动态过程中引入跳跃风险因素更为重要。
由于20世纪70年代西方各国放宽对利率的监管,实行金融自由化政策,利率不确定性逐渐加剧,以致越来越多的金融机构和投资者面临利率风险的冲击。对冲和管理利率风险的有效工具——利率衍生品(interest rate derivatives)开始逐渐产生,并在市场上受到了欢迎。利率衍生品是一种损益以某种方式依赖于利率水平变化的金融创新工具,市场上交易的产品类型很多,交易规模庞大,债券期权(bond options)就是一类重要的利率衍生工具,其买卖的标的物是某一种债券(比如零息票债券、付息债券、违约债券等)。由于利率的动态变化,债券期权的定价比股票期权的定价更复杂。不同利率模型下的债券期权定价数学方法与计算也不尽相同。目前,关于债券期权的定价均是建立在利率满足扩散过程驱动的期限结构模型,研究成果丰富(如文献[16]),但在利率的跳扩散模型下研究较少。Ahn和Thompson[17]首次将CIR[2]模型扩展为带有跳跃部分的平方根利率过程(记为JCIR模型),并应用线性化技术获得了零息票债券的闭式解。Shirakawa[18]首次在利率跳扩散模型下开展债券期权定价研究,他们均假设短期利率具有有限个非随机的跳跃振幅。后来,Baz和Das[19]在Vasicek[1]模型中加入跳跃部分扩展了纯扩散利率过程(记为JVasicek模型),并设定利率的跳跃振幅服从正态分布,应用文献[17]的近似技术获得了零息票债券价格。Das和Foresi[20]也扩展了Vasicek[1]模型,并允许利率的跳跃振幅服从双指数分布,获得了零息票债券及债券期权的价格。Das[21-22]、Finnerty[23]推广了Hull-White[4]模型,并设定利率的跳跃振幅服从正态分布或其他分布,同样地获得了零息票债券及债券期权的价格。最近,Beliaeva[24]、Nawalkha[25]和Deng[26]等在利率的跳扩散模型下研究了美式债券期权的定价方法。上述研究的一个共同点是假设利率动态过程满足某个特定的跳扩散模型,在实际应用过程中存在不足(比如,JVasicek模型可能导致利率出现负值,JCIR模型仅限于利率的正向跳跃风险,等)。为了更加全面较准确地描述利率的动态行为特征,本文综合上述利率的跳扩散模型,考虑一类更为广泛的仿射跳扩散过程(此过程由Duffie等人[27]提出,在描述股价运动行为,及在股票型期权定价研究方面已有广泛应用)驱动利率的动态行为(记为JCIR-Ex模型),该模型不仅融合了JVasicek和JCIR跳扩散模型的优点,也克服了这两个模型的不足,并且还能突现利率波动率的时变特征。本文的主要贡献为: 首先,利用仿射跳扩散过程的特点建立短期利率行为的动力学模型,该模型中利率的波动率受内部和外部因素的影响,且不同于JVasicek和JCIR跳扩散模型,并建立基于利率变量的任何欧式未定权益满足的偏微分-积分方程,利用仿射结构特点,获得零息票债券价格的显示解。其次,应用Fourier反变换方法和远期概率测度技术,研究欧式零息票债券期权的定价,并将结果应用于付息债券期权和利率期权的定价,分别获得这些期权价格计算的显示公式,为金融风险管理(如对冲策略的计算)提供便利。最后,给出数值计算实例,分析该利率模型中跳跃风险因素对债券和债券期权价格的影响,以及债券期权的隐含波动率(即微笑现象)问题。
1 利率模型与债券价格
考虑一个无套利,无摩擦,且可连续进行交易的经济体,交易有限期限为τ=[0,T*],T*<∞。该经济体中所有不确定性因素均定义在一个带有信息滤波的给定完备概率空间(Ω,F,(Ft)t∈τ,Q)中,其中Q是风险中性概率测度,信息滤波(Ft)t∈τ为满足通常条件的完备参考族。假定在风险中性概率Q下,瞬时利率rt的运动行为满足下列仿射跳扩散模型:
(1)
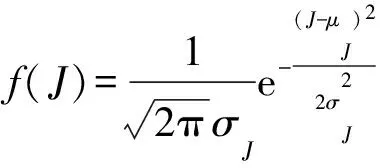
为方便起见,记模型(1)为JCIR-Ex模型。该模型包括了现有一些应用广泛的瞬时利率模型:(ⅰ)如果模型中参数α=β=λ=0,则式(1)变为确定性利率变动模型。(ⅱ)如果模型中参数α=λ=0且β>0,则式(1)变为Vasicek[1]模型。(ⅲ)如果模型中参数β=λ=0且α>0,则式(1)变为CIR[2]模型。(ⅳ)当参数α=0且β>0,则式(1)变为JVasicek模型[19];当参数α>0且β=0,则式(1)变为JCIR模型[17]。
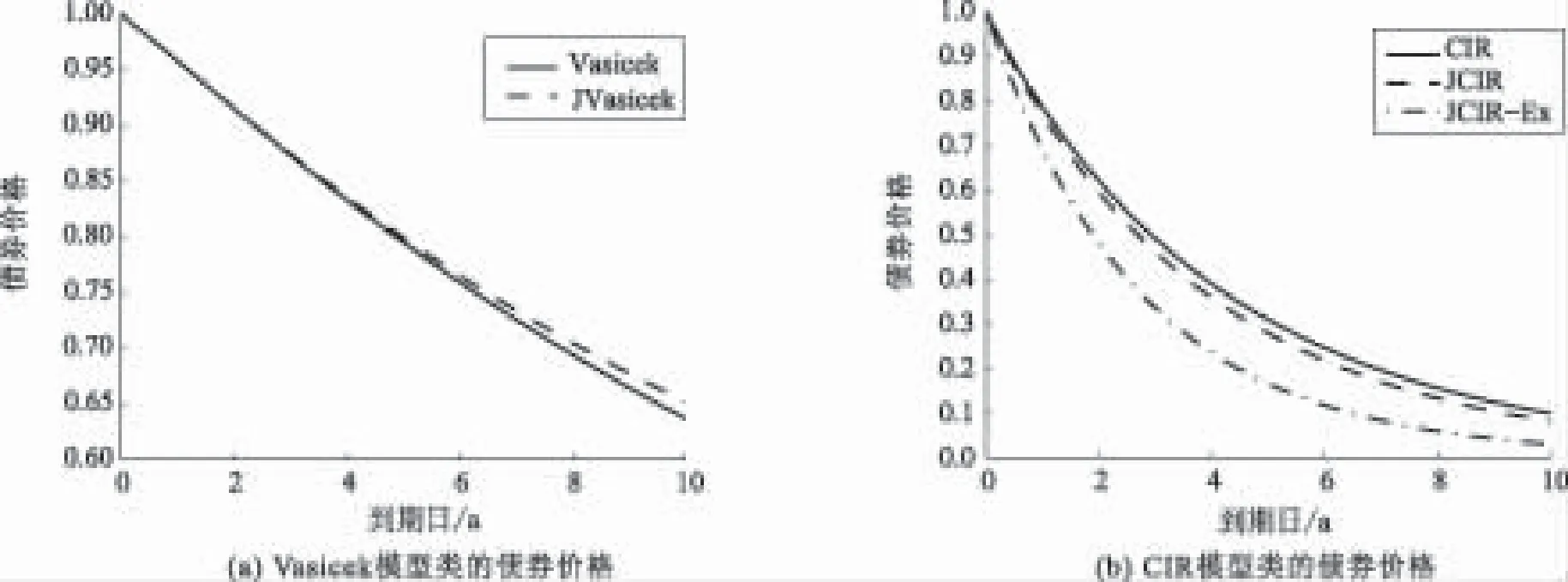
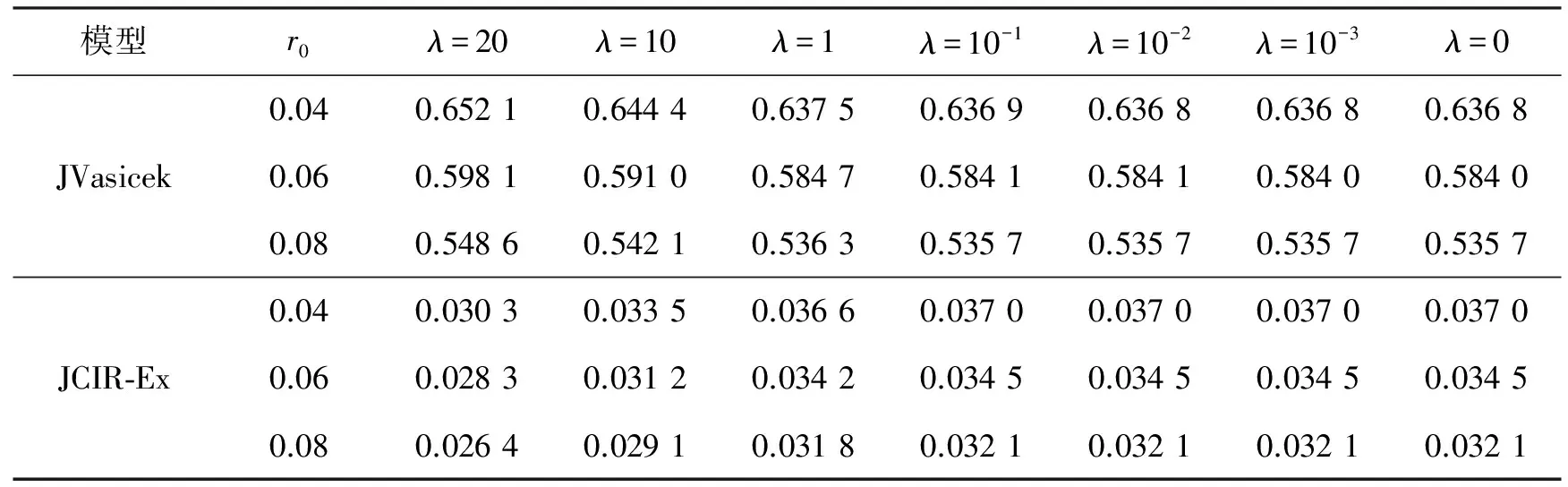
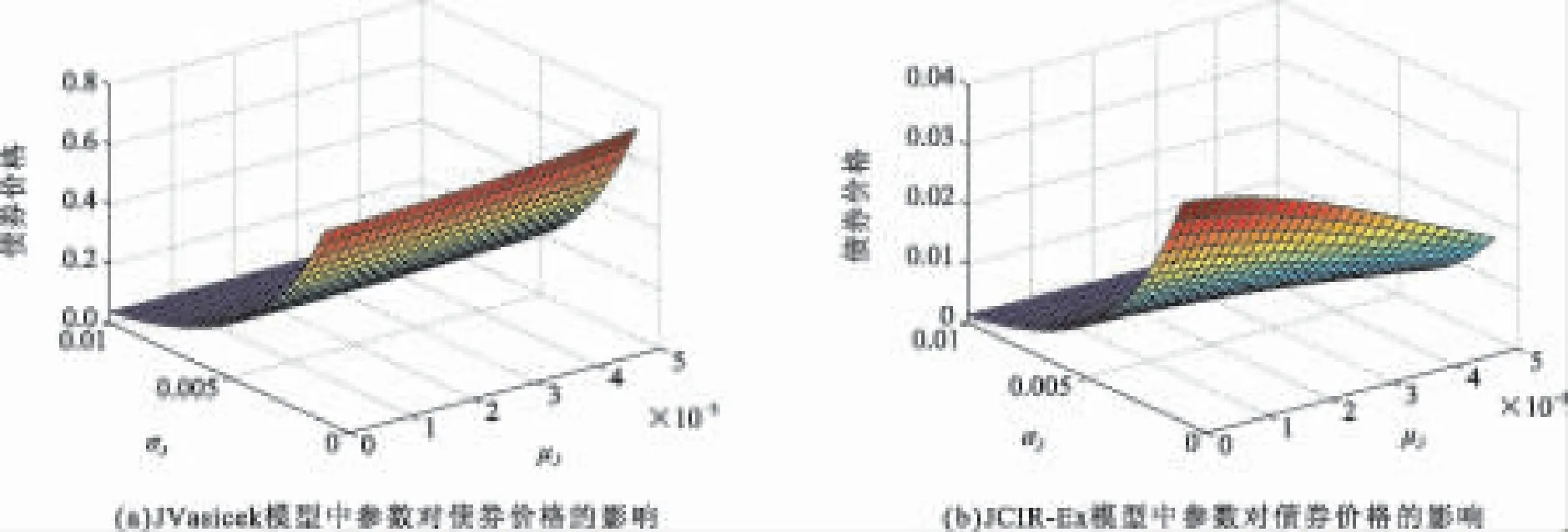
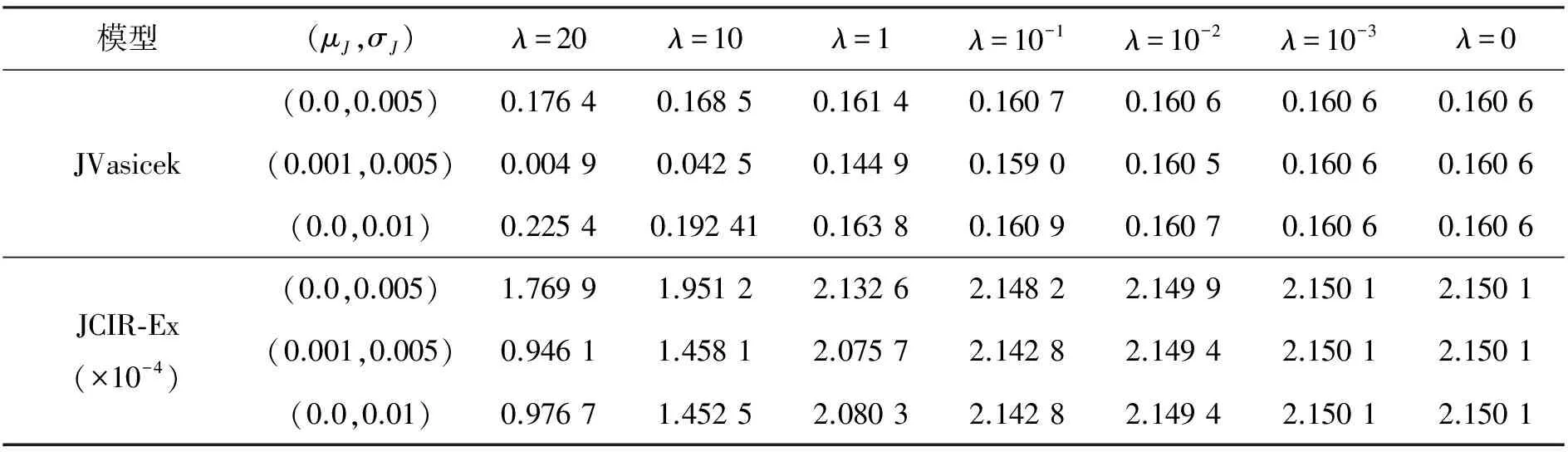
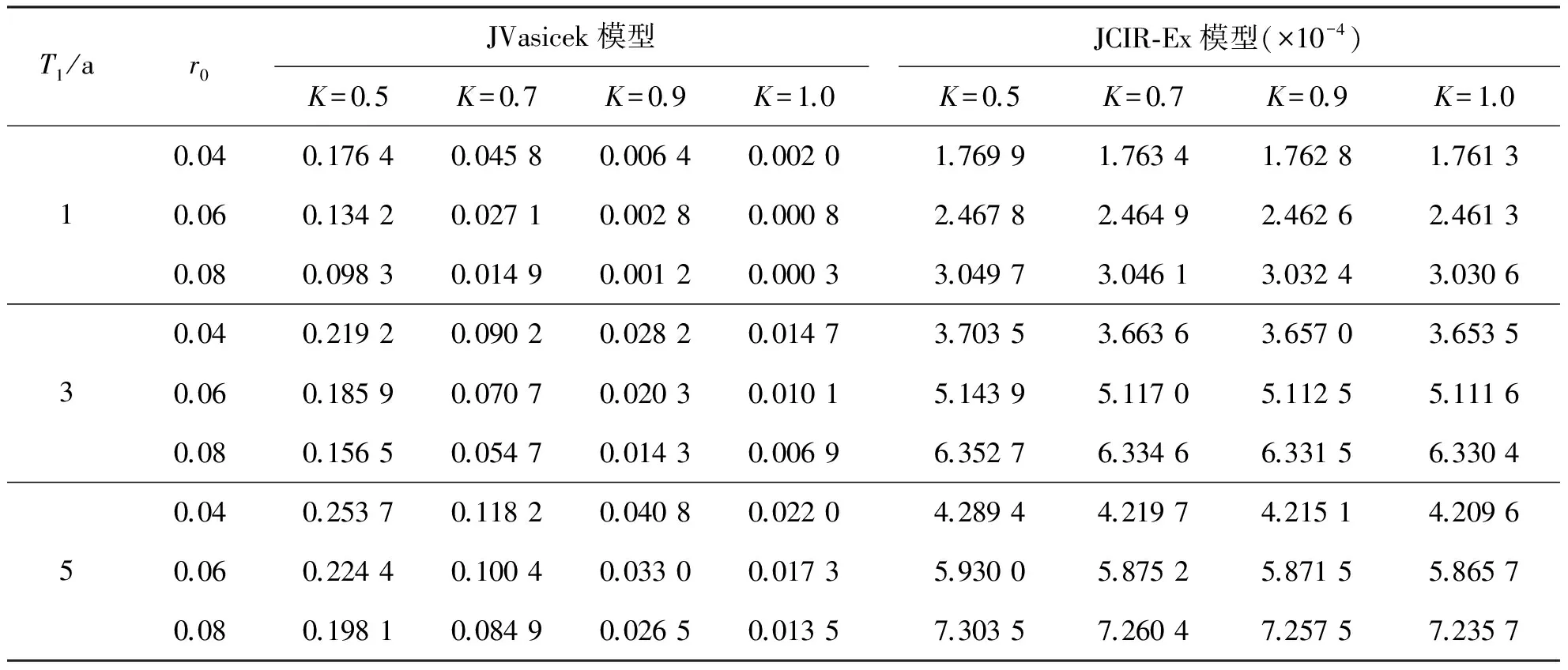
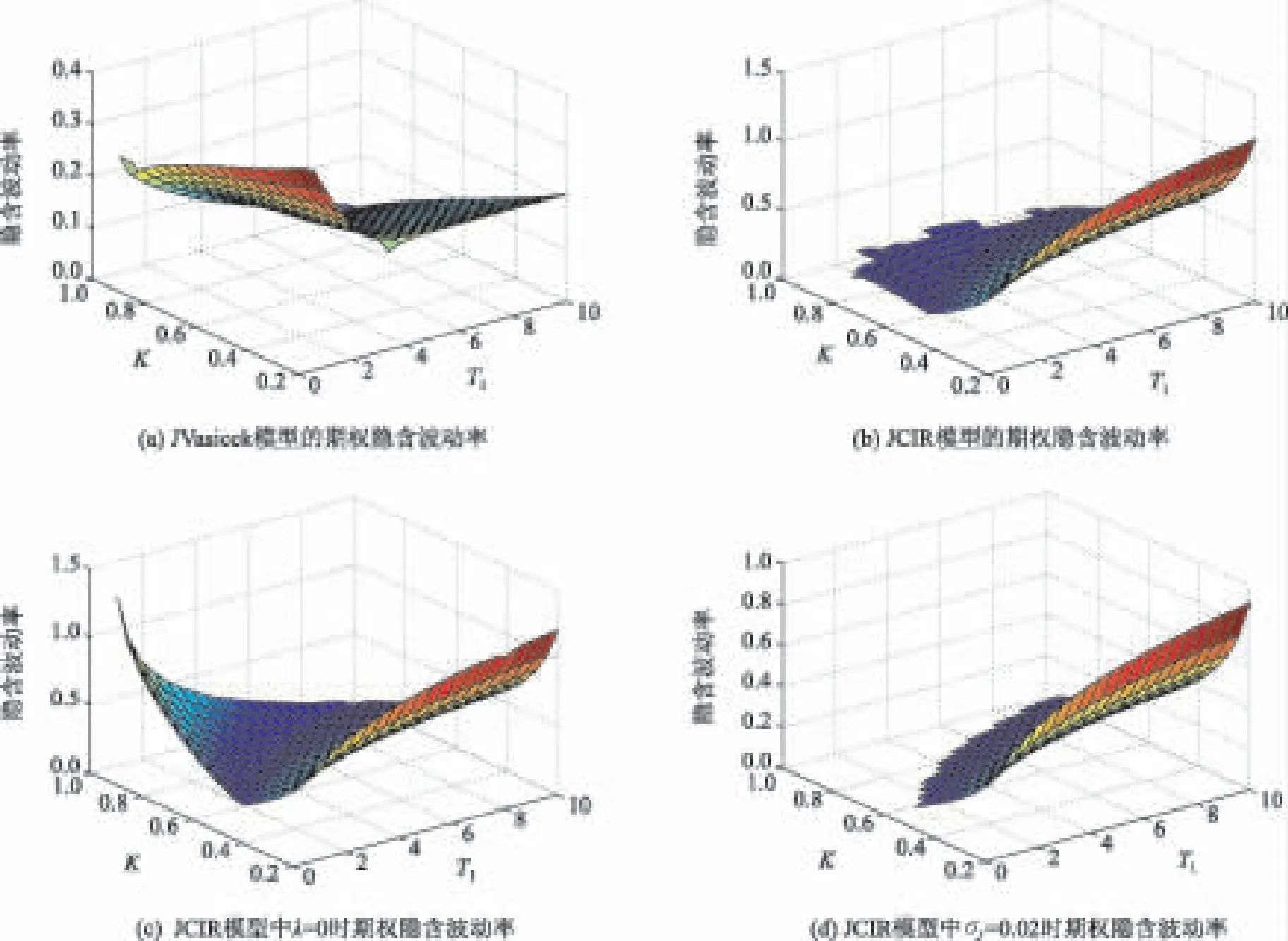
按照风险中性定价原理,该经济体中所有交易证券的折现过程是(Ω,Ft)-鞅过程。记该经济体中到期期限为T (2) F(T,r,T)=h(r), (3) 其中微分算子L定义为: 下面给出零息票债券的定价。记零息票债券t≤T时刻价格为P(t,r,T)。显然,零息票债券在到期日T时的收益等于1,即P(T,r,T)=1,亦即H(rT)=1。于是由式(2)可得 (4) 为了计算债券及其衍生品的价格,先给出引理如下。 引理1 设短期利率rt满足模型(1)。于是,对任意满足exp{zr}有界的z∈C,复Fourier变换: (5) 具有显示表达式exp{A(t,T,z)+B(t,T,z)rt},其中: (6) (7) 比较状态变量前的系数,进一步得到A(t,T,z)与B(t,T,z)分别满足下列常微分方程: (8) (9) 现求解方程(9)。分两种情形:α≠0和α≡0考虑。 (10) 利用Riccati方程理论,易得D具有表达式 (11) 将式(11)回代得B的表达式。 由于方程(9)中含有积分项,为了获得系数A(t,T,z)的封闭式解,这里采用文献[17]或文献[19]中同样的线性化技术近似方程(9)中的积分项,即应用2阶Taylor展开积分项中的指数函数: 于是 现令z≡0,并记τ=T-t,则零息票债券的价格为: 引理2T-期零息票债券t时刻的价格,P(t,r,t+τ),t P(t,r,t+τ)=exp{a(τ)+b(τ)rt}, (12) 其中a(τ)=A(t,T,0),b(τ)=B(t,T,0)。 本节考虑标的资产为零息票债券的欧式未定权益的定价。首先给出欧式零息票债券看涨期权的价格,再应用欧式零息票债券看涨期权的价格研究付息债券期权及利率期权的定价。记欧式零息票债券看涨期权的到期日为T1( (13) 并且有: 定理1 设短期利率rt满足模型(1),则 Ce(t,r,T1,T,K)=P(t,r,T)Π1-KP(t,r,T1)Π2, (14) φ1(u)=ea(T-T1)-a(τ)-b(τ)rΨ(t,T1,r,(iu+1)b(T-T1)), φ2(u)=e-a(T1-t)-b(T1-t)rΨ(t,T1,r,iu,b(T-T1)), R[·]表示[·]的实部,i是虚数单位。 证明 由式(13)可知 (15) (16) 容易验证 测度Q1和Q2都是概率测度Q的等价鞅概率测度。因此,在新的概率测度Q1和Q2下,式(15)可写成: Ce(t,r,T1,T,K)=P(t,r,T1)Q1(lnP(T1,r,T)≥lnK)- KP(t,r,T)Q2(lnP(T1,r,T)≥lnK)=P(t,r,T1)Π1-KP(t,r,T)Π2, (17) 其中Πj=Qj(lnP(T1,r,T)≥lnK)=Qj(b(T-T1)rT1≥K*),j=1,2,且应用Fourier反变换法,有 (18) 这里φj(u),j=1,2是随机变量b(T-T1)rT1分别在Q1和Q2下的特征函数。 下面计算在原概率测度Q下的特征函数φj(u),j=1,2。由式(16)得: ea(T1,T)-a(t,T)-b(t,T)rΨ(t,T1,r,(iu+1)b(T-T1)) (19) 以及 e-a(T1-t)-b(T1-t)rΨ(t,T1,r,iub(T-T1))。 (20) 类似容易证明,执行价格为K,到期日为T1的欧式零息票债券看跌期权t时刻的价格为: 下面将欧式零息票期权定价的结果应用于付息债券期权和利率期权的定价。 (21) 注2 式(21)表明付息债券看涨期权的价格是由零息票债券看涨期权价格的加权总和。 证明 因为 (22) (23) 再由定理1得证。证毕。 (Ⅱ)利率期权(interest-rateoption)是一种与利率变化挂钩的期权,到期时以现金或者与利率相关的合约(如利率期货、远期利率或者政府债券)进行结算。最早在场外市场交易的利率期权是1985年推出的利率上限期权(interest-rateCaps)。目前,利率期权除利率上限期权合约外,还有利率下限期权(interest-rateFloors),利率双限期权(interest-rateCollars),利率互换期权(Swaps)等。这里仅给出利率下限期权的定价,其他产品的定价可类似证明。利率下限期权是由一系列的利率看跌期权(Floorlet)组合而成,而利率看跌期权的收益依赖于在时间t( (24) 定理3 在短期利率rt满足模型(1)下,则欧式利率看跌期权t(t (25) 证明 由式(24)及条件期望的迭代性质知: (26) (27) 注3 由定理3,很容易推导欧式利率上限期权(CapOption)和利率互换期权(Swaps)的定价公式分别为: 本节应用数值计算实例考察仿射跳扩散利率模型(1)下债券及其标准欧式看涨期权的价格影响因素。首先,分析债券价格分别在JVasicek与JCIR-Ex利率期限结构模型下对跳跃风险因素的性能表现,并分别与纯扩散过程的Vasicek和CIR利率期限结构模型的结果进行比较。其次,分别在JVasicek与JCIR-Ex模型下研究欧式零息票债券看涨期权的价格受参数影响的变动情况。最后,讨论债券期权的隐含波动率问题。数值计算选用Matlab 8.0软件编程在Intel(R) Core(TM) i5-2500 CPU 3.30 GHz,4 GB RAM的联想计算机上实现。模型(1)部分参数值来源于文献[21](见表1)。 表1 模型(1)中基本参数值选择 3.1 跳跃风险参数对债券价格的影响 图1 纯扩散模型与跳扩散模型下零息票债券价格之比较Fig.1 Comparison of bond price from the Pure-diffusion and Jump-diffusion model 图1考察了到期期限为10年的零息票债券价格分别在纯扩散和跳扩散的利率期限结构模型下的变动情况。图1(a)选取参数α=0,β=0.002 5时比较了Vasicek利率模型与带跳的Vasicek(即JVasicek)利率模型的债券价格。图1(b)选取参数α=0.04,β=0或β≠0时比较了CIR利率模型与带跳的CIR(即JCIR-Ex)利率模型的债券价格。计算结果表明:债券价格是期限值的减函数。另外,随着期限的增加,JVasicek模型下的债券价格越来越高于纯扩散过程驱动的Vasicek模型,这说明跳跃风险对债券价格有正向影响,但JCIR或JCR-Ex模型下的债券价格却越来越低于纯扩散过程驱动的CIR模型,跳跃风险对债券价格的作用是反向的。这是因为Vasicek利率模型服从正态分布,随着期限的增加且跳跃风险的存在,导致利率变小的机会增大,而CIR利率模型是服从卡方分布的,期限的增加与跳跃风险的存在,促使利率值快速增加。 表2 债券价格对利率初始值及跳跃强度的依赖性 表2研究了利率初始值r0及跳跃强度λ对债券价格影响。显然,在模型其他参数值不变的情形下,债券价格随着利率初始值的增加而减少。此外,对于JVasicek利率模型债券价格随着跳跃强度λ值减少而减少,且快速收敛到Vasicek模型时的债券价格,但对于JCIR-Ex利率模型债券价格则随着λ的减少快速增大收敛到CIR模型的价格。这表明了跳跃强度参数λ对债券价格有显著的影响,且对Vasicek与CIR利率期限结构模型的债券收益有不同的影响效果。与此同时,在模型参数值相同情形下,JVasicek模型下的债券价格比JCIR-Ex模型下的债券价格要大得多,两者相差近25倍,这是因为JVasicek模型下的利率值要小。 图2 JVasicek模型与JCIR-Ex模型下参数μJ和σJ对零息票债券价格的影响Fig.2 Sensitivities of both JVasicek model and JCIR-Ex model for the bond price with μJ and σJ 图2考查了债券价格依赖利率跳跃幅度参数μJ和σJ的敏感性。图2(a)、(b)分别绘制了JVasicek模型与JCIR-Ex模型下债券价格随参数μJ和σJ的变化情况。从图示可以看出,跳扩散模型下的债券价格均是利率跳跃幅度参数σJ的减函数,但参数μJ在JVasicek模型与JCIR-Ex模型下对债券价格的影响是反向的。 3.2 期权价格的参数依赖性 表3分别考查了JVasicek模型和JCIR-Ex模型中的跳跃风险参数λ、μJ和σJ对债券期权价格的影响,计算基本参数值见表1,这里选择K=0.5,T1=1 a。从表中可以看出,欧式零息票债券看涨期权价格是利率跳跃振幅的期望μJ的减函数。对于JVasicek利率模型,债券期权的价格是利率跳跃振幅的方差σJ的增函数,但对于JCIR-Ex利率模型,结果却相反。另外,一个有趣的发现:在JVasicek模型与JCIR-Ex模型中,利率跳跃振幅的期望μJ大小会影响跳跃强度参数λ对债券期权价格的作用效果。例如,在JVasicek模型中,当μJ=0时,债券期权价格是跳跃强度参数λ的增函数,但μJ≠0时,债券期权价格反而是跳跃强度参数λ的减函数。另一方面,在JCIR-Ex模型中,债券期权价格均是跳跃强度参数λ的减函数,且不受μJ值的影响。 表3 跳跃风险参数对零息债券看涨期权价格的影响 表4 JVasicek模型与JCIR-Ex模型下不同T1、r0和K值的零息票债券欧式看涨期权价格 表4考查了标准欧式零息票债券看涨期权在JVasicek模型与JCIR-Ex模型下随着T1、r0和K值变化时的价格。模型(1)计算的基本参数值见表1,选取利率初始值r0=0.04,0.06,0.08,期权到期日T1=1,3,5 a,以及期权执行价K=0.5,0.7,0.9,1.0分别计算,结果见表4。从表中可以看出,零息票债券看涨期权价格随着执行价格K的增大(从价内期权变化到价外期权)而减少,这与股票型看涨期权的变化趋势一致,并且期权价格是T1的增函数。另外,当短期利率满足JVasicek模型时,零息票债券看涨期权价格随着r0的增加而变小;然而,当短期利率满足JCIR-Ex模型时,零息票债券看涨期权价格却随着r0的增加而变大。此外,JVasicek模型与JCIR-Ex模型下的标准欧式零息票债券看涨期权价格相差很大,这表明JCIR-Ex模型比JVasicek模型在刻画债券价格方面具有更小的波动或低债券价格(与表2、图2的分析结果一致)。 3.3 债券期权的隐含波动率 金融市场通常以隐含波动率(implied volatility)的方式来引用看涨或看跌期权的价格变化。实际上,金融市场交易的欧式看涨期权的隐含波动率曲面依赖于期权敲定价格K和到期时间T。对相同的到期时间T,表现出波动率微笑/倾斜(smile/skew)特性,而且随着时间演变,隐含波动率的曲面也在变动。隐含波动率问题已引起了业界和学术界对期权定价模型的推广。下面分析仿射跳扩散利率模型下债券期权的隐含波动率问题,数值计算参数见表1。图3(a)和(b)分别刻画了JVasicek模型与JCIR-Ex模型下期权的隐含波动率变化。从隐含波动率的微笑曲面可以看出,仿射跳扩散的利率期限结构模型具有较好拟合实际的能力,这与文献[10,15]的实证结果一致。另外,从图示还可以发现:①JVasicek模型下债券期权的隐含波动率要比JCIR-Ex模型下的小很多,且表现出较平坦;②期权到期期限短的隐含波动率的微笑现象比较显著;③JVasicek模型下债券期权的隐含波动率是期权到期日T1的减函数,而JCIR-Ex模型下债券期权的隐含波动率却是期权到期日T1的增函数。 图3 仿射跳扩散模型下债券期权的隐含波动率Fig.3 Implied volatilities of bond options in affine jump-diffusion model 图3(c)和(d)在JCIR-Ex模型下分别考察跳跃强度参数λ=0及跳跃幅度的波动率σJ=0.02时的隐含波动率曲面。通过比较图3(b)和(c)可以发现,跳跃强度参数对债券期权的隐含波动率影响很大,特别是在λ=0时(无跳跃风险)债券期权的隐含波动率微笑现象显著,这也表明引入跳跃风险因素来捕捉市场利率的突发信息到达引发的利率剧烈波动是合理可行的。另外,图3(b)和(d)表明JCIR-Ex模型下利率跳跃幅度的波动率对债券期权的隐含波动率的影响显著,大波动率导致隐含波动率曲面更倾斜。 本文在一类仿射跳扩散利率期限结构模型下应用Fourier变换方法和远期测度技术获得了债券及债券期权的价格显示解,并应用数值实例分析了模型中跳跃风险参数对债券或期权价格的影响。数值计算结果表明,跳扩散过程驱动的利率期限结构模型对利率衍生品的影响具有不同作用,也说明在连续的纯扩散模型中引入不连续运动的跳跃风险因素是必须的,且具有较好的拟合实际能力。本文仅在利率满足单因素情形下研究利率衍生品的定价,模型还可以进一步扩展到多因素情形的跳扩散过程(如文献[27]),以及研究其他利率衍生品的定价,这将是未来研究重点。 [1] VASICEK O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics,1977,5(2): 177-188. DOI:10.1016/0304-405X(77)90016-2. [2] COX J C,INGERSOLL J E,ROSS S A. A theory of the term structure of interest rates[J]. Econometrica,1985,53(2): 385-407. DOI:10.2307/1911242. [3] BRENNAN M J,SCHWARTZ E S. A continuous time approach to the pricing of bonds[J]. Journal of Banking and Finance,1979,3(2): 133-155. DOI:10.1016/0378-4266(79)90011-6. [4] HULL J,WHITE A. Pricing interest-rate-derivative securities[J]. The Review of Financial Studies,1990,3(4): 573-592. DOI:10.1093/rfs/3.4.573. [5] HEATH D,JARROW R,MORTON A. Bond pricing and the term structure of interest rates: a new methodology for contingent claims valuation[J]. Econometrica,1992,60(1): 77-105. DOI:10.2307/2951677. [6] CHEN R R,SCOTT L. Pricing interest rate options in a two-factor Cox-Ingersoll-Ross model of the term structure[J]. The Review of Financial Studies,1992,5(4): 613-636. DOI:10.1093/rfs/5.4.613. [7] BANSAL R,ZHOU Hao. Term structure of interest rates with regime shifts[J]. The Journal of Finance,2002,57(5): 1997-2043. DOI:10.1111/0022-1082.00487. [8] DUFFIE D,KAN R. A yield-factor model of interest rates[J]. Mathematical Finance,1996,6(4): 379-406. DOI:10.1111/j.1467-9965.1996.tb00123.x. [9] HAMILTON J D. Rational-expectations econometric analysis of changes in regime: an investigation of the term structure of interest rates[J]. Journal of Economic Dynamics and Control,1988,12(2/3): 385-423. DOI:10.1016/0165-1889(88)90047-4. [10] DAS S R. The surprise element: jumps in interest rates[J]. Journal of Econometrics,2002,106(1): 27-65. DOI:10.1016/S0304-4076(01)00085-9. [11] JOHANNES M. The statistical and economic role of jumps in continuous-time interest rate models[J]. The Journal of Finance,2004,59(1): 227-260. DOI:10.1111/j.1540-6321.2004.00632.x. [12] PIAZZESI M. Bond yields and the federal reserve[J]. Journal of Political Economy,2005,113(2): 311-344. DOI:10.1086/427466. [13] ANDERSEN T,BENZONI L,LUND J. Stochastic volatility,mean drift,and jumps in the short-term interest rate[R]. Chicago: Northwestern University, 2004. [14] JARROW R,LI Haitao,ZHAO Feng. Interest rate caps "smile" too! But can the LIBOR market models capture the smile?[J]. The Journal of Finance,2007,62(1): 345-382. DOI:10.1111/j.1540-6261.2007.01209.x. [15] LIN B H,YEH S K. Jump-diffusion interest rate process: an empirical examination[J]. Journal of Business Finance and Accounting,1999,26(7/8): 967-995. DOI:10.1111/1468-5957.00282. [16] 陈松男. 利率衍生品设计原理与应用: 案例分析[M]. 北京: 机械工业出版社,2014. [17] AHN C M,THOMPSON H E. Jump-diffusion processes and the term structure of interest rates[J]. The Journal of Finance,1988,43(1): 155-174. DOI:10.1111/j.1540-6261.1988.tb02595.x. [18] SHIRAKAWA H. Interest rate option pricing with Poisson-Gaussian forward rate curve process[J]. Mathematical Finance,1991,1(4): 77-94. DOI:10.1111/j.1467-9965.1991.tb00020.x. [19] BAZ J,DAS S R. Analytical approximations of the term structure for jump-diffusion process: a numerical analysis[J]. The Journal of Fixed Income,1996,6(1): 78-86. DOI:10.3905/jfi.1996.408164. [20] DAS S R,FORESI S. Exact solutions for bond and option prices with systematic jump risk[J]. Review of Derivatives Research,1996,1(1): 7-24. DOI:10.1007/BF01536393. [21] DAS S R. Discrete-time bond and option pricing for jump-diffusion processes[J]. Review of Derivatives Research,1996,1(3): 211-243. DOI:10.1007/BF01531143. [22] DAS S R. A direct discrete-time approach to Poisson-Gaussian bond option pricing in the Heath-Jarrow-Morton model[J]. J Econ Dyn Control,1998,23(3): 333-369. DOI:10.1016/S0165-1889(98)00031-1. [23] FINNERTY J D. Exact formulas for pricing bonds and options when interest rate diffusions contain jumps[J]. The Journal of Financial Research,2005,28(3): 319-341. DOI:10.1111/j.1475-6803.2005.00127.x. [24] BELIAEVA N A,NAWALKHA S K,SOTO G M. Pricing American interest rate options under the jump-extended Vasicek model[J]. Journal of Derivatives,2008,16(1): 29-43. DOI:10.3905/jod.2008.710896. [25] BELIAEVA N,NAWALKHA S K. Pricing American interest rate options under the jump-extended constant-elasticity-of-variance short rate models[J]. Journal of Banking & Finance,2012,36(1): 151-163. DOI:10.1016/j.jbankfin.2011.06.012. [26] DENG Guohe. Pricing American put option on zero-coupon bond in a jump-extended CIR model[J]. Commun Nonlinear Sci Numer Simulat,2015,22(1/2/3): 186-196. DOI:10.1016/j.cnsns.2014.10.003. [27] DUFFIE D,PAN Jun,SINGLETON K. Transform analysis and asset pricing for affine jump-diffusions[J]. Econometrica,2000,68(6): 1343-1376. DOI:10.1111/1468-0262.00164. [28] GEMAN H, KAROUI N E,ROCHET J C. Changes of numeraire,changes of probability measures and option pricing[J]. Journal of Applied Probability,1995,32(2): 443-458. DOI:10.2307/3215299. (责任编辑 黄 勇) Pricing of Interest Rate Derivatives Based on Affine Jump Diffusion Model WANG Jiaqin, DENG Guohe (School of Mathematics and Statistics,Guangxi Normal University, Guilin Guangxi 541004, China) The pricing of interest rate derivatives is considered under an affine jump diffusion model. Using the Fourier transform method and the forward measure change technique,the closed explicit formulas for both the price of the default-free,zero-coupon bond and the value of the European options on the default-free,zero-coupon bond are obtained. Furthermore,pricing problems on both the European option on the coupon bond and the interest rate options are extended in this model by applying these explicit formulas above. Finally,the impacts of the key parameters in this model on prices for both the bond and bond option,and implied volatilities of bond options are analyzed by numerical examples,respectively. Numerical results show that the jump risks have more remarkable effects on the interest rate derivative prices and implied volatility,which show that the affine jump diffusion term structure model of the interest rate fits reality well. affine jump diffusion model;term structure of interest rate;bond options;Fourier transform;implied volatility. 10.16088/j.issn.1001-6600.2016.03.011 2016-03-01 国家自然科学基金资助项目(11461008);教育部人文社会科学研究规划基金资助项目(13YJA910003);广西自然科学基金资助项目(2013GXNSFAA019005);广西高等学校科学技术研究重点项目(2013ZD010) 邓国和(1969—),男,湖南桂阳人,广西师范大学教授,博士. E-mail:dengguohe@mailbox.gxnu.edu.cn O211.9 A 1001-6600(2016)03-0074-12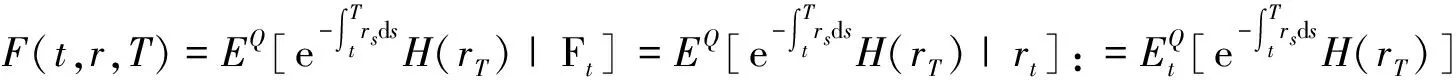

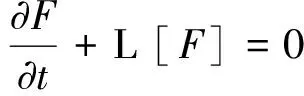
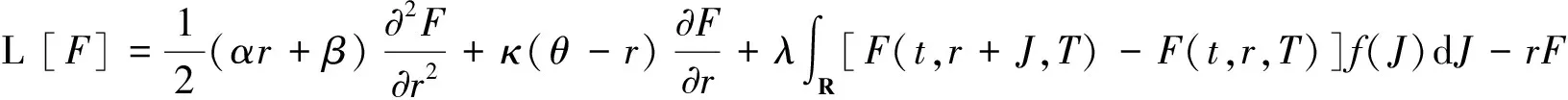
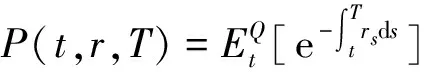
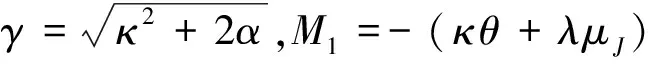

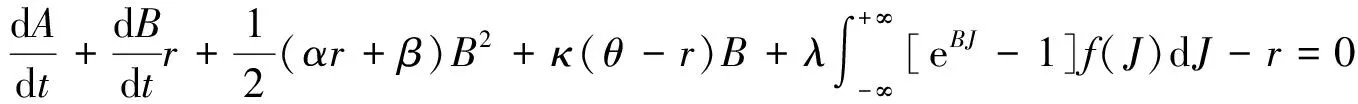
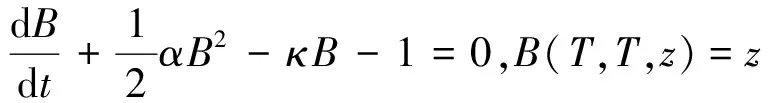
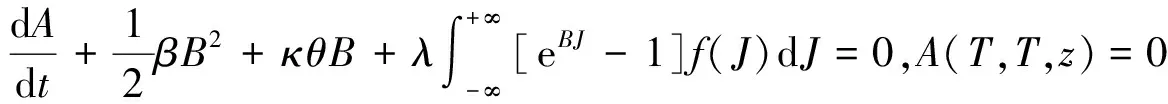
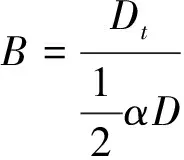
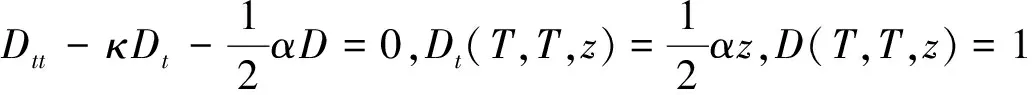
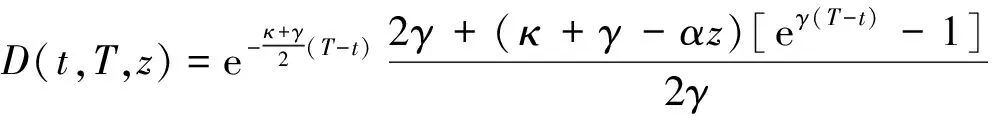
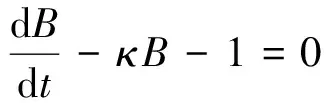
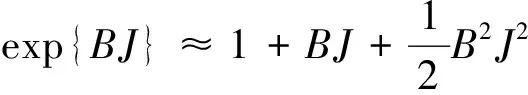
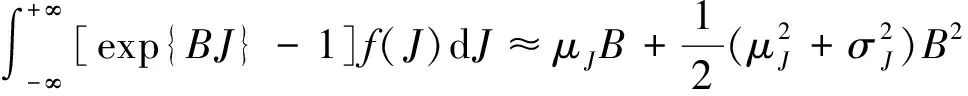
2 债券期权定价
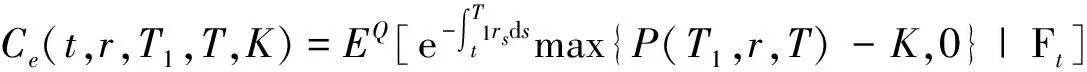
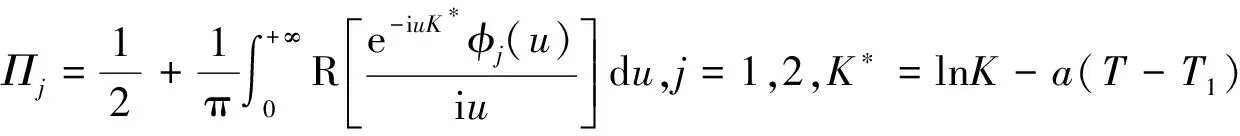
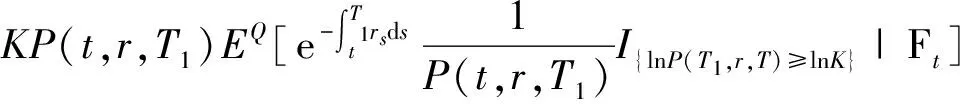

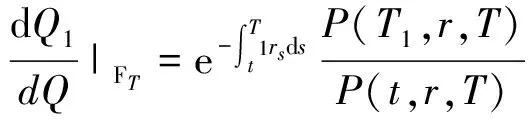
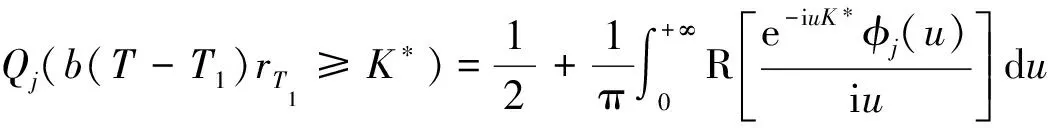
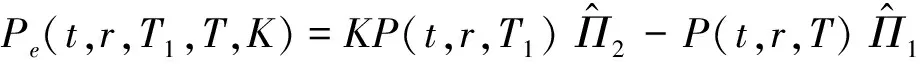
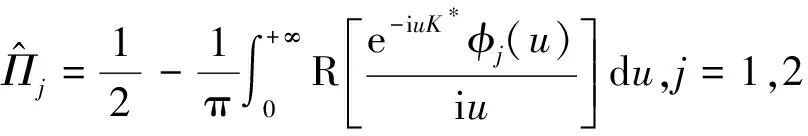
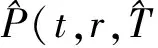
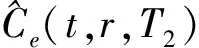
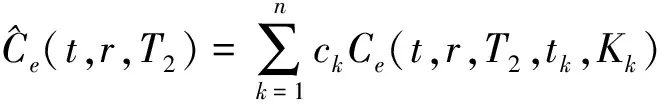
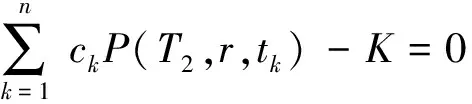
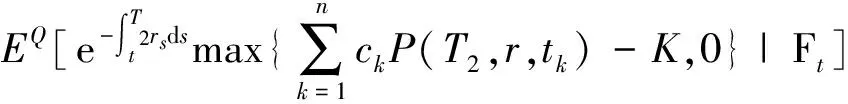
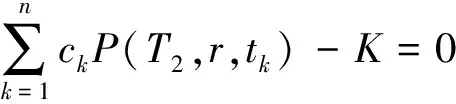
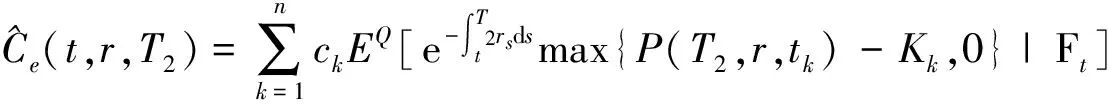
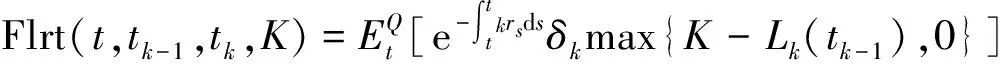
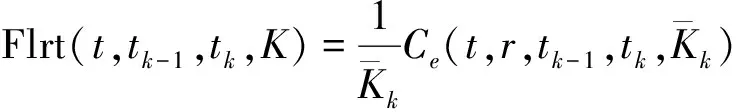
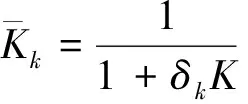
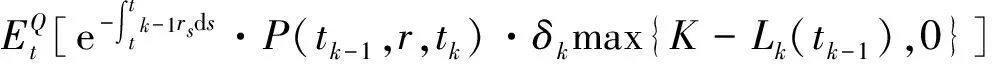
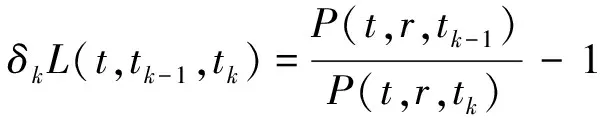
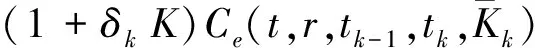
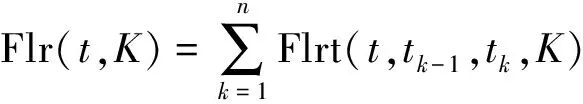
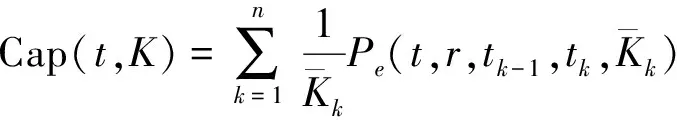
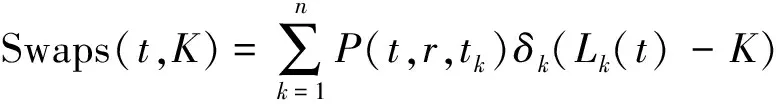
3 数值结果与分析

4 结论

