BES III上J/ψ→γηc→γφφ的蒙特卡罗模拟

廖广睿，杨永栩

(广西师范大学物理科学与技术学院，广西桂林541004)



BES III上J/ψ→γηc→γφφ的蒙特卡罗模拟

廖广睿，杨永栩

(广西师范大学物理科学与技术学院，广西桂林541004)

本文利用BES III的离线软件系统，对J/ψ→γηc→γφφ进行蒙特卡罗模拟，通过比较单举道和遍举道蒙特卡罗样本，对末态粒子进行筛选，选择效率是BES II的1.5倍；同时，得到的衰变道ηc→φφ的分支比在误差范围内与蒙特卡罗的输入值一致。根据目前BES III上J/ψ样本的统计量，按照本文提出的方案，预计可以得到2 144±26个ηc→φφ的事例。利用螺旋度的分析方法计算出各级衰变粒子在其母粒子坐标系下的角分布，遍举道蒙特卡罗的拟合结果与理论计算结果在误差范围内一致。本文的测量结果对实验上高精度测量该衰变道及BES III上实验数据分析具有重要意义。

分支比；蒙特卡罗模拟；螺旋度角分布

粲夸克是标准模型中6类夸克(上夸克、下夸克、奇异夸克、粲夸克、顶夸克和底夸克)之一。粲夸克和它的反夸克组成的粲偶素谱是我们研究夸克禁闭和检验不同夸克模型有效性的重要场所；同时，还可以通过研究粲偶素谱寻找超出标准模型以外的新物理[1]。粲偶素家族的最低束缚态ηc，一直是人们研究的热点，特别是它的强衰变模式被认为是研究量子色动力学的有效场所，高精度测量ηc衰变到矢量介子的过程，对我们进一步研究粲偶素模型具有重要的意义。人们对ηc及其强衰变的研究将近40年[2-3]，但是，到目前为止，仍然有大约30%的衰变模式尚未被发现，而且已经公布的分支比的精度也比较低，如，ηc→φφ的分支比的误差为11.36%[4]。文献[5-6]指出，由于ηc衰变到φφ信号比较明显，建议通过这个衰变道来测量ηc的自旋和宇称。本文将通过单举和遍举的蒙特卡罗样本对衰变道J/ψ→γηc→γφφ进行研究，其中φ介子通过K+K-重建。

1 第三代北京谱仪及其离线软件系统

第三代北京谱仪(BES III)是工作在第二代北京正负电子对撞机(BEPC II)上的一个大型多功能磁谱仪。BES III采用一系列先进的设计、技术和工艺，其各项设计指标均达到设计要求，并处于国际同类装置的先进水平。安装在BES III上的探测器自内而外由以下4个子探测器组成：主漂移室(MDC)、飞行时间计数器(TOF)、电磁量能器(EMC)和μ子探测器(MUC)。其中，MDC主要用于测量带电粒子的位置、动量以及电离能损等信息；在1 T的磁场强度下，动量为1 GeV/c的带电粒子的动量分辨能达到0.5%。TOF主要用来测量带电粒子在主漂移室内的飞行时间，并结合主漂移室测量的粒子动量和电离能损信息，进行带电粒子的种类鉴别；TOF的桶部和端盖的时间分辨率分别为80 ps和110 ps。EMC用于精确测量光子和电子沉积能量及其位置信息，同时提供中性能量的触发；在1 GeV的情况下，EMC的桶部和端盖的能量分辨率分别为2.5%和5%。MUC的功能主要是精确测量μ子的动量，同时为区别μ子和其他带电粒子(主要是π介子)提供信息，它的位置分辨率大概为2 cm[7]。

本文的研究依赖于BES III的离线软件系统(BOSS)。该系统利用Geant4对BES III探测器的几何结构，粒子在各个子探测器中的击中信息以及粒子在物质中的相互作用进行模拟。该系统通过KKMC产生子模拟e+e-湮灭得到粲偶素的过程，粲偶素的衰变过程则采用BesEvtGen进行模拟。为了对事例的选择条件进行优化，同时进行本底分析，本文将使用单举道和遍举道的蒙特卡罗样本进行研究。根据文献[4]的数值，通过BesEvtGen对单举道蒙特卡罗样本中已知分支比的衰变道进行模拟，未知的衰变道则使用Lundcharm进行模拟[8]。

2 J/ψ→γηc→γφφ→γ2(K+K-)的蒙特卡罗模拟

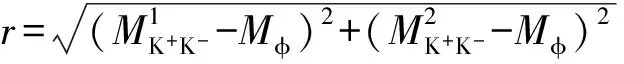
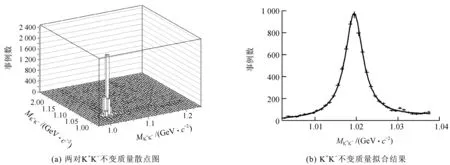
图1 K+K-不变质量散点图及其拟合结果Fig.1 Scatter plot of invariant mass of K+K- and fitting result of MK+K-

本文通过EMC的信息挑选光子，要求每个好光子必须同时满足如下3个条件：①和离它最近的带电径迹的夹角大于10°；②EMC里的时间在0到14个单位之间，每个单位为50 ns；③在桶部和端盖的沉积能量分别大于25 MeV和50 MeV。要求经过以上3个条件挑选出来的好光子数至少为1个。将这些光子逐一与4条带电径迹进行运动学拟合，即将它们总的4动量约束到质心系上，并挑选出使得运动学拟合具有最小χ2值的光子作为信号光子。通过对单举道蒙特卡罗的研究，本底主要包括3个部分(见表1)：①少一个光子的衰变道；②与信号道具有相同末态的衰变道；③多一个光子的衰变道。图2为不同蒙特卡罗样本的χ2比较，其中带误差的圆点表示单举道蒙特卡罗样本，黑色直方图表示信号道蒙特卡罗的分布，虚线表示本底蒙特卡罗样本的分布。由于单举道存在着本底，信号道蒙特卡罗样本的分布并不能很好地描述单举道样本，并且χ2值越大，两者的差别越大。但是，本底样本的分布与单举道样本在χ2值较大的部分在误差范围内是一致的，为了降低这些本底污染，要求χ2<80。

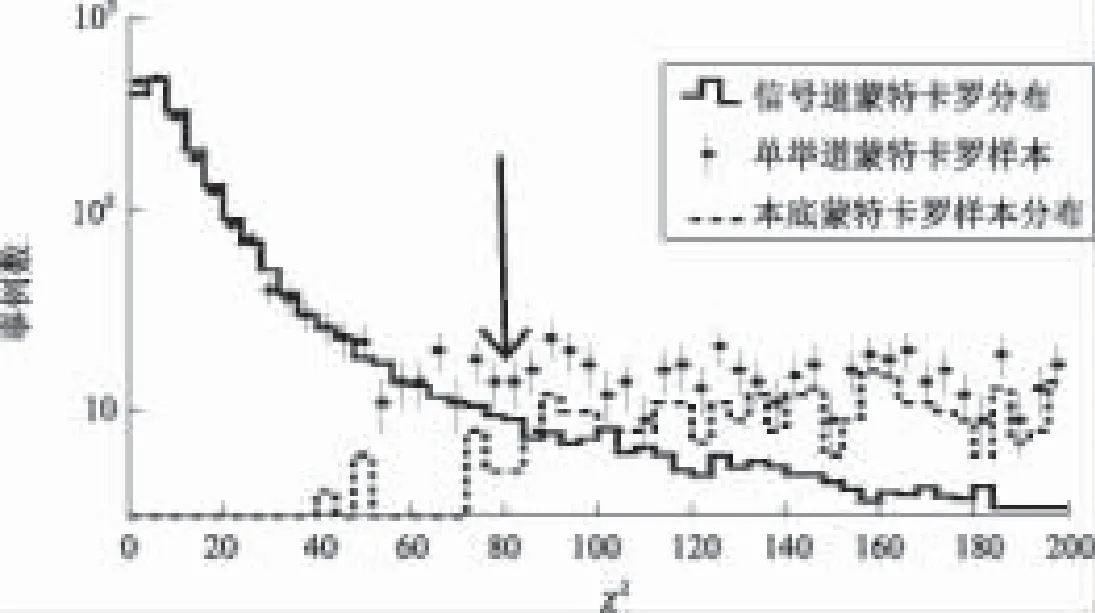
图2 单举道和遍举道蒙特卡罗样本的χ2分布Fig.2 The comparison of χ2 between inclusive and exclusive MC sample

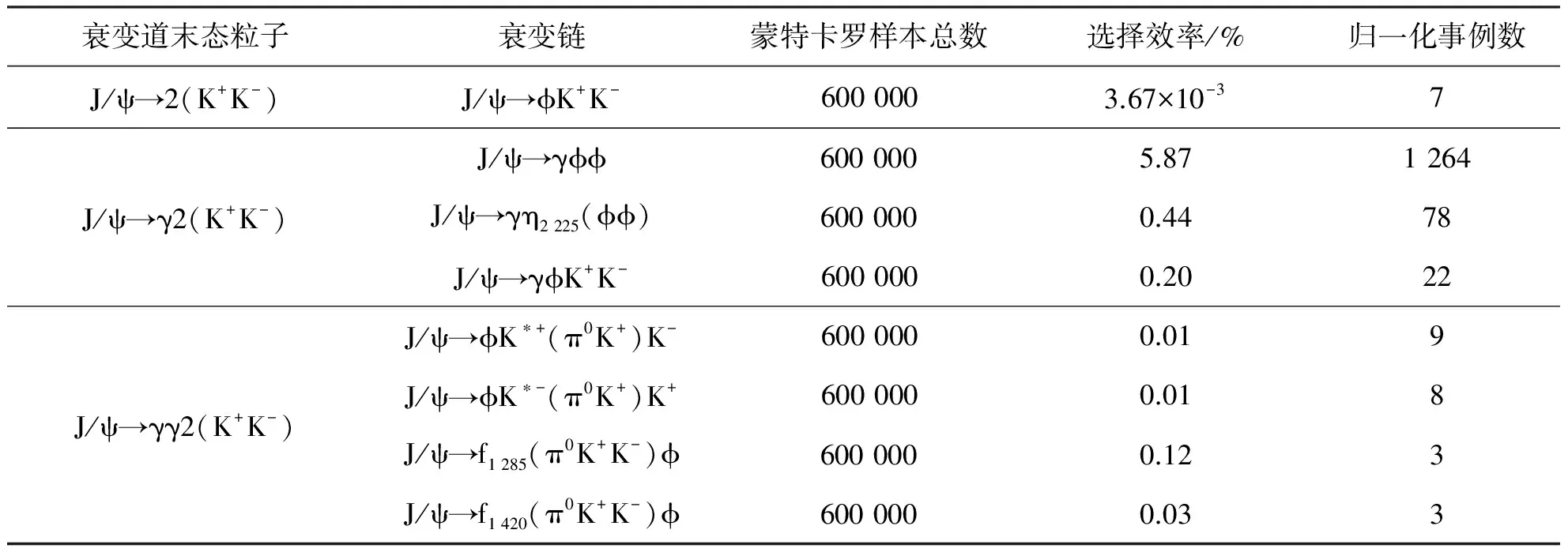
衰变道末态粒子衰变链蒙特卡罗样本总数选择效率/%归一化事例数J/ψ→2(K+K-)J/ψ→ϕK+K-6000003．67×10-37J/ψ→γ2(K+K-)J/ψ→γϕϕ6000005．871264J/ψ→γη2225(ϕϕ)6000000．4478J/ψ→γϕK+K-6000000．2022J/ψ→γγ2(K+K-)J/ψ→ϕK∗+(π0K+)K-6000000．019J/ψ→ϕK∗-(π0K+)K+6000000．018J/ψ→f1285(π0K+K-)ϕ6000000．123J/ψ→f1420(π0K+K-)ϕ6000000．033

3 ηc不变质量的拟合

本文将以上所有的条件应用于单举道蒙特卡罗样本，并对φφ的不变质量进行拟合，信号通过Breit-Wigner函数卷积高斯函数来描述，本底则使用二阶切比雪夫多项式来描述，如公式(1)所示。公式中m和σ分别表示ηc质量的中心值及其半高宽度，s描述的是探测器的分辨，a1和a2表示描述本底多项式的参数。

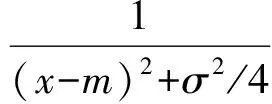
(1)

图3给出了φφ不变质量的拟合结果，图上的纵轴表示事例数，横轴表示φφ不变质量，带误差棒的点表示蒙特卡罗的分布，实线表示拟合结果，不带误差棒的的点表示本底形状，虚线表示信号的形状。拟合得到ηc→φφ的事例数N观察=472±49。利用公式(2)，可以得到ηc→φφ的分支比Br=(2.92±0.30)×10-3，单举道蒙特卡罗样本的输入值为2.7×10-3。本方案的结果在1倍标准偏差内和输入值是一致的。

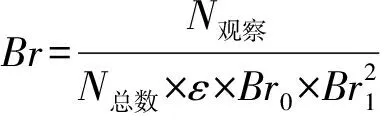
(2)

式(2)中单举道蒙特卡罗样本的总事例数N总数=2.25×108，事例选择的效率ε=22.88%，J/ψ→γηc的分支比Br0=1.30%，φ→K+K-的分支比Br1=49.10%。

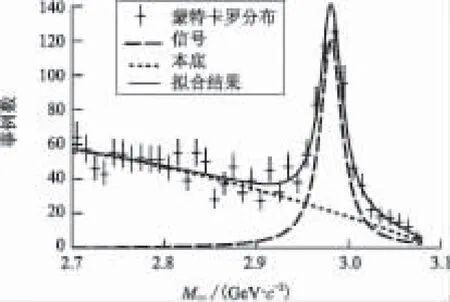
图3 φφ不变质量拟合结果Fig.3 Fitting result of the invariant mass of φφ

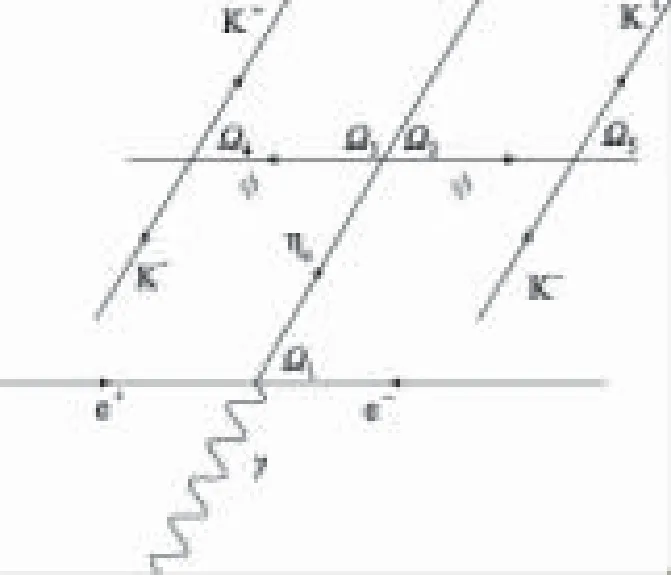
图4 J/ψ→γηc→γφφ→γ2(K+K-)螺旋度坐标系Fig.4 The helicity frame of J/ψ→γηc→γφφ→γ2(K+K-)

4 螺旋度角分布

4.1 螺旋度坐标系

本文参考文献[9]的方法来描述级联衰变J/ψ→γηc→γφφ→γ2(K+K-)的螺旋度坐标系，如图4所示。

1)J/ψ→γηc

2)ηc→φφ

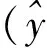
3)φ→K+K-

Ω4(θ4,φ4)和Ω5(θ5,φ5)定义为两个K+介子分别在其母粒子φ质心系下的立体角。

4.2 螺旋度角分布

对于任意一个两体衰变的衰变振幅具有如下的形式：

(3)

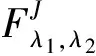
(4)

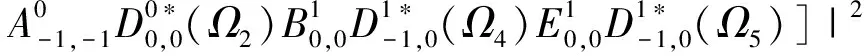
(5)

其中λ1=±1。对公式(5)积分可以得到各级衰变的角分布。

第一级衰变，J/ψ→γηc：

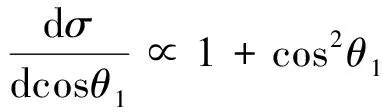
(6)

第二级衰变，ηc→φφ：因为初态粒子ηc的自旋为零，所以两个末态粒子φ在母粒子质心系下的角分布是均匀的。

第三级衰变，φ→K+K-：

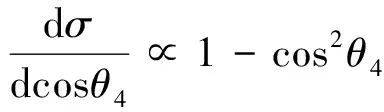
(7)

我们通过公式f(cosθ)=1+acos2θ对遍举道的光子和K介子的角分布进行拟合，拟合结果见图5。图中纵坐标表示事例数，横坐标表示该粒子在其母粒子质心系下的角度的余弦值，其中光子γ和K介子的拟合参数分别为aγ=1.024±0.050和aK=-0.997±0.004。在误差范围内，我们利用BESIII上离线软件系统产生的遍举蒙特卡罗样本与理论预期值一致。

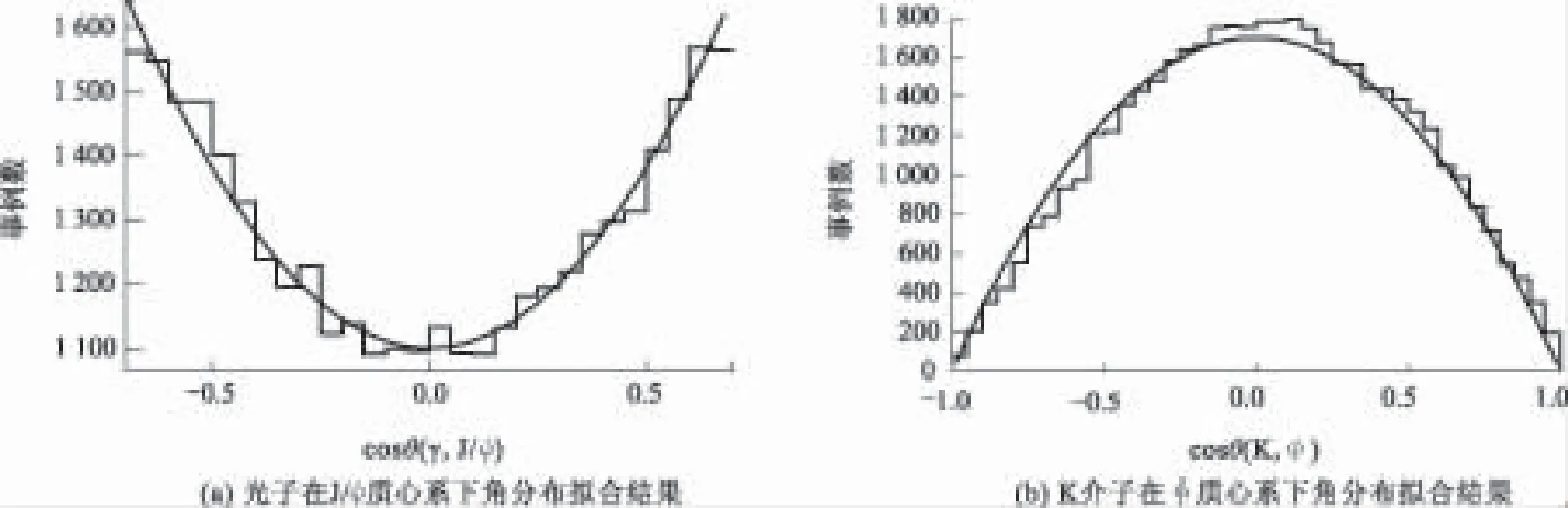
图5 光子和K介子的螺旋度角分布拟合结果Fig.5 The fitting result of photon’s and Kaon’s helicity angular distributions

5 结语

无论是带电粒子的动量分辨，还是光子的能量分辨，升级之后的BESIII均有了显著的改进。本文对J/ψ→γηc→γφφ→γ2(K+K-)衰变链进行研究，通过对比单举道和遍举道的蒙特卡罗样本，得到对信号造成污染的主要本底道，并利用MDC、EMC和运动学拟合等信息挑选信号，最终的选择效率为22.88%；相比BESII，本文在BESIII上的挑选效率提高了1.5倍。目前BESIII上拥有1.31×109的J/ψ数据，根据本文的研究结果，预计可以得到2 144±26个ηc→φφ的事例，其中的误差仅考虑J/ψ数据误差带来的影响。另外，本文利用螺旋度的方法分析了光子和K介子的角分布情况，蒙特卡罗的结果与理论计算值在误差范围内互相吻合。本文为未来BESIII上对粲偶素衰变的研究提供了一种可参考的方法，对于我们进一步研究ηc及其粲偶素家族谱的性质具有非常重要的意义。

[2] PARTRIDGE R,PECK C,PORTER F,et al. Observation of anηccandidate state with mass 2978±9 MeV[J].Phys Rev Lett，1980，45(14):1150-1153. DOI:10.1103/PhysRevLett.45.1150.

[3] BALTRUSAITISR M,COFFMAN D,HAUSER J,et al. Hadronic decay of theηc(2980)[J].Phys Rev D,1986，33(3):629-638. DOI:10.1103/PhysRevD.33.629.

[4] OLIVE K A,AGASHE K,AMSLER C，et al. Review of particle physics[J].Chin Phys C,2014,38(9):090001. DOI:10.1088/ 1674-1137/38/9/090001.

[5] BALTRUSAITISR M,BECKER J J,BLAYLOCK G T,et al. Observation of the decayηc→φφand determination of theηcspin and parity[J].Phys Rev Lett,1984,52(24):2126-2129. DOI: 10.1103/PhysRevLett.52.2126.

[6] CHANG N P,NELSON C A.Yang’s parity test for the new spin-0 mesons[J].Phys Rev Lett,1978，40(25):1617-1619. DOI:10.1103/PhysRevLett.40.1617.

[7] ABLIKIM M,AN Z H,BAI J Z,et al. Design and construction of the BES III detector[J].Nucl Instrum Meth A,2010，614(3):345-399. DOI:10.1016/j.nima.2009.12.050.

[8] PING Ronggang. Event generators at BES III[J].Chin Phys C,2008,32(8):599-602. DOI:10.1088/1674-1137/32/8/001.

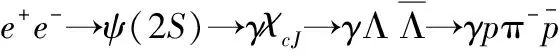
(责任编辑 黄 勇)

The Monte Carlo Simulation of J/ψ→γηc→γφφ at BES III

LIAO Guangrui，YANG Yongxu

(College of Physical Science and Technology，Guangxi Normal University，Guilin Guangxi 541004，China)

The Monte Carlo simulation of J/ψ→γηc→γφφ is performed at the BES III offline software system. The final states of the decay channel are selected by comparing the inclusive Monte Carlo with the exclusive Monte Carlo，and the efficiency is 1.5 times as that of BES II. The branching fraction of ηc→φφ obtained by this method is consistent with the input value of Monte Carlo within the statistical errors. 2 144±26 events number of ηc→φφ can be obtained when applying the procedure of the paper to the J/ψ data sample collected at BES III. A method of Helicity is used to calculate the angular distribution of all the particles in their mother frame，and the results are consistent with the fitting results of the exclusive Monte Carlo sample within the statistical errors. The result of this paper is meaningful for the high precision measurement of the channel and the data analysis at BES III experiment.

branching fraction；Monte Carlo simulation；helicity angular distribution

10.16088/j.issn.1001-6600.2016.03.001

2016-01-15

国家自然科学基金资助项目(11505034)；广西师范大学博士科研启动基金资助项目(17A4，17K)

杨永栩(1957—)，男，广西钟山人，广西师范大学教授。E-mail:yyxu@mailbox.gxnu.edu.cn

O572.21

A

1001-6600(2016)03-0001-06