利用遗传算法实现导航卫星星座优化设计

于 亮，张英利，朱 璇，张毓琴，谢 方

(1.西安测绘信息技术总站，陕西 西安 710054；2.国家测绘地理信息局 大地测量数据处理中心，陕西 西安 710054)



利用遗传算法实现导航卫星星座优化设计

于 亮1，张英利1，朱 璇1，张毓琴1，谢 方2

(1.西安测绘信息技术总站，陕西 西安 710054；2.国家测绘地理信息局 大地测量数据处理中心，陕西 西安 710054)

针对卫星星座设计中传统优化设计方法难以同时兼顾多种性能评价指标的问题，阐述了卫星星座的各项评价指标与星座设计的一般方法，并根据导航卫星星座的特殊要求给出了导航星座性能评价指标，提出了利用遗传算法求解区域导航星座参数的最优配置方法，最后仿照我国BDS系统的设计思路，利用STK平台进行了仿真计算。结果表明该方法能够为导航卫星星座性能优化设计提供借鉴。

导航星座；GPS；位置精度因子；遗传算法

0 引言

随着航天技术的飞速发展，利用卫星平台实现地球观测、导航和通信等功能日益成熟。这些功能的完成多借助多颗卫星共同发挥作用，完成特定功能的卫星就构成了卫星星座，例如地球观测卫星星座、卫星导航星座、通信卫星星座以及其他科学探测卫星星座等[1-4]。

卫星星座设计是一个十分复杂的问题，受到许多因素的影响。传统的星座设计方法仅仅考虑了星座的地理覆盖性能，并没有考虑诸如系统成本、太空环境、在轨推进需要、位置保持、寿命终结和处理等影响因素；再加上项目管理者、系统工程师和星座设计者经常会对同一个因素给予不同的重视程度：因此同样的任务需求给予不同的设计者往往会得到差异巨大的卫星星座设计[5]。

本文首先介绍了已有的几种常用星座模型以及遗传算法在星座设计中的应用，采用通用的6N星座模型(N为星座中的卫星数量)，将每颗卫星的6个轨道参数都作为星座模型参数，最大限度扩充了星座模型的参数空间。最后以区域导航星座的优化设计为例，利用星座位置精度衰减因子(position dilution of precision，PDOP)值作为优化目标函数，采用遗传算法求解最优的参数组合；并利用卫星仿真工具包(satellite tool kit，STK)仿真分析了该方法的可用性及优越性。

1 传统星座设计方法概述

1.1 星座设计的一般方法

单颗卫星的空间位置可采用6个轨道根数描述即(a,e,i,ω,Ω,M)。其中a为半长轴，e为偏心率，i为轨道倾角，ω为近地点幅角，Ω为升交点赤经，M为平近点角[5]，如图1所示。

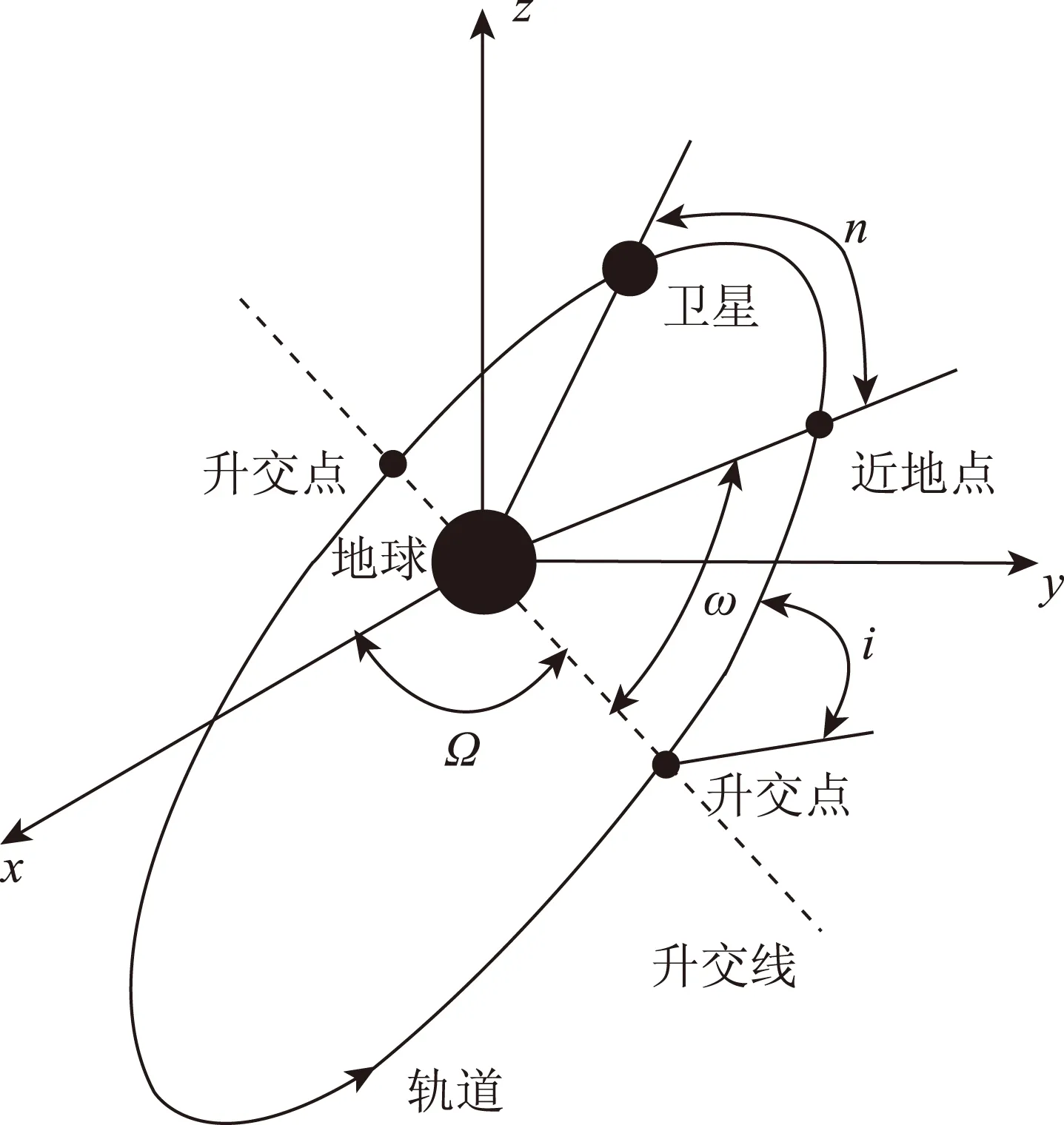
图1 卫星轨道根数

星座设计的一般思路可以总结为：以卫星轨道参数为主要关注点，以星座对地面的覆盖率作为优化目标。即在指定的轨道高度上，用最少的卫星或一定的卫星数量，使用最低的轨道，达到对地球表面(全球范围或某个纬度带)的覆盖要求。出于对称性及易于处理分析的考虑，一般使用均匀分布的圆型轨道。首先确定一定的星座构型，然后通过解析计算或基于梯度的优化方法得到满足全球或纬度带覆盖率要求的卫星数目最少的卫星星座设计。包括全球定位系统(global positioning system，GPS)在内的许多卫星星座设计都是使用该种思路。

对于功能要求越来越复杂的现代卫星星座而言，上述思路存在一些不足：首先星座构型的选择并没有一个公认的标准，对于相同的系统要求，没有统一的准则可以让不同的设计者做出确定的星座构型选择。其次目前很多星座开始面向区域覆盖，由单一轨道卫星组成的星座很难得到最优的地面覆盖，对于那些由混合轨道构成的新型星座，传统优化方法显得无能无力。再次现代卫星星座设计包含大量非传统优化准则，比如卫星失效后的星座可用性、平均/最大访问间隔时间、系统成本、几何精度衰减因子等，传统方法没有处理这些问题的能力。

1.2 通用的6N星座设计思想

针对上述传统星座设计思想存在的问题，本文采用一种通用的6N星座设计思想。

通用的星座参数模型适合于任何一种星座，模型中每颗卫星具有独立的参数：半长轴a0、倾角i0、偏心率e0、近地点幅角w0、升交点赤经Ω0和平近点角M0。这样对于一个由N颗卫星构成的通用星座，总共有6N个待优化参数。对于某些特定星座，模型中某些参数可能相同或者存在一定的数学关系。如Walker星座中的a0、i0、e0和w0均相等，同一轨道内卫星的Ω0也相同，卫星之间的Ω0和M0均受到T、P和F的约束。通用星座模型如图2所示。

图2 通用星座模型

从图2可以看出，设定的通用星座模型将卫星星座中每个卫星的6个轨道参数都作为待优化的设计参数。这种模型最大限度保证星座模型的通用性，避免由于特定星座模型的限制导致忽略某些潜在最优解。缺陷在于优化设计的参数显著增加，计算量也随之大量增加；但由于本文所采用的遗传算法(genetic algorithm，GA)本身就擅长处理参数众多的复杂问题，且可以通过改进GA及利用GA的并行性来提高计算效率：因此通用模型增加的优化设计参数不会对计算效率造成不利影响。

1.3 导航星座的构型设计

对于导航星座而言除了覆盖率指标外，还有其特殊要求，例如若某一时段卫星数量达不到4颗的基本要求则无法求解位置，若某一时段卫星的星下点过于集中，则导航定位方程将会出现严重的病态情况，系统服务也会终止；因此在利用通用模型时必需考虑这些特殊性要求。

本文仿照我国北斗卫星导航系统(BeiDou navigation satellite system，BDS)的设计思路，构建模拟的导航星座为由12颗卫星组成的混合星座，采用IGSO/GEO/MEO 3种不同轨道类型，其中：IGSO是指倾角不为0°的倾斜地球同步轨道(inclined geo-synchronous orbits)，其星下点轨迹是一个跨南北半球的“8”字，其交叉点在赤道上。这种轨道可对极地提供较好的覆盖，单颗IGSO卫星的覆盖性能可能不如1颗地球静止轨道(geostationary Earth orbit，GEO)卫星，但是利用多颗IGSO组成星座却可达到比GEO卫星更好的覆盖性能。

GEO卫星轨道是倾角为0°的地球同步轨道，相对于地面观测站，卫星在赤道上静止不动，其星下点轨迹是1个点。GEO卫星可提供大范围的地面覆盖，在其覆盖区域中任何一点，卫星均24 h可见；但其不能提供对极地的覆盖，发射费用较高，需要频繁的定点维持，且不利于精密定轨和精密星历的长期预报。

中圆地球轨道(medium Earth orbit，MEO)卫星的轨道高度一般在5 000 km以上，周期从上百小时到十几小时不等。其所受大气阻力可忽略不计，轨道相对稳定，便于精密定轨和精密星历预报，卫星对地面覆盖范围较大，可视时间长。目前GPS、格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)和未来的伽利略卫星导航系统(Galileo navigation satellite system，Galileo)等都选用了这种轨道。

星座具体参数构成为：5颗GEO卫星，包含5个设计参数，Ω1GEO，Ω2GEO，Ω3GEO，Ω4GEO，Ω5GEO。3颗IGSO卫星，第1颗IGSO卫星的平近点角、升交点赤经、轨道倾角为控制参数，由算法计算确定。3颗卫星平均分布在3个轨道面上，升交点赤经与平近点角相位均相差120°，轨道倾角相同，即包含3个设计参数iIGSO、ΩIGSO、MIGSO。4颗MEO卫星平均分布在2个轨道面上，轨道倾角、相邻轨道面上卫星的平近点角距差、长半轴、升交点赤经，以及第1颗MEO的平近点角由算法计算确定，即包含5个设计参数：aMEO、iMEO、ΩMEO、MMEO、ΔMMEO。

2 利用遗传算法进行优化设计

2.1 遗传算法简介

GA是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法[7]。其基本思想是基于达尔文的进化论，将问题的参数空间替代为编码空间，以适应度函数作为评价种群个体的依据，采用选择、交叉、变异一个基本操作建立其一个迭代过程，实现对自然选择和遗传机制的模拟。每一次迭代都是一个进化过程，通过该迭代得到的子代个体总是源于其父代个体；因此经过一定代数的进化，经过算法优化得到的种群个体就可能逼近于实际的最优解，从而达到求解最优参数的目的。

遗传算法工作流程如图3所示，其主要核心是计算适应度函数，以及选择、交叉、变异等遗传操作。

遗传算法在理论上是收敛的，能够得到全局最优解；但是由于其编码精度和迭代次数等的限制，往往收敛得到的解与真正意义上的全局最优解还有一定的差距。可以在计算能力允许的情况下，通过对遗传算法控制参数的合理设置使得计算结果尽可能接近全局最优解。

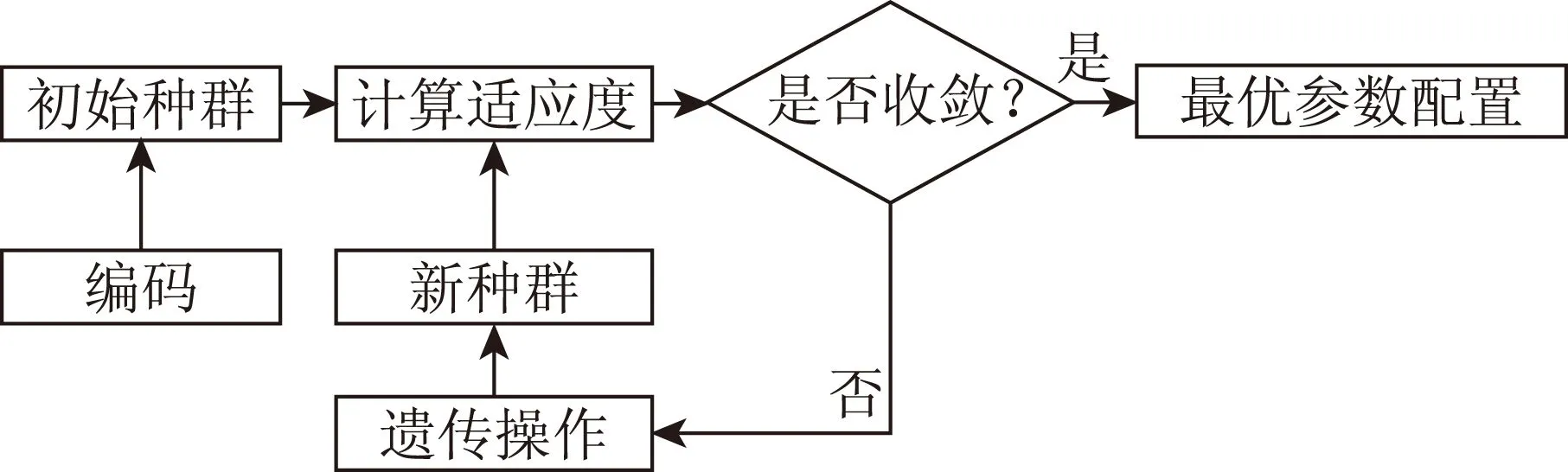
图3 遗传算法计算流程

对于卫星导航星座来说，其轨道参数具有不连续性及不可微，并且卫星星座任务目标性能受到许多因素影响，系统设计约束复杂且优化目标众多。传统方法所面临的这些困难恰好是GA的长处所在，GA搜索不依赖梯度信息，也不需要初值，算法中需要预先确定适应度评估函数的表达式，对该函数的唯一要求是可计算出能加以比较的非负结果。

由上文分析可知，仿真导航星座共有13个待优化参数。将遗传算法应用于星座优化，采用二进制方式对待优化参数进行编码，种群中每个体表示1个星座构型，将所有控制参数的二进制子串连接组成1个完整的染色体。如图4所示，在此基础上，通过选择、交叉、变异等遗传操作产生新的个体。按照图3所示流程进行优化处理，其中个体的适应度评估函数就是星座对目标区域的PDOP值。

图4 星座参数的二进制表达

2.2 单点PDOP值的计算

在导航星座的设计中需要考虑的评价指标一般包括共视卫星数目、卫星仰角、星座精度因子、导航精度、系统服务完整性等[8]。这些参数中绝大多数都与卫星星座的几何构型有关，且各个构型参数之间存在着固定的数学关系；因此在本文选取PDOP值作为星座性能指标的评判标准，它反映了星座几何分布对定位精度的影响。

PDOP值的计算如下：

在用户本地坐标系(x轴指向东，y轴指向北，z轴指向天顶)中，一个具有N颗卫星的星座中每颗卫星的位置可表示为

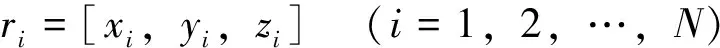
(1)

假设用户位置为(X0,Y0,Z0)，计算卫星的高度角α，若满足条件N(α≥0)≥4则此时相应的系数矩阵A为

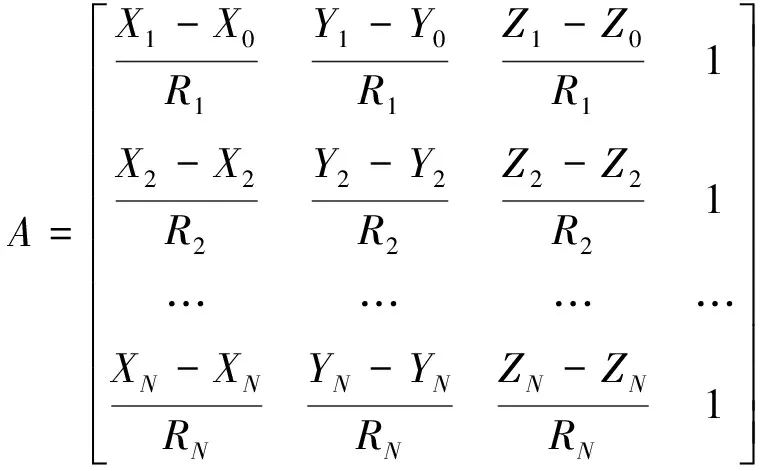
(2)

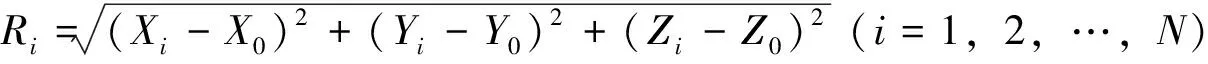
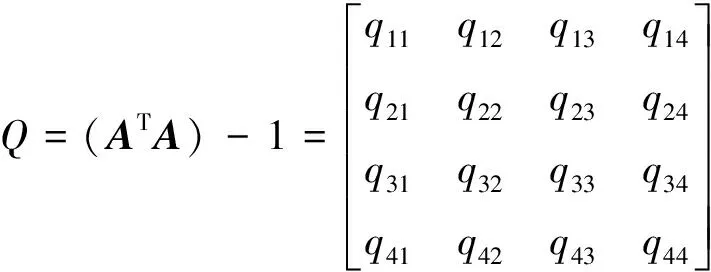
(3)

则最终用户位置的PDOP值为

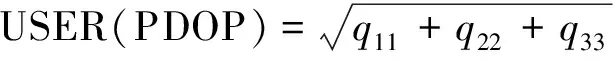
(4)

2.3 目标函数的建立

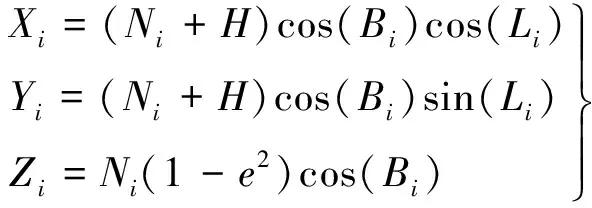
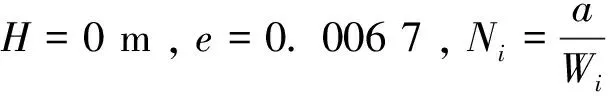
(5)

其物理意义为所有网格计算出的PDOP值的叠加值。考虑覆盖性指标的要求，应该保证所有网格尽量满足可见卫星数不少于4颗。同时为了提高函数的收敛性，将卫星数少于4颗的区域的PDOP设为1个较大的值即PDOPij(N<4)=999。

3 仿真与结果分析

3.1 优化设计结果

如上文分析区域卫星导航星座的待优化参数共有13个，且以星座PDOP值为目标函数。本文中遗传算法控制参数的取值为：每一代种群个体数目M=40；代沟G=0.9，采用二进制编码，编码长度为L=9；采用单点交叉的方式，交叉概率Pc=0.7，变异概率Pm=0.002，终止代数T=200。

遗传算法最终优化计算的结果见表1。

表 1 采用遗传算法最终优化设计结果

遗传算法寻找星座构型参数最优值的迭代过程如图5所示。

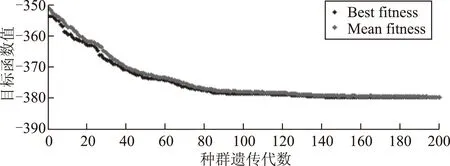
图5 遗传算法迭代求解星座构型参数最优值

图5中横坐标轴表示种群遗传代数；纵坐标轴表示目标函数值。从图中可以看出：遗传代数在120代左右时计算结果已经趋近最优值；这说明之前的参数设置中将终止代数设为T=200是合适的，兼顾了计算效率与准确性。

3.2 STK仿真分析

STK由美国AGI公司开发，可较方便地分析复杂的陆海空天任务，并能够提供易于理解的图表和文本形式的分析结果、确定最佳解决方案、产生位置和姿态数据、获取时间遥感器覆盖分析等[10]。本文采用STK对仿真的导航星座性能进行评估，在中国境内选取有代表性的5个地面观测站，分别为哈尔滨、青岛、喀什、三亚和西安，这5个站的概略坐标见表2。

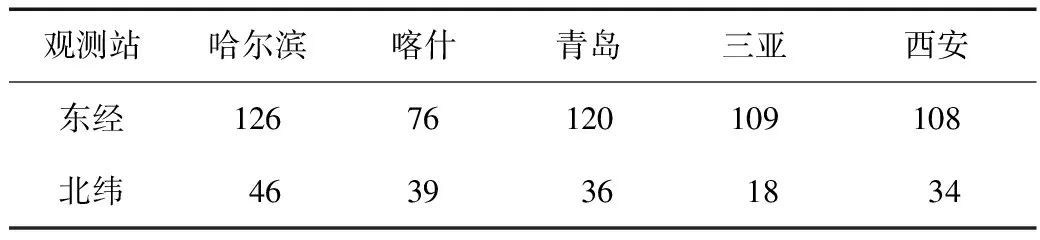
表2 国内5个观测站的分布情况 (°)

利用STK的Coverage Definition和Figure of Merit模块对星座的PDOP值进行分析，并取观测时间为24 h，得到该仿真星座某一时刻的PDOP值结果如图6所示。

图6 区域卫星导航系统的PDOP值分布

经统计分析可知各测站的可见卫星数目及PDOP值，如表3所示。

表3 各测站卫星数目及PDOP值大小

由表3可知，该星座在5个观测站均满足PDOP≤6，且可见卫星数不少于6颗，喀什站PDOP值变化较大且接近6，三亚站值最小且变化平稳。可见该星座基本能满足我国卫星导航的要求，西部性能稍差，东部地区可用性较高。

从以上结果可看出，本文采用遗传算法可以设计出具有一定实用价值的导航星座系统。当然本文所设计的导航星座系统的性能和GPS系统相比还有相当的差距，但通过改进目标函数的描述和优化计算法方法有望取得更好的设计结果。

4 结束语

本文介绍了导航星座性能评估的指标；研究了利用遗传算法设计区域导航星座的方法，以星座中每颗卫星的轨道根数作为待优化计算参数，通过卫星之间存在的数学关系对参数进行简化；最后对控制参数进行二进制编码，以星座PDOP值为目标函数，利用遗传算法对星座的设计参数进行优化。

本文最后采用该种方法仿照BDS设计了一个虚拟的区域导航星座，通过STK仿真分析，表明该方法设计的导航星座基本可以满足提出的预定要求。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010，39(1)：1-6.

[2] 宋丹，许承东，胡春生，等.基于遗传算法的多星座选星方法[J].宇航学报，2015，36(3)，300-308.

[3] 毛悦.导航卫星系统星座设计及性能分析[D].郑州：信息工程大学，2006：12-17.

[4] 郁聪冲，边少锋.现阶段北斗卫星导航系统可用性分析[J].海洋测绘，2012，32(5)：74-76.

[5] 曾喻江.基于遗传算法的卫星星座设计[D].武汉：华中科技大学，2007：35-39.

[6] 刘林，胡松杰，王歆.航天动力学引论[M].南京：南京大学出版社，2006：175-189.

[7] 王鲁.基于遗传算法的多目标优化算法研究[D].武汉：武汉理工大学，2009：73-79.

[8] 郭斐，张小红，于兴旺，等.基于STK软件的GALILEO系统仿真与分析[J].测绘信息与工程，2009，34(1)：3-6.

[9] 韩雪峰，张海忠，郑广伟.区域卫星导航系统覆盖性能分析[J].测绘与空间地理信息，2014，37(3)：149-152.

[10]杨颖，王琦.STK在计算机仿真中的应用[M].北京：国防工业出版社，2013：104-123.

Constellation optimization design of navigation satellites based on GA

YU Liang1，ZHANG Yingli1，ZHU Xuan1，ZHANG Yuqin1，XIE Fang2

(1.Xi’an Division of Surveying and Mapping，Xi’an，Shanxi 710054，China；2.Geodetic Data Processing Centre，NASMG，Xi’an,Shanxi 710054，ShanxiChina)

Aiming at the problem that it is difficult for traditional optimization design methods to adapt to multiple performance evaluation indexes in the design of satellite constellation，the paper introduced the general methods for designing and optimizing the satellite constellation，and according to the special requirements of navigation constellation，gave the performance evaluation indexes，then put forward the optimal configuration methods that use genetic algorithm to calculate the regional navigation constellation parameters，finally used the STK platform to simulate the calculation by design thought of BDS.Result showed that the proposed method could provide a reference for the constellation optimization design of navigation satellites.

navigation constellation；GPS；position dilution of precision (PDOP)；genetic algorithms

2016-03-04

于亮(1986—)，男，陕西咸阳人，硕士研究生，研究方向为高精度GNSS数据处理与卫星精密定轨工作。

于亮，张英利，朱璇，等.利用遗传算法实现导航卫星星座优化设计[J].导航定位学报，2016，4(4)：12-16.(YU Liang，ZHANG Yingli，ZHU Xuan，et al.Constellation optimization design of navigation satellites based on GA[J].Journal of Navigation and Positioning，2016，4(4)：12-16.)

10.16547/j.cnki.10-1096.20160403.

P228

A

2095-4999(2016)04-0012-05